Universal quantum operations and ancilla-based read-out for tweezer clocks

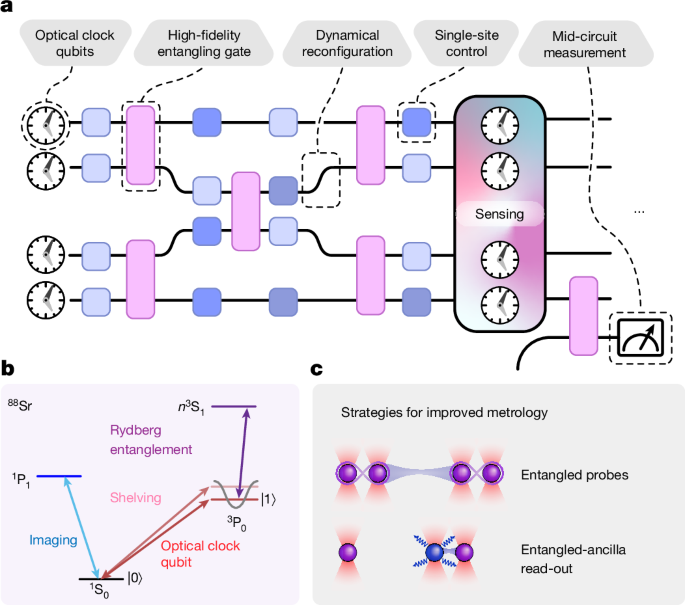
Experimental considerations and constraints

Our experimental set-up has been detailed in previous work^13,16,58. Here, we discuss the experimental requirements specific to executing quantum circuits on a quantum processor with optical clock qubits. In particular, several trade-offs need to be balanced in the choice of magnetic field, trap depth and interatomic spacing.

Due to laser frequency noise, high-fidelity single-qubit rotations benefit from a large Rabi frequency on the clock transition (¹S₀ ↔ ³P₀). The clock-transition Rabi frequency scales linearly with the magnetic field, and we achieved Ω = 2π × 2.1 kHz at 450 G. On the other hand, the Rydberg interaction strength varies with the magnetic field due to admixing with other Rydberg states⁶¹. Specifically, a numerical calculation (using the ‘Pairinteraction’ package⁶¹ and limiting the considered Rydberg states to n ± 5 for faster convergence) shows that the interaction energy peaked around 380 G and decreases for higher magnetic fields (Extended Data Fig. 1a). Our experimental measurements for several magnetic fields are consistent with this overall trend. Therefore, we operate at a magnetic field of 450 G, which provides a balance between a sufficiently high clock Rabi frequency and sufficiently strong Rydberg interactions.

Our nominal tweezer trap depth (U₀ ≈ 450 μK) is chosen to ensure efficient atom loading and high-survival, high-fidelity imaging⁶², as well as efficient driving of the carrier transition for clock qubits. However, we find that the Rydberg gate performs slightly better when the trap is turned off. In our case, this is predominantly due to beating between adjacent tweezers, which results in trap-depth fluctuations at a frequency of 650 kHz (equal to the tone separation on our tweezer-creating acousto-optic deflector). As the Rydberg transition (³P₀ ↔ 61³S₁) is not under magic trap conditions, this results in detuning noise for the gate operation. For an optimized CZ gate with traps kept on at 0.2U₀, we find that the two-qubit gate fidelity is lower by approximately 3 × 10^−3 (not shown). By placing an acousto-optic modulator in the tweezer optical path, we implement a fast switch-off of the trapping light (rise/fall time of the order of 50 ns). At this timescale, we find that switching traps off from a shallower trap 0.2U₀ is preferable as this imparts minimal heating with no observed loss for clock qubits. Furthermore, in MCR, efficient motional shelving relies on strong sideband coupling⁴⁴, which becomes stronger as the Lamb–Dicke factor increases (trap depth decreases). On the other hand, array reconfiguration benefits from sufficiently deep traps.

The experimental sequence, thus, involves adiabatic ramps of trap depth as well as fast switch-off and -on. After loading the atoms into the tweezers at U₀, we lower the tweezer depth to 0.5U₀ to perform erasure-cooling⁴⁴. For gate operations, we drive coherent clock rotations at 0.2U₀ and switch the trap off for about 500 ns to perform the Rydberg entangling pulse. When selective local MCR is applied, we adiabatically ramp to deeper traps of U₀ for the ancilla qubits, while holding the clock qubits at fixed depth.

We now discuss how we perform the dynamical array reconfiguration, shown in Fig. 1 as part of a full quantum operation toolbox. We coherently transport an atom across several sites by performing a minimal-jerk trajectory that follows x(t) = 6t⁵ − 15t⁴ + 10t³ for t ∈ [0, 1]. For this trajectory, the acceleration is zero at the two end points, which avoids the sudden jump in the acceleration profile and minimizes the associated jerk. The aim is to achieve minimal heating, which is especially important for driving optical clock transitions in the sideband-resolved regime.

With this trajectory, we find no significant temperature increase for atoms transported over four sites (equivalent to 13.26 μm) in 160 μs at trap depth U₀ (Extended Data Fig. 1b). This is the typical distance applied in dynamical array reconfiguration. Another interatomic spacing choice is 13.26 μm ≈ 19 × 698 nm (corresponding to the clock-transition wavelength), which would ensure an effective zero displacement-induced phase shift¹⁶.

Single-qubit (clock) error model

We characterize our ability to perform coherent single-qubit rotations with a global addressing beam and test our error model by driving the clock transition on atoms with an average motional occupation of \(\bar{n}\approx 0.01\), following erasure-cooling along the optical axis⁴⁴. We drive Rabi oscillations with a nominal Rabi frequency Ω = 2.1 kHz and observe 52.2(8) coherent cycles (Extended Data Fig. 2a). Applying a train of π/2 pulses along the X axis, we find a per-pulse fidelity of 0.9988(2). Note that in such sequences, the effect of slow frequency variations is suppressed. We, thus, characterize the π/2 pulse fidelity by applying a pulse train of π/2 pulses with random rotation axes ±X and ±Y (ref. ⁶³). The resulting π/2 pulse fidelity is measured to be 0.9978(4) (Extended Data Fig. 2c).

The dominant error source in the single-qubit operation is laser frequency noise, which is characterized by the frequency power spectral density (PSD) function S_ν(f). We characterize this with Ramsey and spin-lock⁶⁴ sequences.

Ramsey sequence

The Ramsey sequence is sensitive to the low-frequency component of the laser frequency PSD up to the inverse of the Ramsey interrogation time (approximately 100 Hz). In our experimental set-up, we observe day-to-day fluctuations in the Ramsey coherence time (Extended Data Fig. 2d). We use an effective model of the PSD at low frequencies (Extended Data Fig. 2f) to account for the fluctuations of the Ramsey coherence time. We set the PSD to be a constant H at low frequencies up to some frequency of interest (approximately 200 Hz) and find numerically that the Ramsey coherence time was inversely proportional to H.

Spin lock

To probe and quantify fast frequency noise up to our Rabi frequency, we perform a spin-lock sequence. We initialize all atoms in an eigenstate of \(\widehat{X}\) and turn on a continuous drive along the X axis for a variable time. Then we apply a π/2 pulse along the Y axis, which transfers all atoms into state \(| 1\rangle \) in the absence of errors. The probability of returning to \(| 1\rangle \) decays over time (Extended Data Fig. 2e), and the decay rate is predominantly sensitive to frequency noise at this Rabi frequency⁶⁴. By varying the Rabi frequency of the continuous drive field and measuring the decay of the probability in \(| 1\rangle \), we determine the frequency PSD by using the linear relation between the decay rate and the frequency PSD S_ν(f) at the Rabi frequency (Extended Data Fig. 2f).

To account for both the fast frequency noise measured by the spin-lock experiment and the slow frequency noise that determines the Ramsey coherence time, we interpolate the laser frequency PSD with a power-law function \({S}_{\nu }(f)={h}_{0}+{({h}_{\alpha }/f)}^{\alpha }\) upper-bounded by H at low frequencies. The model parameters h₀, h_α and α are obtained by fitting the spin-lock data (Extended Data Fig. 2e,f). The upper bound H is flexible within a range (shown as the shaded area in Extended Data Fig. 2f) and can effectively describe the day-to-day fluctuations of the Ramsey coherence time. This range is reflected in the uncertainties of the error model predictions quoted throughout this work.

In addition to laser frequency noise, note that although the single-qubit operations are sensitive to the finite temperature, we perform erasure-cooling⁴⁴ to prepare atoms close to their motional ground state (\(\bar{n}\approx 0.01\)). This has a negligible impact (approximately 1 × 10^−4) on the clock π/2 pulse fidelity, as predicted by our error model.

In addition to the error sources described above, we also include laser intensity noise, pulse shape imperfection, spatial Rabi frequency inhomogeneity and Raman scattering induced by the tweezer light. All these error sources result in an aggregate of approximately 1 × 10^−4 infidelity for the clock π/2 pulse.

With all described error sources included, the error model predicts an average π/2 fidelity of 0.9981(8) (Extended Data Fig. 2c), which is in good agreement with the experimental value of 0.9978(4).

Two-qubit gate fidelity benchmarking

Here, we give more details about the randomized circuit (Fig. 2), which is used to benchmark the CZ gate fidelity. We first apply a randomized circuit like the one proposed and used in ref. ¹⁷, which includes echo pulses (π pulses along X) interleaved with random single-qubit rotations and CZ gates (Extended Data Fig. 3a). For this circuit, we observe that both two-qubit (Rydberg) errors and single-qubit (clock) errors contribute to the inferred infidelity (Extended Data Fig. 3b,c). That such a circuit is sensitive to single-qubit gate errors, although the number of single-qubit gates was kept fixed, is because the probability distribution of two-qubit states before each single-qubit gate changes as a function of the number of CZ gates applied. Note that as errors affect entangled states and non-entangled states differently, changing the probability distribution would result in a non-unity return probability, even if the fidelity of CZ gates were perfect, in the presence of single-qubit gate errors. In this context, the sequence used in Extended Data Fig. 6 of ref. ¹⁷ also showed sensitivity to single-qubit errors, as the probability distribution between entangled and non-entangled states was not fixed as a function of the number of CZ gates.

To mitigate this effect, we design a randomized circuit (Extended Data Fig. 3a) such that the probability of finding any one of the 12 two-qubit symmetric stabilizer states would be uniform, irrespective of the number of CZ gates, at each stage of the circuit⁴⁷. We term this circuit the symmetric stabilizer benchmarking (SSB) circuit. Specifically, the probabilities of finding an entangled or separable state are equal throughout the circuit.

Using an interleaved experimental comparison, we find a difference of about 3 × 10^−3 between benchmarking methods in the fidelity directly inferred from the slope of the return probability (Extended Data Fig. 3b). This difference stems from the higher sensitivity of the echo circuit benchmarking to single-qubit gate errors. This observation is in good agreement with a full error model that accounts for both clock and Rydberg excitation imperfections (Extended Data Fig. 3c). This model confirms that the fidelity inferred from the symmetric stabilizer benchmarking circuit is an accurate proxy of the gate fidelity averaged over all two-qubit symmetric stabilizer states. We confirm that this observation holds over a wide range of error rates by rescaling the strength of individual error sources in the numerical model (Extended Data Fig. 3c). These include incoherent and coherent errors. However, note that coherent errors or gate miscalibration of larger magnitude would result in an increased error in estimating the gate fidelity, which is a common issue across various benchmarking techniques. Also note that the gate fidelity averaged over all two-qubit symmetric stabilizer states is equal to the gate fidelity averaged over two-qubit symmetric input states. This can be seen because these symmetric stabilizer states form a quantum state two-design on the symmetric subspace⁴⁷.

Correcting for the false contribution from leakage errors

We read out the return probability for the randomized circuit benchmarking by pushing out ground-state atoms and pumping clock-state atoms to the ground state for imaging. As part of this optical pumping, any population in the ³P₂ state would be pumped and identified as bright, which is the clock-state population. We, thus, correct for leakage from the Rydberg state into the state ³P₂ identified as bright. We separately measure the decay into ³P₂ per gate by repeating the benchmarking sequence, which is followed by pushing out the atoms in the qubit subspace and repumping the ³P₂ state for imaging. At a Rydberg Rabi frequency of 5.4 MHz, the false contribution to the CZ fidelity is measured to be 1.8(4) × 10^−4 per gate, in good agreement with numerical predictions. The CZ fidelity quoted throughout this work has been corrected downwards for this effect.

Two-qubit gate (Rydberg) error model

Our model for the two-qubit gate accounting for Rydberg errors is based on previous modelling of errors during Rydberg entangling operations^58,65. We adapt it to model the dynamics of a three-level system with ground (\(| 0\rangle \)), clock (\(| 1\rangle \)), and Rydberg states (\(| r\rangle \)). Following the optimization of the gate parameters for a time-optimal pulse^17,18 in the error-free case (Extended Data Fig. 4a), we fix these parameters and simulated noisy dynamics with the Monte Carlo wavefunction approach. The model includes Rydberg laser intensity noise, Rydberg laser frequency noise, Rydberg decay (quantum jumps) and atomic motion. The predicted contribution of each error source to the CZ gate infidelity is shown in Extended Data Fig. 4c. For the analysis shown in Extended Data Fig. 3c, we repeat the numerical simulation several times and change the magnitude of one of the error model parameters in each run. For example, we rescale the overall magnitude of the noise PSD for frequency or intensity noise or the Rydberg decay rate.

Data-taking and analysis

Data-taking and clock laser feedback

Here, we discuss the general data-taking procedure for all experiments described in the main text. Typically, each experimental repetition takes approximately 1 s. To collect enough statistics, we perform the same sequence for from several hours up to several days (for the randomized circuit two-qubit gate characterization). However, on this timescale, the clock laser reference cavity experiences environmental fluctuations, resulting in clock laser frequency drifts from approximately 10 to approximately 100 Hz over a timescale of approximately 10 min.

We, thus, interleave data-taking with calibration and feedback runs^16,65. To measure the clock laser detuning from atomic resonance, we perform Rabi spectroscopy with the same nominal power and π pulse time as used in the experiment. The laser frequency is then shifted accordingly by an acousto-optic modulator. Such feedback is performed every 5–10 min, depending on the details of the experimental sequence. We reccord the applied laser frequency shifts, which can serve as an indicator of the clock laser stability during the experimental runs. To compare the stability from experiment to experiment, we take the standard deviation of the feedback values. In the main text, the gate benchmarking (Fig. 2a,b) and the simultaneous preparation of a cascade of GHZ states (Fig. 3) have feedback standard deviations of 73 and 68 Hz, respectively. During the data-taking of the optical-clock-transition Bell-state generation experiment (Fig. 2c,d), the feedback standard deviation is 203 Hz, significantly higher than other experiments. To ensure the consistency of clock laser conditions among all experiments, we select the Bell-state generation experimental runs with associated clock laser feedbacks of less than 100 Hz. After applying this cutoff, the standard deviation of the feedback frequencies is 67 Hz, comparable with the other experiments.

To study the effects of the short-term clock stability, we analyse the Bell-state parity experimental runs with associated clock feedback frequencies less than a certain cutoff. With the cutoff frequency increasing from 100 Hz (results are presented in Fig. 2d) to 400 Hz (all data included), the parity contrast shows a clear decreasing trend (Extended Data Fig. 6a). This is consistent with our Bell-pair generation fidelity being limited by clock laser phase noise.

In contrast, note that using the randomized symmetric stabilizer benchmarking circuit to characterize the CZ gate itself, our results are consistent run to run and day to day within our experimental error bars. This further attests to the largely reduced sensitivity of this sequence to single-qubit gate errors stemming from clock laser drift and clock laser phase noise.

Error bars and fitting

Error bars on individual data points throughout this work represent 68% confidence intervals for the standard error of the mean. If not visible, error bars are smaller than the markers. The randomized circuit return probability shown in Fig. 2b and the parity signal shown in Fig. 2d are fitted using the maximum-likelihood method⁵⁸ (see details in the next section). Error bars on fitted parameters represent one standard deviation. Fitting for all other experimental data is done using the weighted least squares method.

Data analysis of Bell-state fidelity

We analyse the results of the Bell-state experiments as in our previous work⁵⁸. We use a beta distribution to assess the underlying probabilities. For the parity signal shown in Fig. 2d, we fit the data with a sine function with four free parameters: offset, contrast, phase and frequency. We find that using the maximum-likelihood method while taking the underlying beta distribution of each data point into account is necessary, as the standard Gaussian fit typically overestimate the contrast by approximately 0.015. This is because the beta distribution deviates from a Gaussian distribution when the two-atom parity is close to ±1, which breaks the underlying assumption of a Gaussian fit. From this, we obtain a parity contrast of \(0.96{3}_{-10}^{+7}\) (\(0.98{3}_{-10}^{+7}\) SPAM corrected). Together with the measured population overlap P₀₀ + P₁₁ = \(0.98{8}_{-7}^{+5}\) (\(0.99{4}_{-7}^{+5}\) SPAM corrected) (not shown), we obtain a Bell-state generation fidelity of \(0.97{6}_{-6}^{+4}\) (\(0.98{9}_{-6}^{+4}\) SPAM corrected). These results are obtained by analysing experimental runs with associated clock feedback frequencies of less than 100 Hz.

SPAM correction

The dominant measurement error stems from the long tails in a typical fluorescence imaging scheme. In our experiment, we infer the imaging true negative and true positive rates as F₀ = 0.99997 and F₁ = 0.99995, respectively, from experimental measurements through a model-free calculation (ref. ⁶⁶, section 2.6.7). Note that these are not state detection fidelities in a circuit, as state detection in a circuit would require a further push-out before imaging⁶². The probability of successfully expelling the ground-state atom from the trap for state discrimination is B = 0.9989(1). Taking these into account, the single-atom measurement-corrected values \({P}_{0}^{{\rm{m}}}\) and \({P}_{1}^{{\rm{m}}}\) have the following relation with the raw values \({P}_{0}^{{\rm{r}}}\) and \({P}_{1}^{{\rm{r}}}\):

where \(A={[B({F}_{0}+{F}_{1}-1)]}^{-1}=1.0012\) and \(C=1-{F}_{1}{[B({F}_{0}+{F}_{1}-1)]}^{-1}=-0.0011\). By assuming that a measurement was independent among the atoms, we extend this correction to multi-qubit measurements by taking the Kronecker product of the above matrix.

After correcting the measurements, we then correct for state preparation errors for the Bell-pair generation circuit (Extended Data Fig. 8). At the circuit initialization (state preparation) stage, we implement an erasure-cooling scheme⁴⁴ and analysed the results conditioned on no erasure detected. We identify that the dominant imperfections in this state preparation stage are (1) atom loss (with probability ε_l = 0.0027 for a single atom) and (2) decay from \(| 1\rangle \) to \(| 0\rangle \) (with probability ε_d = 0.0037 for a single atom). We keep track of how all two-qubit initial states (\(| 11\rangle ,| 10\rangle ,| 01\rangle ,| 1,\,{\rm{lost}}\rangle ,| {\rm{lost}},1\rangle ,\) …) contribute to the population distribution and the coherence at the measurement stage.

For the population distribution, apart from the ideal initial state \(| 11\rangle \), we keep track of how the erroneous initial states evolve under a perfect circuit execution and contribute to the final population distribution (Extended Data Fig. 8). We correct the bit-string populations to the first order of ε_d and ε_l. Following the probability tree, we can write:

where the bit-string probabilities \({P}_{{\rm{b}}}^{{\rm{m}}}\) are measurement-corrected and \({P}_{{\rm{b}}}^{{\rm{c}}}\) (the SPAM-corrected population) are issued from perfect initial state preparation, inherent to the quantum circuit execution errors.

For the coherence measurement, we keep track of how the different erroneous initial states contribute to the observed parity contrast. The error channel with one lost atom (initial state being \(| 1,\,\text{lost}\rangle \) or \(| \text{lost},\,1\rangle \)) does not affect the contrast due to having a different oscillation frequency. On the other hand, if an atom has decayed to the ground state (\(| 01\rangle \) or \(| 10\rangle \)), its parity oscillation frequency remains the same but with a π phase shift and a contrast of 0.5. This contributes negatively to the observed parity contrast. Hence, the measured parity oscillation contrast C^m (after measurement correction), in terms of the SPAM-corrected contrast C^c, to the first order of error probabilities, is

Erasure conversion for motional qubit initialization

In the main text, there are several results where the analysis of a final image is conditioned on a preceding fast image that verified the state preparation (after erasure-cooling) or motional qubit initialization (after shelving). First, note that erasure-cooling is needed strictly only for the motional qubit initialization in mid-circuit measurements. Additionally, we find improved single-qubit (clock) gate fidelities following erasure-cooling, and this improvement becomes significant for shallow tweezers. In contrast, the improvement in CZ gate fidelity following erasure-cooling is insignificant. In the full error model, we find only a 2 × 10^−5 increase when cooling the radial degree of freedom to its motional ground state.

For experiments in which MCR is applied (Figs. 4 and 5), we report the results conditioned on not detecting atoms in the ground state after a shelving pulse⁴⁴. We provide the results here with no conditioning for completeness. For measurement-based Bell-state generation (Fig. 5d), without erasure excision, the contrast is 0.39(3), and the population overlap would be 0.64(2), yielding a raw Bell-state fidelity of 0.52(2). For ancilla-based \(\widehat{X}\) measurement (Fig. 4c), the contrast, conditioned on the ancilla result \(| 0\rangle \) (\(| 1\rangle \)), is 0.60(3) (0.45(3)).

We attribute the limited shelving fidelity mostly to the limited Rabi frequency on the sideband transition, compared with typical frequency variations of the addressing laser or the trap frequency. Further limitations may arise from the uniformity of the trap waists (and depths) of different tweezers across the array. These limitations can be overcome with a more stable clock laser or by employing more advanced pulse sequences designed to be insensitive to such inhomogeneities⁶⁷.

Effects of clock error on four-qubit GHZ-state preparation

As discussed in the main text, during the preparation of the four-qubit GHZ state, the entangled state is vulnerable to finite atomic temperature and clock laser noise. Entangled states dephase during the array reconfiguration time, which is considered idle time in the quantum circuit, due to laser frequency noise. To quantitatively study the effect of laser frequency noise, we perform the experiment with different idle times. We then measure the parity oscillation contrast and the population overlap of the four-qubit GHZ state and compared with our error model predictions, assuming perfect CZ gates (Extended Data Fig. 9). The experimental pulse sequence is shown in Extended Data Fig. 9a. We increase the total idle time from 280 to 840 μs per arm and observe a decrease in both the overlap of the GHZ-state population and the parity oscillation contrast (Extended Data Fig. 9c,e). We also observe similar trends in a numerical simulation with our error model, which assumes perfect CZ gates, a finite temperature of \(\bar{n}=0.24\) and the calibrated clock laser frequency PSD. With the actual reconfiguration time (280 μs), this error model predicts the parity oscillation contrast to be 0.66 and the state fidelity to be 0.75, consistent with our experimental realization (contrast being 0.68(3) and fidelity being 0.71(2)).

Error model with a 26-mHz clock laser system

The experimental results with the variable idle time show that the generation fidelity of four-qubit GHZ states is limited by the clock laser frequency noise. This motivates us to simulate this state generation circuit with our clock error model and the frequency PSD of a 26-mHz laser⁵³. Keeping a finite temperature of \(\bar{n}=0.24\) and assuming perfect CZ gates, we find a contrast of 0.79 and a fidelity of 0.84 (Extended Data Fig. 6b). With this reduced frequency noise, we find the four-qubit GHZ generation fidelity less sensitive to the idle time. For the simultaneous generation of a cascade of GHZ states, we find that the four-qubit GHZ fidelity is consistent with the shorter idle time sequence. Furthermore, with zero temperature (\(\bar{n}=0\)), the clock error model predicts near-unity state fidelity (over 0.999). In this low-temperature and 26-mHz clock laser scenario, the state fidelity is limited by the entangling gate fidelity. With the high-fidelity entangling gate demonstrated in this work, we estimate the generation fidelity of four-qubit GHZ states to be approximately 0.97. This improvement of the atomic temperature could readily be achieved by erasure-cooling⁴⁴ or other methods⁶⁸. Note that erasure-cooling is not applied during this particular experiment to speed up the data-taking on a four-atom register.

Projected metrological gain

We analyse the experimental fidelities required to obtain a metrological gain in phase estimation. The metrological gain g is defined as the ratio of posterior variances². If we consider the gain of a protocol with N entangled atoms over the interrogation of N uncorrelated atoms, it can be written as \(g={(\Delta {\phi }_{{\rm{UC}}})}^{2}/{(\Delta {\phi }_{{\rm{C}}})}^{2}\), where \({(\Delta {\phi }_{{\rm{C}}})}^{2}\) and \({(\Delta {\phi }_{{\rm{UC}}})}^{2}\) are the posterior variances for the entangled case and the uncorrelated case, respectively. For both cases, we assume a dual-quadrature read-out^5,16,51. We first describe the expected metrological gain with perfect state preparation and then consider the case of imperfect state preparation.

There are two distinct regimes for phase estimation. Local phase estimation corresponds to the limit of a vanishing prior phase width or equivalently to short interrogation times in atomic clocks. This limit holds only if the prior phase width is smaller than the dynamic range of the quantum state. In this limit, the optimal probe state is an N-atom GHZ state, and the gain is² g ≈ N.

For a large phase prior distribution width or equivalently for long interrogation times in atomic clocks, GHZ states do not provide a metrological gain due to their limited dynamic range, so that new protocols are needed. In the main text, we consider the protocol proposed in refs. ^1,4 and demonstrate a scheme to generate the required input state and read out the phase in both quadratures (Fig. 3). The protocol uses N atoms divided into M groups of GHZ states with K = 2^j atoms each, where j = 0, …, M − 1. The number of atoms in the largest GHZ state is, thus, \({K}_{\max }={2}^{M-1}.\) The projected metrological gain with ideal state preparation was predicted to be \(g\approx {{\rm{\pi }}}^{2}N/(64\log (N))\) (ref. ⁴). The gain can be understood by considering phase estimation at the Heisenberg limit for the largest GHZ state, which contained N/2 atoms. To exponentially suppress rounding errors in phase estimation, one needs to use n₀ copies of each GHZ state with \({n}_{0}=(16/{{\rm{\pi }}}^{2})\log ({\rm{N}})\). Note that these expressions hold only in the limit of large N.

We now consider a limited number of atoms N and analyse the effect of finite state preparation fidelity on the projected metrological gain. We assume that the interrogation time is long and perform numerical Bayesian phase estimation. We use a Gaussian prior distribution to model the prior knowledge of the laser phase. For Bayesian phase estimation, the posterior variance of a given protocol depends on the variance of the prior distribution. The figure of merit of phase estimation is typically given by^6,37 R = Δϕ_C/δϕ, where δϕ is the prior phase distribution width. R quantifies how much information was obtained in the measurement compared to our initial knowledge of the parameter. It has been shown numerically that for relevant values of N (N ≈ 100), the optimal performance, quantified by R, is obtained for a phase prior width around δϕ = 0.7 rad for a large class of states^6,37. We, therefore, choose to work with this prior width. Experimentally, the prior width is set by the Ramsey interrogation time and can be tuned to this optimal value.

Using the protocol in ref. ⁴ for GHZ states with one, two or four atoms, the minimal number of copies per GHZ size is n₀ = 6, resulting in N = 42 atoms (Extended Data Fig. 7). Using optimal Bayesian estimators³⁷, we find numerically a metrological gain of 1.627 (2.114 dB) with perfect state preparation. Imperfect preparation fidelity results in a parity signal with limited contrast C(K) for a K-atom GHZ state. The probabilities for the outcome of a parity measurement are then modified to \(P(\pm )=(1\pm C(K)\cos (K\phi ))/2\), where {+, âˆ’} denote even and odd parity, respectively.

To estimate the effect of such limited contrast on the metrological gain, we consider two characteristic scenarios, motivated by our experimental results. First, we look at a case with perfect state preparation for the one-atom and two-atom GHZ states (C(1) = C(2) = 1), whereas the four-atom GHZ state has a finite parity signal contrast C(4). In this case, we find numerically that the minimal contrast to obtain a gain g ≥ 1 is C(4) = 0.656. This is higher than the threshold contrast for a narrow prior width given the same state, that is \(C\ge 1/\sqrt{{K}_{\max }}=0.5\) (refs. ^2,52).

Second, we look at a case where the contrast of each GHZ state scales as \(C(K)={F}_{0}^{K}\), where F₀ is the effective fidelity per qubit. We repeat the calculation and find that the threshold fidelity to obtain a gain was F₀ = 0.969, or equivalently a contrast of C(4) = 0.969⁴ = 0.883 for the four-atom GHZ state. Numerically, this threshold seems to be robust to the introduction of more copies of the one-atom and two-atom GHZ states: if n₀ = 12 only for these states (keeping n₀ = 6 for the four-atom GHZ states), the threshold is only slightly reduced to F₀ ≳ 0.965. Finally, we show the projected metrological gain for various F₀ with respect to the number of atoms in the largest GHZ state used in the protocol of ref. ⁴ in Extended Data Fig. 7.

Our experimental values for C(K) from the simultaneous GHZ-state generation scheme (C(1) = 0.82, C(2) = 0.68 and C(4) = 0.52) fall between the two cases considered here: the best case scenario of C(K) = 1 for \(K < {K}_{\max }\) and the worst case scenario of \(C(K)={F}_{0}^{K}\). Hence, we expect the threshold for metrological gain to lie between the values obtained from these two cases.

Note that the observed parity oscillation contrasts in our current experimental demonstration are below these thresholds. However, the contrast reduction is entirely dominated by clock laser noise (Extended Data Fig. 6). With the high-fidelity CZ gates obtained in this work, where F_CZ ≈ 0.996, combined with a reduced clock laser noise (achieved, for example, by a laser with frequency PSD as in ref. ⁵³ as discussed above), we numerically project a performance superior to the same number of uncorrelated atoms. Specifically, if we assume F₀ ≈ 0.996, the predicted metrological gain with six copies of GHZ states with one, two or four atoms each is calculated to be 1.519 (1.815 dB). If eight-atom GHZ states are included, the predicted metrological gain with eight copies of GHZ states with one, two, four or eight atoms each is calculated to be 1.893 (2.772 dB). Note that the above gain analysis assumes zero dead time. Introducing dead time would degrade the gain, and we defer the analysis of this effect to future work.

Repeated ancilla detection with ancilla reuse

For the MCR illustrated in Fig. 4, fast 18 μs imaging⁵⁸ is applied with a fidelity of approximately 0.96 at a tweezer spacing of 3.3 μm. The strong driving on the ¹S₀ ↔ ¹P₁ transition without cooling results in the low survival of detected atoms. Therefore, for experiments where repeated ancilla measurements are needed, we refill the original ancilla position with another atom through array reconfiguration. Alternatively, we recool and reuse the ancilla atoms instead of refilling them. In this section, we describe a proof-of-concept experiment with different imaging parameters for the ancilla atoms (Extended Data Fig. 10).

The new imaging scheme is based on the standard high-fidelity, high-survival imaging with cooling light (¹S₀ ↔ ³P₁ intercombination line)⁶². We increase the imaging power to collect more photons over 10 ms and apply the cooling light on one of the axes for another 10 ms, which is shorter than the motional shelving coherence time  of approximately 100 ms (ref. ⁴⁴). This imaging scheme allows us to obtain an imaging fidelity of 0.98 with 0.965(2) survival (Extended Data Fig. 10a).

We then check whether we could coherently apply single-qubit rotations after this 10 ms imaging by applying a π/2 pulse and a second π/2 pulse with a variable phase (Extended Data Fig. 10b). The measured coherence after imaging 0.94(1) (Extended Data Fig. 10c) is mainly limited by survival, which could readily be improved with further optimizations on cooling during the imaging. Once added to the complete MCR (Extended Data Fig. 10d), we see a similar coherence for the detected atoms in the ground state (blue) and a slightly lower coherence for the undetected atoms in the clock state (red), due to the decay (time constant approximately 300 ms) during the 10 ms cooling. These decayed atoms contribute doubly to the loss of coherence of approximately 0.07. With this coherent driving, we can see when the ancilla atoms are ready to be reused. In the same experiment, we also measure a coherence of approximately 0.73 on the shelved atoms after unshelving them (not shown), matching the numbers for motional coherence in our previous work⁴⁴.

Weight-2 ancilla-based parity read-out

Here, we give the fitted parameters of the plot presented in Fig. 5b. For the direct read-out on the Bell pair, we fit an oscillation of 16.5(1) kHz with a phase 3.16(7) rad and a contrast of 0.77(3). The ancilla read-out gives a Ramsey oscillation of 16.5(2) kHz with a phase of 3.19(9) rad and a contrast of 0.59(4). In a separate experiment interleaved with this experiment, we measure the single-atom detuning to be 8.26(5) kHz.

With perfect gates, the quantum circuit in Fig. 5a yields an oscillating state between \(| {\varPhi }^{+}\rangle \otimes {| 0\rangle }_{{\rm{ancilla}}}\) and \(| {\varPhi }^{-}\rangle \otimes {| 1\rangle }_{{\rm{ancilla}}}\). For either state, the pair would be measured in \(| 00\rangle \) or \(| 11\rangle \) in this ideal case. Given this information, one can post-select on the experimental repetitions where the pair is measured in the expected state, either \(| 00\rangle \) or \(| 11\rangle \). This post-selection could identify errors in the execution of the circuit. Looking at the oscillating state, this post-selection should not bias either of the ancilla measurement outcomes. Performing this post-selection analysis (not shown), we see a Ramsey oscillation of 16.5(3) kHz and a contrast of 0.71(8).