Latent resistance mechanisms of steel truss bridges after critical failures

Specimen design

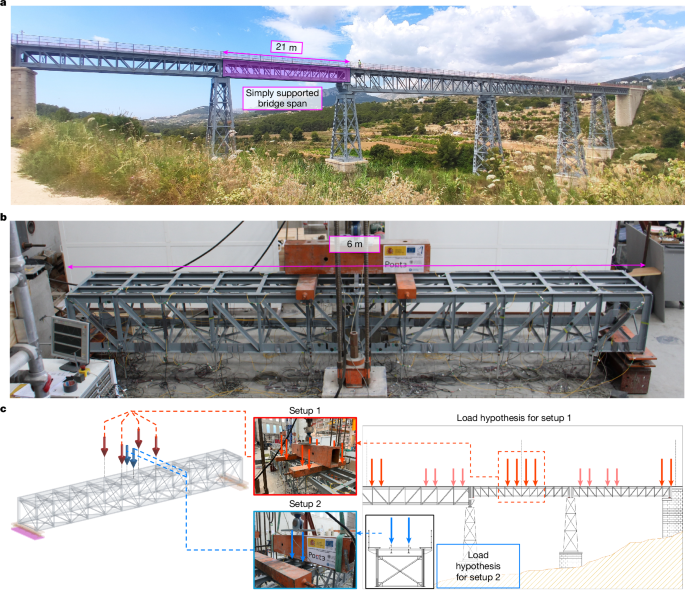
We performed experimental tests on a scaled specimen that reproduces one of the simply supported spans of a real railway bridge (Supplementary Video 1). The considered simply supported span (Extended Data Fig. 1) consists of two lateral Pratt trusses (the main system) connected by vertical transverse X-bracings, horizontal upper and lower X-bracings and lower transverse beams (the bracing system), as well as upper transversal floor beams with longitudinal rail beams (that is, stringers) joined to them (the floor system).

To accurately reproduce structural behaviour, load redistribution and modes of failure, we designed the scaled bridge specimen using the following scaling criteria based on dimensional analysis^38,39:

1. 1.

   The model is made of steel with a yield strength f_y = 275 MPa (S275 according to EN 10025-1:2004 (ref. ⁵¹)). The density and mechanical properties of the steel of the actual bridge are practically the same as the density and mechanical properties of S275 steel. Therefore, all scaling factors related to the material (density: λ_ρ, Young’s modulus: λ_E, Poisson’s ratio: λ_ν) are taken equal to one.

2. 2.

   A scale factor λ_L = 3.5 has been chosen for member lengths. Cross-section areas and moments of inertia have been scaled accordingly (\(\lambda _\rmA=\lambda _\rmL^2\), \(\lambda _\rmI=\lambda _\rmL^4\)) (Supplementary Information Section 1).

3. 3.

   Assuming that the scale of forces is λ_F, measured displacements of the model scale according to \(\lambda _\rmd=\lambda _\rmF\frac\lambda _\rmL\lambda _E\lambda _\rmA=\frac\lambda _\rmF\lambda _\rmL\) and measured rotations scale according to \(\lambda _\theta =\frac\lambda _\rmF\lambda _\rmL^2\).

4. 4.

   Internal forces (axial and shear) are scaled according to λ_N,V = λ_F and bending moments are scaled according to λ_M = λ_Fλ_L.

5. 5.

   Three similitude conditions are especially relevant for the selection of the scale factor for the external forces:

   1. a.

      Similitude of stress and yield strength: \(\lambda _\sigma =\frac\lambda _\rmF\lambda _\rmA=\lambda _f_\rmy=1\). This criterion leads to \(\lambda _\rmF=\lambda _\rmL^2\).

   2. b.

      Similitude of axial force and member buckling load: \(\lambda _\rmF=\frac\lambda _E\lambda _\rmI\lambda _\rmL^2=\lambda _\rmL^2\).

   3. c.

      Similitude of stress and local buckling stress. The critical local buckling stress is given by a relation of the type \(\sigma _\rmcr=k\rm\pi \fracEt^212(1-\nu ^2)b^2\), in which k is a buckling constant, E is Young’s modulus, ν is Poisson’s ratio, t is the section wall thickness and b is a representative wall length. Therefore, \(\lambda _\sigma =\frac\lambda _\rmF\lambda _\rmL^2=\frac\lambda _\rmE\lambda _t^2\lambda _(1-\nu ^2)\lambda _b^2=\frac\lambda _t^2\lambda _b^2\) and this criterion leads to \(\lambda _\rmF=\lambda _\rmL^2\frac\lambda _t^2\lambda _b^2\).

   We have selected a scaling factor \(\lambda _\rmF=\lambda _\rmL^2\) for the external forces. As well as reproducing the similitude of stresses, yield strength and axial forces, this choice ensures the similitude of member buckling loads; this is crucial, as member buckling determines the load redistribution in the tested specimen near the collapse.

6. 6.

   The selected scale factor for external forces is not applicable to the mass, because the latter scales with the volume (\(\lambda _\rho =\lambda _\rmL^3\)). To keep the ratio of vehicle load to self-weight of the scaled-down specimen as in the actual bridge and for the analysis of forces in the bridge, self-weight should be considered as an external load, with a scaling factor \(\lambda _\rmL^2\). This leads to a scaled self-weight load larger than the actual weight of the bridge specimen plus the dead load of the testing rig used for distributing the test loads. To take this into account, we have defined the total value of the test load so that it includes the correction of the self-weight. The experimental setup and the justification of the test load considering the self-weight correction are explained in the following section.

The scaled bridge design is shown in Extended Data Fig. 2 and the complete geometric properties of all cross-sections are provided in Supplementary Information Section 1 (together with comparisons between theoretical and actual scaled-down values). Riveted connections typically used in such steel truss bridges do not behave as the idealized pin joints assumed in design. Instead, they effectively perform as rigid connections and usually have a high capacity for resisting bending moments²⁸. As such, all joints of the scaled-down specimen were welded to ensure full-strength connections in a simplified manner.

On the basis of the selected scaling factors, the measured displacements scale in the same way as member lengths, λ_d = λ_L; rotations and load factors do not require scaling, λ_θ = λ_{Load factor} = 1; internal forces scale as the external ones, \(\lambda _\rmN,V=\lambda _\rmL^2\); and bending moments scale as \(\lambda _\rmM=\lambda _\rmL^3\). The results presented in this work can thus be easily scaled up by applying these conversions.

Experiment and monitoring design

After fabrication, the scaled-down bridge specimen had a self-weight of 4.2 kN. It was transported to the ICITECH laboratory and positioned to reproduce the same boundary conditions as those of the real bridge span, with a hinged support on one end and a rolling support on the other (Extended Data Fig. 2). Tests were carried out on the steel material according to EN ISO 6892-1 (ref. ⁵²) to characterize its stress–strain behaviour (Supplementary Information Section 1).

The load applied during tests corresponded to the operational loads of the reference bridge (Extended Data Fig. 3). The real bridge is loaded by actual convoys of two vehicles with two-axle bogies and a maximum nominal axle load of 88.4 kN. The loading setup used for testing corresponds to the convoy position that is most unfavourable for global bending of the bridge span. Specifically, this occurs when the heaviest bogies of each vehicle are centred with respect to mid-span (with four axles of 88.4 kN). For testing, these loads were applied using a hydraulic jack and distributed on the main system of the bridge through a testing rig with a weight of 5.4 kN. Loads of the same bogie were grouped together.

The load of the hydraulic jack was introduced pseudo-statically (at a displacement rate of 0.05 mm s⁻¹). The magnitude of this load results from multiplying the nominal load of the convoys by the following dynamic effects: (1) an estimated dynamic impact factor of 1.18 representing the dynamic effect of the vehicles passing through the bridge at a certain speed⁵³ and (2) a dynamic amplification factor of 1.9 owing to the sudden loss of structural members during the analysed damage scenarios^54,55. Consequently, the operational load for the bridge specimen was scaled as follows:

To (1) keep the ratio of operational load to self-weight of the scaled-down specimen as in the actual bridge and (2) correctly analyse forces in the bridge, self-weight should also be considered as an external load with a scaling factor \(\lambda _\rmL^2\). Considering that the actual self-weight of the real bridge span is 171 kN and that only the dynamic amplification factor owing to sudden loss of structural members (that is, 1.9) is applicable in this case, the scaled self-weight should be:

This leads to a scaled self-weight load that is larger than the actual weight of the bridge specimen (4.2 kN) plus the dead load (5.4 kN) of the testing rig used for distributing test loads. The total test load applied by the hydraulic jack was therefore corrected to account for this:

Before tests, it was also checked that the load was small enough to ensure that none of the components of the bridge would enter a nonlinear mechanical regime, thus preventing failure and damage of one test from affecting the next.

Up to nine different damage scenarios were considered through component removal (that is, by cutting main components), representing the failure of different member types at critical positions in which they support very high levels of internal load. The considered damage scenarios were: (1) a lower chord in the middle of the span; (2) one of the first diagonals of the span; (3) one of the second verticals of the span; (4) and (5) a horizontal and a vertical bracing located close to the load applied by the jack; and (6) a transversal beam. The fourth and fifth damage scenarios were performed in two testing phases representing the failure of one and two bracing elements of each damage scenario type. The sixth damage scenario was also performed in two phases representing partial and total loss of a transversal beam. For these damage scenarios that involve the failure of transversal beams, the load setup was changed because a transversal beam is most critically loaded when only one of the axles of a bogey is positioned directly on it (Extended Data Fig. 3). For these tests, the scaled operational load only considers the highest traffic load that can be transmitted through a single axle and corresponds to 16 kN. Because the dead load of the testing rig was 2 kN in this case and the self-weight of the entire bridge span is not involved in the structural response of the transversal beam, the total applied load by the hydraulic jack was 14 kN. The defined damage scenarios with the different load setups are shown in Extended Data Figs. 3 and 4. For each damage scenario, the bridge specimen was tested twice, once with the undamaged state and again after component removal. After finishing both tests for each damage scenario, the two parts of the cut component were welded together to retrofit the bridge to its original state before assessing the following damage scenario (Supplementary Information Section 1 and Supplementary Video 2). For the last damage scenario (involving the removal of a diagonal), as well as testing with the specified load of 80 kN, the applied loads were also increased until the system collapsed. This last test was used for the validation of the computational models presented in the final section of Methods.

To monitor the structural behaviour during tests, we heavily instrumented the bridge specimen with several sensors. A total of 80 strain gauges and 14 displacement transducers were placed at key locations in different parts of the bridge. The data from these sensors were complemented by pictures and videos of the structural response captured by three high-resolution cameras (Supplementary Information Section 1 and Extended Data Fig. 5).

Simulations for studying the onset of ALPs

We performed an extensive set of computational simulations to characterize how the structural response of the bridge changes after the failure of main components. Each failure was represented by removing a single component in the corresponding simulation. At this stage, our computational simulations are aimed at identifying and extracting the resistance mechanisms and the corresponding ALP patterns that the bridge can activate for several damage scenarios.

The kernel of the computational campaign is a three-dimensional finite element model of the undamaged scaled bridge subjected to the same conditions reproduced in tests. With this model, we performed 222 different simulations, each involving the removal of a main component. For each damage scenario simulation, we analysed joint displacements, support reactions and element internal forces at different points on the element cross-sections. The entire process (including modifying the base finite element model and post-processing results) was implemented using a MATLAB⁵⁶ code.

The finite element model of the scaled bridge was implemented in DIANA FEA software⁵⁷. The bridge was modelled using a total of 2,798 two-node, three-dimensional Timoshenko/Mindlin⁵⁷ (shear-deformable) beam elements with six degrees of freedom per node. Geometric and mechanical nonlinearities were considered. The former considers possible member and system instabilities, whereas the latter considers the nonlinear stress–strain characteristics of the material derived from tensile tests (Supplementary Information Section 1). We assumed⁵⁸ a Poisson’s ratio of 0.3 and a density of 7,850 kg m⁻³. Each structural member was discretized into at least five beam finite elements. All joints were modelled as rigid. The boundary conditions and load arrangement reproduce those of the experimental campaign (see Extended Data Figs. 2 and 6).

Before running all simulations, we validated the base finite element model by comparing the results of the laboratory tests with the results of simulations for the undamaged state and the nine damage scenarios tested in the laboratory (Fig. 2f, Supplementary Information Section 2 and Supplementary Video 3). Specifically, vertical displacements of the lower joints and strains at the midpoints of diagonals and chords were used for the validation (Fig. 2f). The differences in structural response variables (for example, internal forces) between damaged and undamaged states define the way in which loads are redistributed. Two complementary approaches were used to characterize the resistance mechanisms for each damage scenario:

1. 1.

   We can conceptually understand the changes in the response after damage (for example, after the loss of a diagonal component) by analysing the structure, without the damaged component, subjected to joint forces that would counteract the axial force carried by the component before its removal (Supplementary Information Section 2). This provides a sound conceptual picture of the resistance mechanisms activated in each damage scenario and informs the interpretation of the bulk of data provided by the simulation campaign.

2. 2.

   We also followed a quantitative and systematic approach to reveal and track the changes caused by each damage scenario and to support the definition of ALPs and resistance mechanisms. For this purpose, the following set of key performance indicators were defined:

   1. a.

      Increment of vertical displacements, ΔDz, at truss joints:

      $$\Delta Dz_i,j=Dz_i,j^\rmdamaged-Dz_j^\rmundamaged$$

      in which the indices refer to the ith damage scenario and jth measurement point.

   2. b.

      Increment of member axial forces, ΔFx:

      $$\Delta Fx_i,k=Fx_i,k^\rmdamaged-Fx_k^\rmundamaged$$

      in which the indices refer to the ith damage scenario and kth structural member.

   3. c.

      Maximum increment of member bending moments, ΔMyz

      The norm of the bending moment at a given member cross-section j of a member k is expressed as:

      $$Myz_k,j=\sqrtMy_k,j^2+Mz_k,j^2$$

      The increments of bending moment at the start section, j_start, and at the end section, j_end, of the structural member k, for each damage scenario i, are:

      $$\Delta Myz_i,k,\rmj\_\rmstart=Myz_i,k,\rmj\_\rmstart^\rmdamaged-Myz_k,\rmj\_\rmstart^\rmundamaged$$

      $$\Delta Myz_i,k,\rmj\_\rmend=Myz_i,k,\rmj\_\rmend^\rmdamaged-Myz_k,\rmj\_\rmend^\rmundamaged$$

      Finally, the performance indicator is defined as follows:

      $$\Delta Myz_i,k=\left\{\beginarrayll\Delta Myz_i,k,\rmj\_\rmend & \rmif\,| \Delta Myz_i,k,\rmj\_\rmend| > | \Delta Myz_i,k,\rmj\_\rmstart| \\ \Delta Myz_i,k,\rmj\_\rmstart & \rmotherwise\endarray\right.$$

   4. d.

      Increment of joint support vertical reactions, ΔRz:

in which the indices refer to the ith damage scenario and jth support point.

For interpreting the results, we grouped the damage scenarios according to the types of structural member. Each group was also divided into subgroups, which are labelled according to their position:

1. 1.

   Removal of chord segments: south lower (SL), north lower (NL), south upper (SU) and north upper (NU).

2. 2.

   Removal of diagonals: south (S) and north (N).

3. 3.

   Removal of verticals: south (S) and north (N).

4. 4.

   Removal of horizontal bracings: south to north lower (SNL), north to south lower (NSL), south to north upper (SNU) and north to south upper (NSU).

5. 5.

   Removal of vertical bracings: north upper to south lower (NU-SL) and north lower to south upper (NL-SU).

6. 6.

   Removal of stringers: south (S) and north (N).

7. 7.

   Removal of transversal beams: lower (L) and upper (U).

We assessed the effect of each group of damage scenarios on the different performance indicators of each group of members. The values of each performance indicator were represented in three-dimensional illustrations of the bridge and in heat map charts (Extended Data Fig. 7). In the latter, colour temperature and intensity show the magnitude of the indicator for each group of bridge members (horizontal axis) and for each damage scenario (vertical axis). These heat maps are key to identifying patterns and variations along consecutive structural members and across different damage scenarios.

Combining these conceptual and quantitative approaches, we analysed changes in the deformed shape as well as changes in the magnitude of axial forces, bending moments and reactions, to reveal meaningful ALP patterns for each group of damage scenarios.

Simulations for studying the evolution of ALPs

We studied the way in which internal forces are redistributed when external loads increase until the collapse of the bridge. This redistribution is a consequence of the propagation of failures within the whole structural system.

In this case, we carried out nonlinear analyses of a set of ten representative damage scenarios up to the collapse of the bridge. The numerical strategy uses arc-length control on the equilibrium path to be able to track the structural behaviour including consecutive local buckling of structural members. Otherwise, the simulations use the same basic modelling assumptions described in the previous section. The ten damage scenarios (Fig. 4) include three different upper and lower chord failures near the centre of the span (six scenarios) and two different failures of diagonals and verticals near the supports (four scenarios).

We validated the collapse simulations by comparing measurements from the last experimental test, in which loads were increased until collapse, with results from a simulation of the same scenario (Extended Data Fig. 8 and Supplementary Information Section 3).

In this part of the research, we analysed the information at two levels:

1. 1.

   At a global level, we plotted force–displacement curves for the entire structural system for each of the ten representative scenarios. In these curves, displacement corresponds to the vertical displacement measured at mid-span. The force is shown as an overload factor, which represents the multiplier of the reference load of 80 kN used for operational conditions. These curves (Fig. 4) provide information about the evolution of the global stiffness of the structure. They also show the occurrence of local instabilities as snap-through/snap-back events on the equilibrium path, as well as the degradation of global stiffness until collapse.

2. 2.

   At a local level, we defined two new sets of performance indicators that can be compared to understand the progression of damage and changes to the load-redistribution patterns within the system:

   1. a.

      The first indicators characterize changes that occur under the effect of the reference operational load of 80 kN. Specifically, they quantify the differences in internal forces (IF), that is, axial forces or bending moments, between the undamaged and initial damaged condition, normalized by the applied load (that is, 80 kN). This allows analysing changes in load-redistribution patterns independently of the total applied load to the bridge. The sign of the indicator is defined as positive if there is an increase in the magnitude of the load (regardless of whether it is tension or compression), whereas if the total magnitude of the indicator decreases, the index will be negative, indicating an unloading or decrease in demand, for both axial forces and bending moments:

      $$\Delta \rmIF_\text1st line=\rmabs\left(\frac\rmIF_\rmDamaged(80\rmkN)-\rmIF_\rmUndamaged(80\rmkN)80\rmkN\right)\times \rmsgn$$

      $$\rmwith\,\left\{\beginarrayc\rmsgn=1\,\rmif\;\rmabs(\rmIF_\rmDamaged) > \rmabs(\rmIF_\rmUndamaged)\\ \rmsgn=-\,1\,\rmif\;\rmabs(\rmIF_\rmDamaged) < \rmabs(\rmIF_\rmUndamaged)\endarray\right.$$

   2. b.

      The second indicator pertains to the collapse condition. It represents the same differences but, in this case, they are normalized by the collapse load obtained from the simulation considering initial damage:

We extracted conclusions from both approaches to characterize the evolution of ALPs for different damage scenarios (Extended Data Fig. 9) and to identify the mechanisms that are activated by the propagation of failures until collapse.