Witnessing the onset of reionization through Lyman-α emission at redshift 13

Cosmology and conventions

A flat ΛCDM cosmology is used throughout based on the latest results of the Planck Collaboration⁵², with H₀ = 67.4 km s⁻¹ Mpc⁻¹, Ω_m = 0.315 and Ω_b = 0.0492. The cosmic hydrogen fraction is fixed to f_H = 0.76. At z = 13, the Hubble flow is H(z = 13) ≈ 1,990 km s⁻¹ Mpc⁻¹ and on-sky separations of 1″ and 1′ correspond to 3.53 physical kpc and 0.212 pMpc, respectively. We quote magnitudes in the AB system⁵³, emission-line wavelengths in vacuum and EWs in the rest frame unless explicitly mentioned otherwise.

NIRCam observations and target selection

In the following sections, we describe the main JWST and auxiliary Hubble Space Telescope (HST) observations underlying this work. We refer to refs. ^16,54 for details on the NIRCam and MIRI imaging, respectively, whereas ref. ⁵ provides a detailed description of the NIRSpec spectroscopy. Further details on the JADES survey strategy and data reduction are discussed in the survey overview paper¹⁰ and the data release papers^55,56,57.

The NIRCam¹², MIRI¹³ and NIRSpec^17,58 measurements presented in this work are associated with JWST Guaranteed Time Observations (GTO) programme IDs (PIDs) 1180 (PI: Eisenstein), 1210, 1286 and 1287 (PI: Luetzgendorf), further complemented with the JOF programme¹⁴ (PID 3215; PIs: Eisenstein and Maiolino). Also, because the JOF itself is located within the Great Observatories Origins Deep Survey South (GOODS-S⁵⁹) extragalactic legacy field, HST Legacy Field imaging⁶⁰ is publicly available, covering 0.4 μm to 1.8 μm between the Advanced Camera for Surveys (ACS) and Wide Field Camera 3 (WFC3).

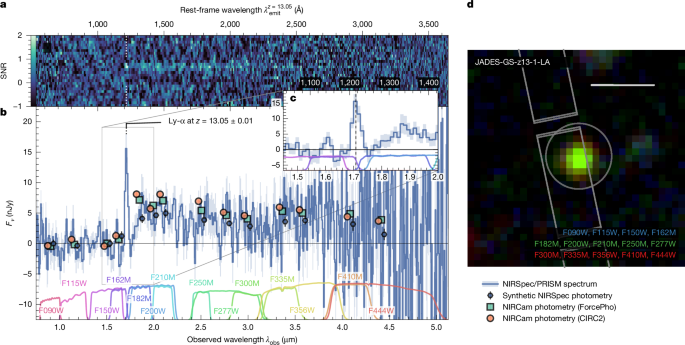
Further MIRI imaging in the F770W filter was obtained⁵⁴ as coordinated parallel observations to JADES NIRCam observations (PID 1180). Several high-redshift targets, selected by refs. ^15,16 based on the NIRCam images in the JOF, including JADES-GS-z13-1-LA (located at right ascension of +53.06475° and declination of −27.89024°), were followed up using the NIRSpec Micro-Shutter Assembly (MSA⁶¹) as part of PID 1287, scheduled between 10 and 12 January 2024.

NIRSpec observations and data reduction

The NIRSpec observations spanned three consecutive visits. However, during visit 2, the lock on the guide star was lost, preventing it from being carried out nominally. Although different MSA configurations were used across visits, JADES-GS-z13-1-LA was observed in both visits 1 and 3 in the PRISM/CLEAR grating-filter combination (simply ‘PRISM’ hereafter) with resolving power of 30 ≲ R ≲ 300 between wavelengths of 0.6 μm and 5.3 μm, as well as in the medium-resolution grating-filter combinations G140M/F070LP, G235M/F170LP and G395M/F290LP (‘R1000 gratings’), each with resolving power R ≈ 1,000. A sequence of exposures following three nod positions was repeated four times for each visit in PRISM mode and once for each of the R1000 gratings. Each nod sequence had an exposure time of 8,403.2 s, consisting of six integrations made up of 19 groups in NRSIRS2 readout mode⁶². Altogether, JADES-GS-z13-1-LA was observed for 67,225.6 s by the NIRSpec/PRISM and 16,806.4 s in each of the R1000 gratings.

We used version 3.1 of the data-reduction pipeline developed by the ESA NIRSpec Science Operations Team⁶¹ and the NIRSpec GTO team (simply ‘pipeline’ hereafter), which produces flux-calibrated spectra largely following the algorithms used in the Space Telescope Science Institute (STScI) pipeline. We refer to previous works^3,5,56,57 for detailed descriptions of the NIRSpec data-reduction pipeline, an overview of which is given in ref. ⁶¹. In brief, three adjacent microshutters were opened to obtain background-subtracted spectra of individual sources, for which the subtraction follows a three-point nodding scheme discussed above. Initial path-loss corrections were calculated under the assumption of a point-source light profile placed at the same intra-shutter location of the source. The PRISM spectra take up an irregular wavelength grid with sampling such that the wavelength-dependent line spread function¹⁷ always spans a fixed number of wavelength bins. Our fiducial (‘sigma-clipped’) spectrum combines all available sub-exposures in the three nodding positions, for which one-dimensional spectra are extracted over the central three spatial pixels (corresponding to 0.3″), through a custom sigma-clipping algorithm (see Supplementary information for details).

Photometric measurements

We obtained photometric measurements of JADES-GS-z13-1-LA using two methods. Our fiducial photometry is determined using ForcePho (B.D.J. et al., manuscript in preparation) on all 14 available NIRCam filters (see also ref. ¹⁶), whereas MIRI/F770W follows a customized procedure following J.M.H. et al. (manuscript in preparation), both discussed in more detail below. An alternative approach to ForcePho is to measure fluxes in circular apertures with a diameter of 0.3″ (‘CIRC2’). These results are summarized in Extended Data Table 1. We include CIRC2 photometry in the available HST bands, which, together with NIRCam filters up to and including F150W, are statistically fully consistent with non-detections (χ² = 11.6 over ten filters, that is, P = 0.31).

Given that the full width at half maximum (FWHM) of the MIRI/F770W point spread function (PSF) is much larger than those of NIRCam⁵⁴, we considered the F444W–F770W colour of JADES-GS-z13-1-LA after convolving the F444W mosaic with the F770W PSF and rebinning to the F770W pixel size. We measured this colour assuming a circular aperture with 0.7″ diameter (‘CIRC5’), which roughly corresponds to the 65% encircled energy of F770W, before applying aperture corrections. The reported MIRI/F770W flux is then inferred from the difference between the total CIRC5 NIRCam/F444W flux and the F444W–F770W colour. Using this approach, we are taking advantage of the higher spatial resolution afforded by NIRCam compared with MIRI. However, this measurement does not yield a significant detection (F_ν = 1.60 ± 2.23 nJy). Neglecting contributions from the [O iii] λ 4,960, 5,008 Å lines and underlying continuum, the MIRI non-detection would be consistent with an Hβ flux of F_Hβ ≲ 6.7 × 10⁻¹⁹ erg s⁻¹ cm⁻² (3σ), translating to an intrinsic Ly-α flux of F_Ly-α ≲ 1.6 × 10⁻¹⁷ erg s⁻¹ cm⁻² (case B recombination; for example, ref. ¹¹).

To explore the morphology of JADES-GS-z13-1-LA, we first fitted Sérsic⁶³ profiles separately to the various available NIRCam filters (using the mosaic images) using the pysersic code⁶⁴. We do not find a strong wavelength dependency of the morphology. In the F277W filter, which explores rest-frame wavelengths around λ_emit ≈ 2,000 Å at z = 13, we constrain JADES-GS-z13-1-LA to have a half-light radius of \({17.5}_{-1.7}^{+3.0}\,{\rm{mas}}\) and a Sérsic⁶³ index consistent with n = 1. This size approaches half the pixel size (that is, 15 mas) and should hence be treated as an upper limit, given that the mosaicing procedure probably introduces artificial smoothing.

To fit to independent dithered NIRCam exposures, we performed further modelling with ForcePho (B.D.J. et al., manuscript in preparation), assuming a model with a single intrinsic Sérsic⁶³ profile and freely varying normalization in each filter (for example, refs. ^65,66,67). Notably, by fitting to the individual exposures, ForcePho avoids correlated noise between pixels in drizzled mosaic images, enabling us to investigate scales smaller than individual pixels. The results are shown in Extended Data Fig. 1 and the resulting photometry is listed in Extended Data Table 1. From this analysis, we find a formal upper limit (84th percentile) on the half-light radius of 5.1 mas. We therefore conclude that the imaging data are consistent with the continuum source being unresolved. On the basis of tests with similarly faint brown dwarf stars that allow the expected systematic uncertainties to be quantified, we conservatively use an upper limit on the half-light radius as reported in ref. ¹⁶ for the F200W filter, ≲10 mas or 35 pc.

Emission-line properties

The emission line at 1.71 μm is clearly and consistently detected across different PRISM data reductions, even when only one of the two individual visits is considered (Supplementary information). We first fit a Gaussian profile to the sigma-clipped spectrum using the corresponding covariance matrix (Supplementary information), which provides a good fit to the data: χ² = 5.97 with five degrees of freedom. We obtain a centroid of 1.7084 ± 0.0014 μm and FWHM = 302 ± 18 Å (or Δv ≈ 5,000 km s⁻¹) that spans 2.4 wavelength bins (120 Å wide at 1.71 μm). We conclude that the line is probably unresolved in the PRISM spectrum and, as expected for compact sources observed with the NIRSpec MSA⁶⁸, that the spectral resolution is enhanced by a factor of approximately 1.5× compared with the resolution curve predicted for a uniformly illuminated microshutter.

To measure the absolute flux of the line, we first applied a correction to both the sigma-clipped spectrum and the covariance matrix based on the linear ForcePho fit found in our path-loss analysis (Supplementary information) to account for further path losses in the NIRSpec measurements. Directly integrating the corrected PRISM spectrum across the four wavelength bins between 1.69 μm and 1.73 μm (each bin with SNR > 1; Supplementary Information), we find a flux of F = 7.42 ± 1.16 × 10⁻¹⁹ erg s⁻¹ cm⁻² (that is, the line is detected at SNR = 6.4). We have verified that all different data reductions (see Supplementary information) yield measurements consistent within 1σ. Specifically, the two visits independently confirm the line detection with measured fluxes of 5.77 ± 1.36 × 10⁻¹⁹ erg s⁻¹ cm⁻² and 9.07 ± 1.80 × 10⁻¹⁹ erg s⁻¹ cm⁻², respectively.

The emission line is not detected in the medium-resolution G140M/F070LP or G235M/F170LP spectra, both of which cover 1.71 μm, as shown in Extended Data Fig. 2 (although we note that the G235M/F170LP transmission drops below 1.7 μm; ref. ¹⁷). To quantify whether this is expected, taking into account their inherently lower sensitivity and relatively short exposure times compared with the PRISM spectra (NIRSpec observations and data reduction), we tested whether the observed R1000 spectra are consistent with the line flux measured in the PRISM spectra. Indeed, we find that, if the observed line profile is sufficiently broadened (FWHM ≳ 600 km s⁻¹, that is, well resolved at R = 1,000 resolution), it would be below the current sensitivity (≲2σ detection expected; Extended Data Fig. 2).

As discussed further in the Supplementary information, we find it highly unlikely that the emission line at 1.71 μm is because of contamination of the microshutter by a foreground source that is aligned with JADES-GS-z13-1-LA by chance and remains undetected in the continuum, given that the continuum emission of JADES-GS-z13-1-LA unambiguously places the source at z ≈ 13. We have performed the ‘redshift sweep’ analysis detailed in the appendices of refs. ^5,9, in which the inferred one-sided P-value for a set of different emission lines is combined to yield the statistical significance of a potential spectroscopic confirmation at a given redshift. The effectiveness of this method is illustrated by the case of JADES-GS-z14-0, for which the most probable redshift was revealed⁵ to be z = 14.178 (combined P = 0.0072), mainly based on a 3.6σ detection of C iii]. This redshift, consistent within the uncertainty determined from fitting the Ly-α break profile with DLA absorption, was later independently confirmed through the detection^21,69 of the [O iii] 88 μm emission line by the Atacama Large Millimeter/submillimeter Array (ALMA). In the case of JADES-GS-z13-1-LA, the redshift sweep was performed across a range of Δz = 0.2 centred on z = 13.0, which, however, did not show any significant line detections.

Upper limits on the flux and EW for other, undetected, lines at z = 13 are therefore determined from integrating the covariance matrix across three PRISM wavelength bins, taking into account any residual flux after having subtracted a power-law model continuum (see ‘Spectral modelling’). The resulting limits, summarized in Extended Data Table 2, are consistent with findings on most other z > 10 galaxies observed by the JWST, which have generally revealed these lines to be relatively weak^3,4,6,23,24.

Spectral modelling

To gain insight into the Ly-α emission and absorption properties of JADES-GS-z13-1-LA, we model the observed spectrum with a simple framework in which Ly-α and continuum emission produced inside the central galaxy are subject to (damping-wing) absorption arising in intervening neutral hydrogen in dense absorbing systems and/or the IGM. We emphasize that the aim of this model is not to be as physically detailed as possible, which would involve performing simulations including three-dimensional radiative transfer coupled to the hydrodynamics of the gas (requiring the relevant feedback processes to be accurately modelled), but rather to constrain the basic physical properties that JADES-GS-z13-1-LA must have to explain the observations.

As we expect the Ly-α line to be redshifted with respect to the systemic redshift of the galaxy (potentially already as Ly-α emerges from the galaxy or otherwise resulting from processing by the neutral IGM^70,71) and no other emission lines are detected (see ‘Emission-line properties’), this quantity (z_sys) is not precisely known and is a free parameter in this model. To remain agnostic about the nature of the ionizing source and to avoid the intrinsic limitations of standard SPS models in reproducing very blue UV continua (Supplementary information), the continuum emission is modelled as a power law, \({F}_{\lambda }\propto {\lambda }^{{\beta }_{{\rm{UV}}}}\), by default. This introduces two more free parameters in the model, the UV slope β_UV and a normalization (at a rest-frame wavelength of λ_emit = 1,500 Å).

To reproduce the smooth Ly-α break seen in the continuum, we allow the continuum emission to be affected by DLA absorption parameterized by the neutral hydrogen column density N_Hi as in refs. ^6,9. The Ly-α emission is explicitly not attenuated by this absorption, as this would completely extinguish the line. Because the attenuated continuum tends to zero at the wavelength of Ly-α, we calculate the line EW according to the unattenuated continuum, which is effectively equivalent to measuring the continuum level by means of the photometry. As discussed in the main text, this would require a specific geometrical configuration such that the Ly-α emission is not strongly absorbed. However, Ly-α emission superimposed on DLA troughs has been observed in galaxy spectra, suggesting that these geometries exist^45,46. The absorption cross-section of neutral hydrogen is based on the Voigt profile approximation given by in ref. ⁷², with a quantum-mechanical correction provided in ref. ⁷³. Because we find that the redshift of the foreground DLA system (when freely varied; for example, ref. ⁷⁴) prefers a solution close to the systemic redshift, z_DLA ≈ z_sys, for simplicity, we fix z_DLA = z_sys in the following.

Alternatively, we considered the case in which the observed spectrum is dominated by the 2γ continuum, which has a fixed shape⁷⁵ and thus only requires one free parameter, the normalization. As a third variant, we considered a combination consisting of a power-law continuum (using the same parameterization as above) and a full nebular emission spectrum, which, as well as the 2γ continuum and the Ly-α line, also contains the free-bound and free-free components. The nebular emission in this case was computed with the PyNeb code⁷⁶, which, however, requires assuming the gas temperature and density. We opted for T = 20,000 K and n = 100 cm⁻³, respectively, for which the 2γ continuum is the dominant contributor in the wavelength range considered here⁷⁷. The choice for this relatively low density is motivated by the fact that the free-bound (and free-free) components mainly contribute at longer wavelengths and would have to be subdominant to reproduce the very steep UV slope. In this multicomponent (‘self-consistent’) model, we tied the continuum normalization to the strength of the Ly-α line, thereby self-consistently scaling the continuum according to the production rate and escape fraction of LyC photons discussed below.

Following refs. ^11,78, IGM transmission was calculated with the patchy reionization model presented in ref. ⁷⁹, integrating along the trajectory of a photon that starts in an ionized bubble of radius R_ion located in an otherwise neutral IGM (see also refs. ^80,81). Following ref. ⁷⁹, we assume the gas in the ionized bubble to be highly ionized (residual neutral fraction fixed at x_Hi = 10⁻⁸) and have T = 10⁴ K, whereas the neutral IGM is at T = 1 K. The gas in both media is assumed to be at mean cosmic density (that is, to have \({\bar{n}}_{{\rm{H}}}\approx 5.25\times 1{0}^{-4}\,{{\rm{cm}}}^{-3}\) at z = 13) and be at rest with respect to the central source. We fixed the global neutral hydrogen fraction of the IGM (that is, outside the ionized bubble⁷⁸) to \({\bar{x}}_{{\rm{HI}}}=1\), motivated by various types of evidence that consistently indicate that, globally, the Universe is still highly neutral well below redshift z = 13 (for example, refs. ^82,83).

We self-consistently model the size of the ionized bubble by considering the production rate and escape fraction of hydrogen-ionizing photons of the central galaxy. As in ref. ¹¹, we define \({\xi }_{{\rm{ion}}}\equiv {\dot{N}}_{{\rm{ion}}}/{L}_{\nu ,{\rm{UV}}}\), in which \({\dot{N}}_{{\rm{ion}}}\) is the production rate of ionizing photons and L_ν,UV is the luminosity density (in units of erg s⁻¹ Hz⁻¹) of the intrinsic continuum of the ionizing source at λ_emit = 1,500 Å. In the case of the multicomponent model in particular, L_ν,UV is taken to be the value of the power-law continuum at 1,500 Å such that ξ_ion reflects the intrinsic value. The rate of ionizing photons leaking from the galaxy at a given production efficiency ξ_ion is modulated by the LyC escape fraction, f_esc,LyC. In a given model instance, we therefore begin by deriving the rate of ionizing photons escaping the galaxy using (for example, refs. ^26,84,85,86)

To calculate the bubble radius R_ion, we then numerically integrate equation (3) in ref. ⁸⁰, describing the time evolution of R_ion(t) to obey

thereby taking into account the effect of the expansion of the Universe parameterized by the Hubble parameter H(z) and recombinations within the ionized bubble, for which we assume a clumping factor for ionized gas of C_Hii = 3 (for example, ref. ⁸⁷) and case B recombination rate α_B at 20,000 K, as given by in ref. ⁸⁸. The typical recombination timescale at z = 13, \({({C}_{{\rm{HII}}}{\bar{n}}_{{\rm{H}}}{\alpha }_{{\rm{B}}})}^{-1}\approx 140\,{\rm{Myr}}\), indicates that JADES-GS-z13-1-LA as an ionizing source could quickly ionize its surroundings before recombinations are able to restore balance. As illustrated in Extended Data Fig. 4, showing the time evolution of R_ion in the default model, the bubble radius can reach R_ion ≈ 0.1 pMpc over a timescale of only 1 Myr. We note that, when the supply of LyC photons stops, the residual neutral hydrogen fraction rapidly increases owing to the high density at z = 13 (x_Hi ≈ 0.01 after 1 Myr), implying that, for an ionized bubble to have a substantial transmission-enhancing effect redwards of the systemic Ly-α wavelength⁷⁹, it must be actively maintained. Here we integrate until we reach a fiducial age of t = 10 Myr, having verified that changing this assumption has little impact on our findings as a result of the sublinear scaling R_ion ∝ t^1/3 (in the absence of recombinations and the Hubble flow). We also considered an alternative model identical to the default power-law model but for which we fix R_ion = 0 (that is, f_esc,LyC = 0).

Finally, we determine the intrinsic Ly-α luminosity resulting from recombinations by considering the number of ionizing photons that are absorbed within the galaxy and reprocessed into Ly-α. Similarly to the above, the effective rate of LyC photons contributing to the recombination rate within the galaxy (\({\dot{N}}_{{\rm{rec}}}\)) follows from the product of the intrinsic production rate \({\dot{N}}_{{\rm{ion}}}\) and absorbed fraction (one minus the escape fraction) of ionizing photons. This is multiplied by the fraction of (case B) recombination events that result in the emission of a Ly-α photon, f_rec,B (see, for example, ref. ⁸⁹), to arrive at the emission rate of Ly-α photons and hence the Ly-α luminosity (that is, the emission rate multiplied by the energy of a Ly-α photon),

We used f_rec,B(T = 20,000 K) = 0.647 based on the prescription in ref. ⁹⁰, noting that it depends only weakly on temperature⁹¹ and that case A would lead to an unaccounted increase in f_esc,LyC. Under the very conservative assumptions of no IGM absorption at all and f_esc,LyC = 0, equation (3) places a lower limit on the LyC production efficiency through the observed Ly-α luminosity relative to the continuum, yielding ξ_ion ≳ 10^25.1 Hz erg⁻¹ (10^25.4 Hz erg⁻¹ under case A). The Ly-α line, as it emerges from the galaxy, is modelled as a Gaussian profile with a given velocity dispersion σ_Ly-α, which is shifted in velocity space at a given offset from the systemic redshift, Δv_Ly-α,int, and normalized to the Ly-α luminosity derived as described above.

Radiative transfer calculations predict that a wide variety of Ly-α spectral profiles may emerge from galaxies^92,93, but galactic outflows typically cause systematically redshifted components^94,95, as seen ubiquitously at high redshift^{70,71,96,97,98,99}. Although the emergent Ly-α spectral profile is fundamentally unknown at z ≳ 7 owing to the asymmetric IGM transmission on the blue side^78,79, some clues are given by the non-detection of the line in the R1000 spectra. If the line were unresolved at a resolution of R ≈ 1000, that is FWHM ≲ 300 km s⁻¹, we would have probably seen a marginal detection (Extended Data Fig. 2). Instead, the line profile probably contains a prominent red, broad component to allow for sufficient transmission of Ly-α flux at z = 13 even in the presence of an ionized bubble (Fig. 2). We note that, because of the IGM transmission, the peak of the intrinsic line profile at velocity offset Δv_Ly-α,int with respect to systemic redshift effectively gets further redshifted to a velocity offset of Δv_Ly-α,obs.

We used the PyMultiNest¹⁰⁰ implementation of the multimodal nested-sampling algorithm MultiNest¹⁰¹ to perform a Bayesian fitting routine to the sigma-clipped PRISM spectrum and corresponding covariance matrix (see Supplementary information) from 1.609 μm up to 2.897 μm (127 wavelength bins), or 1,150 Å ≲ λ_emit ≲ 2,000 Å at z = 13. Before fitting, as in the section ‘Emission-line properties’, we corrected the NIRSpec measurements for further path losses. Meanwhile, the model spectrum is convolved with the PRISM resolution curve predicted for a uniformly illuminated microshutter, enhanced by a factor of 1.5 based on the measured width of the Ly-α line in the PRISM spectrum (see ‘Emission-line properties’). As detailed by Jakobsen et al. (manuscript in preparation), the goodness-of-fit statistic χ² is calculated as the matrix product

in which Σ⁻¹ is the inverted covariance matrix and the ith element of the vector R is given as the difference between observed flux density in the ith wavelength bin (\({F}_{\lambda ,i}^{\text{obs}}\)) and the modelled one (\({F}_{\lambda ,i}^{\text{model}}\)),

The model log-likelihood ℓ is calculated assuming that the observed data are normally distributed around the model, \({\ell }=-\frac{1}{2}{\chi }^{2}\). All model parameters, prior distributions and resulting best-fitting values are summarized in Extended Data Table 3. The posterior distributions for the default model are shown in Extended Data Fig. 3.

Although the multicomponent self-consistent model has a slightly higher χ² (171.4) than the default power-law model (χ² = 168.1), notably, it favours a high LyC escape fraction (\({f}_{{\rm{esc,}}{\rm{LyC}}}=0.7{3}_{-0.26}^{+0.14}\)) to suppress the nebular continuum, much like the SPS model fits (Supplementary information). Indeed, fixing R_ion = 0 in the self-consistent model (results not included here) yields a much poorer fit (χ² = 183.1), as this overpredicts the continuum tied to the strong Ly-α line. Moreover, the intrinsic Ly-α flux required for the R_ion = 0 power-law model is discrepant at a 4.5σ level with the MIRI/F770W non-detection (see ‘Photometric measurements’).