Wide-swath satellite altimetry unveils global submesoscale ocean dynamics

SWOT data

This study uses data from 14 complete cycles of the SWOT science orbit, from 26 July 2023 to 8 May 2024. One complete cycle comprises 584 passes and takes 21 days to complete. We use two SWOT data products. (1) ‘Level 2 KaRIn Low Rate Sea Surface Height Data Product – Unsmoothed’, on a 250-m grid, version PIC0. The L2 product baseline C was produced by NASA and CNES (hereafter L2). (2) ‘Level 3 sea surface height expert’, on a 2-km grid, version 1.0, produced by the DUACS and SWOT Science Teams (hereafter L3)⁵².

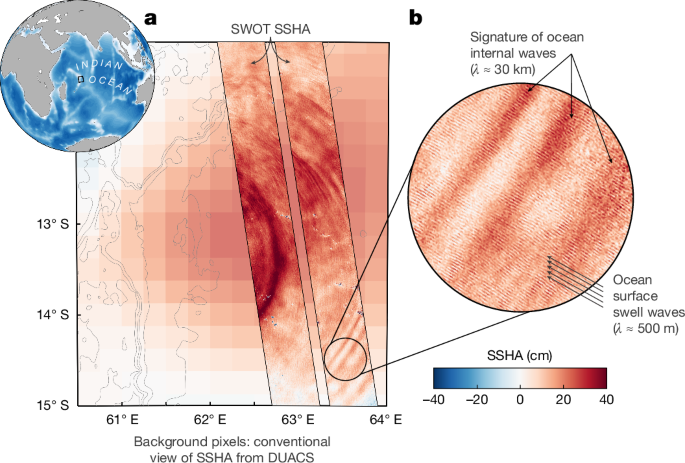
The L2 variable ‘ssh_karin_2’ was used in Figs. 1 and 3, which is the fully corrected SSH from KaRIn relative to the reference ellipsoid, using model-based wet troposphere correction (variables ‘model_wet_tropo_cor’ and ‘sea_state_bias_cor_2’), as per recommendation from the SWOT project. We remove the mean sea surface (MSS; variable ‘mean_sea_surface_cnescls’ or ‘CNES_CLS_2022’). We remove an along-track linear trend at each cross-track pixel; this removes the roll error but also some large mesoscale signal, but for our purpose of studying small-scale ocean dynamics in Figs. 1 and 3, this is not an issue. We do not apply quality control flags because we want to show all of the data. At certain times and locations, this unsmoothed 250-m gridded dataset contains long swell waves (for example, Fig. 1), which are filtered out in the 2-km product.

The L3 ‘ssha_unedited’ was used in Figs. 2 and 4, which is the L2 smoothed SSHA 2-km product but with the L3 empirical calibration replacing the L2 calibration. This is important because L3 has been reconciled with the DUACS SSHA product to allow direct comparison and has been shown to be an improvement⁵³. It should be noted that, although the empirical calibration might absorb a fraction of the difference between SWOT and DUACS, it will be small compared with other factors (for example, L4 smoothing)^52,54. The SSH anomaly is from the MSS. We add back in the stationary internal tide SSH signal (‘internal_tide_hret’) that was removed as part of processing. We apply the variable ‘quality_flag’, which is used to identify and remove bad data, when computing the global variability (Fig. 2; all data points with a quality flag ≠ 0 are removed). We do not apply the flag for the study of the submesoscale eddy (Fig. 4) because it removes the core of the eddy as an outlier. Because SWOT coverage and accuracy is beyond the capability of the existing MSS product, there are residual small-scale bathymetric features in the SSHA data⁵⁵. To correct for this, we compute a time mean for all cycles (N = 14), high-pass-filter it with a 50-km two-dimensional Gaussian kernel and subtract it from each pass. This process removes the small-scale bathymetric features from the SSHA while mostly bypassing the large-scale and mesoscale time mean. This is sufficient for our purposes, but it may remove a fraction of the ocean time mean signal; in the long run, a more accurate MSS product will be produced using the SWOT data⁵⁵.

DUACS data

DUACS is the operational multimission production system for altimeter data developed by CNES/CLS (ref. ³⁵). We use the DUACS near-real-time L4 dataset available from the Copernicus Marine Service. The data are provided daily on a 0.25° grid. We interpolate DUACS SSH onto SWOT grids at 2-km posting for the direct comparison in Fig. 2.

Quantifying SWOT SSH beyond DUACS

To quantify the amount of variability seen by SWOT beyond DUACS (Fig. 2a), we compute the RMS in space (0.5° × 0.5°) and time (14 cycles; 26 July 2023 to 8 May 2024) of the difference between SWOT and DUACS SSHA. Figure 2b shows the RMS of 50-km high-passed SWOT SSHA only (filtering performed with a two-dimensional Gaussian kernel in both directions, although across swath, the window shortens towards the edges; we discard data 10 km from every edge).

This new view of small-scale ocean variability (Fig. 2) contains within it a wealth of information that will take years to precisely unpack, but which we know includes small-scale ocean currents and internal gravity waves (Figs. 3 and 4) and SWOT residual errors³²—comprising residual instrument error including noise (for example, there are some noticeable track errors in the high latitudes) and residual geophysical signals not fully corrected for, including the wet troposphere effect, for which scales less than about 30 km are not well accounted for in model or radiometer measurements.

For the two case studies shown here (Figs. 3 and 4), the signal strength of each feature is O(10 cm). For context, the error standard deviation of SWOT at 6-km resolution is less than 0.5 cm. So, these examples are well above the noise floor. However, caution should be taken when analysing SWOT data globally, as both signal and errors are time- and space-dependent.

(Cyclo)geostrophy and gradient wind

Mesoscale and submesoscale eddies are detected by satellite altimeters through SSHA, which serves as a proxy for surface pressure. SSHA is connected to eddy velocities (U) through the momentum equations, which incorporate nonlinear advection terms and Coriolis forces (f)⁵⁶:

in which g is the acceleration owing to gravity and k is the vertical unit vector. When velocity gradients (∇U) are much smaller than the Coriolis parameter f (leading to R ≪ 1, in which R = ∇U/f), eddies are in geostrophic balance, for which Coriolis forces counterbalance pressure forces. The geostrophic velocity is:

However, when velocity gradients approach or exceed f, the nonlinear terms become substantial, acting as centrifugal forces, similar to atmospheric hurricanes. This results in eddies characterized by a new dynamical state known as gradient wind balance^2,3,56,57. Usually, large ocean eddies are in geostrophic balance and small eddies are in gradient wind balance. For an isolated eddy, such as the one depicted in Fig. 4 with a 15-km radius, in which the gradient of the geostrophic velocity is close to f, the flow cannot be considered in geostrophic balance. The gradient wind balance—called the cyclogeostrophic balance for an isolated circular eddy—can be denoted⁵⁶:

in which r is the radius of curvature. Solving for V(r)⁵⁶:

With the Coriolis parameter f = 10⁻⁴ s⁻¹, we found V ≈ 0.5 m s⁻¹ for r = 15 km (instead of about 1 m s⁻¹ for the geostrophic velocity). Note that the geostrophic Rossby number is Ro = 0.6 for this cyclone. Smaller eddies, such as those shown in Extended Data Fig. 2, exhibit larger magnitudes of the geostrophic velocity gradients, which can reach 2f or 3f and even higher. These characteristics suggest calling these eddies ‘ocean hurricanes’.

A recent airborne experiment⁴⁷ uncovered a turbulent field of strongly interacting submesoscale eddies in gradient wind balance (equation (1)). In such eddy turbulence, the velocity gradients associated with these eddies involve not only the relative vorticity and the spin of the eddies but also the strain, which governs the stretching of an eddy by adjacent eddies, and divergence, which is linked to vertical motions. These gradients exhibit magnitudes larger than f and play a critical role in the interactions of smaller eddies with larger eddies. The challenge for SWOT is recovering these gradients of equation (1) from only SSHA.

Cautionary remarks on SWOT velocity

Our application of geostrophy and cyclogeostrophy with SWOT SSHA is predicated on two assumptions: (1) the SSHA signal observed by SWOT is primarily because of ocean currents and (2) the ocean currents can be explained by the simple steady-state balances. We are confident that, for the case study selected here (shown in Fig. 4), the first assumption holds true, based on the large amplitude of the eddy and concurrent observations from sea surface temperature and chlorophyll a imagery. When we compute velocity, we smooth the L3 SSHA field with a two-dimensional boxcar filter of 6 km (three grid points) before taking the horizontal gradients. This suppresses any residual noise resulting from high surface waves. Chelton et al.⁵⁸ used postlaunch noise estimates to show that resolvable feature diameters are 8.5 km and larger in velocity. Our case study has a diameter of 30 km. We emphasize, however, that the first assumption is certainly not true for all SWOT-observed eddies, owing in large part to the entanglement of wave signals in the SSH at scales <100 km but also instrument measurement errors (for example, wet troposphere effect, sea state bias etc). The relative contribution of these factors is variable in space and time and is an area of active research. We show that the second assumption does not hold for geostrophy. We propose gradient wind/cyclogeostrophy as an improved approximation, as suggested by a recent airborne experiment⁴⁷ and literature².

Vertical velocity

We estimate vertical velocity by tracking the time change of relative vorticity of an eddy over two successive SWOT passes (Extended Data Fig. 4). The dynamical balance between the change of relative vorticity and vertical stretching (or surface divergence with the minus sign) gives:

in which ζ is the relative vorticity, f is the Coriolis parameter, w is the vertical velocity and z and t are vertical and time coordinates, respectively. The time change of ζ is equal to the vertical stretching term. Assuming that the divergence is constant from the surface down to a given depth, H, we obtain an expression for the scale of vertical velocity, taking w = 0 at the surface, as:

The area-averaged cyclogeostrophic relative vorticity associated with the Kuroshio small eddy—estimated to be half the geostrophic relative vorticity (see above)—is about 1f and changes by +0.1f in 10.8 h. Using a range of mixed-layer depth values from the Argo climatology at the location of the eddy we observe here⁵⁹, from 50 to 125 m, we obtain a range of vertical velocity values from −6 to −14 m per day.

Internal wave energetics

We follow refs. ^39,40 to calculate the energy flux by internal solitary waves and tides. For linear waves, the dominant energy flux is the pressure work and can be calculated by \({\int }_{-H}^{0}{u}^{{\prime} }{p}^{{\prime} }{\rm{d}}z\), in which u′ and p′ are the velocity and pressure perturbations associated with the internal waves, respectively. For nonlinear waves, the full energy flux includes two more terms, \({\int }_{-H}^{0}{u}^{{\prime} }({K}_{{\rm{e}}}+{P}_{{\rm{e}}}){\rm{d}}z\), in which K_e and P_e are the kinetic energy and available potential energy, respectively, of the nonlinear waves that can be calculated using wave SSH and stratification⁶⁰. The stratification is used to estimate the vertical structure associated with the wave SSHA. The velocity fields used for kinetic energy can be derived from SSHA using dispersion relationships for inertial gravity waves and nonlinear solitary waves. The potential energy is associated with the vertical displacement of isopycnals that can be estimated by the vertical modal structures and SSHA. In the end, all energy flux can be calculated using SSHA and stratification. The details of the formulation can be found in previous studies^39,40,60.

Here we compute the energy flux of the internal solitary wave packet in the Andaman Sea observed by SWOT and shown in Fig. 3b,d. The mean vertical density profile and stratification is from the World Ocean Atlas 2023 climatology (WOA23). We tested using a total and seasonal mean profile and found no substantial difference. Using the observed SSHA peak amplitude of 20 cm (Fig. 3c) and the climatological mean density profile in a water depth of 700 m, we compute the internal solitary wave maximum vertical displacement, η₀, to be −39 m, its phase speed, c_p, as 2.26 m s⁻¹ and its half-width as 648 m. The depth-integrated kinetic energy and potential energy density are 42.9 and 31.5 kJ m⁻², respectively. The depth-integrated linear energy flux and the total energy flux at a peak amplitude of 20 cm are 140 and 176 kW m⁻¹, respectively. For waves with a peak amplitude of 10 cm, these numbers are reduced to 32 and 37 kW m⁻¹, respectively. To estimate a time average over one wave period, for this solitary wave packet of five waves generated every 12.4 h, the magnitude is reduced over each solitary wave hyperbolic secant profile by a factor of 3.5 and further reduced by a factor of 5 owing to the time gap without any nonlinear waves. This gives 8 kW m⁻¹ linear energy flux and 10 kW m⁻¹ total energy flux for a solitary wave packet of five waves of 20-cm peak amplitude and 1.8 kW m⁻¹ linear energy flux and 2 kW m⁻¹ total energy flux for the same wave packet but with 10-cm peak amplitude. The linear energy flux is more than twice as large as the previously estimated coherent M₂ tides⁴⁰ from altimetry, which were approximately 0.8 kW m⁻¹. The magnitudes of the total fluxes, ranging between 2 and 10 kW m⁻¹ from SWOT, are generally consistent with existing simulations in the Andaman Sea^61,62. However, for the first time, this highly heterogeneous internal wave energy budget can be estimated at high spatial resolution from observations, which will contribute to the improvement of global ocean estimates.