Tunable vacuum-field control of fractional and integer quantum Hall phases

In the newly emerged field of cavitronics⁵, research has been leveraging the ultrastrong light–matter coupling regime⁷, aiming to modify molecular structures⁸, enhance electron–phonon couplings⁹ and facilitate the emergence of new electronic phases, including superconductivity¹⁰, ferroelectricity¹¹ and topological properties^12,13. Despite substantial theoretical backing and evidence of cavity-induced alterations in chemical reactions^3,14 and charge transport^{13,15,16,17,18,19}, demonstration of the manipulation of strongly correlated phases²⁰ by cavity vacuum fields remains scarce.

In this work, as illustrated in Fig. 1, we have developed a mobile cavity system capable of finely tuning the strength of cavity vacuum fields permeating a small Hall bar, driving the system in situ from a completely uncoupled state to an ultrastrongly coupled one, hence allowing a fully self-referenced assessment of the impact of vacuum fluctuations on the material system. This is achieved by adjusting the distance between a metallic split-ring resonator and the high-mobility GaAs-based two-dimensional electron gas (2DEG) within a quantum well heterostructure. When subjected to a strong perpendicular magnetic field, this set-up allows for the probing of the integer quantum Hall effect and of strongly correlated fractional quantum Hall (FQH) phases by means of transport measurements of longitudinal and transverse resistance. We have discovered that the ‘hovering’ cavity resonator decreases the exchange splitting at odd filling factors while significantly enhancing several fractional quantum Hall phases with respect to their value in the uncoupled Hall bar. This enhancement occurs while maintaining the metallic resonator at distances for which electrostatic screening effects are entirely negligible. We leverage activated-transport measurements of both integer quantum Hall and FQH gaps as exemplary cases to demonstrate the influence of cavity vacuum fields on condensed matter systems, and how to exploit them to address in situ quantum states in small devices.

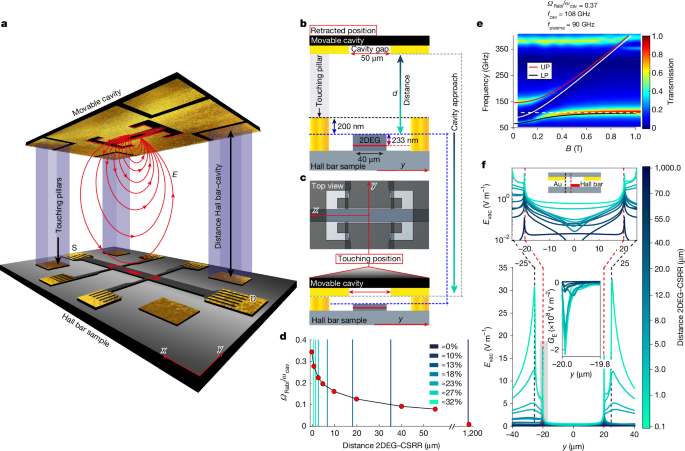
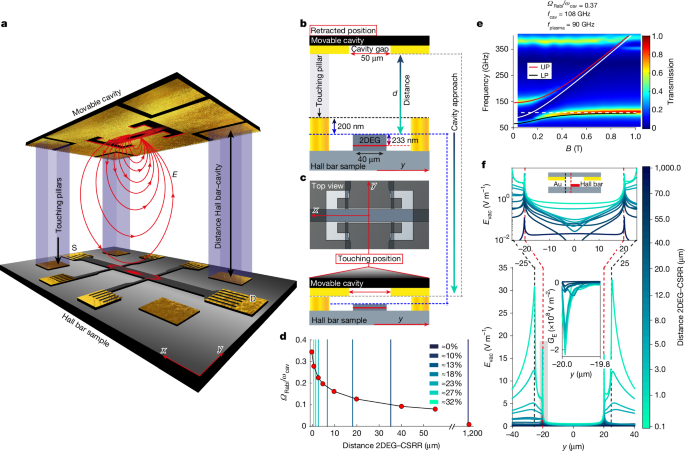
a, Artistic rendering of the platform implemented to tune the coupling strength between the electrons of the 2DEG within a Hall bar and the vacuum electromagnetic fields of a CSRR. The CSRR, defined by a cutout in a gold layer, approaches the Hall bar from above, increasing the coupling to its fringing electric field, E (red arrows). S, source; D, drain. b, Side profile along the y axis: the resonator plane, with a 50-μm cavity gap (red), is positioned above the Hall bar, which has a width of 40 μm and gold-coloured pillars protruding next to it. The resonator plane is shown in a retracted position, not in contact with the sample, with a separation d from the Hall bar surface. c, As the cavity moves closer, the resonator plane touches the pillars, establishing electrical contact. At the top, an overlaid view of the Hall bar and CSRR is displayed, with the grey shading representing the CSRR metal, showing their alignment (Methods). d, Simulated normalized coupling strength as a function of the distance between the resonator and the 2DEG. The coloured vertical lines correspond to the distances d + 233 nm (the quantum well is located at a depth of 233 nm below the surface) at which the magnetotransport traces in Figs. 2a and 3a were measured in the experiment. e, Simulated polariton dispersion of the coupled system with the cavity being 0.1 μm away from the 2DEG. UP, upper polariton; LP, lower polariton. f, Simulation of the cavity vacuum electric field profile across the Hall bar at magnetic field B = 0.3 T. The black dashed line indicates the gap region of the CSRR, and the red dashed line marks the edge of the 2DEG. Top: zoom-in of the area around the Hall bar. Inset bottom: gradient of the vacuum electric field exponentially decaying into the 2DEG (shaded area).

This experiment demonstrates that quantum light–matter interaction can reduce spin splittings and enhance certain fractional quantum Hall gaps, and our theoretical analysis shows that this effect can arise from a cavity-mediated attractive potential. Further investigations using complementary techniques, such as capacitance measurements^21,22,23,24 and inelastic light scattering^25,26,27,28, which have been used to study fractional quantum Hall states at filling factors ν < 1, will be essential for achieving a comprehensive understanding of these effects.

Our primary focus is to highlight the impact of vacuum fields on solid-state systems, using integer and fractional quantum Hall effects as key examples. In this context, it is important to note that the energy gaps of FQH states are highly sensitive to system parameters. When measured through activated transport, the activation energy extracted by means of Arrhenius law fitting corresponds to the energy required to create a widely separated composite-fermion quasiparticle–quasihole pair²⁹. This activation energy—corresponding to the energy gap—can vary across different systems, even for the same material. It depends on factors such as electron mobility^30,31,32, effective layer thickness³³, local disorder^34,35 and Hall bar geometry, as demonstrated with the reference measurements on the same heterostructure in van der Pauw geometry reported in Extended Data Fig. 1 (see the Supplementary Information for details on analysis and measurement). Additionally, these gaps strongly depend on the nature of electron–electron interactions. Previous theoretical research³⁶ has highlighted the potential to enhance these gaps in monolayer two-dimensional (2D) materials such as graphene by leveraging the electrostatic screening effects of a closely positioned dielectric layer, of the order of the electron’s magnetic length. However, such a strategy is generally infeasible for GaAs quantum wells, which are embedded within a thicker semiconductor layer with a high dielectric constant that prevents close-proximity adjustments. Furthermore, the substitution of a dielectric layer with a metallic one is expected to reduce the gap³⁶. Indeed, we have independently recalculated the fractional quantum Hall gaps taking into account the Coulomb potential modified by the image charges produced by a metallic plate and found agreement with ref. ³⁶ for their case α = −1. In this case, there is a reduction of the Laughlin gap. Moreover, when the distance is much larger than the magnetic length, as in our experiments, the magnitude of the change is totally negligible (Extended Data Fig. 2). Additional details are provided in the Supplementary Information.

In our experiment, we utilize a metallic resonator positioned at a distance from the 2DEG, typically orders of magnitude larger than the magnetic length, a range at which electrostatic modifications to the Coulomb potential become negligible. Moreover, contrary to expectations of electrostatics in the presence of a metal plate, the metallic resonator does not decrease but rather increases the fractional quantum Hall gaps. We interpret this remarkable effect as stemming from the emergence of a cavity-induced long-range attractive electron–electron potential mediated by the exchange of virtual cavity photons. In particular, the presence of strong spatial gradients of the vacuum fields is essential to create a cavity-mediated electron–electron interaction within the same Landau level, which is, in the absence of those gradients, forbidden by Kohn’s theorem¹⁹.

The experimental set-up depicted in Fig. 1a is designed to vary the spacing between a Hall bar and a cavity, specifically a complementary split-ring resonator (CSRR) evaporated on a GaAs substrate. Adjusting this distance allows us to modulate the intensity of the cavity’s fringing fields, which extend beyond the resonator’s gap (illustrated by red lines). These fields penetrate the Hall bar and interact with the electron gas. Figure 1c shows the alignment of the CSRR’s 50-μm gap with the 40-μm-wide Hall bar, which was crafted using conventional photolithography on a GaAs-based heterostructure. The quantum well beneath the surface, located at a depth of 233 nm, exhibits a high electron mobility of 1.69 × 10⁷ cm² V⁻¹ s⁻¹ and a sheet density of 2.06 × 10¹¹ cm⁻² at 1.3 K without illumination.

Adjacent to the Hall bar are four etched pillars rising 200 nm above the surface, effectively spacing the CSRR’s gold plane from the Hall bar to prevent physical contact and serving as alignment references for the initial set-up. Finite-element simulations, detailed in Fig. 1d, explore the coupling strength Ω_Rabi/ω_cav as a function of distance—in which Ω_Rabi represents the Rabi frequency³⁷, and ω_cav = 2πf_cav denotes the cavity’s angular frequency. By fitting the Hopfield model’s anti-crossing curve to the polaritonic dispersion (Fig. 1e), it is demonstrated that the system can be finely adjusted from a nearly decoupled state (Ω_Rabi/ω_cav ≈ 0 at a 1,200-μm cavity distance) to an ultrastrong coupling regime³⁸ (Ω_Rabi/ω_cav = 37% as the cavity approaches within 0.1 μm of the 2DEG). As the resonator approaches, the cavity’s resonance frequency shifts downward from 145 GHz to 115 GHz, a change attributed to the fact that the mode field reaches the semiconductor region. Note that measurements were taken at a minimal CSRR-to-Hall bar surface distance of d = 0.35 μm, achieving a coupling strength of 32%, in which d indicates the separation between the CSRR and the Hall bar surface, ensuring that the resonator plane and the Hall bar sample remain spatially separate (Fig. 1b). By contrast, the simulations pertain to the CSRR’s distance from the 2DEG, which is effectively increased by an additional 233-nm semiconductor layer atop the 2DEG.

In Fig. 1f, we study the vacuum electric field (E_vac) profile across the Hall bar at a magnetic field B = 0.3 T for different distances d, focusing on the lower polariton branch, while noting that the upper polariton branch shows very similar results as shown in the Supplementary Information.

As the resonator plane is moved closer to the Hall bar, the amplitude of the electric field gradually increases. Around the Hall bar, centred at zero and spanning 40 μm, four symmetric maxima emerge at the 2DEG level. Peaks at ±25 μm align with the CSRR gap edges, and maxima at ±20 μm correspond to the Hall bar edges, where the CSRR’s vacuum electric field E_vac interacts with the 2DEG’s electrons and then rapidly decays into the bulk, leading to a maximum field gradient of the order of 10⁸ V m⁻² (Fig. 1f, inset bottom) and to a remaining electric field of the order of 0.8 V m⁻¹ within the bulk of the Hall bar when the system is 37% coupled.

During a single cool-down in a dilution refrigerator, we measure the longitudinal resistivity ρ_xx on the side of the Hall bar and the transverse resistance R_H across the Hall bar as a function of the magnetic field. Each trace is taken for a specified distance d and can be associated with the corresponding coupling according to the simulations in Fig. 1d. Measurements are conducted at an electronic temperature of ≈20–45 mK, very close to the mixing chamber temperature. Slight temperature variations below 50 mK due to eddy currents during magnetic field ramping are consistent across all measurements, and the experimentally measured temperature is always considered in the analysis of activation gaps.

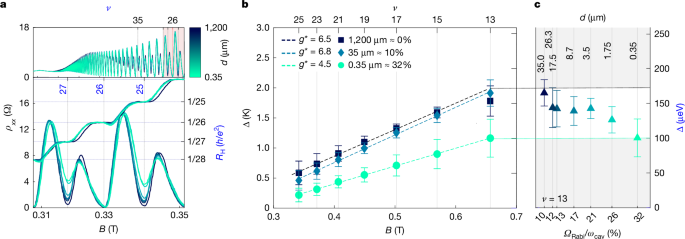
As illustrated in Fig. 2a (top), at lower magnetic fields and as the resonator plane is gradually brought closer to the Hall bar, increasing the coupling strength, we observe a consistent increase in the minima of the longitudinal resistivity and a gradual degradation of the quantized plateaux (Fig. 2a, bottom). The data suggest that for odd quantum Hall plateaux, the modification of the electron–electron potential by the cavity has the effect of weakening the quantization, as was already observed in a more marked fashion in our previous experiments¹⁸ in which the cavity was directly fabricated onto the Hall bar (see also the Supplementary Information for further comparison between the two results). We remark that, as recently reported³⁹, at magnetic fields at which quantization is present, we do not see evidence for a renormalization of the von Klitzing constant R_K of either integer or fractional plateaux.

a, Longitudinal resistance (left vertical axis) and Hall resistance (right vertical axis) for different distances d. As the coupling increases, at odd integer values of the filling factor ν, the longitudinal resistance at the minima rises and the correspondent quantum Hall plateaux lose quantization. b, Plot of the activation temperatures (left axis)—equivalently, energies (right axis)—extracted from the Arrhenius plot (Supplementary Information) for odd filling factors ν = 25 to ν = 13. The effective g-factor is obtained from a linear fit indicated with dashed lines and reported in the legend together with d and the normalized coupling strength. c, Evolution of the activation energy of ν = 13 as a function of the coupling and corresponding distance d. The error bars in b,c correspond to the standard deviation of the Arrhenius law fit (not weighted), and therefore describe the goodness of the fit.

This behaviour at odd filling factors suggests a reduction in effective spin splitting with increased cavity coupling. Indeed, the effective spin splitting Δ is experimentally obtained by studying the thermally activated minima of the longitudinal resistance, which exhibit a characteristic exponential decay as a function of the inverse temperature (see the Arrhenius plots in the Supplementary Information). As shown in Fig. 2b, we observe a linear dependence of the gap Δ as a function of the magnetic field whose slope μ_Bg^⋆/k_B (in which k_B is Boltzmann’s constant and μ_B is the Bohr magneton) directly yields⁴⁰ the effective gyromagnetic factor of the electron g^⋆ whose value includes corrections from the exchange energy⁴¹.

We find the effective g-factor to decrease from g^⋆ = 6.5 when the system is uncoupled (with the resonator plane about 1.2 mm away; Fig. 2a,b) to g^⋆ = 4.5 when the system is ultrastrongly coupled, with the resonator plane positioned 0.35 μm from the Hall bar surface (approximately 0.6 μm from the 2DEG), suggesting a strong reduction of the exchange energy corrections through the cavity-induced electron–electron potential.

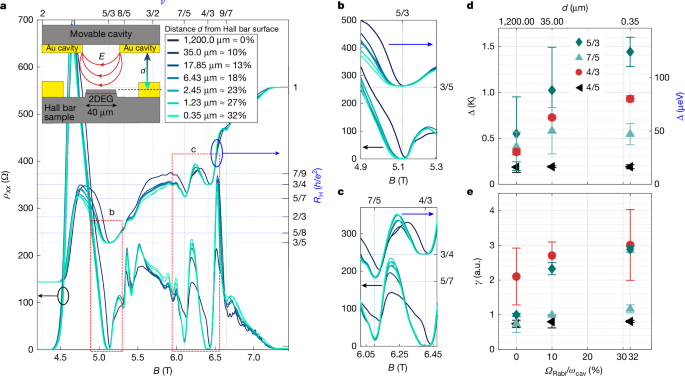
In contrast to the observed degradation of the quantization for the integer quantum Hall plateaux with increased light–matter coupling, the influence of the cavity vacuum fields on fractional quantum Hall states is profound and consists of an overall improvement of the quantization of the fractional states 5/3, 7/5 and 4/3, as depicted in Fig. 3a–c. This improvement was observed in a consistent manner in our temperature study and for the two resonators measured (Supplementary Information). At the lowest temperature, with progressively increased coupling, we observe a noticeable widening of the plateaux alongside a reduction in the resistance minima of ρ_xx (Fig. 3b,c).

a, Longitudinal resistance (left vertical axis) and Hall resistance (right vertical axis) in the magnetic field region exhibiting the fractional quantum Hall states, for different distances d between the movable cavity and the Hall bar. Inset: side view schematic of the set-up. b,c, Zoom-in of the fractions 5/3 (b) and 7/5 and 4/3 (c). d, Activation energy gaps for fractional fillings 5/3, 7/5, 4/3 and 4/5 as a function of the normalized coupling Ω_Rabi/ω_cav and corresponding distance between the split-ring resonator and the Hall bar. e, Decay rate γ of the power law dependence ρ_xx = αT^γ for the same fractions reported in d. The error bars in d,e indicate the 95% confidence interval of the weighted fit (Supplementary Information) of the Arrhenius law or, respectively, the power law. a.u., arbitrary units.

We assess the energy gap by measuring the thermally activated longitudinal resistance (Extended Data Fig. 3), which exhibits a characteristic exponential dependence on the inverse temperature, as shown in the Arrhenius plots in Extended Data Fig. 4. As the distance is reduced from 1.2 mm to 0.35 μm, there is a noticeable increase in the energy gap for the fractional filling factors 5/3, 7/5 and 4/3 within the second Landau level (Fig. 3d). It is important to note that these fractions are part of the Jain principal sequence²⁹ originating from the 1/3 Laughlin state. Although our highest magnetic field strength does not permit us to reach the filling factor ν = 2/3, we are able to achieve the fraction 4/5, which is associated with the 1/5 Laughlin state. The energy gap for the 4/5 fraction, observed in the lowest Landau level, does not increase significantly within the error bars. This suggests that the cavity-mediated effects may have contrasting impacts on the 1/3 and 1/5 families of fractional quantum Hall states. This behaviour is highlighted by extending the temperature analysis to a lower regime, in which the longitudinal resistivity ρ_xx follows a power law: ρ_xx = αT^γ. The decay rate γ shows consistent behaviour for the fractions 5/3, 7/5 and 4/3, increasing with coupling, whereas the fraction 4/5 remains unaffected (Fig. 3e). Although the activation energy of 5/3 and 7/5 has large errors, the corresponding error in γ is small enough to clearly indicate variations beyond the error margin. These two methods of analysis on the same dataset confirm the cavity’s effect on the fractions. A detailed discussion of the complete temperature analysis is provided in the Supplementary Information. It is important to note that this analysis does not aim to provide a more precise value for the activation gap, but rather to highlight, through a self-referenced investigation, the intricate effects of the cavity on various states within the quantum Hall system. Comparison with reference measurements on the same heterostructure in van der Pauw geometry in Extended Data Fig. 5 shows that activation energies in those samples almost double compared to those measured in our relatively narrow Hall bars. Such dependence is expected as it is generally observed that the quality of the fractional states decreases with sample area³⁵.

As fractional quantum Hall states arise solely from electron–electron interactions, these observations suggest that the cavity mediates an additional effective electron–electron interaction that competes with the Coulomb interaction. Such cavity-mediated interactions are also discernible at odd-integer filling factors, for which the activation energy gap is typically defined by spin splitting. In GaAs, this energy gap is predominantly influenced by the exchange splitting due to Coulomb interactions. The modifications in exchange splitting observed in our experiments also indicate the presence of a cavity-mediated potential.

To understand the cavity-mediated effects, we present here a simplified theoretical description for electrons subject to a perpendicular magnetic field and a single cavity mode (see the Supplementary Information for further details).

For the cavity mode, whose angular frequency is ω_cav and whose bosonic creation (annihilation) operator is \(\widehata^\dagger \) (\(\widehata\)), we assume a linearly polarized vector potential with a constant spatial gradient, namely \(\widehat\bfA^\rmcav(\widehat\bfr)=(A_\rmvac+\mathcalG_\rmA\,\widehaty)(\widehata+\widehata^\dagger )\bfe_y\). The gradient \(\mathcalG_\rmA\) is related to the gradient of the vacuum electric field through \(\mathcalG_\rmE=\omega _\rmcav\mathcalG_\rmA\). The quantum light–matter interaction consists of a paramagnetic contribution (linear in the photon operators) and a diamagnetic term (quadratic in the bosonic operators). The part of the Hamiltonian that depends on the photonic operators alone can be diagonalized through a Bogoliubov transformation in terms of the renormalized boson operator \(\widehat\alpha \) and cavity mode frequency \(\widetilde\omega _\rmcav\) (ref. ¹⁷).

If the cavity photon field is not resonant to the electronic transitions, we can adiabatically eliminate it and determine an effective electron–electron interaction within a given Landau band (Supplementary Information and D.B. et al., manuscript in preparation):

with \(\eta _m_1m_2=\sqrtm_1\sqrtm_1-1\sqrtm_2+1\sqrtm_2+2\) and \(\mathcalD=\left(\frac\omega _\rmcav\widetilde\omega _\rmcav\right)(\mathcalG_\rmA\ell )^2\left(\frace^22m_\star \right)\), in which \(\ell =\sqrt\hbar /eB\) is the magnetic length, −e is the electron’s charge, and m_⋆ is its effective mass. The fermionic operator \(\widehatc_m^\dagger \) creates an electron in the state with angular momentum m (symmetric gauge) in the considered Landau level (Fig. 4). For simplicity, we are omitting the spin index. Note that the spatial gradient is essential to create an intraband interaction.

Diagram representing the exchange of two angular momenta between distant electrons through the exchange of two cavity photons.

We have been able to calculate analytically the effect of \(\widehat\mathcalH_\rme-\rme^(\rmcav)\) on the exchange spin splitting at odd-integer filling factors and also on the modification of fractional quantum Hall gaps in the so-called single-mode approximation⁴². The cavity contribution to the exchange splitting is \(\langle \rmFP| \widehat\mathcalH_\rme-\rme^(\rmcav)| \rmFP\rangle \), in which \(| \rmFP\rangle =\widehatc_^\dagger \ldots \widehatc_N_\textdeg-1^\dagger | \rmvac\rangle \) is the fully packed state corresponding to an odd-integer filling factor. When the Landau degeneracy N_deg ≫ 1, we have \(\Delta E^\rmexc\simeq \langle \rmFP| \widehat\mathcalH_\rme-\rme^(\rmcav)| \rmFP\rangle \simeq \frac\mathcalD^212\hbar \widetilde\omega _\rmcavN_\textdeg^3\), in which \(N_\textdeg=\fracL_xL_y2\rm\pi \ell ^2\) with L_x and L_y being the spatial dimensions of the 2D sample. As the effective g-factor is dominated by Coulomb interactions, and the cavity-mediated potential is attractive, the cavity correction to g^⋆ (the absolute value of the g-factor) is hence negative:

in which μ_B is the electron Bohr magneton. Let us consider parameters corresponding to our experimental configuration, namely \(\widetilde\omega _\rmcav=7.5\times 1^11\,\rmrad\,\rms^-1\), a density of electrons n = 2 × 10¹¹ cm⁻², L_x = L_y = 100 × 10⁻⁶ m and B = 0.5 T, and with the spatial gradient of the vacuum electric field being \(\mathcalG_\rmE=4\times 1^8\,\rmV\rmm^-2\). With these values, we get Δg^⋆ ≃ −2, which is close to what is observed in the experiment.

To describe fractional quantum Hall states, for any two-body interaction that conserves angular momentum, the Haldane pseudo-potential components are key quantities²⁰. We have found the following long-range Haldane pseudo-potentials for the cavity-mediated interaction: \(v_m^\rm(cav)=\left(-\frac\mathcalD^28\hbar \widetilde\omega _\rmcav\right)(m^2-m)\). We remark that if only Coulomb interaction (\(v_m^(\rmC)\propto 1/\sqrtm\)) were present, its short-range component \(v_1^(\rmC)\) would be responsible for the FQH gap opening, whereas the long-range ones \(v_m > 1^(\rmC)\) would reduce the magnitude of the gap opened by \(v_1^(\rmC)\). Our cavity-mediated interaction, which is added on top of Coulomb interaction, leaves the short-range components unaffected, and decreases the long-range components; thus, an overall increase of the gap would not be unexpected (see Supplementary Information for exact diagonalization results).

An interaction potential corresponding to the cavity-mediated potential Haldane components \(v_m^(\rmcav)\) reads: \(V^(\rmcav)(r)\,=\)\(\left(-\frac\mathcalD^28\hbar \widetilde\omega _\rmcav\right)\left[\frac116\left(\fracr\ell \right)^4-\left(\fracr\ell \right)^2+2\right]\). Note that the divergence at large distances r is due to the approximation of considering a cavity mode with a constant spatial gradient \(\mathcalG_\rmE\). A cutoff at large distances is not only expected by the finite-size nature of the Hall bar but also due to the fact that the spatial region with large gradients is a fraction of the sample (Fig. 1). To evaluate the many-body gap of fractional quantum Hall states, a powerful technique is the Girvin–MacDonald–Platzman magneto-roton theory⁴², which assumes that the collective excitation gap can be determined by the sole knowledge of the (Laughlin) ground state. The Girvin–MacDonald–Platzman model is well known to faithfully capture the minimum of the composite-fermion exciton magneto-roton mode on top of the Laughlin states, giving an approximate lower bound for the large-k energy of this mode, which corresponds to the transport gap⁴³.

Considering the potential V^(cav)(r) provides a divergent result. We have regularized that by introducing an infrared cutoff due to the finite size of the sample.

The variation of the fractional quantum Hall gap due to the presence of the cavity reads

in which L is the length associated with the infrared cutoff (see Supplementary Information for more details). Note that, as in the case of the cavity-modified g-factor, the variation of the fractional quantum Hall gap scales with \(\mathcalD^2L^4\propto \mathcalG_\rmE^4N_\textdeg^2\), showing again the key role of the spatial gradient and the collective electron contribution due to the long-range nature of the perturbation. By taking L = 100 μm (roughly the system size) and spatial gradients of the same order as the ones used for the calculation of the exchange splitting, setting \(\ell k_\min =1.3\) and \(\overlines(k_\min )\approx 1\) (the values for the 1/3 Laughlin state⁴²), we get \(\frac\Delta ^(\rmcav+C)-\Delta ^(\rmC)\Delta ^(\rmC)\approx 0.5\), which is comparable to what we observed in our experiments. We remark that the states 4/3 and 5/3, in the absence of spin mixing and Landau level mixing, are the 1/3 state and its conjugate hole, 2/3, in the top Zeeman-split lowest Landau level. Although the already complex theory is based on many simplifications (single-mode cavity, constant spatial gradient of the vacuum electric field and magneto-roton theory for the excitation gap), the magnitude of the predictions is consistent with the experimental observations.

This joint experimental and theoretical study has demonstrated the capacity of electromagnetic vacuum fields with pronounced spatial gradients to control complex, strongly correlated electronic systems, specifically fractional quantum Hall phases. Notably, we observed a significant enhancement of fractional quantum Hall gaps within a key group of fractions. We have revealed that the exchange of virtual cavity photons can induce an effective attractive long-range electron–electron interaction, which competes with the Coulomb interaction. Additionally, we found that this cavity-mediated attractive interaction substantially reduces the exchange spin splitting, which is responsible for the activation energy gap at odd-integer filling factors.

These experimental results were achieved using a ‘hovering’ resonator technique. This method finely tunes the electromagnetic vacuum fields by adjusting the distance between the cavity and the Hall bar, offering precise control over the coupling strength. Moreover, this approach has broader implications and can be generalized to any 2D material and small planar quantum device. Specifically, leveraging cavity vacuum fields in this manner could manipulate strongly correlated phases in moiré materials, such as by stabilizing fractional Chern insulators^44,45,46 or altering superconductivity⁴⁷ properties, and may ultimately be implemented within quantum information processing purposes.

Note added in proof: While completing this manuscript, we became aware of a theoretical preprint focusing on the resonant hybridization of the magneto-roton with the cavity photon field⁴⁸.