Transitions in dynamical regime and neural mode during perceptual decisions

Experiments

Animals

The animal procedures described in this study were approved by the Princeton University Institutional Animal Care and Use Committee and were carried out according to the standards of the National Institutes of Health (NIH). Animals consisted of 16 adult, 6–24-month-old, male Long–Evans rats (Rattus norvegicus, Hilltop Lab Animals, Taconic) that were housed in Technoplast cages in pairs with a 12-h reversed light–dark cycle. All training and testing procedures were performed during the dark cycle. The rats had free access to food, but they had restricted access to water. The amount of water that the rats obtained daily was at least 3% of their body weight. Sample sizes were chosen on the basis of previous electrophysiological studies in rats^28,29. No blinding or randomization was performed.

Behavioural task

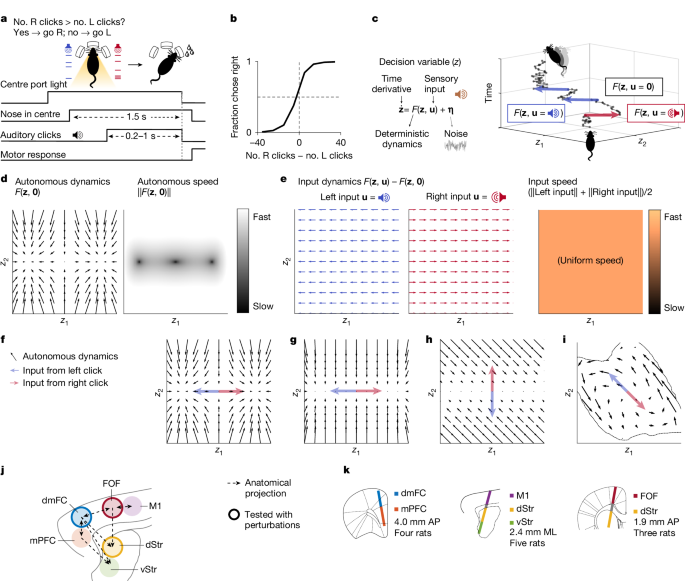
Rats performed the behavioural task in custom-made training enclosures (Island Motion) placed inside sound- and light-attenuated chambers (IAC Acoustics). Each enclosure consisted of three straight walls and one curved wall in which three nose ports were embedded (one in the centre and one on each side). Each nose port also contained one light-emitting diode that was used to deliver visual stimuli, and the front of the nose port was equipped with an infra-red beam to detect the entrance of the nose of the rat into the port. A loudspeaker was mounted above each of the side ports and used to present auditory stimuli. Each of the side ports also contained a silicone tube that was used for water reward delivery, with the amount of water controlled by valve-opening time.

Rats performed an auditory discrimination task in which optimal performance required the gradual accumulation of auditory clicks²⁴. At the start of each trial, rats inserted their nose in the central port and maintained this placement for 1.5 s (fixation period). After a variable delay of 0.5−1.3 s, two trains of randomly timed auditory clicks were presented simultaneously: one from the left speaker and one from the right speaker. At the beginning of each click train, a click was played simultaneously from the left and right speakers (stereoclick). Regardless of onset time, the click trains ended at the end of the fixation period, resulting in stimuli ranging from 0.2 s to 1 s. The train of clicks from each speaker was generated by an underlying Poisson process, with different click rates for each side. The combined mean click rate was fixed at 40 Hz, and trial difficulty was manipulated by varying the ratio of the generative click rate between the two sides. The generative click rate ratio varied from 39:1 (easiest) to 26:14 (most difficult) clicks per s. At the end of the fixation period, the rats could orient towards the nose port on the side where more clicks were played and obtain a water reward.

Psychometric functions were calculated by grouping the trials into eight bins of similar size according to the difference in the total number of right and left clicks and, for each group, computing the fraction of trials ending in a right choice. The CI of the fraction of right responses was computed using the Clopper–Pearson method.

Electrophysiological recording

Neurons were recorded using chronically implanted Neuropixels 1.0 probes that are recoverable after the experiment⁵⁰. In four animals, a probe was implanted at 4.0 mm anterior to the bregma and 1.0 mm lateral, for a distance of 4.2 mm, and at an angle of 10° relative to the sagittal plane that intersects the insertion site (the probe tip was more medial than the probe base). In five other animals, a probe was implanted to target M1, the dStr and the ventral striatum at the site 1.0 mm anterior and 2.4 mm lateral, for a distance of 8.4 mm, and at an angle of 15° relative to the coronal plane intersecting the insertion site (the probe tip was more anterior than the probe base). In a final set of three rats, a probe was implanted to target the FOF and anterior dStr at 1.9 mm anterior and 1.3 mm lateral, for a distance of 7.4 mm, and at an angle of −10° relative to the sagittal plane intersecting the insertion site (the probe tip was more lateral than the probe base). Spikes were sorted into clusters using Kilosort2 (ref. ⁵¹), and clusters were manually curated.

Muscimol inactivation

Infusion cannulas (Invivo1) were implanted bilaterally over the dmFC (4.0 mm AP, 1.2 mm ML) in three rats. After the animal recovered from surgery, the animal was anaesthetized, and, on alternate days, a 600-nl solution of either only saline or muscimol (up to 150 ng) was infused in each hemisphere. Half an hour after the animal woke up from anaesthesia, the animal was allowed to perform the behavioural task.

Retrograde tracing

To characterize anatomical inputs into the dStr, 50 nl of cholera toxin subunit B conjugate (Thermo Fisher Scientific) was injected into the dStr at 1.9 mm AP, 2.4 ML and 3.5 mm below the cortical surface. The animal was perfused 7 days after surgery.

Histology

The rat was fully anaesthetized with 0.4 ml ketamine (100 mg ml⁻¹) and 0.2 ml xylazine (100 mg ml⁻¹) intraperitoneally, followed by transcardial perfusion of 100 ml saline (0.9% NaCl, 0.3× PBS, pH 7.0 and 0.05 ml heparin at 10,000 USP units per ml) and finally transcardial perfusion of 250 ml of 10% formalin neutral buffered solution (Sigma, HT501128). The brain was removed and postfixed in 10% formalin solution for a minimum of 7 days. Sections (100 µm) were prepared on a Leica VT1200 S vibratome and mounted on Superfrost Plus glass slides (Fisher) with Fluoromount-G (SouthernBiotech) mounting solution and glass coverslips. Images were acquired on a Hamamatsu NanoZoomer under ×4 magnification.

Autonomous and input dynamics

The class of dynamical systems we study here is specified by

for some generic function F, with z the latent decision variable and u the external input to the system from the auditory clicks in the behavioural task. At each moment, there may be no click, a click from the left or a click from the right. When time is discretized to sufficiently short steps, u is one of three values:

We define the autonomous dynamics of the system as

and the average input dynamics as

and, specifically, the average left and right input dynamics as

The sum of autonomous dynamics and average input dynamics is equal to the expected value of \(\dot\bfz\) computed over the distribution p(u|z):

Figure 2c shows a plot of \(\dot\bfz_\rma\rmu\rmt\rmo\rmn\rmo\rmm\rmo\rmu\rms\), and Fig. 2e shows a plot of \(\dot\bfz_\overline\rmleft\) and \(\dot\bfz_\overline\rmright\). F(z, left) is defined as p(u = [1; 0]|z)F(z, [1; 0]) + (1 − p(u = [1; 0]|z))F(z, 0), and F(z, right) is defined as p(u = [0; 1]|z)F(z, [0; 1]) + (1 − p(u = [0; 1]|z))(F(z, 0).

Because p(u|z) = p(z|u)p(u)/p(z) and p(z) in general do not have an analytical form, we estimate p(u|z) numerically. To do this, we train FINDR²⁰ to learn F and generate click trains for 5,000 trials in a way that is similar to how clicks are generated for the task performed by our rats. Next, we simulate 5,000 latent trajectories from the learnt F and the generated click trains. We then bin the state space of z and ask, for a single bin, how many times the latent trajectories cross that bin in total and how many of the latent trajectories when crossing that bin had u = [1;0] (or u = [0;1]). That is, we estimate p(u = [1;0]|z) with \(\frac\rmNo.\; latent\; states\; with\,\bfu\,=\,[1;\,0]\,\textin\,\rmt\rmh\rme\,\rmb\rmi\rmn\,\rmt\rmh\rma\rmt\,\rmc\rmo\rmv\rme\rmr\rms\,\bfz\,\rmNo.\; latent\; states\; in\; the\; bin\; that\; covers\,\bfz\). For Fig. 2, because z is two dimensional, we use bins of eight-by-eight that cover the state space traversed by the 5,000 latent trajectories and weigh the flow arrows of the input dynamics with the estimated p(u|z). Similarly, for the background shading that quantifies the speed of input dynamics in Fig. 2, we use bins of 100-by-100 to estimate p(u|z) and apply a Gaussian filter with σ = 2 (in the units of the grid) to smooth the histogram. A similar procedure was performed for Extended Data Figs. 1 and 4 to estimate p(u|z) numerically.

Speed of autonomous and input dynamics

To compute the normalized difference in the speed of autonomous and input dynamics in Fig. 3c, similar to previous sections, we first generated latent trajectories from the learnt F for 5,000 different trials with generative click rate ratios used in our experiments with rats. Next, we computed the magnitude of the autonomous dynamics \(\parallel \dot\bfz_\rma\rmu\rmt\rmo\rmn\rmo\rmm\rmo\rmu\rms\parallel \) and the magnitude of the average input dynamics \((\parallel \dot\bfz_\bar\rml\rme\rmf\rmt\parallel +\parallel \dot\bfz_\bar\rmr\rmi\rmg\rmh\rmt\parallel )/2\) for each time point for each of the 5,000 trajectories and then averaged across the trajectories and across time periods defined in Fig. 3b to obtain Fig. 3c.

FINDR

Detailed descriptions are provided in ref. ²⁰. Briefly, to infer velocity vector fields (or flow fields) from the neural population spike trains, we used a sequential variational autoencoder called FINDR.

FINDR minimizes a linear combination of two losses: one for neural activity reconstruction (\(\mathcalL_1\)) and the other for vector field inference (\(\mathcalL_2\)). To reconstruct neural activity, FINDR uses a deep neural network G that takes the spike trains of N simultaneously recorded neurons y and the sensory click inputs u in a given trial to obtain the time derivative of the d-dimensional latent decision variable z:

Here, T is the number of time steps in a given trial, u_t is a two-dimensional vector representing the number of left and right clicks played in a time step (Δt = 0.01 s), y_t is an N-dimensional vector of the spike counts in a time step and η_t is noise drawn from N(0, ΔtΣ) in each time step. Σ is a d-dimensional diagonal matrix in which the diagonal elements need not be equal to each other. For each time step, FINDR infers the firing rates of N simultaneously recorded neurons r_t from z_t with

where softplus is a function approximating the firing rate–synaptic current relationship (f–I curve) of neurons, W is an N × d matrix representing the encoding weights and b_t is an N-dimensional vector representing the putatively decision-irrelevant baseline input. The baseline b_t is learnt before fitting FINDR using the procedure described in Baseline and in detail in the Supplementary Methods, section 1.2. The reconstruction loss is given by

For vector field inference, we parametrize the vector field F with a gated feedforward neural network^20,32:

F gives the discretized time derivative of z. We find the vector field F that captures the latent trajectories z inferred from G in equation (8) by minimizing

The total loss that is minimized by FINDR is

where c = 0.1 is a fixed hyperparameter (c = 0.0125 in Extended Data Fig. 1g). FINDR minimizes \(\mathcalL\) by using stochastic gradient descent to learn W, Σ, the parameters of the neural network representing F and the parameters of the neural network G. It can be shown that \(\mathcalL\) is an approximate upper bound on the marginal log likelihood of the data and that training FINDR this way is equivalent to performing inference and learning with a sequential auto-encoding variational Bayes algorithm that straightforwardly extends the standard auto-encoding variational Bayes algorithm⁵².

After training, we plot the vector field (that is, a grid of \(\dot\bfz\)) using the learnt F and generate FINDR-predicted neural responses using equation (9) and

Equation (14) is an Euler-discretized gated neural stochastic differential equation^20,32.

Parameters

The total number of free parameters P of the FINDR model is given by

P_W is the number of parameters in the encoding weight matrix W, the dimensions of which are the number of neurons N and latent dimensionality d. P_Σ is the parameter count in the diagonal covariance Σ of the additive Gaussian noise of the latent z. The number of parameters in the neural networks parametrizing F(P_F) and G(P_G) are separate hyperparameters. Here, \(x=\fracP_F-d+d^22d+3\).

Hyperparameters

The hyperparameters that were optimized (P_F, P_G and α) include the number of parameters of the network F(P_F), the number of parameters of the network G(P_G) and the learning rate α ∈ 10⁻², 10^–1.625, 10^−1.25, 10^−0.875, 10^−0.5. We identify the optimal values for these hyperparameters in a 3 × 3 × 5 = 45 grid search. The grid search was performed separately for each set of training data for each of five crossvalidation folds. In each training set, three-quarters of the trials were used to the optimize the parameters under a given set of hyperparameters and the remaining one-quarter was held out to evaluate the model performance for that set of hyperparameters. Test data were never used in the grid search.

Latent space transformation

Because the encoding weight matrix W is not constrained to semi-orthogonality and can take only any real values, different combinations of W and z_t can give rise to the same firing rate vector r_t, even when baseline b_t is fixed. To uniquely identify the latent trajectories (except for redundancy from rotations and reflections), after optimization, we linearly transformed the latent space z to \(\mathop\bfz\limits^ \sim \):

where S is a d × d diagonal matrix containing the singular values of W and V is a d × d matrix containing the right singular vectors

U is an N × d matrix containing the left singular vectors of W (where N is the number of neurons). In the space of \(\mathop\bfz\limits^ \sim \), the encoding weight matrix is a linear transformation that preserves angles and distances because U is semi-orthogonal and can only give rise to an isometry such as rotation and reflection.

To obtain meaningful axes for the transformed latent space \(\mathop\bfz\limits^ \sim \), we generate 5,000 different trajectories of \(\mathop\bfz\limits^ \sim \) in generative mode (that is, using F and Σ in equation (14) but not G) and perform PC analysis on the trajectories. The PCs were used to define the axes of the decision variable \(\mathop\bfz\limits^ \sim \). In the main text, the PC1 axis of \(\mathop\bfz\limits^ \sim \) was denoted as z₁ and the PC2 axis of \(\mathop\bfz\limits^ \sim \) was denoted as z₂. In all our analyses, the latent trajectories and vector fields inferred by FINDR are shown in the transformed latent space of \(\mathop\bfz\limits^ \sim \) and scaled such that the latent trajectories along PC1 lie between −1 and 1.

Sample zone

In Figs. 2 and 3, to focus on the portion of the inferred vector field that is used by the single-trial trajectories, we show only the well-sampled subregion of the state space, which is the portion occupied by at least 50 of 5,000 simulated single-trial latent trajectories of 1 s. With this definition, the sample zone is the same across time points in Fig. 2h.

Model evaluation

The goodness of fit of the PSTH was quantified using the coefficient of determination (R²) of the evidence–sign conditioned PSTH as defined in equation (34) using fivefold cross-validation. We used three-fifths of the trials in a session as the training dataset, one-fifth of the trials as the validation dataset to optimize the hyperparameters of FINDR and one-fifth of the trials as the test (that is, out-of-sample) dataset to evaluate performance of FINDR. Therefore, when we compute the goodness of fit, we also obtain five different vector fields inferred by FINDR for each fold, which we confirm are consistent across folds (Extended Data Fig. 4).

Curvature of trial-averaged trajectories

To compute the curvature of trial-averaged trajectories in Fig. 3b, as before, we first generate latent trajectories from FINDR for 5,000 different trials with generative click rate ratios used in our experiments with rats. Next, we separate the trials on the basis of whether the generative click ratio in a given trial favours a leftward choice or a rightward choice. We take the average of the latent trajectories over the left-favouring trials and then convolve the trial-averaged trajectory with a Gaussian filter with σ = 3 (in units of the time step Δt = 0.01 s). We take this smoothed trajectory to numerically compute the planar curvature. We do the same for the right-favouring trials and take the average between the curvature obtained from left-favouring trials and the curvature obtained from right-favouring trials to generate the plot in Fig. 3b.

cFINDR

The cFINDR model replaces the neural network parametrizing F in FINDR with a linear combination of affine dynamics, specified by M and N, and bistable attractor dynamics specified by φ. The dynamics are furthermore constrained to be two dimensional.

The matrix M implements a line attractor located at z₂ = 0. The inputs u_t are the same as those in FINDR and represent the auditory clicks. The two discrete attractors are constrained such that x₂ = 0 and implemented through the function φ. The shape of the basin of attraction corresponding to each point attractor is specified by the parameter ρ. The relative contribution of the discrete attractors and the line attractor to the overall dynamics is specified by the scalar s.

The DDM line attractor hypothesis can be implemented in cFINDR by setting θ = 0. Non-normal dynamics with a line attractor² can be implemented by setting θ ≠ 0. The bistable attractor hypothesis can be implemented by increasing ρ.

As in FINDR, cFINDR learns W, Σ and parameters of G. Instead of the neural networks parametrizing F, cFINDR, learns s, θ, r, x, ρ and the 2 × 2 matrix N to approximate F, which has nine parameters. The same objective function and optimization procedure were used in cFINDR. After optimization, as in FINDR, the latent space z is linearly transformed to uniquely identify the dynamics (except for arbitrary rotations or reflections). As in the analysis of results from FINDR, the latent trajectories and vector fields inferred by cFINDR are in the transformed latent space \(\mathop\bfz\limits^ \sim \).

When we fit cFINDR to the data, we experimented with the different constraints r > 0 and r > 3. The fits using r > 0 were superior to those using r > 3 and were therefore used in the comparison between cFINDR and FINDR for the data presented in Fig. 3e,f. We were motivated to try both r > 0 and r > 3 because we found that, in synthetic data, cFINDR under the constraint r > 0 could not recover the dynamics generated under the DDM line attractor hypothesis (r = 10). For this reason, Extended Data Fig. 5f shows results from synthetic data using r > 3. When fit to data, FINDR outperforms cFINDR using either r > 0 or r > 3.

FINDR models with more than two latent dimensions

For Extended Data Fig. 3j,k, we evaluated FINDR models with more than two latent dimensions to assess whether the two-dimensional manifold we found is approximately an attractor. To show that the sample zone was an approximate attractor manifold, we perturbed the latent states on the manifold along the third PC direction. When the latent states were perturbed (but not so far that the latent states went outside the range along the PC3 axis covered by the sample zone), the latent states flowed towards the manifold. To obtain the flow directions along PC3, we first generated 5,000 latent trajectories (similar to Fig. 2 for computing the sample zone). We then divided the PC1 × PC2 space into an eight-by-eight grid (the grid used for the vector field arrows in Extended Data Fig. 3i). For each cell in the grid, we identified the latent states from the 5,000 trajectories that were inside the cell and identified the highest (lowest) PC3 value \(z_3^\rmup(z_3^\rmdn)\). This was to ensure that the perturbation along the PC3 axis was not too large. Next, we computed the flow vector using a 100-by-100 grid on the PC1 × PC2 space, assuming that \(\rmPC3=z_3^\rmup(z_3^\rmdn)\) and PC4 = 0. The space covered by each cell of the grid is coloured on the basis of the direction of the flow vector along PC3: if flowing upwards, green; if flowing downwards, pink. A Gaussian filter was applied to this heat map with σ = 2 (in units of the 100-by-100 grid), similar to the heat map for input dynamics in Fig. 2f. The resulting plot is shown on the left (right) panel. Results were similar without the Gaussian filter.

Choice decoding from FINDR

FINDR does not use the choice of the animal for reconstructing neural activity. However, after training, we can fit a logistic regression model that predicts the choice of the animal from the decision variable z at the final time step T. When we fit an ℓ₂-regularized logistic regression model using z_T from the trained network G and the choice of the animal in the representative session in Fig. 2c–h, we found that the logistic choice decoder achieves 89.7% accuracy in predicting choice in the out-of-sample dataset. We can generate choices from this decoder by generating latent trajectories using F and Σ in equation (14) as in previous sections and by supplying z_T to the trained decoder. A total of 5,000 latent trajectories and choices generated from F and the choice decoder were used for the analysis in Extended Data Fig. 4l. We used a separate logistic regression model for predicting choice from the latent trajectories truncated at time = 0.33 s projected onto PC2. Optimization of the logistic regression models was carried out using L-BFGS⁵³.

MMDDM

The MMDDM is a state-space model, comprising a dynamic model that governs the time evolution of the probability distributions of latent (that is, hidden) states and measurement models that define the conditional distributions of observations (that is, emissions) given the latent state. Additional information is provided in the Supplementary Methods, section 1.3.

Dynamic model

The latent variable z is one dimensional (that is, a scalar), and its time evolution is governed by a piecewise linear function:

When the absolute value of z is less than the bound height B (free parameter), its time evolution depends on momentary external input u and i.i.d. (independent and identically distributed) Gaussian noise η.

where Δt is the time step and set to 0.01 s. Here, ~ means ‘distributed as’. When \(z\) is either less than −B or greater than B, it becomes fixed at the bound. The initial probability distribution of z is given by

where the mean µ₀ is a free parameter. In time step t, the input u(t) is the total difference in the per-click input v between the right and left clicks that occurred in the time interval (t − Δt, t):

where L(R) is the set of the left (right) click times and v(τ; t) is the per-click input of a click occurring at time τ and time step t. Note that \(\tau \in \mathbbR\) indicates continuous time, whereas \(t\in \mathbbN\) indexes a time step. The per-click input is given by

where D(τ; t) indicates the integral over the interval [t − Δt, t) of the Dirac delta function δ delayed by τ:

where ε is the machine epsilon. To account for sensory adaptation, the per-click input is depressed by preceding clicks by a time-varying scaling factor given by the function C(τ), implemented according to previous work²⁴ (Supplementary Methods, section 1.3.1). The per-click input is corrupted by i.i.d. multiplicative Gaussian noise ζ:

The free parameter \(\sigma _\rms^2\) is the variance of the per-click noise. Variability in the dynamic model is fit to the data through the per-click noise ζ rather than per-time step noise η on the basis of previous findings²⁴; our results are similar if we set the variance of η rather than the variance of ζ as a free parameter.

The dynamic model has three free parameters: bound height B, variance \(\sigma _\rms^2\) of the per-click noise and mean µ₀ of the initial state. These parameters are learnt simultaneously with the parameters of the measurement models.

Measurement model of behavioural choices

In each trial, the binary behavioural choice c (1, right; 0, left) is the sign of z in the last time step T of the trial (the earlier of 1 s after the onset of the clicks or immediately before the animal leaves the fixation port):

Measurement model of spike counts

In each time step t, given the value of z, the spike count y of neuron n is a Poisson random variable

The firing rate λ is given by

where \(h(\cdot )\) is the softplus function used to approximate the neuronal frequency–current curve of a neuron:

The encoding weight w depends on z itself:

Each neuron has two scalar weights, w_EA and w_DC, that specify the encoding of the latent variable during the evidence accumulation regime and the decision commitment regime, respectively. When the latent variable has not yet reached the bound (−B or B), all simultaneously recorded neurons are in the evidence accumulation regime and encode the latent variable through their own private w_EA. When the bound is reached, all neurons transition to the decision commitment regime and encode \(z\) through their own w_DC.

The bias b accounts for factors that are putatively independent of the decision, including a component that varies only across trials and another component that varies both across and within trials:

The cross-trial trial component \(b_\textcross^(n)\) is a function of time m from the first trial of the session, whereas t indicates time in each trial relative to the stimulus onset of that trial. The within-trial component consists of time-varying influence from spike history, post-stimulus (stim) onset and pre-movement (move) onset.

where the symbol \(\ast \) indicates convolution, τ_x indicates translation τ_xk(t) = k(t − τ_x) by the time of event x and δ is the Dirac delta function. The functions \(b_\textcross^(n),k_\textstim,k_\textmove,k_\textspike\) are learnt, and each is parametrized as a linear combination of radial basis functions^40,54 (Supplementary Methods, section 1.5). The measurement model of each neuron of the spike train has 19 parameters that are learnt simultaneously with the parameters of the dynamic model (that is, the model of the latent variable).

Parameter learning

All parameters, including the three parameters of the latent variable and the 19 parameters private to each neuron, are learnt simultaneously by jointly fitting to all spike trains and choices using maximum a posteriori estimation. Gaussian priors were placed on the model parameters to ensure that the optimization reached a critical point and confirmed to not change the results in separate optimizations using maximum likelihood estimation (that is, optimization without Gaussian priors). Out-of-sample predictions were computed using fivefold cross-validation.

nTc

The time step when decision commitment occurred is selected to be when the posterior probability of the latent variable at either the left bound or the right bound, given the click times, spike trains and behavioural choice, is greater than 0.8. Results were similar for other thresholds, and the threshold of 0.8 was chosen to balance between prediction accuracy and the number of trials for which commitment was predicted to have occurred. Using this definition, commitment occurred in 34.6% of trials.

Engagement index

The engagement index was computed for each neuron to quantify its involvement in evidence accumulation and decision commitment. The index was defined using w_EA and w_DC of the neuron: EI ≡ (|w_EA| − |w_DC|)/(|w_EA| + |w_DC|). It ranges from −1 to 1. A neuron with an engagement index of −1 encodes the latent variable only during decision commitment, an engagement index of 1 indicates involvement only during evidence accumulation, and an engagement index of 0 represents a similar strength of encoding the latent variable during evidence accumulation and decision commitment.

Analyses

Neuronal selection

Only neurons that meet a preselected threshold for being reliably choice selective were included for analysis. For each neuron, reliable choice selectivity was measured using the area under the receiver operating characteristic curve (auROC) indexing how well an ideal observer can classify between a left-choice trial and a right-choice trial on the basis of neuronal spike counts. Spikes were counted in four non-overlapping time windows (0.01–0.21 s, 0.21–0.4 s, 0.41–0.6 s and 0.61–0.9 s after stimulus onset), and an auROC was computed for each time window. A neuron with an auROC < 0.42 or an auROC > 0.58 for any of these windows was considered choice selective and included for other analyses. Moreover, neurons must have had an average firing rate of at least two spikes per s. Across sessions, the median fraction of neurons included under this criterion was 10.4%.

PSTH

Spike times were binned at 0.01 s and were included up to 1 s after the onset of the auditory stimulus (click trains) until 1 s after the stimulus onset or until the animal removed its nose from the central port, whichever came first. The time-varying firing rate of each neuron in each group of trials (that is, task condition) was estimated with a PSTH, which was computed by convolving the spike train on each trial with a causal Gaussian linear filter with a standard deviation of 0.1 s and a width of 0.3 s and averaging across trials. The CI of a PSTH was computed by bootstrapping across trials.

The goodness of fit of the model predictions of the PSTH was quantified using the coefficient of determination (R²), computed using fivefold crossvalidation. R² was computed by conditioning the PSTH on either the sign of the evidence (that is, whether the generative click ratio in a given trial favoured a leftward choice or a rightward choice) or the choice of the animal:

where t is time in a trial that goes from 0 s to 1 s, with 0 s being the stimulus onset. The superscripts ‘^R’ and ‘^L’ indicate either the sign of the difference in the total number of right and left clicks or the choice of the animal. The subscripts ‘_obs’ and ‘_pred’ indicate whether the PSTH was computed using observed neural activity or model-predicted neural activity. SS_res is the residual sum of squares, and SS_tot is the total sum of squares.

A normalized PSTH was computed by dividing the PSTH by the mean firing rate of the corresponding neuron across all time steps across all trials. When PSTHs were separated by ‘preferred’ and ‘null’, the preferred task condition was defined as the group of trials with the behavioural choice when the neuron responded more strongly and a null task condition was defined as the trials associated with the other choice.

Choice selectivity

In Fig. 6 and Extended Data Fig. 2m, for each neuron and for each time step t aligned to the onset of the auditory click trains, we computed choice selectivity c(t):

where r and l are the PSTHs computed from trials ending in a right choice and a left choice, respectively. The time step t* is the time of the maximum absolute difference:

In Extended Data Fig. 2m, neurons are sorted by the centre of mass of the absolute value of the choice selectivity of each neuron.

Baseline

In FINDR, cFINDR and MMDDM, the neuronal firing rate depends on a time-varying scalar baseline. In time step t of trial m, conditioned on the value of the latents in a given time step, the spike count y of each neuron is given by

where h is the softplus function and w is the encoding weight of the latent. The baseline b incorporates putatively decision-independent variables as input to the neural spike trains including slow drifts in firing rates across trials and faster changes in each trial that are aligned to either the time from stimulus onset or the time from the animal leaving the fixation port. The baseline is learnt using a Poisson generalized linear model fit separately to the spike counts of each neuron. Details are provided in the Supplementary Methods, section 1.2.

PCTH

In trials for which a time of decision commitment (nTc) could be inferred, the spike trains were aligned to the predicted time of commitment and then averaged across those trials. The trial average was then filtered with a causal Gaussian kernel with a standard deviation of 0.05 s. The PCTHs were averaged in each of three groups of neurons: (1) neurons that were similarly engaged in evidence accumulation and decision commitment; (2) neurons more strongly engaged in evidence accumulation; and (3) neurons more strongly engaged in decision commitment. Each neuron was assigned to one of these groups according to its engagement index. Neurons with \(-\frac13\le \rmEI < \frac13\) are considered to be similarly engaged in evidence accumulation and decision commitment, neurons with \(\rmEI\ge \frac13\) are considered to be more strongly engaged in evidence accumulation, and those with \(\rmEI < -\frac13\) are considered to be more strongly engaged in decision commitment.

For this analysis, we focused on only the 65 of 115 sessions for which the MMDDM improved the R² of the PSTHs and for which the inferred encoding weights were reliable across cross-validation folds (R² > 0.9). From this subset of sessions, there were 1,116 neurons similarly engaged in evidence accumulation and decision commitment, 414 neurons that were more engaged in decision decision commitment and 1,529 neurons that were more engaged in evidence accumulation.

To compute the shuffled PCTH, the predicted times of commitment were shuffled among only the trials in which commitment was detected. If the randomly assigned commitment time extended beyond the length of the trial, then the time of commitment was assigned to be the last time step of that trial.

Trial-averaged trajectories in neural state space

To measure trial-averaged dynamics in neural state space, we analysed PCs in a data matrix made by concatenating the PSTHs. The data matrix X has dimensions TC-by-N, where T is the number of time steps (T = 100), C is the number of task conditions (C = 2 for choice-conditioned PSTHs and C = 4 for PSTHs conditioned on both choice and evidence strength) and N is the number of neurons. The mean across rows is subtracted from X, and singular value decomposition is performed: \(USV^\top =X\). The principal axes correspond to the columns of the right singular matrix V, and the projections of the original data matrix X onto the principal axes correspond to the left singular matrix (U) multiplied by S, the rectangular diagonal matrix of singular values. The first two columns of the projections US are plotted as trajectories in neural state space.

Psychophysical kernel

Kernels were time locked to either nTc of each trial (Fig. 5d and Extended Data Fig. 7a–d) or the first click in each trial (Extended Data Fig. 7e–h). We extended the logistic regression model presented in ref. ⁵⁵ to include a lapse parameter (Supplementary Methods, section 1.4), and we confirmed that results were similar using generic logistic regression. A shuffling procedure was used to randomly permute the inferred time of commitment across trials without changing the behavioural choice and the times of the auditory clicks on each trial. In this randomly permuted sample, we selected trials for which the auditory stimuli were playing at least 0.2 s before and at least 0.2 s after the inferred time of commitment to compute the psychophysical kernel in the shuffled condition. For Fig. 5d, the prediction was generated using the MMDDM parameters that were fit to the data and the same set of trials in the data. For Extended Data Fig. 7, temporal basis functions were used to parametrize the kernel, and the optimal number and type of basis function were selected used crossvalidated model comparison.

Statistical tests

Binomial CIs were computed using the Clopper–Pearson method. All other CIs were computed with a bootstrapping procedure using the bias-corrected and accelerated percentile method⁵⁶. Unless otherwise specified, P values comparing medians were computed using a two-sided Wilcoxon rank-sum test, which tests the null hypothesis that two independent samples are from continuous distributions with equal medians against the alternative hypothesis that they are not.

Estimating the low-dimensional vector field without specifying a dynamical model

For Extended Data Fig. 10d, we estimated the low-dimensional velocity vector field for each session using a method that does not specify a dynamical model (model-free approach). To obtain the model-free vector field, we first estimated single-trial firing rates of individual neurons by binning the spike trains into bins of Δt = 10 ms and convolving the spike trains with a Gaussian of σ = 100 ms centred at 0. Results were similar for other values of σ around 100 ms. Next, for each neuron, we took the average across all trials in the session and subtracted this average from single-trial firing rate trajectories. These baseline-subtracted firing rate trajectories were then projected to the low-dimensional subspace spanned by the FINDR latent axes. We projected the estimated firing rates to the same subspace as FINDR to allow direct comparisons between the FINDR-inferred vector field and the model-free vector field.

We treated this low-dimensional projection of the baseline-subtracted firing rates as the latent trajectories in this model-free approach. To obtain velocity vector fields from the latent trajectories, we first estimated the instantaneous velocity \(\dot\bfz\) at time point t by computing \(\dot\bfz_t=(\bfz_t-\bfz_t-\Delta t)/\Delta t\) for all t for all latent trajectories. We then divided the two-dimensional latent space into an eight-by-eight grid. For each cell (i, j) from this eight-by-eight grid, we identified all states z_t from all trajectories that fell inside the cell (i, j). We took the corresponding \(\dot\bfz_t\) of the identified z_t values and took the average to compute the velocity for the cell (i, j). We computed velocity vectors for all 64 cells. To compare vector fields, we took the cosine similarity between the velocity vector for cell (i, j) from FINDR and the velocity vector for cell (i, j) from the model-free approach and took the mean of these cosine similarities, S_c(FINDR, model free). In computing S_c(FINDR, model free), only cells that had a number of states greater than 1% of the total number of states were included. When the number of states used to estimate the velocity vector was less than 1% of the total number of states, we considered that cell (i, j) to be outside the sample zone, analogous to the sample zone in Fig. 2.

To compare between a random vector field and the model-free vector field, we generated 1,000 random vector fields (with each of the 64 arrows in the eight-by-eight grid going in random directions) for each session and computed S_c(random, model free) for each random vector field.

For Extended Data Fig. 10e, we estimated the autonomous dynamics vector field around the origin as a model-free way of confirming our findings in Extended Data Fig. 10a. Similar to the method for Extended Data Fig. 10d, we convolved the spike trains with a Gaussian and projected the baseline-subtracted firing rate trajectories to the low-dimensional subspace spanned by the FINDR latent axes. However, to separate autonomous dynamics from input dynamics, we used a Gaussian with a smaller σ (20 ms), with a window size ±3σ around 0, and then excluded any \(\dot\bfz_t\pm 3\sigma \) with time t for which a click occurred from the estimation of the autonomous dynamics. When computing the average of (z_t − z_{t − Δt})/Δt for one of the five pie slices, we required z_{t − Δt} to be inside the pie slice. For all sessions, the circle had a radius of 0.2 (in units of z). To further ensure that we estimated the autonomous dynamics, when computing the average, we only considered the trajectories for which the number of left clicks was equal to the number of right clicks during the epoch when they were in the pie slice.

Inclusion and ethics statement

The animal procedures described in this study were approved by the Princeton University Institutional Animal Care and Use Committee.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.