Thermalization and criticality on an analogue–digital quantum simulator

Device details

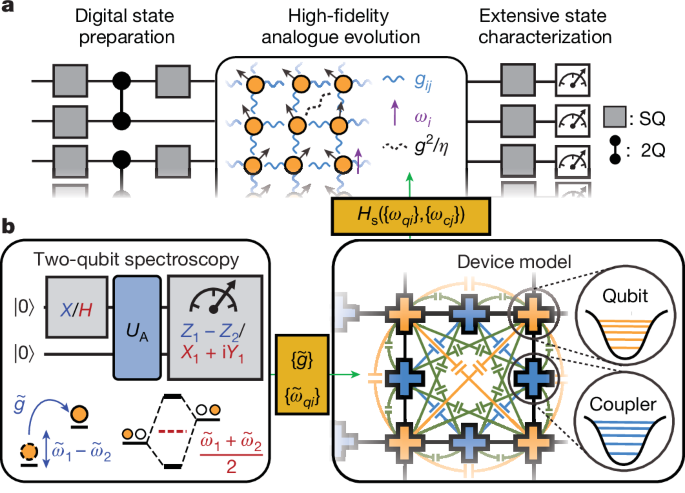
The experiments are performed on a superconducting quantum processor with frequency-tunable transmon qubits and couplers, with a similar design to that in ref. ⁴⁵. Extended Data Fig. 1a,b show the measured Ramsey dephasing (\(T_2^* \)) and photon relaxation (T₁) times at the interaction frequency of 5.93 GHz used in our experiments, with median values of 2.0 and 18.8 μs, respectively. Characterizing our digital gate performance, we find a median Pauli error of 4.5 × 10⁻³ for combined \(\sqrt\textiSWAP\,\) and single-qubit gates (Extended Data Fig. 1c), and 1.0 × 10⁻³ for single-qubit gates alone (Extended Data Fig. 1d). Finally, Extended Data Fig. 1e shows our readout errors, with a median of 1.4 × 10⁻².

Analogue calibration

In this section, we describe our new, scalable analogue calibration framework that enables roughly 0.1% cycle error per qubit. To achieve a scalable scheme, we perform pairwise calibration measurements—specifically single-photon and swap spectroscopy—which allows for accurately setting the effective coupling \(\widetildeg\) and dressed qubit frequencies \(\widetilde\omega _qi\) in each qubit pair. A key challenge in analogue calibration that contrasts with its digital counterpart is that these dressed quantities in the pairwise scenario change drastically when all couplers are turned on in the fully coupled global case. Therefore, we perform extensive modelling of the device physics to accurately convert them to the bare qubit and coupler frequencies, ω_qi,ω_cj, which, crucially, do not change from the local calibration measurements to the full-scale experiments.

Model device Hamiltonian

We model both the qubits and couplers in our tunable coupler architecture as Kerr oscillators, with four or five levels in each transmon, depending on the number of photons involved in the Hamiltonian term of interest. Specifically, in calculations concerning one- and two-photon terms, we include four and five levels, respectively. This is done to account for effects that do not obey the rotating-wave approximation, which couple \(| 1\rangle \) to \(| 3\rangle \) and \(| 2\rangle \) to \(| 4\rangle \). To ensure high accuracy, we account for not only coupling terms between neighbouring qubits and couplers, but also diagonal pathways, including between couplers:

where \(\widehatQ=a^\dagger +a\) and the \(\widetildek\) are the effective coupling efficiencies between transmons, including both direct and indirect capacitive contributions (note that the indirect contributions should not be confused with contributions due to virtual exchange interactions, which are included indirectly when we project out the couplers later on). The coupling efficiencies for the various terms can be summarized as follows:

For k_qq, we include three types of qubit–qubit coupling, distinguished by the relative positioning of the qubits. Notably, the geometry of the transmons breaks the 90° rotational symmetry; specifically, the couplings differ along the northwest–southeast (NW–SE) and northeast-southwest (NE–SW) directions. To discuss the three types of coupling, we consider the four qubits on a plaquette shown in Extended Data Fig. 2 and consider examples of pairs of transmons (the formulas for the remaining pairs are given by reflection symmetry about the NW–SE and NE–SW axes, for example, \(\widetildek_q_1,c_23=k_q_1,c_23+2k_q_1,q_2k_q_2,c_23\) infers that \(\widetildek_q_1,c_34=k_q_1,c_34+2k_q_1,q_4k_q_4,c_34\)):

1. (1)

   Nearest-neighbours qubits, q₁ and q₂ separated by a coupler c₁₂: \(\widetildek_q_1,q_2=k_q_1,q_2+k_q_1,ck_q_2,c\).

2. (2)

   Diagonally separated qubits in the NW–SE direction, q₁ and q₃: \(\widetildek_q_1,q_3=k_q_1,q_3+2(k_q_1,q_2k_q_2,q_3+k_q_1,q_4k_q_4,q_3)\).

3. (3)

   Diagonally separated qubits in the NE–SW direction, q₂ and q₄: \(\widetildek_q_2,q_4=k_q_2,q_4\).

For k_qc, we also include three types of qubit–coupler coupling:

1. (1)

   Nearest-neighbours: \(\widetildek_q_1,c_1=k_q_1,c_1\).

2. (2)

   Diagonally separated qubit and coupler in the NW–SE direction, q₁ and c₂₃: \(\widetildek_q_1,c_23=k_q_1,c_23+2k_q_1,q_2k_q_2,c_23\).

3. (3)

   Diagonally separated qubit and coupler in the NE–SW direction, q₄ and c₁₂: \(\widetildek_q_4,c_12=k_q_4,c_12\).

For k_cc, we consider two types of coupler–coupler coupling:

1. (1)

   Diagonally separated couplers in the NW–SE direction c₁₂ and c₂₃: \(\widetildek_c_12,c_23=k_c_12,c_23+2k_c_12,q_2k_q_2,c_23\).

2. (2)

   Diagonally separated qubit and coupler in the NE–SW direction, c₁₂ and c₁₄: \(\widetildek_c_12,c_14=k_c_12,c_14\).

Calibration experiments

To calibrate the bare qubit and coupler frequencies for a given set of applied biases, we perform various types of calibration measurements (Extended Data Fig. 3a):

Ramsey spectroscopy

In this measurement, we perform standard Ramsey spectroscopy for a range of applied qubit bias values, while keeping the couplers turned off and the neighbouring qubits detuned, to prevent swapping.

Swap spectroscopy

This measurement is performed on a pairwise level, in which neighbouring couplers (except the one connecting the pair) are turned off. The two qubits are prepared in the \(| 10\rangle \)-state and we measure the swap rate as a function of detuning between the two qubits (Extended Data Fig. 3b). The minimum swap rate tells us the effective coupling between the two qubits, \(\widetildeg\), and the detuning at which this occurs equals the difference between the dressed frequencies of the qubits, \(\widetilde\omega _q_1-\widetilde\omega _q_2\) (Extended Data Fig. 3c). Using an iterative scheme, we calibrate the coupler bias required to achieve the target effective coupling.

Single-photon spectroscopy

Whereas the swap spectroscopy provides us with the difference of the dressed frequencies, we also need to find their sum to determine the individual values, \(\widetilde\omega _q_1\) and \(\widetilde\omega _q_2\). We achieve this by preparing the qubits in \((| 1\rangle +| 0\rangle )| 0\rangle /\sqrt2\) and measuring ⟨X + iY⟩ as a function of evolution time (Extended Data Fig. 3d). The Fourier transform of the signal then reveals the eigenfrequencies of the two-qubit system, the average of which is equal to \((\widetilde\omega _q_1+\widetilde\omega _q_2)/2\) (Extended Data Fig. 3e).

Next, using separately calibrated coupling efficiencies, we model all the calibration experiments above with the device Hamiltonian described earlier, to find the bare qubit and coupler frequencies that give the dressed quantities observed in the calibration experiment. We model not only the two qubits and the coupler involved in pairwise experiments (single qubit involved in Ramsey), but also the neighbouring ‘padding’ qubits and couplers to account for their effects. Therefore, we start by determining the bare idle frequencies, ω^idle, because these must be known to represent the padding in the interaction configuration.

Projection onto computational subspace

Considering the fact that our model device Hamiltonian involves both qubits and couplers with up to five levels in each, it is computationally intractable to use it for time evolution even at small photon numbers. Moreover, in this form, it is very difficult to map its behaviour onto physically relevant systems. We therefore perform a projection technique to convert the device Hamiltonian into a spin Hamiltonian, H_s, that acts on the computational subspace. To find spin Hamiltonian terms involving n photons in a system of N_q qubits, we write \(H^(n)=\sum _i,j| i\rangle \langle i| H_\rmd| \,j\rangle \langle j| \), where \(\\) are our \(N_n=\left(\beginarraycN_\rmq\\ n\endarray\right)\) new dressed n-photon basis states.

Let us now motivate our choice of dressed basis states, by considering a few different options. One option could have been to simply use the bare qubit states, \(\ i\rangle _\rmbare\\); however, this would cause the spin Hamiltonian to have different eigen-energies from the low-energy spectrum of H_d. A second option would be to instead use the N_n lowest-energy n-photon eigenstates of \(H_\rmd,\ i\rangle _\rmeigen\\). In this case, the spin Hamiltonian is guaranteed to have the same N_n lowest n-photon eigen-energies as H_d. However, these basis states are highly delocalized and poorly represent our qubits. Hence, to get the best of both worlds, we turn to a third option, in which we project the bare qubit states onto the low-energy eigenspace spanned by \(\ i\rangle _\rmeigen\\). These projections are not orthonormal, so we perform singular value decomposition and set the singular values to one to arrive at our new dressed basis states. It can be shown that this is the most localized set of states that still preserve the low-energy eigenvalues⁵⁷. These new basis states are slightly delocalized on the nearest couplers and qubits, and also have a weak overlap with states that have n + 2 and n − 2 photons due to terms beyond the rotating-wave approximation. We note that our typical coupler ramp times of more than 5 ns are sufficient to ensure adiabatic conversion between the bare qubit states (in which we perform state preparation and measurement) and the dressed basis states that are relevant under analogue evolution.

The spin Hamiltonian H⁽ⁿ⁾ found from the technique above in principle includes all terms involving ≤n photons, including very long-range interactions; however, they drop off rapidly with the photon–photon separation d (typically as (g/η)^d ~ 0.1^d). Moreover, we also find that the terms decay with the number of involved photons in a similar way. Hence, to achieve the low error demonstrated in our manuscript, it is sufficient to include only terms involving up to two photons, and where all the involved qubits are a maximum Manhattan distance of two sites apart, resulting in:

where \(g_ij^nn,g_ijk^XnX\) and \(g_ijk^XIX\) scale as g²/η, while \(g_ijk^nXX\) scales as g³/η² and qubits i, j, k are connected (Extended Data Fig. 4). We note that there is an offset to these scaling behaviours, which arises due to the diagonal capacitive coupling. This is particularly evident for terms involving qubits along the NW–SE diagonal, because the diagonal coupling is strongest there.

Our technique requires finding the N_n lowest-energy n-photon eigenstates of H_d, which has a high computational cost for large N_q. Fortunately, for a given Hamiltonian term involving a certain set of qubits, the effect of other transmons decays quickly with distance, and we only need to include the nearest neighbouring qubits and couplers to achieve accuracies on the tens of kHz scale. To find the spin Hamiltonian terms, we therefore scan through various subsystems and perform the procedure outlined above for each of them.

Phase calibration for hybrid analogue–digital experiments

In experiments in which we prepare an entangled initial state, the frequency trajectories of the qubits lead to phase accumulation that must be characterized and corrected through phase gates, both before and after the analogue evolution (Extended Data Fig. 5a). Specifically, in the frame that rotates at the interaction frequency, the qubits in each dimer pair precess relative to each other before they reach the interaction frequency. Hence, a phase rotation ϕ_0,i must be applied to every qubit before turning on the analogue Hamiltonian to ensure that the dimer pairs have the desired phase difference when the coupling is turned on. Second, in the idle frame (in which we perform the final measurements) the qubits are precessing relative to each other while on resonance. Hence, a final phase correction ϕ_1,i + ω_it (where t is the analogue evolution time) must also be applied to every qubit before measurements. These corrections are very sensitive to timing and dispersive shifts: before the analogue evolution, a timing delay in dimer generation of only 150 ps corresponds to a 0.1-rad change in ϕ₀ for an idle frequency difference of 100 MHz. Furthermore, during the idle evolution, a 0.1% (80 kHz) change in dispersive shift leads to a 0.1-rad change in the final phase after 200 ns of analogue evolution. Hence, standard calibration techniques, such as single-qubit Ramsey spectroscopy, in which the configuration is sufficiently different from that in the actual experiment, are not accurate enough. We therefore use a set of three calibration techniques for ϕ_0,i, ϕ_1,i and ω_i that are designed to represent the configuration used in the actual experiment as well as possible:

To calibrate ϕ_0,i, we make use of the fact that the dimer state is only an eigenstate of the coupling Hamiltonian when the phase difference of the qubits is 0 or π. Hence, we sweep the phase difference and measure the population oscillations between the qubits with time. The correct phase compensation is the one that minimizes the amplitude of the population oscillations. We note two important points about this calibration step: first, as the measurements are in the Z-basis, they do not depend on the calibration of ϕ_1,i and ω_i. Second, because the phase calibrated in this step is accumulated before the couplers are turned on, it is not affected by dispersive shifts. It is therefore not a problem that neighbouring couplers are turned off during this particular step.

As mentioned previously, the calibration of ω_i is very sensitive to dispersive shifts and must therefore be performed in the exact same configuration as the actual experiment. We achieve this by performing the KZ experiment (ramp from Neel state in staggered field) with a slow ramp and leaving the analogue Hamiltonian on for a variable time (Extended Data Fig. 5d). The resultant state shows long-range XX + YY correlations, and the effect of the phase accumulation in the idle frame is to cause oscillations in the correlator between each pair i and j with a frequency ω_i − ω_j (Extended Data Fig. 5e). Hence, by measuring the frequency of oscillations of all the correlators, the full set of ω_i can be determined. The key advantage of this calibration measurement is that all the couplers are turned on, so that the dispersive shifts are the same as in the actual dimer experiment. However, the initial part of the KZ circuit—including the initial staggered field and the slow ramp of the couplers—is different, so the time-independent part of the phase correction, ϕ_1,i, must be calibrated separately.

Finally, to determine ϕ_1,i, we take advantage of energy conservation. Specifically, we perform the dimer experiment with single dimers while sweeping their final phase difference (Extended Data Fig. 5f). Only the correct phase compensation leads to ⟨X₁X₂⟩ = 1 and conserved energy, as can be see in Extended Data Fig. 5g. Whereas the dispersive shifts from neighbouring couplers affect the time-dependent part of the final phase ω_it and thus had to be included in the previous step, they do not have this effect on ϕ_1,i and can therefore be excluded here.

Finally, we note that for experiments not involving entangled initial states (Figs. 3 and 4), only the step for calibration of ω_i outlined above is required.

Readout correction and postselection schemes

Bell measurements

When measuring ⟨XX + YY⟩ correlators using standard single-qubit measurements, we cannot simultaneously get information about the number of photons measured on the pair of qubits, preventing us from postselecting our data on photon conservation. To get around this for nearest-neighbour pairs, we change our measurement basis by applying an entangling gate given by the unitary,

to each pair. From these measurements, we can deduce both the nearest-neighbour correlators and the number of photons present. We use this technique to process the data labelled ‘Bell’ in Fig. 3b. We find good alignment between direct measurements of the correlators and the inferred correlators from the Bell measurements.

Bell measurements with readout corrections

Typically, one can correct for readout errors by inverting the error channel. In the case in which readout errors are uncorrelated, we can simply characterize the matrix β for each qubit

where p_(i∣j) is the probability of measuring a state \(| i\rangle \) given that \(| \,j\rangle \) was prepared⁵⁸. In the case in which readout errors are correlated for pairs, we can similarly characterize a matrix γ for each pair

where p_(ij∣ab) is the probability of measuring a state \(| ij\rangle \) given that \(| ab\rangle \) was prepared. One can compensate for the effects of readout errors on an observable by inverting these matrices and applying them to the measured distribution of bitstrings of the subsystem involved in the observable.

In a case in which we want to both correct for readout errors and postselect our data, we cannot apply the readout correction on the postselected distributions as this would overcorrect for p_(0∣1) type errors. We also cannot simply correct the distributions of subsystem bitstrings before the postselection process because we need access to the global bitstrings to postselect on photon number conservation. Instead, we use a Markov-like process in which we consider each individual bitstring, and flip pairs of spins according to the probabilities inferred from the γ matrices. We then postselect the individual bitstrings on the criteria of photon conservation and, finally, compute the quantity of interest.

To confirm the validity of this method, we classically simulate a low-temperature state of the XY model for 64 qubits (using the ground state of two disconnected sets of 32 qubits), introduce noise to the system and use the above protocol to correct for the T₁ and readout errors. In simulating the readout errors, we include a readout bias equal to that observed in experiment, namely p_(0∣1)/p_(1∣0) = 3.7. We compute the energies of the system after various correction schemes and compare to the noiseless value. The results from these simulations are shown in Extended Data Fig. 6a,b, where we evaluate the performance for a wide range of readout error and probability of photon decay, respectively. The combined technique described above is found to provide the most accurate estimate of the actual energy across a very wide parameter range, extending beyond the range relevant to our experiment (in the experiment, we have readout errors in the range 1–4% and a probability of photon decay of 3–6% for ramp times of 200–500 ns). For very high T₁ errors, we find that the error in the combined technique eventually becomes slightly higher than that of pure postselection. In the special case of very low T₁ errors, we observe an interesting effect that leads to a slight underestimate of the energy, which can be understood as follows. Whereas the stochastic compensation of readout errors perfectly re-establishes the correct distributions of subsystem bitstrings (by construction of the probabilities with which we change the two-qubit bitstrings), each individual global bitstring has a non-zero probability of having the wrong total number of photons, even in the case of zero T1 error. The lowest-energy two-qubit state, \(| 10\rangle -| 01\rangle \) (converted to \(| 10\rangle \) by Bell conversion) has a slightly higher chance of being postselected than other two-qubit states. The result of this is a slight underestimate of the energy, which we emphasize is very small (roughly 1%) and not relevant in the parameter range of our experiment.

Comparison of ⟨X
X⟩ and ⟨Y
Y⟩

The final states produced after the ramp procedures in Figs. 3 and 4 are expected to be U(1)-symmetric, and thus have equally strong XX and YY correlations. We here check this by comparing ⟨XX⟩ and ⟨YY⟩ averaged over all nearest-neighbour qubit pairs across a range of ramp times (Extended Data Fig. 7), and indeed find that the two are equal.

Diffusion model

In Fig. 5h, we fit the observed energy transport with a diffusion model, which we describe in further detail here. We define the energy density at site (i, j), e_i,j(t), as the average of the energy (⟨XX + YY⟩/2) on the bonds that include site (i, j) and model the transport using a simple discretized version of the diffusion equation:

where the diffusion constant, D, is the only fit parameter.

Measurements of energy density fluctuations

We use measurements of two- and four-qubit correlators to reconstruct the energy density fluctuations, \(\sigma _\varepsilon =(n_\rmBg_\rmm)^-1\sqrt\langle H_XY^2\rangle -\langle H_XY\rangle ^2\), with:

where ⟨i, j⟩, ⟨j, k⟩ and ⟨m, n⟩ are nearest-neighbour pairs and i, j, k, m, n are distinct (note that j is included in the last sum to count the number of length-2 paths from i to k). Almost all of these terms can be reconstructed from just three different sets of measurements, namely X_i, Y_i and Z_i, except the four-qubit correlators involving both X and Y. To determine these, we measure eight periodic patterns of X, Y shown in Extended Data Fig. 8a, and leverage the substantial degree of isotropy to find the remaining correlators not included in these patterns (further justification below). As shown in Extended Data Fig. 8b, the four-qubit correlators that involve both X and Y show a clear trend with the distance between the centres of mass of the two involved nearest-neighbour pairs (i, j) and (m, n), and we therefore interpolate the data obtained from these eight sets of measurements to find the remaining terms. Determining σ_ε with good relative accuracy is challenging, owing to the very small relative difference between \(\langle H_XY\rangle ^2\) and \(\langle H_XY^2\rangle \). Nevertheless, we find that our technique works well, and we obtain relatively good agreement with MPS simulations (Extended Data Fig. 8c).

To further justify the use of this interpolation technique, we show the dependence of ⟨X_iX_jY_mY_n⟩ on the relative position of the centres of mass of the two involved nearest-neighbour pairs (i, j) and (m, n), showing near-isotropic distributions (Extended Data Fig. 9a). We observe a weak angular dependence with a period of π (Extended Data Fig. 9b), which becomes most pronounced when the correlation length is maximized (for example, g_mt_r = 12.3). The amplitude is only roughly ±0.01 (or roughly 5% of the signal itself) and is expected to be due to the system shape. As we are only interested in the sum of all the correlators, this small degree of isotropy has very little effect on the interpolation scheme described above. In Extended Data Fig. 9c, we compare the result of radial interpolation of ⟨XXYY⟩ at distance 5 (dashed black curve) to the actual correlators (coloured circles in main) and their average (red dashed curve in inset), and find that the difference is very small. In particular, we quantify the relative difference between the radial interpolation and the averaged actual correlators in Extended Data Fig. 9d, and find that it is on the order of a few percent, and even smaller at the long times that are most essential to our conclusions. These deviations are comparable to the statistical noise (as shown by the error bars) and do not contribute a dominant effect to the total energy fluctuations.

Correlation fitting

We here provide further details about the fitting procedures used in the main text for analysing correlations. As shown in Extended Data Fig. 10 and also in some of the curves in Fig. 3d, we observe distortions in the correlation decay at longer distances both in experiment (a) and simulation (b), which are expected to be due to the finite size of our system. Specifically, we find that the correlations drop rapidly for some ramp times and start increasing at others. If fitting up to the longest distances, these effects have a strong impact on the analysis, as can be seen from the sharp upturn in the fit error as we exceed a fit range of roughly six sites in Extended Data Fig. 10c. Informed by these findings, and the fact that the maximum distance at which such effects are still minimal is six sites, we use this as the fit-range cut-off. Note that we also observe a noise floor in the correlations around 10⁻², and we therefore do not fit data points smaller than this value.

We investigate the dependence on fit range further by plotting the r.m.s. fit errors for all ramp times and a wide range of fit-range cut-offs in Extended Data Fig. 10d,e (power-law and exponential fits, respectively). From these plots, it is again evident that the fits with distance cut-offs longer than six sites have particularly high errors (it is of course natural to see some increase in error with increasing fit range, but we are here referring to the distinct increase seen especially well in the inset of Extended Data Fig. 10d). Plotting the error ratio in Extended Data Fig. 10f, we find that all fits up to a fit range of seven sites show the same drop below one around g_mt_r = 10, and the discrepancy from KZ scaling is observed for all fit ranges (Extended Data Fig. 10g).