Analysis of GRAIL data
We analysed the PM and XM data from the GRAIL mission. The PM phase started on 1 March 2012 and ended on 29 May 2012 (that is, 89 days) with the average altitude of roughly 55 km (ref. 5). The XM phase started on 30 August 2012 and ended on 14 December 2012 (that is, 106 days) with the average altitude of roughly 23 km (ref. 6). The lower XM altitude was a key to improving the accuracy and resolution of the Moon’s static gravity field that resulted in the recovery of gravitational tidal Love numbers.
In our analysis, both PM and XM phases were divided into arcs of 2–3 days for data processing on basis of the spacecraft desaturation manoeuvre times for attitude control, so there is no thrusting during each data arc to minimize the non-gravitational errors on gravity field and Love number estimates. GRAIL’s primary dataset is the high-precision Ka-band range rate (KBRR) (32 GHz) and measurements were acquired through the onboard Lunar Gravity Ranging System56. The PM phase had a total of 39 arcs, and used 5-s sampled KBRR inter-satellite data and several DSN passes of two-way S-band data. The XM phase had a total of 58 arcs and used 2-s sampled KBRR data and several passes of the DSN two-way S-band data. Note that the KBRR is primarily used for determining the gravity field and in-plane spacecraft motion, whereas the DSN two-way S-band data are mainly used for determining the inertial orbit plane of the spacecraft, enabling absolute orbit positioning for GRAIL orbiters.
The separation distance between GRAIL orbiters varied linearly from 80 to 220 km near 1 April and then drifted back linearly to 80 km. This variation was designed to minimize error increases in the harmonic degrees that are in resonance with the separation distance57. The separation distance during XM was much smaller than the PM, ranging from 30 to 75 km, with an average of 60 km, to avoid potential multipath reflections.
Recovery of lunar gravity field GL1800F
The gravitational field potential, \(U(r,\lambda ,\phi )\), associated with the Moon is expressed as a spherical harmonic expansion17,58:
$$U(r,\lambda ,\phi )=\frac\rmGMr\mathop\sum \limits_l=0^\infty \mathop\sum \limits_m=0^l\left(\fracRr\right)^l\barP_lm(\sin \phi )[\barC_lm\cos (m\lambda )+\barS_lm\sin (m\lambda )],$$
(1)
where GM is the mass parameter of the Moon, l is the spherical harmonic degree, m is the order, \(\barP_lm\) are the normalized associated Legendre polynomials, \(\barC_lm\) and \(\barS_lm\) are the normalized spherical harmonic coefficients, R is the reference radius of Moon (1,738 km), λ is longitude, ϕ is latitude and r is the radius evaluated at the spacecraft position relative to a moon’s body-fixed frame. In this formulation, zonal coefficients are defined as \(\barJ_l=-\barC_l0\). The gravity field is modelled in the lunar principal axis frame1. As we are assuming that the origin of the Moon’s body-fixed frame is defined to be the Moon’s COM, the degree-1 coefficients are identically zero. The unnormalized spherical harmonic coefficients, \((C_lm,S_lm)\), are related to the normalized spherical harmonic coefficients as follows: \((\barC_lm,\barS_lm)=(C_lm,S_lm)/N_lm\), where the normalization factor \(N_lm\) is defined as:
$$N_lm=\sqrt\frac(l-m)!(2-\delta _0m)(2l+1)(l+m)!.$$
(2)
The Moon’s tidal gravity field is modelled as corrections to the spherical harmonic coefficients59,60,61:
$$\Delta C_lm-\rmi\Delta S_lm=\frack_lm2l+1\sum _j\frac\rmGM_j\rmGM\fracR^l+1r_j^l+1P_lm(\sin \phi _j)\rme^-\rmim\lambda _j,$$
(3)
where GMj is the mass parameter of body j and \((\lambda _j,\phi _j,r_j)\) represents the longitude, latitude and distance of the body j in the lunar body-fixed frame5,17. Equation (3) accounts for Earth–Moon tides, where j = 1 arises from both the Moon’s orbital eccentricity and its fixed roughly 6.7° obliquity around the Earth, as well as j = 2 for the Sun–Moon tides. The Sun–Moon tides generate forcing potentials that are roughly 5–10 times and 1,000 times smaller than the Earth–Moon tides at l = 2 and l = 3, respectively, and act over a shorter period. Moreover, for a laterally heterogeneous Moon, combinations of Sun–Moon and Earth–Moon tides induce temporal changes in the k3m based on equation (3). However, these variations are 2–3 times smaller than the effective uncertainties in k3m derived from gravity field inversions (Table 1) and are, therefore, disregarded in our analysis.
The gravity field of the Moon is usually determined by means of a least-squares estimation technique62,63. Several lunar gravity models have been delivered previously using least-squares estimation, with varying resolutions5,6,7,8,22,23,24. Achieving a high-resolution gravity field is important for improving the spatial resolution, as well as for improving the long-wavelength spectrums of the gravity, in particular l = 2 and l = 3, which are important for computing the lunar moments of inertia10 and gravitational tidal Love numbers k2m and k3m (refs. 5,7). Considering the intrinsic data quality and the ground track coverage, we recover a degree-1,800 field called GL1800F, which takes out almost all of the available gravity signatures with the full wavelength surface resolution of 6 km (that is, roughly 2πR/l).
The gravity field estimation is typically a two-step process64,65,66,67. First, the trajectory of each arc is computed through an orbit determination process by estimating the arc-dependent parameters, such as spacecraft initial states and non-gravitational periodic accelerations to account for spacecraft thermal radiation forces. Specifically, estimated arc-dependent (that is, local) parameters are the spacecraft state (unconstrained), three solar pressure scale factors (along the spacecraft–Sun direction at 1 and 0.1% for the two other normal directions) and 15 periodic acceleration coefficients per spacecraft in radial, transverse and normal directions every orbit (roughly 2 h). The a priori uncertainties of the periodic accelerations (constant, once-per-rev, twice-per-rev) depend on the spacecraft orbit geometry relative to the Sun (fig. 17 of ref. 57). The maximum initial uncertainties are at 1 × 10−12 km s−2 for orbits with the most lunar shadowing and a minimum of 3 × 10−14 km s−2 for the spacecraft always in full Sun. Also, during full Sun, radial components are removed, as well as twice-per-rev for the other two directions. The weighting scheme used for the GL1800F solution was identical to the weight scheme used for the GL0900D solution6. For the PM arcs, the 5-s KBRR data were weighted at 30 nm s−1, except for 19-MAY-2012 and 22-MAY-2012 arcs that were weighted at 60 nm s−1 due to signal multipaths off the lunar surface. For the XM arcs, the 2-s KBRR data were weighted at 50 nm s−1. The two-way DSN S-band Doppler data were weighted at 0.1 mm s−1. These weight values provide for correct scaling of the gravity field uncertainties for n > 100 based on differences of gravity solutions (for example, GL1800F and GL1500E). The second step involves solving for the global parameters, such as the gravity field, that are common to all arcs. For GL1800F, the estimated global parameters were Moon’s degree-1,800 gravity field, gravitational tidal Love numbers k2m and k3m, and the amplitudes of monthly periodic lunar core parameters. More details of least-squares estimation technique and filter setup are presented in the simulation results57 and the PM results5,7.
Computing a degree-1,800 field involves solving for roughly 3.24 million parameters. This is an extremely intensive numerical problem and requires careful implementation of generating partial derivatives, packing square-root information filter arrays, and inverting the resulting 39-TB upper-triangular square-root information filter matrix. The computation of GL1800F was done on NASA Ames Pleiades Supercomputers using 700 Haswell nodes, which has 20 cores with 128 GB of memory per node.
The resulting GL1800F almost completely flattens the postfit residuals of all the KBRR and DSN data, indicating that almost all gravity signatures are taken out from the available GRAIL data. The root-mean-square (r.m.s.) values of the KBRR residuals are shown in Extended Data Fig. 6. The postfit residuals of PM’s 5-s KBRR data have an average r.m.s. of about 35 nm s−1, with a minimum of 27 nm s−1 for the 17-MAY-2012 arc and the postfit residuals of XM’s 2-s KBRR data have an average r.m.s. of about 65 nm s−1. The overall noise characteristic of the KBRR data is mostly dominated by the Lunar Gravity Ranging System’s thermal noise. Compared to GL900D (ref. 6), the postfit residuals have improved everywhere, including a factor of 28 improvement for the 08-DEC-2012 arc in the last month of the XM. A few arcs during the last 2 weeks of the XM show the postfit residuals of about 40 nm s−1, which is much less than postfit residuals of the earlier phase of the XM. This is because the separation distance was much less for these periods, yielding a much higher signal-to-ratio for the KBRR data. The postfit residuals of both PM and XM’s 10-s DSN S-band data have an average of roughly 0.1 mm s−1, which is good compared to other planetary orbiters, due to the close Earth-to-Moon distance and the high-accuracy Earth media calibrations available from the DSN.
Processing GRAIL data requires a background model for the Moon’s orbit and orientation. We used the JPL’s Development Ephemeris (DE) series, which provides the time series of the ephemeris and orientation of the Moon. In this study, we considered both DE430 (ref. 21) and DE440 (ref. 1), which are based on the GRAIL-derived lunar gravity field. DE440 includes seven more years of lunar laser ranging data and an improved lunar gravity model1.
The gravity field coefficients for a degree-1,800 solution require a constraint of some type; without one, the coefficients become unrealistically large. Previous solutions, for example, used a power law constraint for part of the spectrum with l > 600 (GL0900D)6 or a topographic rank minus one (RM1) constraint23. We first computed an unconstrained degree-1,800 solution based on DE430, and another degree-1,800 solution was then computed by applying a different topographic constraint for l > 600 (also based on DE430). In this constraint, the a priori values of the spherical harmonic gravity coefficients are given by the gravity field coefficients determined from topography expanded to the 23rd power (ref. 68) with increasing density with depth. This is accomplished by first computing a constant density gravity from topography \([\rmGT(\rho _)]\) and then secondly by scaling the coefficients of each harmonic degree to the effective density for that given degree \((\rmGT_l=(\rho _l/\rho _)\rmGT(\rho _))\). The density versus degree was determined with a power law fit of the effective density from degrees 200 to 600 and then extrapolated to a density of 2,200 kg m−3 at degree 1,800 (Extended Data Fig. 3a,b, orange line). The a priori uncertainty of the constrained gravity harmonic coefficients were assumed to be 30% of the a priori values. The constraint is applied to smooth the coefficients over the areas where the solution is not as well determined. Using this constrained degree-1,800 gravity field as the background model, the GL1800F was computed by estimating degree-1200 spherical harmonic coefficients using DE440. This partial solution update was done to use the latest-available lunar orbit and orientation model and to avoid recomputation of a full degree-1,800 solution. The GL1800F solution is JPL’s first public release of a degree-1,800 lunar gravity field and is the highest resolution lunar gravity field published thus far (full wavelength surface resolution of 6 km).
The GL1800F gravity field is tied to the DE440 lunar orientation and is derived in the lunar principal axis frame. To be consistent with lunar cartographic products, GL1800F is also available in the mean-Earth frame. As the rotation from the principal axis-to-mean-Earth frame is defined as a fixed rotation1, the most straightforward way of computing the lunar gravity field in the mean-Earth frame is simply rotating the PA-based gravity field to the mean-Earth frame. This was accomplished with the available SHTOOLS software69. The 3–2–3 Euler rotation angles are:
(179.766217602292°, 0.021840987056123°, −179.785033451244°) for DE430,
(179.778382756033°, 0.0218596924458581°, −179.797230715235°) for DE440.
Both the GL1800F gravity field in the principal axis and mean-Earth frames are available through NASA’s Planetary Data System, and they are equivalent at the numerical noise level. For the Moon, the mean-Earth system is recognized as the international standard for lunar surface coordinates, as recommended by the International Astronomical Union’s Working Group on Cartographic Coordinates and Rotational Elements70. For tracking features on the lunar surface using cartographic products, such as surface mapping and optical or terrain-relative navigation, using the mean-Earth frame is therefore strongly recommended71.
Extended Data Fig. 3c,d show the r.m.s. gravity spectrum and errors of the constrained and unconstrained GL1800F solutions. The gravity spectrum shows a significant improvement of GL1800F (green) over GL0900D (blue) and GL1500E (orange). The constraint of the higher degrees of the lunar gravity field to within 30% of their expected values on the basis of topography gives similar results to previous RM1 solutions, although with a tighter λ = 10 constraint (fig. 9 in ref. 23). The Bouguer spectrum of GL1800F (cyan) crosses its error spectrum (green) at about l = 850, indicating that the solution is on average accurate to about l = 850. The independent solution GRGM1200B with λ = 1.0 (ref. 23) is also shown for comparison (yellow). Extended Data Fig. 3e,f show the correlations of gravity with gravity from topography for GL0900D, GL1500E, GRGM1200B and GL1800F, as well as the unconstrained GL1800F solution for comparison. Similar to the gravity spectrum, the correlation of GL1800F is significantly higher for l > 600 over GL0900D and GL1500E because of the topographic constraint.
Extended Data Fig. 7 shows the surface radial acceleration (positive downwards) of the lunar gravity field GL1800F solution projected onto the reference sphere of 1,738 km for the harmonic coefficients truncated at degree 600, excluding \(\overlineJ_2\) (maximum, 1,676 milliGal (mGal, unit of acceleration); minimum, −930 mGal). Extended Data Fig. 7a shows the Mollweide projection, Extended Data Fig. 7b shows the stereo projection of the northern hemisphere for 90° to 0° latitude and Extended Data Fig. 7c shows the stereo projection of the southern hemisphere for −90° to 0° latitude. Extended Data Fig. 8 shows the Bouguer gravity anomaly map of the lunar gravity field GL1800F solution projected onto the reference sphere of 1,738 km for the harmonic coefficients truncated at degree 600 (maximum 715 mGal, minimum −440 mGal). The Bouguer map was computed by differencing the surface radial acceleration of GL1800F and the gravity from topography, which was computed using the density of 2,372 kg m−3 for harmonic coefficients up to l = 600, whereas the extrapolated effective density curve (orange) was used for coefficients l > 600. Extended Data Fig. 8a shows the Mollweide projection, Extended Data Fig. 8b shows the stereo projection of the northern hemisphere for 90° to 0° latitude and Extended Data Fig. 8c shows the stereo projection of the southern hemisphere for −90° to 0° latitude.
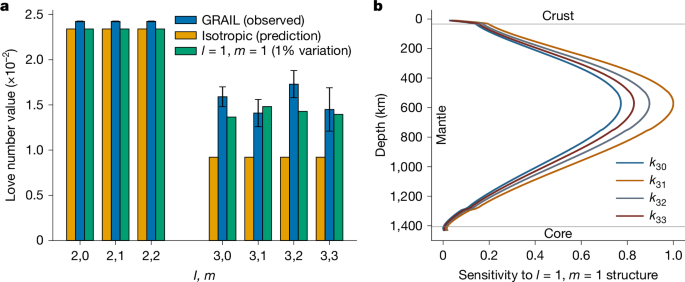
The nominal GL1800F includes k2m and k3 and their recovered values are shown in Table 1, showing when k3 = k3m, the recovered k3 = 0.0163 ± 0.0007 (that is, case 1). Compared to the k3 value expected for a spherically symmetric Moon (that is, k3 = 0.00945)10,27, our estimated k3 is about 72% larger. Extended Data Fig. 9 shows the variability of k3 per arc, where each arc is 2–3 days long. In these solutions, all the local parameters (for example, spacecraft state, solar pressure scale factors, non-gravitational period accelerations) are estimated together with k3 for each arc assuming the same data weights as mentioned above and with GL1800F as the nominal gravity field. The blue points show the k3 solutions for all PM arcs. During April and October, the GRAIL spacecraft were not occulted by the Moon when observed from the Sun, thereby minimizing non-gravitational forces, as indicated by the a priori constraint values mentioned above. Thus, during this period, the large k3 value is clearly recovered. The data from September, November and December are not shown because of the strong non-gravitational effects due to low spacecraft altitude and going through shadows. Table 1 also shows individual k3m when values at each order are estimated independently (that is, case 2). We have analysed the sensitivity to k4m, but there was no significant sensitivity in the GRAIL dataset for degrees higher than l = 3.
Inversion procedure
To constrain the structure of the lunar interior based on GL1800F, we carry out a Bayesian inversion using MCMC with a Metropolis–Hastings sampling algorithm using PyMC. For our inversion, we vary elastic parameters relative to a reference lunar interior to fit observed k2m and k3m Love numbers (Table 1)72. Our detailed procedure is described below.
Our reference model incorporates both 1D structure and lateral variations in crustal thickness (and density) a priori. We extract 1D (that is, radial) elastic parameters and density for reference models from ref. 27 that constrains lunar structure using the satellite’s mean density and seismic wave arrival times (see Extended Data Table 1 for assumed mean shear modulus, bulk modulus and density values for each internal layer). Whereas moment of inertia can be used to further refine the interior structure of reference models, this constraint primarily informs the size of the lunar core (at more than 1,400 km depth) and therefore has minimal impact on interpretations of k2m or k3m in this study29,10,73,74 (Fig. 1b). Nominal viscosity for each layer is set to effectively infinite values (1030 Pa s). To account for variations in crustal structure25, we vary spherical harmonic coefficients describing shear modulus, bulk modulus and density for two adjacent internal layers (extending from 0 to 34 and 34 to 62 km in depth) following the method described in ref. 20 (see Extended Data Fig. 4a for assumed coefficient values).
We consider both 1D and 3D perturbations to the shear modulus and do not consider changes in density (that is, which may violate constraints from static gravity measurements, Fig. 3a or ref. 25) or bulk modulus (which have a negligible effect on \(k_2m\) or \(k_3m\), see ref. 20). As shear modulus (μ) is related to shear wave speed (Vs) and density (ρ) through \(\mu =\rho V_\rms^2\), our approach effectively perturbs Vs while maintaining fixed ρ within each model layer. We consider a total of 34 parameters: 30 parameters describing 3D variations of shear modulus \((\mu _lm^\prime )\) (that is, l = 1–3 spherical harmonic coefficients for the crust and mantle) and four parameters describing 1D structure \((\mu _00^\prime )\) (that is, l = 0 coefficients for the crust, the 34- to 734-km region, the 734- to 1,257-km region and the 1,257- to 1,407-km region). These model parameters are sampled as coefficients for spherical harmonic basis functions that comprise the base-10 logarithm (denoted by the symbol ′) of the ratio of the spatially variable shear modulus μ to that of the reference model μref for each internal layer:
$$\log _10\frac\mu \mu _\rmref=\mathop\sum \limits_l=0^3\mathop\sum \limits_m=-l^l\mu _lm^\prime Y_lm(\theta ,\lambda ),$$
(4)
where \(\mu _lm^\prime \) are sampled coefficients and \(Y_lm(\lambda ,\theta )\) are real form, ortho-normalized spherical harmonic basis functions (λ is the longitude, and θ is the colatitude in the COM reference frame):
$$Y_lm(\theta ,\lambda )=\left\{\beginarrayc\sqrt\frac12\rm\pi N_lm\barP_lm(\cos \theta )\cos (m\lambda ),\rmfor\,m > 0,\\ \sqrt\frac14\rm\pi N_lm\barP_lm(\cos \theta ),\rmfor\,m=0,\\ \sqrt\frac12\rm\pi N_ \barP_lm(\cos \theta )\sin (| m| \lambda ),\rmfor\,m < 0.\endarray\right.$$
(5)
We expand shear modulus structures for accepted candidate models into spherical harmonics (in postprocessing) to compute percentage perturbations μlm (that is, values presented in Fig. 2 and Extended Data Table 2):
$$\frac\mu \mu _\rmref=1+10^-2\mathop\sum \limits_l=0^3\mathop\sum \limits_m=-l^l\mu _lmY_lm.$$
(6)
The Maxwell viscosity η of the 1,257- to 1,407-km depth layer is computed by assuming l = 0 perturbations to the shear modulus of this layer correspond to changes in this layer’s effective shear modulus μeff (that is, the amplitude of the complex shear modulus at the monthly timescale):
$$\eta =\frac\mu _\rmref{\omega \sqrt\left(\frac\mu _\rmref\mu _\rmeff-1\right)}$$
(7)
where ω = 2.661 × 10−6 s−1 is the angular frequency corresponding to the lunar sidereal monthly period and
$$\mu _\rmeff=\mu _\rmref(1+10^-2\sqrt4\rm\pi \mu _00).$$
(8)
Coefficients for sampled l = 1 to l = 3 structure (that is, \(\mu _lm^\prime \) in equation (4)) are assumed to have uniform (that is, flat) prior probability distributions. Note that our method does not necessarily require the use of spherical harmonics as basis functions for calculations. For example, a 2–3% amplitude spherical cap (placed at the sub-Earth point) spanning the nearside hemisphere is sufficient to explain the observed 2–3% (l = 1, m = 1) variation in mantle shear modulus derived in this work. By contrast, we assume sampled \(\mu _00^\prime \) coefficients have Gaussian prior distributions with variances extracted from ref. 27. We separately sample \(\mu _00^\prime \) coefficients for regions between 34- to 734 km-, 734- to 1,257-km and 1257- to 1,407-km depths (that is, the lunar low-velocity zone or LVZ) to account for differences in mean shear modulus uncertainty for these regions (the variance for \(\mu _00^\prime \) in the LVZ is set to infinity)27. Increasing the variances of the \(\mu _00^\prime \) coefficients tends to distribute reductions in the mean shear modulus (required to explain high degree-2 Love numbers, Fig. 1a) to each layer, thereby increasing the inferred Maxwell viscosity of the LVZ from equation (7). Moreover, changing the assumed model for viscoelasticity (for example, from Maxwell to Kevin–Voigt) alters the inferred viscosity value(s) associated with a roughly 97% reduction in the effective shear modulus of the LVZ at the sidereal monthly period (relative to the effective shear modulus at seismic timescales, Extended Data Table 2) by up to an order of magnitude. Note that all sampled coefficients \(\mu _lm^\prime \) (that is, not just \(\mu _00^\prime \)) could, in principle, represent changes in effective shear modulus μeff and (by extension) variations in internal viscosity. However, only significant lateral changes in viscosity in the LVZ (that is, due to variations in temperature near the lunar mantle’s solidus in this region) are likely to drive substantial variation in μeff as per equation (7). This suggests that the inferred 2–3% variation in mantle shear modulus may reflect a pronounced lateral viscosity variation within the LVZ. However, without extra constraints, it remains unclear to what extent inferred asymmetries localize to any region of the deep interior or are indicative of a broader (for example, mantle wide) anomaly (main text discussion).
We generate an ensemble of internal structure models for Markov chains by sampling prior probability distributions for model parameters and forward computing Love numbers using these values. Each ensemble consists of roughly 1,000 individual accepted model realizations (that is, 50,000 samples total from 50 walkers). To speed up convergence, we consider only shear modulus perturbations and sample harmonic coefficients describing this structure up to l = 3 for inversions (earlier discussion). We also adopt an adaptive sampling approach (the ‘tune’ functionality in PyMC) that dynamically adjusts step sizes on the basis of the sensitivity of model outputs to input parameters72. We visually inspect Markov chains to discard initial burn-in steps (that is, typically the first roughly 10–20% of samples) and terminate inversions when parameter autocorrelations are greater than 0.99. Walker positions are updated on the basis of a likelihood function that considers only degree-2 and degree-3 Love number values (case 2 of Table 1):
$$\textlogL\propto -\frac12(\bfX-\bfY)^T\Sigma ^-1(\bfX-\bfY),$$
(9)
where X is the vector of observed Love numbers and Y is the vector of model-predicted Love numbers. Σ is a matrix that considers both observational and model covariances \((\Sigma =\Sigma _\rmobs+\Sigma _\rmmod)\). Both Σobs and Σmod are assumed to be diagonal (that is, each Love number observation and model parameter is independent). Note that differences between observations and modelled Love numbers (X − Y) yield maximum L values of roughly 0.8 (out of a possible 1) across our ensemble of accepted models, supporting our interpretation that k3m observations can be adequately explained by a nearside–farside asymmetry in the interior (Extended Data Fig. 2). Other system constraints (for example, mean density, moment of inertia or quality factors) are not incorporated into vectors X or Y in equation (9).
Modelling tidal deformation
We compute lunar Love numbers using the semi-analytic spectral method LOV3D (ref. 3), which solves mass conservation, momentum and Poisson’s equations in the Fourier domain for a laterally heterogeneous body subject to tidal loading:
$$\rho ^\prime =-\rho _(\nabla \cdot \bfu)-\bfu\cdot \nabla \rho _$$
(10)
$$\nabla \cdot \sigma ^\prime -\rho _\nabla (g\bfu\cdot \bfe_r)+g\rho _(\nabla \cdot \bfu)\bfe_r-\rho _\nabla \varphi ^\prime =0$$
(11)
$$\nabla ^2\varphi ^\prime =4\pi G\rho ^\prime $$
(12)
where u is the displacement vector, σ′ is the incremental material stress tensor, er is the radial unit vector, g the gravitational acceleration of the unperturbed body, \(\rho ^\prime \) is the incremental local density, G is the universal gravitational constant, ρ0 is the density of the unperturbed body and \(\varphi ^\prime \) is gravitational potential arising from tides and mass movement driven by deformation. We use the constitutive equation for isotropic linear elasticity to relate σ′ and u:
$$\sigma \prime =\left(\kappa -\frac23\mu \right)(\nabla \cdot \bfu)I+\mu (\nabla \bfu\cdot \nabla \bfu^T)$$
(13)
where I is the identity matrix and μ and κ are the shear and bulk moduli. We find minimal differences (less than 0.01%) between results produced by our methodology and numerical (that is, finite-element) solutions for displacement on a laterally heterogeneous moon subject to tidal loading. Moreover, our results for perturbations to the lunar gravity field for lunar interiors with l = 1, m = 1 shear modulus structure are broadly consistent with results presented in fig. 1 of ref. 4.
We discount the influence of polar motion—the movement of a planetary body’s rotational axis relative to its surface—on calculations of degree-2 and degree-3 Love numbers. This simplification is based on our expectation that the body tides considered in our work induce only minimal changes to the Moon’s moment of inertia tensor over the GRAIL observation period. To verify this assumption, we computed the amplitude of polar motion resulting from a static degree-2, order-1 bulge of 1 cm height. The resulting value, roughly 10−3 degrees, is orders of magnitude smaller than the Moon’s roughly 6.7° obliquity (that is, which is the dominant driver of degree-2, order-1 forcing for the Moon). Nonetheless, we expect that polar motion may substantially influence longer-term response to surface loading (for example, fig. 3a,b in ref. 75).
LOV3D explicitly computes coefficients \(K_l^\prime ,m^\prime ^l,m\), or ‘Extended Love numbers’ (distinct from the ‘traditional’ Love numbers klm described in equation (3)). \(K_l^\prime ,m^\prime ^l,m\) represents coupling between forcing at one harmonic (at l′, m′) and gravitational response to this forcing at another harmonic (at l, m) for a given interior structure. For a laterally heterogeneous body, equation (3) can be derived considering a general expression for perturbations to gravity field coefficients \(\Delta C_lm\) and \(\Delta S_lm\) in terms of real form \(K_l^\prime ,m^\prime ^l,m\):
$$\beginarrayc\Delta C_lm-\rmi\Delta S_lm=\mathop\sum \limits_l^\prime =2^3\mathop\sum \limits_m^\prime =0^l^\prime \frac12l^\prime +1\sum _j\frac\rmG\rmM_j\rmG\rmM\fracR^l^\prime +1r_j^l^\prime +1P_l^\prime m^\prime (\sin \phi _j)\\ \,\,\,\,\,\,\,[(K_l^\prime ,m^\prime ^l,m\cos (m^\prime \lambda _\rmj)+K_l^\prime ,-m^\prime ^l,m\sin (m^\prime \lambda _\rmj))\\ \,\,\,\,\,\,\,-\rmi(K_l^\prime ,m^\prime ^l,-m\cos (m^\prime \lambda _\rmj)+K_l^\prime ,-m^\prime ^l,-m\sin (m^\prime \lambda _\rmj))].\endarray$$
(14)
In this work, we make the following simplifications:
-
(1)
Gravity field inversions assume that perturbations \(\Delta C_30\), \(\Delta C_31\), \(\Delta C_32\), \(\Delta C_33\), \(\Delta S_31\), \(\Delta S_32\) and \(\Delta S_33\) are not affected by coupling that is temporally out of phase with forcing at these harmonics. We correspondingly set \(K_l^\prime ,m^\prime ^l,-m\), \(K_l^\prime ,-m^\prime ^l,m\) and \(K_\mathrm2,1^\mathrm3,1\), \(K_\mathrm2,1^\mathrm3,3\), \(K_\mathrm2,0^\mathrm3,0\), \(K_\mathrm2,0^\mathrm3,2\), \(K_\mathrm2,2^\mathrm3,0\), \(K_\mathrm2,2^\mathrm3,2\), \(K_2,-2^3,-2\), \(K_2,-1^3,-1\) and \(K_2,-1^3,-3\) to zero a priori.
-
(2)
To improve computational efficiency, we assume \(K_l^\prime ,m^\prime ^l,m=K_l^\prime ,-m^\prime ^l,-m\). However, we note that limited MCMC results (roughly 5,000 accepted candidate models) indicate that separate computations of Love numbers that assume \(K_l^\prime ,-m^\prime ^l,-m\ne K_l^\prime ,m^\prime ^l,m\) does not substantially (less than 1%) alter results presented in Figs. 2–4 and Extended Data Figs. 4b and 5.
On the basis of these assumptions, we can rewrite equation (14):
$$\Delta C_lm-\rmi\Delta S_lm=\mathop\sum \limits_l^\prime =2^3\mathop\sum \limits_m^\prime =0^l^\prime \fracK_l^\prime ,m^\prime ^l,m2l^\prime +1\sum _j\frac\rmGM_j\rmGM\fracR^l^\prime +1r_j^l^\prime +1P_l^\prime m^\prime (\sin \phi _j)\rme^-\rmim^\prime \lambda _j.$$
(15)
Note that we can compute individual components of the tidal forcing potential \(V_l^\prime m^\prime \) from equation (15):
$$V_l^\prime m^\prime =\frac12l^\prime +1\sum _j\frac\rmGM_j\rmGM\fracR^l^\prime +1r_j^l^\prime +1P_l^\prime m^\prime (\sin \phi _j)\rme^-\rmim^\prime \lambda _j.$$
(16)
Comparing equations (16), (15) and (3), it becomes apparent that traditional Love numbers klm represent the ratio of tidal (that is, forcing) potentials at (l′, m′) and response at (l, m) (that is, \(V_l^\prime m^\prime \) and \(V_lm\) from equation (15)) scaled by \(K_l^\prime ,m^\prime ^l,m\):
$$k_lm=\mathop\sum \limits_l^\prime =2^3\mathop\sum \limits_m^\prime =0^l^\prime K_l^\prime ,m^\prime ^l,m\fracV_lmV_l^\prime m^\prime .$$
(17)
In the case of a spherically symmetric Moon, Extended Love numbers simplify to klm when \(l=l^\prime \) and \(m=m^\prime \) (for example, \(K_30^30=K_31^31\,=\,\)\(K_32^32\,=\,K_33^33=k_3\) and \(K_20^20=K_21^21=K_22^22=k_2\)). However, for lunar interiors with degree-1 order-1 shear modulus variations, extra coupling terms (that is, \(K_20^31\), \(K_22^31\), \(K_22^33\), \(K_21^30\), \(K_21^32\)) become significant such that \(k_31\approx K_31^31+K_20^31V_20/V_31+K_22^31V_22/V_31\) and \(k_33\approx K_33^33+K_22^33V_22/V_33\) (equation (17))4. Note that ref. 4. approximate \(V_3m/V_2m=1/220\). Using our exact numerical approach to compute tidal potentials (equation (16)) we find \(V_3m/V_2m\) ranges from roughly 1/200–1/300.
Using our MCMC method, we also examine whether an unconstrained spherically symmetric lunar interior (that is, with all 1-σ bounds on mean shear modulus values for internal layers in Extended Data Table 1 set to infinity) could theoretically explain observed Love number values. We find that these inversions require a 70–100% reduction in mean μeff within the uppermost 100–200 km of the Moon relative to values presented in Extended Data Table 1 to explain k3m and k2m in Table 1 (the required perturbations are shallow because k3m are more sensitive to such perturbations than k2m). Such reductions suggest an unrealistically weak upper mantle or crust (for example, viscosities in equation (8) ranging from 109 to 1016 Pa s, which falls at least five orders of magnitude below expected values for this region).
Modelling temperature change
Our inference of a 100–200 K temperature difference (Fig. 3a) relies on linear relationships between temperature, shear modulus, density and composition (β, Δμ/ΔT, Δρ/ΔFo–Fa, Δμ/ΔFo–Fa) based on experimental studies of olivine. However, the lunar mantle probably contains at least roughly 5% pyroxene76, which may very slightly alter β, Δμ/ΔT, Δρ/ΔFo–Fa and Δμ/ΔFo–Fa (ref. 77). Phase changes could also cause deviations from this linear behaviour described by β, Δμ/ΔT, Δρ/ΔFo–Fa and Δμ/ΔFo–Fa; although such variations are probably confined to the LVZ. Minor phases (for example, ilmenite) may also be present in low concentrations throughout the lunar mantle78 but probably have a negligible effect on the results presented in Fig. 3a.