Subnanosecond flash memory enabled by 2D-enhanced hot-carrier injection

Device fabrication

The bottom control gates (5/15 nm Cr/Au) were patterned by e-beam lithography with a bilayer photoresist process followed by deposition of metal by e-beam evaporation on silicon dioxide (300 nm)/silicon substrates. For the flash memory, following the preparation of the bottom gates, an Al₂O₃ blocking oxide and an HfO₂ trap layer were grown by thermal atomic-layer deposition at 250 °C. During the atomic-layer-deposition process, trimethylaluminium and tetrakis(ethylmethylamino)hafnium reacted with water to form Al₂O₃ and HfO₂, respectively. This atomic-layer-deposition process is necessary only for flash fabrication. WSe₂, graphene and hBN bulk crystals were purchased from HQ Graphene and the heterostructure of the 2D materials was prepared using mechanical exfoliation and a dry-transfer approach. The hBN flake was first transferred to the bottom gate, and then the thin-body material was transferred onto the hBN flake. The adhesion of the heterostructure on the substrate was improved by heat annealing for more than 2 h at 200 °C under a nitrogen atmosphere. Next, drain–source contacts were patterned by e-beam lithography, and a metal stack (WSe₂, 10/12 nm Sb/Pt; graphene, 5/60 nm Cr/Au stack) was deposited using e-beam evaporation. After the standard lift-off approach, devices with the Sb/Pt contact were annealed by the hot plate in the glove box (200 °C, 2 h) to form the alloy. To conduct the sub-1-ns flash memory test, metal wires and pads matched with the radio-frequency probes were patterned by e-beam lithography, and 5/60 nm Cr/Au was deposited by e-beam evaporation.

Material characterization

Atomic force microscopy for the devices was measured by a MFP-3D Origin+ (Asylum Research, Oxford Instruments) system. The transmission-electron-microscopy-ready sample was prepared using an in situ focused ion-beam lift-out technique on a Thermo Scientific Helios Eurofins EAG lab G4 HX or UC Dual Beam focused ion-beam/scanning electron microscope. The sample was plated with iridium and capped with electron-beam Pt and ion-beam Pt before milling. The transmission electron microscopy image was captured with a Thermo Scientific Tecnai F20 transmission electron microscope operated at an accelerating voltage of 200 kV. Energy-dispersive spectroscopy was performed on the Super X FEI System under scanning transmission electron microscopy mode.

Electrical measurements

In this work, the devices were measured at room temperature and under atmospheric conditions in a probe station (MPI, TS200-SE). The 2D-HCI mechanism verification under various temperatures was performed using a Lake Shore vacuum low-temperature probe station under a vacuum of <10⁻⁴ mbar. The d.c. signals were generated using a source measure unit (B1500A, Keysight). The voltage pulses (≥20 ns) were generated using a semiconductor pulse generator unit (B1500A, Keysight). The sub-1-ns measurement was conducted based on our homemade high-speed system (Supplementary Fig. 19). The waveforms of the voltage pulse were captured by the oscilloscope (DPO 5204, Tektronix). The electrical test was conducted using a semiconductor device parameter analyser (B1500A, Keysight).

Theoretical derivation of quasi-2D model

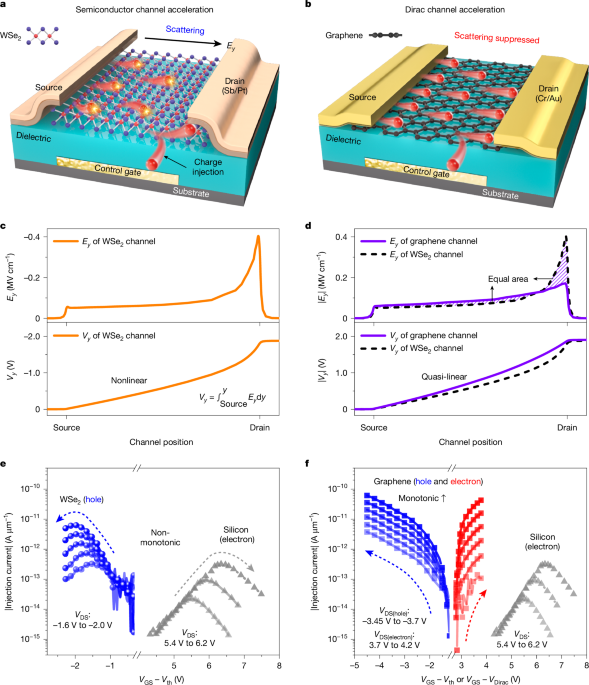
We employed a quasi-2D model with the same structure as our fabricated 2D transistor for analysis. The x direction is defined as the channel surface to gate vertically, and the y direction is defined as source to drain horizontally, where the zero point of the x and y axes is the channel surface and source, respectively. y₀ is at the leading edge of the velocity saturation region, V(y) is the horizontal potential in the channel, t_ch is the channel thickness, E_x and E_y are the vertical and horizontal electric field in the channel, E_dielectric is the vertical electric field in the dielectric, and E_sat and V_DSsat are the E_y and V(y) at the leading edge of the velocity saturation region, respectively. To obtain the E_y distribution, it is necessary to solve Poisson’s equation and the current transport equation simultaneously in the velocity saturation region. It is expressed as

where ρ(x, y) is the charge enclosed in the Gaussian box, ε₀ is the vacuum permittivity and ε_ch is the channel relative permittivity. Under the conditions of (1) the thin body (t_ch → 0) of the 2D material channel results in a square pinch-off region, denoted as a Gaussian box, (2) E_y only varies with horizontal position, and (3) the value of E_x at x = 0 is close to zero, which allows us to replace \(\frac\partial E_x\partial x\) with the average value given by \(\fracE_x(t_\rmch,y)t_\rmch\), we apply Gauss’ law

where E_dielectric is the electric field in the gate dielectric and ε_dielectric is the dielectric relative permittivity. Differentiating equation (5) with respect to y, we have

We can express E_dielectric(t_ch, y) as

where V_GS is the gate–source bias, V_FB is the flat-band voltage, φ_B is the surface potential and t_dielectric is the dielectric thickness. As the boundary conditions at the leading edge of the Gaussian box: V(y = y₀) = V_DSsat and E_dielectric(y = y₀) = [V_GS − V_FB − 2φ_B − V_DSsat]/t_dielectric, we can obtain that \(\rho (x,y)=\frac\varepsilon _\varepsilon _\rmdielectrict_\rmcht_\rmdielectric(V_\rmGS-V_\rmFB-2\varphi _\rmB-V_\rmDSsat)\). Then equation (6) is simplified to

where λ is the effective length of the Gaussian box, also known as the scale length. By applying the boundary conditions at the leading edge of the Gaussian box: V(y = y₀) = V_DSsat, and E_y(y = y₀) = E_sat, we can write the V(y) and E_y(y) in the Gaussian box as

and

At the drain end of the channel where the field peaks

and

where ΔL is the region that extends from the channel pinch-off point to the drain. Equations (11) and (12) can be combined to yield

and

This equation shows that the E_y,max is highly sensitive to t_ch scaling.