Strong-field quantum control in the extreme ultraviolet domain using pulse shaping

Strong-field phenomena play an important part in our understanding of the quantum world. Light–matter interactions beyond the perturbative limit can substantially distort the energy landscape of a quantum system, which forms the basis of many strong-field effects⁸ and provides opportunities for efficient quantum control schemes¹¹. Moreover, resonant strong coupling induces rapid Rabi cycling of the level populations¹², enabling complete population transfer to a target state². The development of intense extreme ultraviolet (XUV) and X-ray light sources has recently led to the investigation of related phenomena beyond valence electron dynamics, in highly excited, multi-electron and inner-shell electron states^{9,10,13,14,15,16,17}. Yet in most of these studies, the dressing of the quantum systems was induced by intense infrared fields overlapping with the XUV and X-ray pulses. In contrast, the alteration of energy levels directly by short-wavelength radiation is more difficult. So far, only a few studies have reported XUV-induced AC-Stark shifts of moderate magnitude (≲100 meV), difficult to resolve experimentally^9,18,19,20.

Another important step in exploring and mastering the quantum world is the active control of quantum dynamics with tailored light fields^21,22,23. At long wavelengths, sophisticated pulse-shaping techniques facilitate the precise quantum control and even the adaptive-feedback control of many light-induced processes, in both weak- and strong-field regimes^{24,25,26,27,28}. Several theoretical studies have pointed out the potential of pulse shaping in XUV and X-ray experiments^29,30,31. As an experimental step in this direction, phase-locked monochromatic and polychromatic pulse sequences have been generated^32,33,34,35. Using this tool, coherent control demonstrations in the perturbative limit^32,35,36 and the generation of intense attosecond pulses were achieved³⁷. Moreover, ultrafast polarization shaping at XUV wavelengths³⁸ and chirp control for the temporal compression of XUV pulses³⁹ were recently demonstrated. However, spectral phase shaping, which forms the core of pulse-shaping techniques, has not been demonstrated for the control of quantum phenomena at short wavelengths. Here we establish spectral phase shaping of intense XUV laser pulses and demonstrate high-fidelity quantum control of the Rabi and photoionization dynamics in helium.

In the experiment, He atoms are dressed and ionized by intense coherent XUV pulses (I > 10¹⁴ W cm^−2) delivered by the seeded FEL FERMI (Fig. 1a). The high radiation intensity causes a strong dressing of both the bound states in He and the photoelectron continuum, whereas the dynamics of the quantum system are still in the multiphoton regime (Keldysh parameter γ = 11). By contrast, the dynamics of a system dressed with near-infrared (NIR) radiation of comparable intensity would be dominated by tunnel and above barrier ionization (γ = 0.35) (ref. ⁸). Hence, the use of short-wavelength radiation provides access to a unique regime, in which the interplay between strongly dressed bound states and a strongly dressed continuum can be studied.

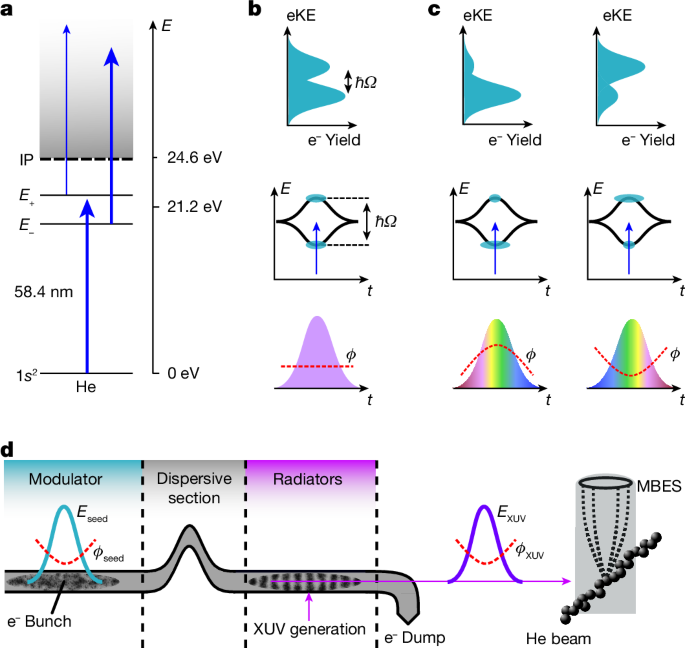
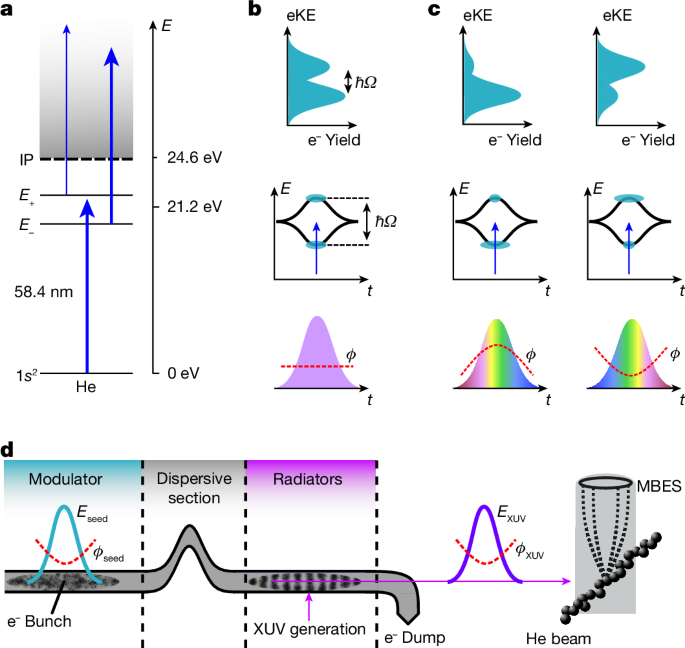
a, Intense XUV pulses dress the He 1s², 1s2p states and the electron continuum. E_± labels indicate the bound dressed states correlated to the 1s2p bare state. Mixing of p- and d-waves in the dressed continuum results in different coupling strengths to the dressed bound states (indicated by the thickness of the arrows). b,c, In the time domain, the AT splitting follows the intensity profile of the XUV field (middle). The dressed-state populations are monitored in the photoelectron eKE distributions (top). XUV pulse shaping enables the control of the non-perturbative quantum dynamics (bottom). For a flat phase ϕ (no chirp), both the excited dressed states are equally populated. For a positive phase curvature (up chirp), the population is predominantly transferred to the lower dressed state and the upper state is depleted, whereas for negative curvature (down chirp), the situation is reversed. d, Principle of XUV pulse shaping at the FEL FERMI. Intense seed laser pulses overlap spatially and temporally with the relativistic electron bunch in the modulator section of the FEL, leading to a modulation in the electron phase space. The induced energy modulations are converted into electron-density oscillations on passing a dispersive magnet section. The micro-bunched electrons then propagate through a section of radiator undulators, producing a coherent XUV pulse. In this process, the phase function of the seed pulse is coherently transferred to the XUV pulse, resulting in precise XUV phase shaping. The FEL pulses are focused on the interaction volume, exciting and ionizing He atoms. The photoelectrons are detected with a magnetic bottle electron spectrometer (MBES).

To dress the He atoms, we induce rapid Rabi cycling of the 1s²â€‰â†’ 1s2p atomic resonance with a near-resonant field E(t). The generalized Rabi frequency of this process is \(\varOmega ={\hbar }^{-1}\sqrt{{(\mu E)}^{2}+{\delta }^{2}}\), where μ denotes the transition dipole moment of the atomic resonance, δ the energy detuning and \(\hbar \) the reduced Planck constant. In the dressed-state formalism, the eigenenergies of the bound states depend on the field intensity and show the characteristic Autler–Townes (AT) energy splitting ΔE = ħΩ (ref. ⁴⁰). The observation of this phenomenon requires the mapping of the transiently dressed level structure of He while perturbed by the external field⁴¹. This is achieved by immediate photoionization over the course of the femtosecond pulses, thus projecting the time-integrated energy level shifts onto the electron kinetic energy (eKE) distribution (Fig. 1b).

Analogous to the bound-state description, the dressed continuum states are obtained by diagonalization of the corresponding Hamiltonian. The hybrid electron–photon eigenstates consist of a mixing of partial waves with different angular momenta, which alters the coupling strength to the dressed bound states of the He atoms (Fig. 1a).

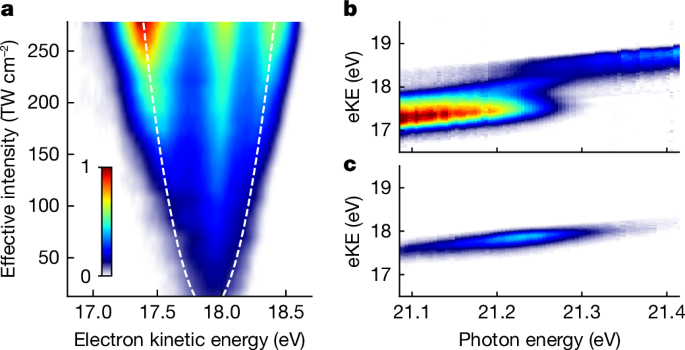
Figure 2 demonstrates experimentally the dressing of the He atoms. The build-up of the AT doublet is visible in the raw photoelectron spectra as the XUV intensity increases (Fig. 2a). The evolution of the AT doublet splitting is in good agreement with the expected square-root dependence on the XUV intensity \(\Delta E=\mu \sqrt{2{I}_{{\rm{eff}}}/({{\epsilon }}_{0}c)}\). Here, I_eff denotes an effective peak intensity, accounting for the spatially averaged intensity distribution in the interaction volume, ϵ₀ denotes the vacuum permittivity and c denotes the speed of light. The data can be thus used for gauging the XUV intensity in the interaction volume, a parameter otherwise difficult to determine. At the maximum XUV intensity, the photoelectron spectrum shows an energy splitting exceeding 1 eV, indicative of substantial AC-Stark shifts in the atomic level structure. The large AT splitting further implies that a Rabi flopping within 2 fs is achieved, offering a perspective for rapid population transfer outpacing possible competing intra- and inter-atomic decay mechanisms, which are ubiquitous in XUV and X-ray applications.

a, Detected photoelectron eKE distribution (raw data) as a function of the XUV intensity (FEL photon energy: 21.26 eV, GDD = 135 fs²). Dashed lines show the calculated AT splitting for an effective XUV peak intensity I_eff accounting for the spatial averaging in the interaction volume. b,c, Photoelectron spectra as a function of photon energy recorded for high XUV intensity (I_eff = 2.92(18) × 10¹⁴ W cm^−2) (b) and for lower intensity (I_eff ≈ 10¹³â€‰W cm^−2) (c). In b, an avoided crossing between the lower and higher AT band is visible directly in the raw photoelectron spectra. The photoelectron distribution peaking at eKE = 17.9 eV in a and b is ascribed to He atoms excited by lower XUV intensity (see text).

Figure 2b,c shows the photoelectron yield as a function of excitation photon energy. For high XUV intensity (Fig. 2b), the photoelectron spectra show an avoided level crossing of the dressed He states as they are mapped to the electron continuum (see also Fig. 4). Accordingly, at lower XUV intensity (Fig. 2c), the avoided crossing is not visible anymore. In the latter, the eKE distribution centres at 17.9 eV. In Fig. 2b, a similar contribution appears at the same kinetic energy that overlays the photoelectrons emitted from the strongly dressed atoms. Likewise, a notable portion of photoelectrons at eKE ≈ 17.9 eV in Fig. 2a does not show a discernible AT splitting. We conclude that a fraction of He atoms in the ionization volume are excited by much lower FEL intensity, which is consistent with the aberrated intensity profile of the FEL measured in the ionization volume (Extended Data Fig. 1). This overlapping lower intensity contribution does not influence the interpretation of the results in this work. For better visibility of the main features, we thus subtract this contribution from the data shown in Figs. 3 and 4.

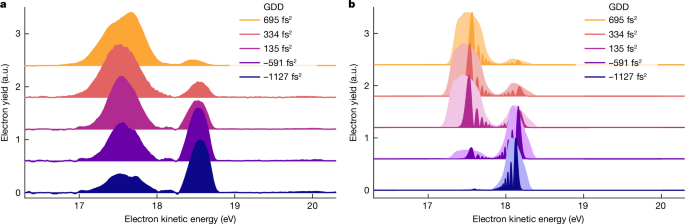
a, Photoelectron spectra obtained for phase-shaped XUV pulses (see labels for GDD values; photon energy = 21.25 eV; I_eff = 2.8(2) × 1,014 W cm^−2). The control of the dressed-state populations is directly reflected in the relative change of amplitude in the photoelectron bands. The small peak at 18.13 eV results from imperfect removal of the lower intensity contribution from the aberrated focus. b, Calculations of the time-dependent Schrödinger equation for a single active electron (TDSE-SAE) and a single laser intensity corresponding to the experimental I_eff = 2.8 × 10¹⁴ W cm^−2 (dark colours). Spectral fringes reflect here the temporal progression of the Rabi frequency during the light–matter interaction. The broadened photoelectron spectra (light colours) account for experimental broadening effects caused by the focal intensity averaging and the instrument response function. a.u., arbitrary units.

a, Photoelectron spectra as a function of energy detuning for different GDD values as labelled (I_eff = 2.92(18) × 10¹⁴ W cm^−2). b, TDSE-SAE calculations. Broadening by the instrument response function is omitted in the model. c, Amplitude ratio between the upper and lower photoelectron bands evaluated at the 1s²â€‰â†’ 1s2p resonance; hence, δ = 0. Experimental data (red), TDSE-SAE model treating the bound and continuum dynamics non-perturbatively (blue) and TDSE-SAE model applied to the bound-state dynamics, but treating the continuum perturbatively (yellow). d, Dependence of the He ionization rate on the spectral phase of the driving field. Data (red) and TDSE-SAE model (blue). a.u., arbitrary units.

The demonstrated dressing of He atoms provides the prerequisite for implementing the strong-field quantum control scheme (Fig. 1b,c). The main mechanism underlying the control scheme is described in the framework of the selective population of dressed states (SPODS), which is well established in the NIR spectral domain²⁸. Here, we extend SPODS to the XUV domain and include a new physical aspect—that is, the transition of the bound atomic system into a strongly dressed continuum. In SPODS, a flat phase leads to an equal population of both dressed states in the excited state manifold of helium; a positive phase curvature results in a predominant population of the lower dressed state and a negative phase curvature results in a predominant population of the upper dressed state (Fig. 1c). The scheme has been experimentally demonstrated with long-wavelength radiation⁴², in which pulse-shaping techniques are readily available. However, the opportunities for pulse-shaping technologies are largely unexplored for XUV and X-ray radiation.

We solve this problem by exploiting the potential of seeded FELs to allow for the accurate control of XUV pulse properties^39,43. These demonstrations have been so far limited to applications of temporal compression and amplification of the FEL pulses. By contrast, the deterministic control of quantum dynamics in a material system involves many more degrees of freedom, which makes the situation considerably more complex. The seeded FEL FERMI operation is based on the high-gain harmonic generation (HGHG) principle⁴⁴, in which the phase of an intense seed laser pulse is imprinted into a relativistic electron pulse to precondition the coherent XUV emission at harmonics of the seed laser (Fig. 1d). For FEL operation in the linear amplification regime, the phase ϕ_nH(t) of the FEL pulses emitted at the n’th harmonic of the seed laser follows the relationship³⁹

Here, ϕ_s denotes the phase of the seed laser pulses, which can be tuned with standard pulse-shaping technology at long wavelengths (Methods); ϕ_e accounts for the possible phase shifts caused by the energy dispersion of the electron beam through the dispersive magnet and is negligible for the parameters used in the experiment; and ϕ_a accounts for the FEL phase distortion due to the amplification and saturation in the radiator and has been kept negligibly small by properly tuning the FEL (Methods). Although complex phase shapes may be implemented with this scheme, for the current objective of controlling the strong-field induced dynamics in He atoms, shaping the quadratic phase term (group delay dispersion (GDD)) is sufficient⁴². Therefore, we focus on the GDD control in the following discussion.

Figure 3 demonstrates the quantum control of the dressed He populations. The eKE distribution shows a pronounced dependence on the GDD of the XUV pulses (Fig. 3a). At minimum chirp (GDD = 135 fs²), we observe an almost even amplitude in the AT doublet, whereas for GDD < 0, the higher energy photoelectron band dominates; for GDD  > 0, the situation is reversed. These changes directly reflect the control of the relative populations in the upper and lower dressed states of the He atoms. We obtain an excellent control contrast and the results are highly robust (Extended Data Fig. 2), which is remarkable given the complex experimental setup.

The experiment is in good agreement with the theoretical model (Fig. 3b) numerically solving the time-dependent Schrödinger equation for a single active electron (TDSE-SAE; Methods). To account for experimental broadening effects, we calculated the photoelectron spectra for a single intensity (corresponding to the experimental I_eff) and including the focal intensity average present in the experiment (Methods). All salient features of the experiment are well reproduced. The control of the dressed-state populations is in very good qualitative agreement. The different widths and shapes of the photoelectron peaks are qualitatively well-matched between the experiment and the calculations. The difference in the AT energy splitting between the experiment (ΔE_exp ≈ 1.02 eV) and theory (ΔE_theo = 0.74 eV) is in good agreement with the fact that the model underestimates the transition dipole moment of the 1s²â€‰â†’ 1s2p transition by a factor of 1.4 (Methods).

The high reproducibility, the excellent control contrast and the good agreement with theory confirm the feasibility of precise pulse shaping in the XUV domain and of quantum control applications, even of transient strong-field phenomena. This is an important achievement in view of quantum optimal control applications at short wavelengths.

The implemented control scheme is not restricted to adiabatic processes²⁸. In our experiment, the dynamics are adiabatic only for the largest frequency chirp (GDD = −1,127 fs²) (Extended Data Fig. 3). However, this also shows that the condition for rapid adiabatic passage² can be generally reached with our approach, offering a perspective on efficient population transfer in the XUV and potentially in the soft X-ray regime.

The active control of quantum dynamics with tailored light fields is an asset of pulse shaping. As another asset, systematic studies with shaped laser pulses can be used to uncover underlying physical mechanisms that are otherwise hidden. Here, we demonstrate this concept for pulse shaping in the XUV domain. The high XUV intensities used in our study lead to a peculiar scenario in which both bound and continuum states are dressed and a complex interplay between their dynamics arises. Hence, for a comprehensive understanding of the strong-field physics taking place, the bound-state dynamics and the non-perturbative photoionization have to be considered. This is in contrast to the strong-field control at long wavelengths, for which the continuum could be described perturbatively⁴².

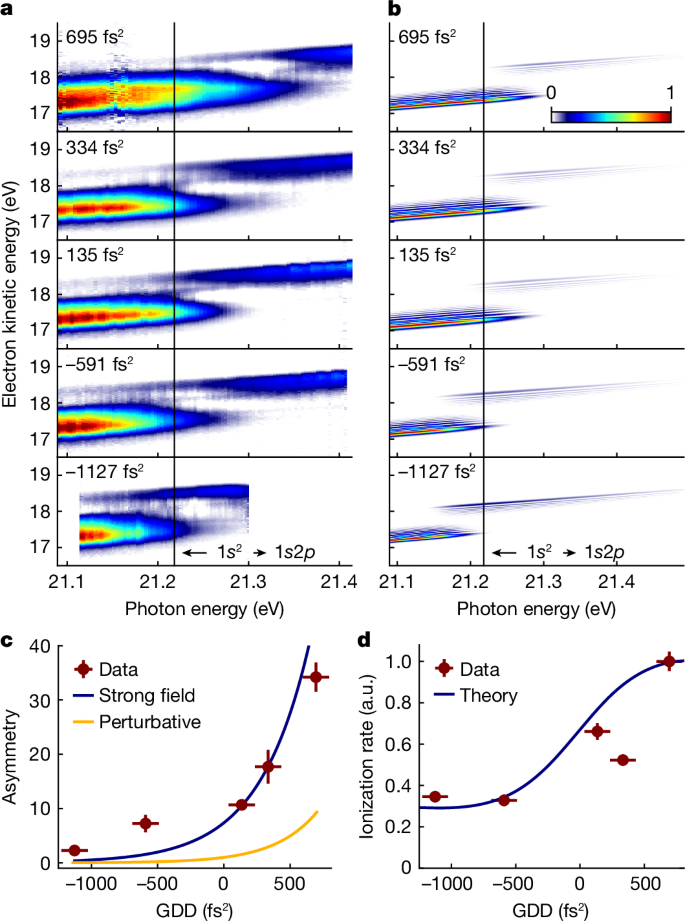
Figure 4a,b shows the avoided crossing of the photoelectron bands for different spectral phase curvatures applied to the XUV pulses. The experimental data show a clear dependence of the AT doublet amplitudes on the detuning and the GDD of the driving field, in good agreement with the theory. In the strong dressing regime, the bound–continuum coupling marks a third factor that influences the photoelectron spectrum. As predicted by theory, the strong-field-induced mixing of continuum states (Fig. 1a) leads to different photoionization probabilities for the upper and lower dressed states of the bound system⁴⁵. This is in agreement with the prevalent asymmetry of the AT doublet amplitudes observed in our data and calculations (Fig. 4a,b). An analogous effect is observed for the strong-field bound–continuum coupling in solid state systems⁴⁶.

To disentangle this strong-field effect from the influence of the detuning and spectral phase of the driving field, we evaluate the amplitude ratio between the upper and lower photoelectron bands at detuning δ = 0 eV (Fig. 4c). Interpolation to GDD = 0 fs² isolates the asymmetry solely caused by the strong-field bound–continuum coupling. We find reasonable agreement with our model when including the dressing of the ionization continuum (blue curve), in stark contrast to the same model but treating the continuum perturbatively (yellow curve). Hence, the dressing of the He atoms provides a probe of the strong-field dynamics in the continuum. This property is otherwise difficult to access and becomes available through our systematic study of the spectral phase dependence on the photoelectron spectrum.

Another possible mechanism for a general asymmetry in the AT doublet amplitudes could be the interference between ionization pathways through resonant and near-resonant bound states as recently suggested for the dressing of He atoms with XUV^20,47 and for alkali atoms with bichromatic NIR fields⁴⁸. In our experiment, we study the energetically well-isolated transition 1s²â€‰â†’ 1s2p, in which the contributions from neighbouring optically active states should be negligible. This provides us with a clean two-level system and greatly simplifies the data interpretation. For confirmation, we performed a calculation with a modified model in which any two-photon ionization through near-resonant states (except for the 1s2p state) was suppressed and, thus, possible photoionization interference effects were eliminated. Still, we observe a pronounced asymmetry in the AT doublet amplitudes (Extended Data Fig. 4). Moreover, owing to the large Keldysh parameter (γ = 11) and the low ponderomotive potential (U_p < 100 meV) in our study, other strong-field effects are expected to play a negligible part in the observed dynamics. We thus assign the experimental observation to the coupling of the dressed atom dynamics with a dressed ionization continuum induced by intense XUV driving fields.

A comprehensive understanding of the strong-field-induced dynamics in the system lays the basis for another quantum control effect, that is, the suppression of the ionization rate of the system, as proposed theoretically⁴⁵. The excitation probability for one-photon transitions is generally independent of the chirp direction of the driving field. However, if driving a quantum system in the strong-field limit, its quasi-resonant two-photon ionization rate may become sensitive to the chirp direction. We demonstrate the effect experimentally in Fig. 4d. A substantial reduction of the He ionization rate by 64% is achieved, solely by tuning the chirp of the FEL pulses while keeping the pulse area constant. The good agreement with the TDSE-SAE calculations confirms the mechanism. This control scheme exploits the interplay between the bound-state dynamics and the above-discussed selective coupling of the upper and lower dressed states to the ionization continuum. We note a stabilization mechanism of the dressed states in He was recently proposed, effectively causing also a suppression of the ionization rate⁴⁷. This mechanism requires, however, extreme pulse parameters, difficult to achieve experimentally. By contrast, our approach based on shaped pulses is more feasible and applies to a broader parameter range.

With this work, we have established a new tool for the manipulation and control of matter using XUV light sources. The demonstrated concept offers a wide pulse shaping window regarding pulse duration, photon energy and more complex phase shapes. In particular, the recent progress in echo-enabled harmonic generation^49,50 promises to extend the pulse-shaping concept to the soft X-ray domain (up to the 600 eV range) in which localized core electron states can be addressed. As such, we expect our work will stimulate other experimental and theoretical activities exploring the exciting possibilities offered by XUV and soft X-ray pulse shaping: first theory proposals in this direction have already been made^29,30,31. The demonstrated scheme already sets the basis for highly efficient adiabatic population transfer^1,2 and an extension to cubic or sinusoidal phase shaping would open up many more interesting control schemes^26,27. This may find applications, for example, in valence-core-stimulated Raman scattering or efficient and fast qubit manipulation with XUV and soft X-ray light. Furthermore, selective control schemes may reduce the influence of competing ionization processes ubiquitous in XUV and X-ray spectroscopy and imaging experiments, for which our work provides experimental demonstration. The generation of coherent attosecond pulse trains, with independent control of amplitude and phases, has been demonstrated at seeded FELs³⁷, bringing pulse shaping applications on the attosecond time scale within reach. This paves the way for the quantum control of molecular and solid state systems with chemical selectivity and on attosecond time scales.