Spatial metabolic gradients in the liver and small intestine

Animals

All mouse studies followed protocols approved by the Princeton Institutional Animal Care and Use Committee. Mice were housed under a normal light cycle (light, 08:00–20:00) and fed a standard rodent chow (PicoLab Rodent 20 5053) with access to water. The housing temperature was 20–22 °C and the relative humidity was 40–70%. Mice used were 12–18-week-old C57BL/6J male mice (The Jackson Laboratory). For spatial metabolomics experiments, mice were transferred to new cages with enrichment and water gel (ClearH2O, HydroGel) and without food at 08:30, fasted for 7 h and euthanized at 15:30 by cervical dislocation for tissue collection.

Jugular vein catheterization

Aseptic surgery was done to insert a catheter (Instech Labs) into the right jugular vein that was connected to a vascular access button (Instech Labs) implanted under the back skin of the mouse. Catheterized mice were individually housed in environmentally enriched (Bed-r’Nest, The Andersons) cages with ad libitum access to water and food. Mice were allowed to recover from jugular vein catheterization surgery for 5 days before experimentation. Catheters were flushed with heparin glycerol locking solution at least once every 5 days after surgery.

Glutamine infusion

[¹³C₅–¹⁵N₂]glutamine (99% ¹³C₅, 99% ¹⁵N₂, Cambridge Isotope Laboratories, CNLM-1275-H-0.5) solution was prepared in sterile saline at a concentration of 220 mM and filtered through a filter paper (pore size 0.45 µm). Jugular-vein-catheterized mice were transferred to individual cages without food at 08:00 on the day of infusion. At 12:00, the mice were weighed to calculate the tracer infusion rate. Catheters were then connected to infusion lines with a swivel and tether (Instech: swivel, SMCLA; line, KVABM1T/25) that allowed the animals to move freely in the cage. The tracer solution was infused (SyringePump, NE-1000) at the specified rate for 5 min to fill the catheter dead volume 1–2 h before starting the infusion, and mice were left to acclimatize. Infusions were started at 14:00 at a rate of 0.1 µl min⁻¹ per g body weight for 2.5 h and, at 16:30, the mice were euthanized by cervical dislocation for tissue collection.

Lactate infusion

[U-¹³C]l-lactate tracer (98% ¹³C, 20 w/w% solution, CLM-1579, Cambridge Isotope Laboratories) or [1-¹³C]l-lactate tracer (99% ¹³C, 20 w/w% solution, CLM-1577, Cambridge Isotope Laboratories) was diluted to 5% in sterile water. Mice catheterized in the right jugular vein and left carotid artery were fasted by switching to a fresh cage with no food at 08:00. At 12:00, the mice were weighed to calculate the tracer infusion rate, connected to the lines as described above and left in a cage for 1–2 h to acclimatize. At 14:30–15:30, infusion was initiated: a prime dose of 13 μl + 3 μl per gram mouse weight was provided over 22 s, and then the infusion rate was slowed to 0.3 μl min⁻¹ per gram mouse weight. After 2.5 h, mice were euthanized quickly by cervical dislocation, and tissues were collected for MALDI imaging.

Fructose and glucose oral gavage

A 1:1 mixture of [d₁₂]glucose (98%, DLM-9047-1, Cambridge Isotope Laboratories) and [U-¹³C]fructose (99%, CLM-1553-1, Cambridge Isotope Laboratories) in sterile saline was prepared. At 08:30, the mice were transferred to new cages without food. At 14:30, the mice were weighed to calculate the total volume to administer (10 μl per g body weight) and fed the tracer solution at a 1 g per kg dose through a plastic feeding tube (Instech Laboratories). Mice were euthanized by cervical dislocation either 90 s or 10 min after gavage and tissues were collected for MALDI imaging. The same process was done for mice that were administered glucose solution only (1 g per kg). For saline gavages (vehicle), 10 μl per g body weight of sterile saline was administered orally and mice were euthanized 10 min after gavage.

Liver and small intestine collection

For all liver imaging experiments, the left lateral liver lobe was collected within 1 min after euthanasia, placed onto a piece of aluminium foil, flash-frozen in liquid nitrogen and stored in a tightly sealed plastic bag at −80 °C until workup for imaging.

Intestine collection and preparation for IMS was optimized to preserve tissue integrity as follows: after mouse euthanasia, the small intestine was collected by cutting 1–2 cm below the pyloric sphincter and taking 5–10 cm of the small-intestine length. The proximal end of the intestine was handheld and the tip of an approximately 1-mm-gauge stainless steel needle connected to a syringe prefilled with optimal cutting temperature embedding medium (OCT) (at room temperature) was gently inserted about 0.5 cm into the lumen. The space between the lumen and the needle tip was partially sealed by gently pressing with the fingers. OCT was pushed into the lumen until it filled about 1 cm of the intestine and the OCT-filled fragment was cut and placed into a 22 × 30 mm × 20 mm (width × length × depth) polyethylene disposable histology mould (Peel-A-Way Tedpella) prefilled with an approximately 3-mm-high layer of OCT. Note that filling the intestine with OCT at high pressure (by pressing the syringe too hard) will result in tilted villi. Additional OCT was added to the mould to fully embed the intestines and placed onto dry ice until it was fully frozen. The entire process took around 5 min. Finally, the tissue mould was stored in a tightly sealed plastic bag at −80 °C until processed.

Tissue preparation for MALDI-IMS

Frozen tissues were transferred from −80 °C to a cryostat (Leica, CM3050S) at −20 °C and left to thermally equilibrate for around 30 min. For liver sectioning, frozen liver lobes were affixed by pouring a layer of OCT on cryostat stubs and placing the bottom of the lobe onto the OCT layer, and then left to freeze completely. For intestines, the OCT-embedded tissue block was removed from the mould and affixed to cryostat stubs as described for liver lobes.

Livers were sectioned in the transverse plane at a thickness of 10 µm and the sections were thaw-mounted onto pre-cooled (to cryostat temperature) indium tin oxide (ITO)-coated slides. Intestine blocks were sliced either longitudinally (that is, through the length of the intestine tubes) or across the intestine tubes (resulting in circular tissue section with the lumen at the centre and villi peripheral) at 10 µm thickness and thaw-mounted onto pre-cooled ITO slides. Tissue sections on ITO slides were kept frozen on dry ice in preparation for MALDI matrix coating. Serial sections were collected and thaw-mounted onto polylysine-coated glass slides and stored at −80 °C for immunofluorescence analysis.

MALDI matrix coating

Right before matrix coating, tissue slices on ITO slides were dried under a vacuum for 10–15 min. For liver MALDI imaging, we selected the MALDI matrix N-(1-naphthyl) ethylenediamine dihydrochloride (NEDC)⁵⁰ (222488, Sigma-Aldrich) and prepared a matrix solution at a concentration of 10 mg ml⁻¹ in 70%:30% (v:v) methanol:water. The dried tissue sections were coated with NEDC using an automated HTX sprayer (model HTX or model M3+) (HTX Technologies). NEDC was sprayed at a flow rate of 0.1 ml min⁻¹, nozzle velocity of 1,200 mm min⁻¹, nozzle temperature of 80 °C, nozzle height of 40 mm, drying gas pressure of 10 psi and a 30 s drying time between each pass, completing 10 passes over the entire slide.

For intestine MALDI imaging, we selected the matrix 1,5-DAN (56451, Millipore Sigma), which can produce homogeneous coating with small matrix crystal sizes⁵¹. The matrix solution was prepared at a concentration of 6 mg ml⁻¹ in 40%:40%:20% (v:v:v) methanol:acetonitrile:water. Dried tissue sections were coated with DAN using an automated HTX sprayer (model M3+; HTX Technologies) using the following spraying conditions: flow rate, 0.6 ml min⁻¹; nozzle velocity, 1,200 mm min⁻¹; nozzle temperature, 75 °C; nozzle height, 40 mm; drying gas pressure, 10 psi; and a 30 s drying time between each pass, for a total of 9 passes.

MALDI-IMS

All MALDI-IMS experiments were performed using the MALDI-2 timsTOF fleX (Bruker Daltonics) system equipped with microGRID technology (software, timsControl and FlexImaging). Mass calibration was performed using a Tuning Mix solution (Agilent Technologies, G1969-85000) before starting the imaging run. For liver and intestine imaging, acquisitions were recorded in negative-ion mode at a mass-to-charge ratio (m/z) range of 100–900. The energy difference between the collision cell and the quadrupole was set to 5 eV with a collision RF Vpp of 500 V. The quadrupole ion energy was set to 8 eV with a minimum m/z = 120, with a pre-TOF transfer time of 50 µs. Lock masses of m/z 124.0068 (taurine), m/z 255.2330 (palmitate), m/z 346.0558 (AMP), m/z 426.0222 (ADP) and m/z 514.2844 (taurocholic acid) were used for online calibration. Trapped ion mobility separation was not engaged during IMS runs.

For all MALDI imaging experiments, the laser Smart Beam was set to ‘custom’ mode while engaging ‘beam scan’. For liver imaging, a single burst of 150 laser shots was delivered to each pixel at a frequency of 5 kHz in a pixel area of 15 × 15 µm², and the raster step size was set to 15 µm in the x and y directions. For imaging livers from fructose-gavaged and lactate- and glutamine-infused mice, the spatial resolution was set to 20 µm and a total of 300 laser shots per pixel was used. For intestine imaging, a single burst of 75 shots was delivered at each pixel at a frequency of 5 kHz to a pixel area of 10 × 10 µm² and the raster step size was set to 10 µm. For 5-µm (intestines washed with acidic methanol) and 6-µm spatial resolution imaging of intestines, 25 laser shots were used and the step size was set to 5 µm or 6 µm, respectively. To ensure that matrix coating, laser energy, number of laser shots per pixel and beam focus on the sample surface were all optimized to yield the targeted spatial resolution, laser ablation marks after MALDI-IMS were inspected using bright-field microscopy under reflected-light illumination. Ablation marks were visibly isolated (that is, no oversampling) and the lateral distance between consecutive ablation marks was confirmed to be equal to the set step size in MALDI imaging.

Acidic methanol washing

In cases in which signal enhancement for phosphates (such as ATP) was necessary in the small intestine, tissue sections were washed with acidic methanol according to a previously developed protocol⁵². In brief, hydrophobic barriers on both sides of the tissue section were drawn with a hydrophobic pen (H-4000, Vector Laboratories) and the slide was placed on an incline with cotton balls (Thermo Fisher Scientific, 22-456-885) placed at the lower edge to adsorb the eluent. A total of 3 ml of ice-cold methanol with 0.05% (v:v) formic acid was pipetted onto the tissue sections and left to dry under vacuum before matrix coating.

H&E staining after MALDI-IMS

After MALDI-IMS analysis, the matrix was removed by placing the slide in ice-cold methanol for 5 min followed by 3 washes with 1× PBS for 5 min. The slides were briefly dipped in MilliQ water followed by immersion in haematoxylin for 10 min and then transferred to warm tap water for another 15 min. A second immersion in MilliQ water for 30 s was done and the slides were then dehydrated in a series of ethanol washes, beginning with 95% ethanol for 30 s, followed by eosin staining for 1 min to highlight cytoplasmic components. After eosin application, slides were returned to 95% ethanol for 2 min, followed by 2 min immersion in 100% ethanol and another 2 min in xylene. Finally, the slide was sealed with Cytoseal 60 and a cover slip was applied. Slides were imaged using a BioTek Cytation 5 Cell Imaging Multimode Reader (Agilent).

Immunofluorescence staining

Liver tissue slices were fixed with 4% paraformaldehyde (PFA), washed with PBS and incubated in PBS + 0.1% Triton X-100 for 1–2 h for permeabilization. Tissue slices were then blocked with 0.1% BSA in PBS + 0.1% Triton X-100 for 1 h and incubated with primary antibodies (EPCAM/TROP1 antibody, BLR077G, NBP3-14685, Novus Biologicals) at 1:200 dilution for 2 h at room temperature. The samples were then washed and incubated with fluorescent secondary antibodies (goat anti-rabbit cross-adsorbed secondary antibody, Alexa Fluor 568, A-11011, Invitrogen; 1:500) for 1 h, followed by mounting with Fluoromount-G (Southern Biotech, 0100-01) and imaging using the BioTek Cytation 5 Cell Imaging Multimode Reader (Agilent).

MALDI-IMS data processing

Raw IMS data were converted to .imZML format using SCiLS Lab (Bruker). The .imZML files were converted to .mat format using the custom developed MATLAB software (MATLAB 2024a) IsoScope (https://github.com/xxing9703/Isoscope). An initial set of around 800–1,000 m/z peaks was extracted from the raw data using the untargeted peak picking feature in IsoScope. In brief, this process filters peaks for which the mean signal across a subset of pixels is at least three times a predefined mean baseline. As this process does not filter out the background signal (including MALDI matrix peaks) and isotopologues, we matched m/z peaks with metabolites measured in-house by liquid chromatography–mass spectrometry (LC–MS) analysis of liver and intestine extracts within a mass window of ±15 ppm and with metabolites in the Human Metabolome Database (HMDB; https://hmdb.ca/) and lipids from LIPID MAPS (https://www.lipidmaps.org/), yielding 156 matching m/z peaks in the liver and 206 in the intestine. Of the 156 m/z peaks in the liver, 144 corresponded to deprotonated metabolites and lipids (the remaining 12 peaks comprised other ion adducts, such as [M+Na-2H]⁻, [M + K-2H]⁻ or [M+Cl]⁻; Supplementary Table 1). For the intestine, 176 ions corresponded to deprotonated metabolites and lipids, with the remaining 30 peaks as sodium, potassium, chloride adducts or dehydrated ([M-H₂O-H]⁻) (Supplementary Table 3). Ion intensities for the 156 metabolites and lipids in liver and the total ion count at each pixel were extracted and used for deep-learning analysis, whereas 206 metabolites and lipids were used for k-means clustering of the intestine data and subsequent analysis by MET-MAP. Note that, although glucose is one of several hexose isomers that cannot be distinguished in MALDI-TOF-IMS, glucose is the dominant isomer in the fasting liver based on LC–MS (Extended Data Fig. 4a) (ratio of glucose to other hexoses > 100) and, accordingly, we refer to hexose in fasting liver as glucose.

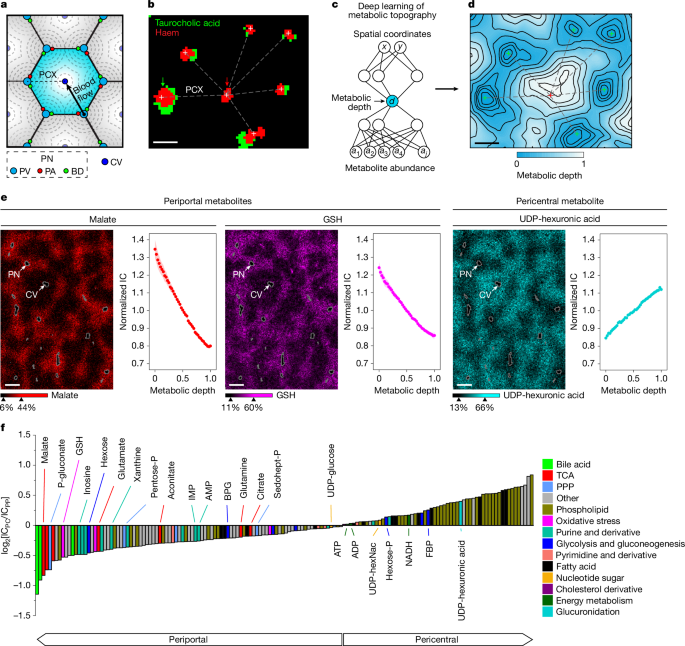
Deep learning of liver metabolic topography

We adapted GASTON⁵³, an unsupervised deep learning algorithm originally developed for spatial transcriptomics, to spatial metabolomics data. GASTON learns a topographic map of a 2D tissue slice in terms of a 1D coordinate called the isodepth, which is analogous to the height in a topographic map of a landscape. The key assumption of GASTON is that the expression of many genes is a function of the isodepth. Here we introduce the related algorithm MET-MAP, which learns a topographic map of a tissue slice from spatial metabolomics data by deriving a similar 1D coordinate, which we call the metabolic depth, under the assumption that the abundance of most metabolites is a function of the metabolic depth.

In brief, spatial metabolomics data consist of a metabolite abundance matrix \(A=[a_i,m]\in \mathbbR^N\times M\) where entry a_i,m is the abundance of metabolite m = 1, …, M in spatial location i = 1, …, N and a spatial location matrix \(S=[(x_i,\,y_i)]\in \mathbbR^N\times 2\) of which the rows contain the 2D coordinates (x_i,y_i) of location i = 1, …, N. We aim to learn a continuously differentiable function \(d:\mathbbR^2\to \mathbbR\), which we call the metabolic depth function, and a continuously differentiable function \(h_m:\mathbbR\to \mathbbR\) for metabolite m, which we call the 1D abundance function, such that the observed abundance a_i,m is approximately equal to the composition h_m(d(x_i,y_i)) of the metabolic depth function d and the 1D abundance function h_m; that is, a_i,m ≈ h_m(d(x_i,y_i)). We do this by parameterizing the metabolic depth d with a neural network and learning continuously differentiable functions h_m that minimize the mean squared error between the observed abundance a_i,m and the predicted abundance h_m(d(x_i,y_i)):

The value d(x_i,y_i) gives the metabolic depth at spatial location (x_i,y_i) and the gradient ∇d(x_i,y_i) indicates the spatial direction of maximum change in metabolite abundance. Details for the underlying model can be found elsewhere⁵³.

Before training the neural network to solve for metabolic depth d, raw metabolite abundance \([a_i,m]\in \mathbbR^N\times M\) was first normalized using total ion count (TIC) at individual pixels and log-transformed:

In liver samples, each tissue slice contained about 100,000 pixels. To ensure efficient training time and exclude low-quality regions such as tissue tears and distorted veins, we manually divided each tissue slice into non-overlapping rectangular crops of size 130 × 130 pixels. Each crop was then trained using the neural network to learn a metabolic depth for that specific crop. The metabolic depths of neighbouring crops were well matched at the boundaries.

MET-MAP allows for different number of hidden layers and nodes within each layer to parameterize the functions \(d:\mathbbR^2\to \mathbbR\) and \(h_m:\mathbbR\to \mathbbR\). For the liver, we trained the metabolic depth function using a single hidden layer with 400 nodes, and the 1D abundance functions using two hidden layers each with ten nodes (Supplementary Information). As the metabolic depth is scale invariant, we standardized the scales by performing a few transformations for easier interpretation and analysis. First, the metabolic depth results were scaled so that the contour lines of metabolic depth were equally spaced on the physical space with a range of 0 to 1. Then, to ensure that the metabolic depth followed the direction of the portal–central axis such that the minimum depth corresponded to the portal node, we scaled it using bile acid (taurocholic acid), which is known to enrich consistently in the periportal regions. Specifically, we transformed metabolic depth d to −d if corr(d, taurocholic acid) > 0.

Deep learning of intestinal epithelium metabolic topography

To isolate pixels that correspond to the epithelial layer in the intestine ion images, we performed k-means clustering (using the function in IsoScope) with input data of 206 metabolites and lipids. The number of clusters was set to provide clear isolation of pixels into epithelial layer, lamina propria, lumen and background (mostly ITO slide and matrix). The epithelial clusters were isolated and the ion intensities for those pixels were passed to MET-MAP for deep learning of spatial gradients.

In contrast to in the liver, initial manual inspection of raw metabolite abundance showed that metabolites in the intestine samples followed multiple distinct spatial patterns, two of the most dominant being the villus crypt-to-tip axis, and epithelial cell brush border-to-basal membrane axis (roughly bottom-to-top and outside-to-inside of villi, respectively). To model multiple distinct spatial patterns, we modified the neural network architecture of GASTON to learn K metabolic depths instead of a single depth. Given metabolite abundances \(A=[a_i,m]\in \mathbbR^N\times M\), spatial coordinates \(S=[(x_i,\,y_i)]\in \mathbbR^N\times 2\) and a parameter K, we learned a continuously differentiable function \(d:\mathbbR^2\to \mathbbR^K\), and M linear functions \(h_m:\mathbbR^K\to \mathbbR\). Each metabolite abundance is predicted as a weighted average of predictions from K metabolic depths \(d(x_i,y_i)\in \mathbbR^K\) learned, with the weights \(W\in \mathbbR^M\times K\) of the linear abundance mappings h_m, for m ∈ [M], where W_k,m represents the connection between the kth metabolic depths and mth metabolite abundance. Assuming individual metabolite abundances can in most cases be adequately described by one metabolic depth, we use Lasso regularization to encourage one metabolic depth weight to dominate while shrinking the other weights close to zero. The Lasso regularization encourages the K learned metabolic depths to be distinct and helps to reduce overfitting. Together, we learn

The K-dimensional latent variable \(d(x_i,y_i)\in \mathbbR^K\) models the K distant spatial-metabolic patterns desired. For the liver, we expected the portal–central gradient to be the predominant spatial axis. As such, we set K = 1. For the intestine, there are three relevant spatial dimensions: villus crypt-tip, epithelium apical-basolateral and intestine proximal-distal (the latter potentially also covering any macroscopic patterns arising from imperfect sample processing or analysis). As such, we set K = 3.

Similar to the data pre-processing in the liver, the intestine spatial metabolomics data were first normalized to the TIC and log-transformed. The number of epithelial pixels in each intestine sample was similar to the number of pixels in each crop of the previous liver samples, so we did not further crop the intestine samples.

We applied MET-MAP to the epithelial pixels to learn a metabolic depth function with two hidden layers of 120 nodes each, along with linear abundance functions (Supplementary Information). With visual assessment, one of the learned metabolic depths consistently captured the crypt-to-tip axis across all samples, validated by strong correlations with manually identified marker metabolites such as cholesterol sulfate and C20:3. In some samples, a second metabolic depth aligned with the brush border-to-basal membrane axis of epithelial cells, as indicated by strong correlations with metabolites such as linoleic acid. The third metabolic depth was typically associated with macroscopic spatial artifacts that varied between samples. The metabolic depth results were then scaled similarly as in liver results, where minimum metabolic depth corresponded to crypt regions in the crypt-to-tip axis.

Spatial gradient and statistics

After assigning metabolic depth values to pixels within a tissue crop, data were rebinned to 50 bins with an equal number of pixels. Raw metabolite ion counts were normalized to the median count across all pixels within a single tissue crop. Normalized ion counts that correspond to the same metabolic depth bin were then amalgamated from all crops across different mice. For the liver, we excluded pixels that colocalize with portal and central veins (1 ≤ metabolic depth ≤ 4 for portal nodes and 46 ≤ metabolic depth ≤ 50 for central veins) to measure spatial gradients between the two nodes. Using the amalgamated liver data at 5 ≤ metabolic depth ≤ 45, the normalized ion count as a function of metabolic depth was fitted to a linear model (in R v.3.6.6 and OriginPro 2024b). Using predicted ion counts from the model at metabolic depth = 5 (periportal, PP) and 45 (pericentral, PC), we computed the fold change, PC/PP, which defines the portal–central gradient in the liver. For the intestines, we used predicted ion counts from linear regression at metabolic depth = 49 (tip) and 5 (crypt), and the fold change tip/crypt defines the crypt-to-villus-tip gradient. P values from linear regression were adjusted for false positives using the Benjamini–Hochberg correction procedure. For flux spatial gradients, ratios or fractions were calculated at each pixel classified by the neural network and downstream analysis was applied as described above.

To compare gradients for UDP-glucose labelling in liver from ¹³C-fructose, ¹³Clactate or ²H-glucose, linear regression of labelling as a function of metabolic depth, tracer (dummy variable) and their interaction was performed (OriginPro 2024b) using labelling data for all pixels across all mice in the two compared groups (lactate versus fructose, lactate versus glucose or fructose versus glucose). P values for the interaction term were used to assess significant differences between labelling gradients for each tracer.

Spatial gradient plots

To plot the metabolite intensity signal as a function of metabolic depth, pixel data were binned to 50 metabolic depth bins as described above. Within each tissue crop, for each metabolite, the median raw ion count at each bin was normalized to the overall median ion count for that metabolite in the tissue crop. Means were then taken across all tissue crops from the same mouse. The mean and s.e.m. were then determined for each metabolite and bin across independent mice. Results were plotted for 5 ≤ metabolic depth ≤ 45 for liver and 5 ≤ metabolic depth ≤ 49 for intestine. Data were plotted in R v.3.6.6 (https://cran.r-project.org/) and OriginPro 2024b.

Spatial isotope tracing

Data collected from mice infused with isotopically labelled lactate or glutamine or administered labelled fructose were converted to .mat format as described above. Targeted metabolites of interest that were labelled by the tracer were added to the list of metabolites that were used in spatial metabolomics and passed to MET-MAP for analysis. After metabolic depth assignment, correction for natural abundance was first performed for each pixel using the software IsoScope. Fractional labelling at each pixel was calculated as follows:

where M_i is the fraction of a given isotopologue, n is the number of carbon or nitrogen atoms in the metabolite of interest and I_i is the raw ion count for a given isotopologue after natural isotope correction. Fractional labelling at each pixel was amalgamated across analysed samples and analysed by linear regression for spatial gradient measurement as described above.

Image processing

Raw ion images from livers and root-mean-square-normalized intestine images were exported from SCiLS Lab (Bruker) as OME-TIFF files without hotspot removal and processed with ImageJ. The colour scale was adjusted manually to optimize visualization. For liver, the haem image was binarized by thresholding and subtracted from other metabolite images. The binarized haem image was used to create vein outlines and overlaid with the desired metabolite image. Vein outlines were coloured grey and annotated as central or portal veins based on manual inspection of the taurocholic acid and PI(38:4) signals, the former localizing adjacent to portal veins and the latter to central. Images in Figs. 1–4 and Extended Data Figs. 1–9 were resized with Adobe Illustrator 2024.

Portal–central axis construction

To validate the results from MET-MAP, we established an orthogonal computational approach to infer portal–central gradients based on supervised machine learning. This orthogonal approach for automated portal–central axis construction involves three main steps: vein identification, vein classification and portal–central axis construction. Step 1 involves identifying central and portal veins, which is achieved by using ion images for haem, followed by 2D Gaussian filtering and binarization by thresholding. The positions of all vein centroids are registered. In step 2, we use an automated approach to classify the veins that were identified in step 1 as either central or portal. For each identified vein, a region of 12 × 12 pixels is cropped, with the vein being located at the centre of the region. Ion intensities for haem, taurocholic acid and arachidonic acid are extracted and the resulting three-channel image is classified as portal or central by a pretrained convolutional neural network model. This model uses high confidence, manually annotated veins as the training data and contains 6 layers: (a 3 × 3 × 3 convolution, a batchnorm, ReLU, 2 fully connected and a softmax layer). In step 3, all portal and central veins are connected by straight lines under bond length constraints (285 ≤ L ≤ 685 µm) to avoid joining central veins and portal nodes from distant lobules instead of the same one. To determine the position of a given pixel on a portal–central axis, the distance from the pixel to the PN is normalized to the total distance between the PN and CV, with 0 denoting the PN and 1 the CV. See the online Code Ocean capsule (https://codeocean.com/capsule/5032416/tree/v1) for supervised portal–central axis construction to facilitate analysis of the liver spatial metabolomics dataset.

Blood collection and serum preparation

Tail blood was sampled from live mice before euthanization, collected directly into Microvette-CB-300Z tubes (Sarstedt) and placed on ice. Tubes were centrifuged at 15,000g for 30 min at 4 °C, and serum was transferred to polypropylene tubes and stored at −80 °C.

Metabolites were extracted by adding 3–5 µl serum to 65 µl HPLC-grade methanol pre-cooled on wet ice, then vortexed and placed on dry ice for 15 min. The metabolite extract was then centrifuged at 15,000g for 15 min at 4 °C. The supernatant metabolite extract was diluted a further five to tenfold in HPLC-grade methanol, centrifuged again and the supernatant was transferred to LC–MS tubes for analysis.

LC–MS

Metabolites were measured using a quadrupole-orbitrap mass spectrometer (QExactive Plus, Exploris 240 or Exploris 480, Thermo Fisher Scientific) operating in negative-ion mode coupled to hydrophilic interaction liquid chromatography (HILIC) through electrospray ionization. Data were collected with Xcalibur v.4.3. Scans ranged from m/z 60 to 1,000 at 1 Hz and a resolution of ≥140,000. An XBridge BEH Amide column (2.1 mm × 150 mm, 2.5 µm particle size, 130 Å pore size; Waters) was used for LC separation with a gradient of solvent A (20 mM ammonium hydroxide in 95:5 water:acetonitrile, 20 mM ammonium acetate, pH 9.45) and solvent B (acetonitrile)⁵⁴. The flow rate was set 150 µl min⁻¹. The LC gradient was: 0 min, 90% B; 2 min, 90% B; 3 min, 75% B; 7 min, 75% B; 8 min, 70% B; 9 min, 70% B; 10 min, 50% B; 12 min, 50% B; 13 min, 25% B; 14 min, 25% B; 16 min, 0% B; 20.5 min, 0% B; 21 min, 90% B; 25 min, 90% B. The autosampler temperature was 5 °C, and the injection volume was set to 10 µl.

LC–MS data processing

LC–MS data were analysed using El-Maven (v.0.6.1). Ion counts were extracted and corrected for natural isotope abundance using the software isocorrCN (https://github.com/xxing9703/MIDview_isocorrCN). Serum enrichment was calculated as the ratio of the tracer abundance (that is, infused isotopic form) to the sum of ion counts for all isotopologues after natural isotope correction.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.