Soft magnetic hysteresis in a dysprosium amide–alkene complex up to 100 kelvin

General synthetic procedures

All manipulations were conducted under argon with the strict exclusion of oxygen and water using standard Schlenk and glove box techniques. Glassware was flame-dried under vacuum before use. Argon was passed through a column of activated 3-Å molecular sieves and copper catalyst before use. C₆D₆ was purchased anhydrous, degassed and stored under argon over activated 3-Å molecular sieves. C₆H₆ and n-hexane were refluxed over molten potassium for 3 days, distilled and stored under argon over a potassium mirror. C₆H₅F and hexamethyldisiloxane (HMDSO) were refluxed over CaH₂ for 3 days, distilled and stored under argon over activated 3-Å molecular sieves. LnI₃ (ref. ⁵³), [KN(SiⁱPr₃)₂] (ref. ²⁴) and [HNEt₃][AlOC(CF₃)₃₄] (ref. ¹²) were synthesized by literature methods, whereas 1-Y and 2-Y were prepared by procedures analogous to those for 1-Dy and 2-Dy, respectively.

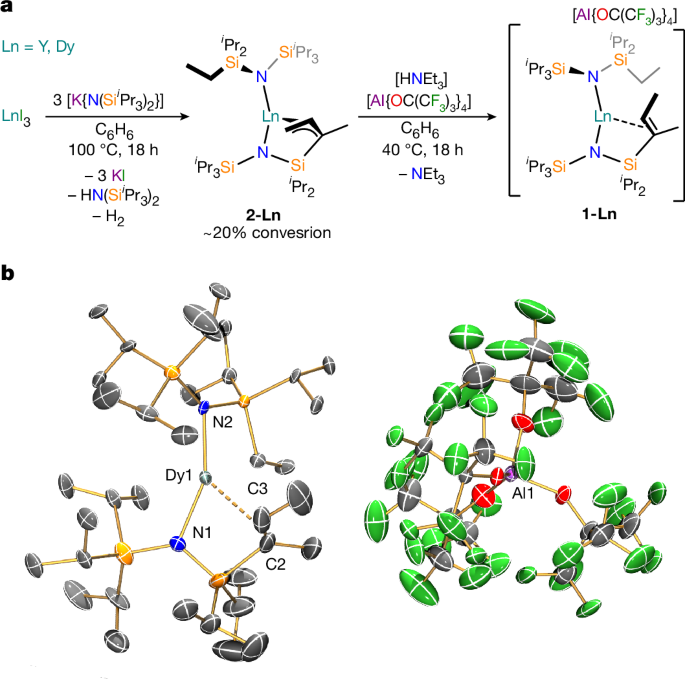
Synthesis of 1-Dy

A mixture of 2-Dy and HN{SⁱPr₃)₂, (1.620 g), prepared as described below from DyI₃ (2.720 g, 5.00 mmol) and [K{NSⁱPr₃)₂] (1.660 g, 4.50 mmol), was treated with [HNEt₃][AlOC(CF₃)₃₄] (1.07 g, 1.0 mmol) in C₆H₆ (20 ml) for 18 h at 40 °C. All volatiles were removed in vacuo, and the residues washed with n-hexane (about 3× 5 ml). The residues were dissolved in C₆H₅F (about 2 ml) and layered under n-hexane (about 20 ml), affording on diffusion a pale-yellow oil beneath colourless crystals of [HNEt₃][AlOC(CF₃)₃₄]. The oil was decanted into a clean flask and the crystallization process repeated nine times, at which point no additional [HNEt₃][AlOC(CF₃)₃₄] was observed in the residual oil by ¹H NMR spectroscopy. The final supernatant was decanted and 1-Dy was recrystallized by slow evaporation of residual solvent at ambient pressure. The crystalline material was triturated with excess n-hexane and dried in vacuo. Yield: 0.236 g, 0.132 mmol, 13% taking [HNEt₃][AlOC(CF₃)₃₄] as the limiting reagent. ¹H NMR (400.07 MHz, C₆H₅F): δ 3.26 (s), 2.69 (s), 2.59 (s), 2.33 (s), 1.95 (s), 1.67 (s), 1.21 (s). ¹⁹F NMR (376.40 MHz, C₆H₅F): δ −92.95 (s, CF₃). Anal. calcd. for C₅₂H₈₂AlDyF₃₆N₂O₄Si₄ (1,785.00 g mol⁻¹): C, 34.99; H, 4.63; N, 1.57. Found: C, 32.92; H, 4.20; N, 1.53. Fourier transform infrared spectroscopy (attenuated total reflectance (ATR), microcrystalline): \(\mathopv\limits^ \sim \) = 2,954 (m), 2,870 (m), 1,461 (m), 1,349 (m), 1,210 (s), 965 (s), 727 (s), 540 (s), 437 (s).

Synthesis of 2-Dy

A suspension of DyI₃ (1.630 g, 3.00 mmol) and [KN(SiⁱPr₃)₂] (3.303 g, 9.00 mmol) in C₆H₆ (20 ml) was stirred in a sealed ampoule at 100 °C for 18 h. The volatiles were then removed in vacuo, and the residues extracted into n-hexane (about 3× 10 ml). The volatiles were again removed to afford a viscous yellow oil containing a mix of 2-Dy and HN(SiⁱPr₃)₂; 2-Dy was subsequently isolated by crystallization from a concentrated HMDSO solution at −35 °C, followed by washing with cold HMDSO (<5 ml, –35 °C). Yield: 0.417 g, 0.510 mmol, 17%. ¹H NMR (400.07 MHz, C₆D₆): δ 1.79 (2), 0.98 (s). 0.70 (s), −0.45 (s), −2.38 (s), −9.14 (s). Anal. calcd. for C₃₆H₈₁DyN₂Si₄ (816.90 g mol⁻¹): C, 52.93; H, 9.99; N, 3.43. Found: C, 52.80; H, 10.34; N, 3.37. Fourier transform infrared spectroscopy (ATR, microcrystalline): \(\mathopv\limits^ \sim \) = 2,938 (s), 2,857 (s), 2,757 (w), 2,705 (w), 1,515 (w), 1,461 (s), 938 (s), 880 (s), 688 (s), 652 (s).

NMR spectra

NMR spectra were recorded at 298 K on a Bruker AVIII HD 400 cryoprobe spectrometer operating at 400.07 MHz (¹H), 100.61 MHz (¹³C), 376.40 MHz (¹⁹F) or 79.48 MHz (²⁹Si) MHz. Chemical shifts are reported in ppm and coupling constants in Hz. ¹H and ¹³C¹H DEPTQ NMR spectra, where DEPTQ is the distortionless enhancement by polarization transfer including the detection of quaternary nuclei pulse sequence, recorded in C₆D₆ are referenced to the solvent signal⁵⁴. NMR spectra recorded in C₆H₅F were locked to an internal sealed capillary of C₆D₆, with ¹H NMR spectra referenced using the highest intensity peak of the lower-frequency fluoroarene multiplet (δ_H 6.865) and ¹³C¹H DEPTQ spectra referenced to C₆D₆. ¹⁹F (C₇H₅F₃/CDCl₃) and ²⁹Si¹H DEPT90 (SiMe₄) spectra were referenced to external standards. Paramagnetic 1-Dy and 2-Dy did not exhibit resonances in their ¹³C¹H DEPTQ and ²⁹Si¹H DEPT90 NMR spectra, and we were not able to assign their ¹H NMR spectra; resonances between +400 ppm and −400 ppm are noted.

Infrared spectra

ATR infrared spectra of microcrystalline powders were recorded using a Bruker Alpha Fourier transform infrared spectrometer with a platinum-ATR module at ambient temperature. Elemental analysis (C, H, N) and inductively coupled plasma mass spectrometry samples were carried out by M. Jennings and A. Davies at the Microanalytical Service, Department of Chemistry, the University of Manchester. Elemental analysis values obtained for 1-Ln and 2-Ln typically gave carbon compositions that were lower than expected values. This phenomenon has commonly been ascribed to incomplete combustion owing to carbide formation in air- and moisture-sensitive complexes, as we have previously observed reproducibly for lanthanide N(SiⁱPr₃)₂ complexes^{21,24,55,56,57}. We also note that inconsistent results have been highlighted as an underlying issue with this analytical technique⁵⁸, with elemental analyses of fluorine-rich complexes such as 1-Ln highlighted as being particularly problematic⁵⁹.

Single-crystal X-ray diffraction

Single crystals of all compounds were mounted in Fomblin YR-1800 oil and XRD data were collected on a Rigaku FR-X diffractometer equipped with a HyPix-6000HE photon-counting pixel array detector and a mirror-monochromated X-ray source using Cu Kα radiation (wavelength λ = 1.5418 Å). Intensities were integrated from data recorded on 0.5° frames by ω-axis rotation, which is the axis perpendicular to the incident X-ray beam. Cell parameters were refined from the observed positions of all strong reflections in each data set. A Gaussian grid face-indexed with a beam profile was applied for all structures⁶⁰. The structures were solved using SHELXT⁶¹; the datasets were refined by full-matrix least-squares on all unique F² values, where F is the crystallographic structure factor⁶¹. Anisotropic displacement parameters were used for all non-hydrogen atoms with constrained riding hydrogen geometries, with the exception of borohydride hydrogen atoms, which were located in the difference map and refined isotropically; the hydrogen atom isotropic displacement parameter (U_iso) was set at 1.2 (1.5 for methyl groups) times the equivalent isotropic displacement parameter (U_eq) of the parent atom. The largest features in final difference syntheses were close to heavy atoms and were of no chemical relevance. CrysAlisPro⁶⁰ was used for control and integration, and SHELX^61,62 was employed through OLEX2⁶³ for structure solution and refinement. ORTEP-3⁶⁴ and POV-Ray⁶⁵ were used for molecular graphics. Plots of electron density maps were generated on Mercury 4.0⁶⁶.

Powder X-ray diffraction

Microcrystalline samples of 1-Dy, 1-Y, and 5%Dy@1-Y were mounted in Fomblin YR-1800 oil and powder XRD data were collected at 100 K between an incident angle (θ) of 3° and 70°, with a detector distance of 150 mm and a beam divergence of 1.0 mRad (ref. ⁶⁷), using a Rigaku FR-X rotating anode single-crystal X-ray diffractometer with Cu Kα radiation (λ = 1.5418 Å) with a Hypix-6000HE detector and an Oxford Cryosystems nitrogen flow gas system. The instrument was calibrated using the collected data, with the instrument model refined using diffraction peak positions measured at multiple detector angles. The data were collected, reduced and integrated using CrysAlisPro software⁶⁰. Peak hunting and unit cell indexing was performed using TOPAS software²⁷. Le Bail profile analysis was performed using JANA2006 software⁶⁷. The two broad peaks centred around approximately 16° and 42° 2θ are owing to scatter from the Fomblin YR-1800 oil.

Magnetic measurements

Magnetic measurements were performed using a Quantum Design MPMS3 SQUID magnetometer. Samples of 1-Dy (20.7 mg) and 5%Dy@1-Y (30.8 mg) were crushed with a mortar and pestle under an inert atmosphere, then loaded into a borosilicate glass NMR tube with eicosane flakes (1-Dy 21.3 mg; 5%Dy@1-Y 27.0 mg). Samples were gently heated to melt the eicosane and then cooled. The tube was flame-sealed (about 3 cm) under dynamic vacuum and mounted in a straw using Kapton tape. Data were corrected for the diamagnetism of the straw, NMR tube and eicosane using calibrated blanks, for the shape of the sample using Quantum Design Geometry Simulator (factors 0.996–1.034), and for the diamagnetism of the sample (estimated as the molecular weight (g mol^–1) multiplied by −0.5 × 10^–6 cm³ K mol^–1). The data for 5%Dy@1-Y were processed assuming 3.46% Dy, calibrated using the magnetization saturation value of 5.20 N_A µ_B for 1-Dy at 2 K, 7 T (Extended Data Fig. 5a). To calibrate the magnetic field, measurements were performed on a palladium standard at 298 K under identical field-charging conditions, outlying data points were removed, and the field correction versus the reported field was fitted to a sum of B-splines⁶⁸ (24, 21, 41 and 49 knots for 0–7 T, ±3 T, ±5 T and ±7 T) in Mathematica 12.3⁶⁹.

Direct-current susceptibility measurements were performed on 1-Dy with a 0.1-T field between 300 K and 2 K with a constant sweep rate of 0.5 K min^–1. For zero-field cooled, virgin magnetization, a.c. and waveform measurements, a magnetic reset was performed before cooling the sample. Susceptibility and hysteresis measurements were performed in vibrating sample magnetometer (VSM) mode with a 5 mm vibration amplitude and 2 s averaging time, except for the 2 K and 5 K hysteresis and virgin magnetization for which a 0.5 mm amplitude was used to minimize vibrational heating. The latter data were noisy: outliers (with large errors) were removed and data with |H| > 0.2 T were smoothed using parabolic-weighted adjacent averaging. Hysteresis measurements were performed with a constant a sweep rate of 22 Oe s^–1 between ±7 T at 2–50 K, and ±3 T at 60–120 K for 1-Dy and between ±7 T at 2 K, ±5 T at 10–20 K and ±3 T at 30–50 K for 5%Dy@1-Y. The coercive field and remanent magnetization were determined by interpolating the x and y intercept, respectively; values are reported as the average from positive and negative sweeps, with the uncertainty defined as half the difference.

Alternating-current susceptibility measurements were performed at 55–151 K (1-Dy) or 55–131 K (5%Dy@1-Y). Measurements were performed using 8 frequencies per decade between 0.1 Hz and 1,000 Hz (55–124 K) or between 1 Hz and 1000 Hz (127–151 K) for 1-Dy and 4 frequencies per decade between 0.1 Hz and 647 Hz (55–127 K) or between 1 Hz and 647 Hz (131 K) for 5%Dy@1-Y. An oscillating field of 5 Oe was used for 0.1–563 Hz, and a 2 Oe oscillating field for 750 Hz and 1,000 Hz. Averages for 1-Dy were performed for 4 s or 20 cycles (0.1–10 Hz), and 2 s or 10 cycles (13–1,000 Hz), whichever was longer. For 5%Dy@1-Y and T ≥ 91 K, averages were performed for 10 s or 50 cycles (0.1–10 Hz), 4 s or 20 cycles (13–87 Hz), or 2 s or 10 cycles (114–647 Hz). For 5%Dy@1-Y and T ≤ 87 K, averages were performed for 20 s or for 100 cycles (0.1–87 Hz) or 10 s or for 50 cycles (114–647 Hz). Waveform measurements were performed below 24 K with a field of ±8 Oe, a field sweep rate of 700 Oe s^–1, a fixed moment range of unity, and VSM mode with an amplitude of 1 mm (0.5 mm for 2 K) and a 0.5 s averaging time⁴³. Waveform frequencies in mHz (number of square-wave periods) for 1-Dy (* indicates frequencies used for 5%Dy@1-Y): 0.1 (2)*, 0.32 (2), 0.56 (2)*, 1.0 (2), 1.8 (2)*, 3.1 (2), 5.5 (3)*, 9.9 (4), 13 (5), 17 (6), 21 (6)*, 28 (7), 36 (8)*, 46 (9), 57 (10)*. In- and out-of-phase susceptibilities were extracted in CC-FIT2^70,71, disabling filtering based on error values and using a field window of ±0.3 Oe to discard data points from before and after the measurement. Alternating-current and waveform data were fit to the generalized Debye model, and the temperature dependence of magnetic reversal rates was fitted in CC-FIT2^70,71.

Electronic structure

CASSCF-SO calculations on 1-Dy and 2-Dy were performed with OpenMolcas 23.02⁷². The XRD geometry was used for each disorder component, excluding the anion for 1-Dy, as well as using the optimized geometry of the cation of 1-Dy from periodic DFT. We used the second-order Douglas–Kroll–Hess relativistic Hamiltonian⁷³, ANO-RCC basis sets⁷⁴ (VTZP for Dy, VDZP for N and coordinated allyl/alkene C, VDZ all other atoms), and the resolution of the identity approximation of two electron integrals with the Cholesky ‘atomic compact’ auxiliary basis set⁷⁵. State-averaged CASSCF calculations were performed with a 9 electrons in 7 4f orbital active space, considering 21 roots for total spin S = 5/2, 224 roots for S = 3/2 and 490 roots for S = 1/2. The CASSCF states were mixed with spin–orbit coupling including 21 S = 5/2 states, 128 S = 3/2 states and 130 S = 1/2 states. We projected the ⁶H_15/2 multiplet from the spin-orbit states to obtain the composition of the low-lying states in the m_J basis using molcas_suite⁷⁶.

Spin dynamics calculations

Following our established methodology^48,49,77,78, the solid-state structure of 1-Dy was optimized with DFT using the program VASP 6.1.2^79,80,81,82 with the PBE (Perdew–Burke–Ernzerhof) functional⁸³. We note that the choice of functional has a direct bearing on the calculated phonon DOS, which in turn directly impacts magnetization reversal rates; there is yet to be a systematic study of the impact of such considerations for SMMs, and we are currently working on this as a standalone study. We used a plane-wave-basis set up to 900 eV (determined via convergence testing) and sampled the electronic structure at the Γ point. Atomic positions and cell shape were optimized to a force tolerance of 0.001 eV Å⁻¹ starting from the XRD data of the major component. Phonons were calculated with phonopy⁸⁴.

To obtain the spin-phonon coupling, CASSCF-SO calculations were performed where the crystalline environment around a single 1-Dy cation was represented by a spherical cluster of unit cells (40 Å radius) composed of point charges (obtained from gas-phase DFT calculations on the cationic and anionic components of 1-Dy using CHELPG⁸⁵), and then surrounded further by a spherical conductor (Kirkwood solvent model with dielectric constant ε → ∞), which screens the unphysical surface charges to reproduce the Madelung potential⁴⁸. We used a 9-in-7 active space for 18 S = 5/2 states only, and other details as described above. The spin–phonon coupling for each phonon (index j) at each q-point \(\partial \widehatH/\partial Z_\bfqj\) was evaluated using our linear vibronic coupling method without recourse to a model Hamiltonian^77,78.

Magnetization reversal rates were calculated with Tau⁸⁶, considering one-phonon (Orbach and direct) and two-phonon (Raman-I) rates using perturbation theory expressions (equations 40, 41 and 46–49 in ref. ⁴⁹) with a magnetic field of 2 Oe along the main anisotropy axis. Integration was performed over anti-Lorentzian phonon lineshapes (equation 11 in ref. ⁴⁹, using full-width at half-maximum linewidths Γ = 0.1–100 cm⁻¹) within an equivalent range of μ ± 2σ (95%) using the trapezoidal method with 40 equidistant steps, and restricted to ω < 496.7 cm⁻¹ for the two-phonon terms. Very little dependence on linewidth is observed (Supplementary Fig. 46), much less than the distributions of experimental rates; Γ = 10 cm⁻¹ was chosen as the best compromise. Q-point meshes from 1 × 1 × 1 to 3 × 3 × 3 gave indistinguishable rates; meshes other than 1 × 1 × 1 included several imaginary phonons modes: removing them or setting the frequency to its absolute value result in near-identical rates. The spectral density was calculated as the product of the phonon DOS and the spin-phonon coupling strength per mode⁸⁷.

Hysteresis modelling

One- and two-phonon rates were calculated with Tau⁸⁶ as a function of field magnitude (at 2 Oe, and every 0.1 T from 0.1 T to 7 T), orientation (50 points with a hemispherical Fibonacci lattice⁸⁸), and temperature (every 2 K from 2 K to 120 K). (Note 1: our approach differs from Soncini and co-workers as we calculate phonons, spin–phonon coupling, and spin dynamics ab initio, whereas they used a model for spin–phonon coupling and assumed a Debye-like phonon spectrum^89,90. Note 2: the one-phonon rates show that, at low temperature, the direct mechanism within the ground doublet is quickly turned on in small fields and has a power-law field dependence at higher fields⁹¹, whereas the Orbach mechanism dominates with minimal field dependence at higher temperatures; the two-phonon Raman-I rates have a weak field dependence⁹², but it is non-zero owing to the splitting of the ground doublet interacting with a changing cross-section of phonons that can mediate the scattering process.) Similar calculations were performed for [Dy(Cp^ttt)₂][B(C₆F₅)₄] using phonons from ref. ⁵⁰, and restricting ħω < 99 cm⁻¹ for two-phonon rates. QTM rates are not included in our modelling, noting that the closing of the hysteresis at high temperature is dominated by phonon-driven processes where QTM is not relevant.

To calculate the hysteresis curve, we linearly interpolate state energies (E_i) and magnetic moments (M_i) as a function of field, and interpolate log₁₀(τ⁻¹) with two-dimensional cubic splines as a function of field and temperature. Then, we use symmetry relations to obtain values for negative fields (states n and \(\barn\) are Kramers pairs):

Initial-state populations (at −7 T or −3 T) were set to Boltzmann equilibrium. The magnetic field was swept at a rate of s = 22 Oe s^–1 towards either +7 T or +3 T, and state populations were propagated in time with a time step of Δt = 1 ms (required to converge calculated coercive fields to within 1 Oe; Supplementary Fig. 49). At time step t, the population vector P_t is:

where \(P_t^\rmeq\) is the equilibrium population at t, P_t−1 is the population at the previous time step, and \(\tau _t^-1\) is the calculated magnetization reversal rate at the given field strength, orientation and temperature. Only populations of the lowest four states were considered owing to the large energy gaps to excited states. At time step t, the net magnetization M_t is:

where M_n,t is the magnetic moment of state n and P_n,t is its population. M_t is converted into M(H) with H_t = H₀ − t × Δt × s, and the reverse sweep obtained by inverting the forwards sweep around both field and magnetization axes. This was performed for each field orientation and the resulting loops were integrated over the hemispherical grid to give the powder data. The coercive field was obtained by interpolation of powder data for each isotherm as a function of magnetic field.

Gas-phase DFT

A gas-phase DFT geometry optimization was performed on 1-Y. Calculations were performed with the hybrid PBE0 functional⁹³, with the def2-TZVP basis on all atoms⁹⁴, and the D4 dispersion correction⁹⁵, in ORCA 5.0.2⁹⁶. The geometry optimization was started from the crystal structure geometry. Quantum theory of atoms in molecules analysis was performed with Critic2^97,98.