Self-organized patterning of crocodile head scales by compressive folding

Animal husbandry

Fertilized crocodile eggs (imported from Seronera Crocodile Farm) were transported to the University of Geneva and incubated at 31 °C in moist vermiculite. All treated and non-treated crocodile embryos were fixed and stored in 10% neutral buffered formalin (NBF). All non-fluorescence imaging of embryonic crocodile samples was undertaken using the Keyence VHX 7000 digital microscope. Imaging of hatched crocodile specimens was undertaken using an overhead-mounted Nikon D800 camera. Maintenance of, and experiments with, crocodile embryos and juveniles were approved by the Geneva Canton ethical regulation authority (authorization GE10619B) and performed according to Swiss law. The sample sizes are specified in figure legends and the Supplementary Information. Randomization and blinding was not required.

Nanoindentation

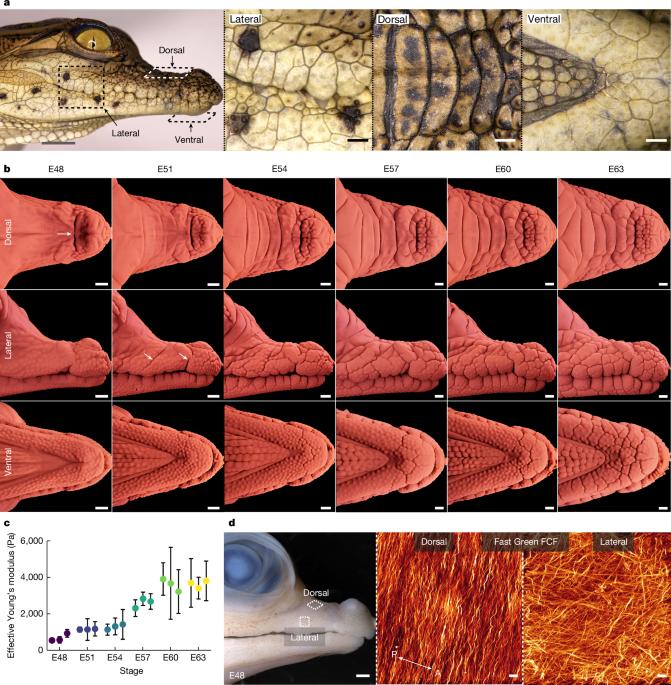
A Piuma nanoindenter (Optics11) was used to acquire stiffness measurements (effective Young’s modulus, Pa) of embryonic crocodile skin surface. When comparing measurements in two skin samples, a change in epidermal keratinization will produce a change in surface stiffness, which is very likely to be correlated with a change of the same sign in the effective overall Young’s modulus of the whole multilayered epidermis. In other words, an increase in epidermal surface stiffness is very likely accompanied by an increased stiffness of the whole epidermis. Freshly dissected upper jaws were positioned lateral side upwards, submerged in PBS. A probe with a tip radius of 99 µm and stiffness rating of 0.48 N m^−1 was used to indent at a depth of 2,000 nm. Only measurements from load-displacement curves with a Hertzian contact model fit of ≥95% were subsequently analysed. Each biological replicate for the embryonic nanoindentation series was indented 10 times (Fig. 1c) or 5 times (Fig. 2f). These indentation points were positioned in a single row with each point separated by 120 µm. Plots showing the mean effective Young’s modulus values for each biological replicate with s.d. are presented. Statistical analysis was undertaken in Prism 9 (GraphPad).

Confocal microscopy

Confocal microscopy was used for embryonic crocodile samples stained with the Fast Green FCF dye (Sigma-Aldrich) according to a protocol of whole-mount collagen staining²⁵. Image acquisition was undertaken as previously described²⁵, using the SP8 microscope (Leica Microsystems), with a ×63 oil-immersion objective (numerical aperture, 1.4). Fast Green was excited at 627 nm and the signal was detected in the range of 630–730 nm. Image reconstruction was undertaken using Imaris (Oxford Instruments).

H&E staining

Fixed embryonic crocodile samples were dissected and embedded in paraffin as previously described²⁴. Paraffin sections were cut at 10 µm with a RM2255 microtome (Leica Microsystems) before staining with haematoxylin and eosin (H&E). Slides were imaged using an automated slide scanner (3DHISTECH).

In ovo intravenous EGF injections in crocodiles

The injection of crocodile eggs was undertaken in accordance with our previously published work^20,21 (https://youtu.be/qCYWSgbffnY). Crocodile eggs were incubated until the appropriate developmental stage and then cleaned with 70% ethanol. Eggs were candled to identify a suitable vein for injection, and a detailing saw (Micromot 50/E, Proxxon) was used to remove the shell while keeping the underlying membrane intact. The eggshell was then removed using fine forceps, and mineral oil was applied to the membrane with a cotton bud, thereby increasing membrane transparency to allow clear visualization of the underlying veins. The samples were injected with either 30 µl of PBS as a control or 30 µl of PBS containing recombinant murine EGF (PeproTech). Different doses of EGF were injected (0.625 µg, 1.5 µg or 2 µg). Patent Blue was also added to the solution to enable visualization of the solution entering the vein during injection. Injections were undertaken using a Hamilton syringe attached to a micromanipulator (MM33 right, Marzhauser). Once injected, the eggs were cleaned to remove excess mineral oil, and the eggshell window was covered with adhesive tape. Treated embryos were then returned to their incubator. The samples were each injected three times over the course of 10 days for each experiment (Fig. 2a). At collection, the embryos were treated with an intravenous injection of EdU to label proliferating cells (Baseclick); embryo collection and fixation were undertaken 3 h after EdU injection. Some EGF-treated embryos were used for nanoindentation at the end of the experiment, and some others were incubated until hatching. Embryos were subsequently fixed in 10% NBF at 4 °C and imaged with a Keyence VHX 7000 digital microscope. Every embryo injected with EGF exhibited modified head-scale patterning. All of the replicates from these experiments are shown in Supplementary Fig. 4 and are summarized in Supplementary Table 1.

The drug that we use here (EGF) has the remarkable property of specifically promoting epidermal growth and differentiation without exhibiting strong deleterious effects in other aspects of in vivo embryonic development. Further validation of the parameters involved in the compression-folding process of crocodile head-scale patterning will require the identification of other drugs that would specifically affect one parameter at the time. For example, it would be particularly interesting to pharmacologically perturb the 3D architecture of collagen in developing crocodile embryos to investigate the corresponding effects on skin folding of the dorsal versus lateral upper jaw surface. Unfortunately, drugs currently known to effect collagen organization (such as β-aminoproprionitrile, BAPN) are highly toxic in vivo as they strongly affect the development of multiple connective tissues such as skin, bones and blood vessels. Given the great difficulties of experimentation with crocodile embryos, the screening of drugs that could, in vivo, specifically affect one mechanical parameter at a time in the skin, could be initially performed in a more classical model (such as the chicken) with more reliable source of embryos.

LSFM

The upper and lower jaws of fixed embryonic crocodile samples were dissected, dehydrated into methanol, and bleached with hydrogen peroxide, before rehydration and permeabilization in PBS with Triton X-100 (Sigma-Aldrich) (PBST). For nuclear staining, the samples were incubated in either TO-PRO-3 iodide or YO-PRO-1 iodide (3:1,000, Thermo Fisher Scientific) for 6 h. EdU-positive cells (EdU⁺) were detected using the EdU detection kit manufacturer’s guidelines (Baseclick). The samples were then dehydrated into methanol and collagen staining was undertaken in anhydrous conditions with the same Fast Green protocol²⁵ as for confocal microscopy (see above). Samples were then cleared according to the iDISCO+ protocol³⁷. Upper and lower jaw samples were imaged separately using a light-sheet microscope (Ultramicroscope Blaze, Miltenyi Biotec). Selected specimens were restained with Alizarin Red in potassium hydroxide (KOH) and re-imaged to visualize the developing calcified bone matrix (Extended Data Fig. 1b). Image stacks were processed using ImageJ³⁸, before rendering with the Redshift engine of Houdini (SideFX) and the Unreal Engine (Epic Games). A summary of replicates used for LSFM is shown in Supplementary Table 5. Each sample includes both upper and lower jaws, which we scanned separately.

3D reconstructions of hatched crocodiles

Using our custom-built imaging system³⁹, combining a robotic arm, high-resolution camera and illumination basket of light-emitting diodes, we combine ‘photometric stereo’ and ‘structure from motion’ to reconstruct the precise 3D surface mesh and colour-texture of hatched crocodile heads (Fig. 5b–e and Extended Data Fig. 6a–d). To compare the polygonal scale sizes among individuals, we first compute the minimum principle curvature of the meshes. Then, the folding network of each sample is computed by applying a skeletonization algorithm⁴⁰, followed by graph simplification (using MATLAB R2021a), on the negative curvature regions of the mesh. Using the colour texture of meshes, the folding networks were manually completed and cleaned using Houdini (SideFX).

Segmentation of LSFM data

Using TO-PRO-3, YO-PRO-1, EdU, Alizarin Red and Fast Green staining (see above), we segmented the light-sheet microscopy data to extract (in both the upper and lower jaws) the geometry of the epidermis, dermis and bone tissues (Supplementary Video 6), as well as the dominant orientations of the dermal collagen fibres, and the distribution of proliferating cells in the dermis and epidermis. The segmented data were used to build a finite element model (FEM, see below) of the crocodile head.

Cell nuclei staining signal enables precise segmentation of the epidermis from the dermis because the former exhibits a higher cell density (Fig. 3a). More specifically, the 3D image generated by LSFM on the basis of the TO-PRO-3/YO-PRO-1 fluorescence signal was subjected to 3D Canny’s edge detection⁴¹ in MATLAB-R2021a, generating a 3D binary image in which non-zero voxels form point clouds corresponding to two 3D surfaces: the surface of the epidermis and the epidermis–dermis boundary. For each of these two surfaces, we compute at each point the surface normal vector from the intensity gradient. The position of points and their corresponding normal vectors are then fed to a screened Poisson surface reconstruction algorithm⁴² in Meshlab⁴³ to reconstruct triangular surface meshes, which effectively represent the initial point clouds in a much lighter format: 3D meshes are much easier to manipulate, for example, with the Laplacian smoothing algorithm to filter out the artifactual stair-step patterns in the original voxelized data format. The epidermis surface and the epidermis–dermis boundaries allow for computing the epidermis thickness across each control and treated sample at different developmental stages.

Collagen network 3D architecture is likely to become instrumental in biomechanical modelling^25,26 because it endows tissues with distinctive mechanical properties such as anisotropic response to homogeneous stress. Thus, we assess the orientation(s) of collagen fibres in the dermis across the face and jaws of developing crocodile embryos (Fig. 3b). To this end, we use our recently published whole-mount Fast Green staining method, which provides unmatched visualization of 3D collagen network architecture via confocal or light-sheet microscopy²⁵. In brief, (1) the two most dominant orientation(s) of populations of collagen fibres were identified by determining the dominant 3D Fast Fourier transform coefficients in each of 13,000 homogeneously distributed dermal samples (cubic patches of 50 × 50 × 50 voxels) of 3D light-sheet images (Supplementary Note 1); (2) smoothing of the spatial variation of fibres orientations was achieved with an exact optimization procedure using a fibre axis mismatch energy functional (Supplementary Note 2); and (3) the two dominant fibre orientations, both tangential to the dermis mid-plane, were interpolated using spectral least-squares approximation (Supplementary Note 3).

After standard EdU labelling and detection (Supplementary Video 3), we used a 3D principal curvatures approach³⁶ (on the fluorescence signal) to segment proliferating cells in the jaws of an embryonic crocodile at E51, that is, at the onset of head-scale emergence (Fig. 3c). This approach is highly efficient for individually segmenting cells when they are grouped (that is, in contact). As the signal intensity is embedded in a 3D domain, three signal principal curvatures k_1,2,3 are computed (in MATLAB) for each voxel, and voxels characterized by k_s > k_threshold, where \({k}_{s}={({k}_{1}^{+}{k}_{2}^{+}{k}_{3}^{+})}^{\frac{1}{3}}\) and \({k}_{i}^{+}=\max ({k}_{i},0)\) are stored. The centroid of the connected voxels is considered as the location of an EdU⁺ cell. We then compute the density of EdU⁺ cells, separately for the dermis and the epidermis, by choosing sampling points in the corresponding segmented tissue layers. The space surrounding each sampling point is limited to a box of 80 × 80 × 80 voxels clipped by the layer boundaries. The density of EdU⁺ cells at a sampling point is computed as the number of cells inside the clipped box divided by its volume. In our numerical model, densities of proliferating cells are represented as a space-dependent growth function. We transfer this information to the 3D model using a spectral least-squares approximation approach to interpolate data on the spatial modes of the target mesh (details are provided in Supplementary Note 3).

For segmenting bone tissue, we use either the 3D Canny’s edge detection of the (very strong) Alizarin Red signal or a semi-automatic procedure for samples with (weaker) Fast Green or EdU signals. In the latter case, we (1) choose several sections in the x, y and z directions and manually mark the separation between the dermis and the bone, (2) store the coordinates of all profile points as a 3D point cloud and compute their normal with Variational Implicit Point Set Surface⁴⁴ and (3) use screened Poisson surface reconstruction⁴² from Meshlab⁴³ to generate the mesh corresponding to the bone surface.

A biomechanical model of head-scale emergence

We use the segmented data to build a 3D finite-element numerical growth model. Triangular meshes were generated, both for upper and lower jaws, at the surface boundaries of the epidermis, dermis and bone of embryos before the onset of head-scale patterning (Fig. 1b and see above). The epidermis surface and the epidermis–dermis interface were smoothed to remove any artificial local deformations associated with sample preparation, including dehydration into methanol. The 3D volume of each of the three layers was represented as a tetrahedral mesh generated with TetGen⁴⁵ (Extended Data Fig. 8a).

During simulated growth, the deformation of tetrahedral elements is realized through finite-strain theory in which the bulk material configuration at current time t is represented as the spatial coordinates of a collection of points in the form of a vector variable x = x(X,t), where X is the spatial coordinates of these points at a reference configuration, that is, at t = 0 (Extended Data Fig. 8b). The coordinates between the current and the reference configurations are connected by the deformation gradient map, F—that is, a second-order tensor that incorporates the elastic and growth deformations. The elastic energy and the mechanical stress stored in each tetrahedral element is then calculated from the neo-Hookean material model, known to behave appropriately under large deformations^30,31,46, and allowing the incorporation of anisotropic material, such as collagen fibres⁴⁷ (Supplementary Note 4). The direction of fibres, as well as the spatial pattern of cell proliferation density, both inferred from LSFM data (Fig. 3b,c), are fed to the mechanical model. However, the elastic moduli, fibre stiffness and final amount of growth are considered as unknown parameters. Note that the absolute values of stiffness are irrelevant in the numerical simulations as the model key parameters are the fibre stiffness relative to the dermis and epidermis moduli, as well as the ratio of epidermis to dermis stiffnesses (Young’s moduli).

Numerical simulations and parameter optimization

To perform numerical simulations, the mechanical model formulation described above is discretized for tetrahedral elements using the FEM and integrated with contact and viscous forces (Supplementary Note 5). The final model is then implemented in an in-house application that uses NVIDIA GPUs for high-performance computation. For that purpose, we used the CUDA programming language to develop intensive-computation kernels, whereas C++ is used for data management, geometry processing, input/output operations and the graphical user interface. Our application integrates the following open-source libraries: Dear ImGui (https://github.com/ocornut/imgui, MIT licence) for the graphical user interface, CUDA C++ Core Libraries (https://github.com/NVIDIA/cccl, Apache-2.0, FreeBSD, BSD-3-Clause licences) for parallel algorithms, Eigen (https://gitlab.com/libeigen/eigen, MPL-2.0, BSD licences) for linear algebra and libigl (https://github.com/libigl/libigl, GPL-3.0, MPL-2.0 licences) for geometry processing. The simulation input is a tetrahedral mesh that defines the geometry of the crocodile head (epidermis, dermis and bone layers). Moreover, a set of model parameters are used: in addition to the dermal collagen fibres orientation and stiffness, we include, both for epidermis and dermis, the Young’s modulus and Poisson’s ratio, the growth rate functions and the cell proliferation pattern. The deformation of the skin is then computed and the final geometry is generated as a tetrahedral mesh.

The mechanical model is integrated with a Bayesian optimization process (bayesopt library from MATLAB R2021a with parallel sampling), that is, a machine-learning global minimization algorithm. The optimality criterion consists of the distance between the metrics (integrating multiple topological and geometrical features, see below) of the steady-state simulated geometry versus LSFM-acquired meshes. To compute the metrics of a folding network, we first compute the minimum principle curvature of the corresponding surface mesh representing the epidermis boundary. We then segment the skin folds by applying a skeletonization algorithm⁴⁰, followed by graph simplification (using MATLAB R2021a), on the negative curvature regions of the mesh. Next, we compute the following geometrical and topological features of the network: number of domains (cycles), perimeters of domains, lengths of edges, curvatures of edges and lengths of incomplete edges. The final metrics is a vector of which the components are the means of these features, normalized to the diagonal length of its bounding box. Given that components within a metrics vector may differ significantly among each other, we need to normalize them properly. For this purpose, we use LSFM data to compute the metrics of controls at E64 and treated individuals (2 μg EGF) at E64. We then compute the interindividual (that is, among all individuals) mean and s.d. of each component (Fig. 2e). We finally normalize the components of any newly computed metrics by subtracting the interindividual mean and dividing by the interindividual s.d.

Finding optimal parameter values for control and treated targets is performed in two steps. First, we use an E64 control target mesh and perform optimization on the six-dimensional parameter space, including epidermis Young’s modulus, E_epidermis (keeping E_dermis = 1); epidermis and dermis Poisson’s ratios, v_{epidermis/dermis}; dermis tangential growth values, \({G}_{T,{\rm{dermis}}}^{+/-}\) (keeping \({G}_{T,{\rm{epidermis}}}^{+/-}\) at 80% of the dermis values); and the fibre stiffness, k₁ (k₂ being set to 0). Second, using a 2 μg EGF-treated target, we perform another optimization on the three-dimensional parameter space including epidermis-related parameters, that is, E_epidermis, v_epidermis and \({\lambda }_{T,{\rm{epidermis}}}^{{\rm{EGF}}}\) (additional epidermal tangential growth induced by EGF). See Supplementary Notes 4 and 6 for the definitions of parameters and Supplementary Table 4 for the complete list of parameter values. To minimize the distance between the metrics vectors of the simulated versus LSFM target geometry (control or treated), we use a Gaussian process (that is, a generalization of the multivariate normal distribution to infinite dimensions) in the optimization loop to approximate posterior mean and variance functions from which the objective function is sampled (Extended Data Fig. 8d). The posterior functions are updated at each iteration according to Bayesian inference and this information is then used to compute the expectation of the improvement function, which measures the chance of observing an objective (that is, the distance between simulation and observation) smaller than the minimum objective observed so far (Supplementary Note 7). The optimization process, which typically takes a few thousand iterations, continues until no more improvement is observed in the last 500 iterations.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.