Search for light sterile neutrinos with two neutrino beams at MicroBooNE

A broad experimental programme has shown that the three quantum-mechanical eigenstates of neutrino flavour, ν_e, ν_μ and ν_τ, are related to the three eigenstates of neutrino mass, ν₁, ν₂ and ν₃, by the unitary Pontecorvo–Maki–Nakagawa–Sakata (PMNS) matrix^11,12. This mixing between flavour and mass states gives rise to the phenomenon of neutrino oscillation, in which neutrinos transition between flavour eigenstates with a characteristic wavelength in \(L/{E}_{\nu }\propto {(\Delta {m}_{ji}^{2})}^{-1}\), where L is the distance travelled by the neutrino, E_ν is the neutrino energy and \(\Delta {m}_{ji}^{2}={m}_{j}^{2}-{m}_{i}^{2}\) is the difference between the squared masses of the mass eigenstates ν_i and ν_j. The three known neutrino mass states give rise to two independent mass-squared differences and thus to two characteristic oscillation frequencies that have been well measured with neutrinos from nuclear reactors^13,14, the Sun¹⁵, the atmosphere of Earth^16,17 and particle accelerators^18,19,20.

In apparent conflict with the three-neutrino model, several experiments during the past three decades have made observations that can be interpreted as neutrino flavour change with a wavelength much shorter than is possible given only the two measured mass-squared differences^{3,4,5,6,7,8,9}. These observations are often explained as neutrino oscillations caused by at least one additional mass state, ν₄, corresponding to a mass-squared splitting of \(\Delta {m}_{41}^{2}\gtrsim 1{0}^{-2}\,{{\rm{eV}}}^{2}\), which is much greater than the measured \(\Delta {m}_{21}^{2}\) and \(\Delta {m}_{32}^{2}\). New mass states would require the addition of an equivalent number of new flavour states, in conflict with measurements of the Z-boson decay width²¹, which have definitively shown that only three light neutrino flavour states couple to the Z boson of the weak interaction. Therefore, these additional neutrino flavour states must be unable to interact through the weak interaction and are thus referred to as ‘sterile’ neutrinos. In this analysis, we focus specifically on light sterile neutrinos—those with masses below at least half the mass of the Z boson. It should be noted that the term ‘sterile neutrino’ has also been used to describe new particles, such as heavy right-handed lepton partners, that are potentially more massive than the Z boson. However, our study does not directly test these scenarios. The discovery of additional neutrino states would have profound implications across particle physics and cosmology, for example, on our understanding of the origin of neutrino mass, the nature of dark matter and the number of relativistic degrees of freedom in the early universe.

With the addition of a single new mass state ν₄ and a single sterile flavour state ν_s, the PMNS matrix becomes a 4 × 4 unitary matrix described by six real mixing angles θ_ij (1 ≤ i < j ≤ 4). Oscillations driven by the two measured mass-squared splittings have not had time to evolve for small values of L/E_ν. The ν_μ to ν_e flavour-change probability, \({P}_{{\nu }_{{\rm{\mu }}}\to {\nu }_{{\rm{e}}}}\), and the ν_e and ν_μ survival probabilities, \({P}_{{\nu }_{{\rm{e}}}\to {\nu }_{{\rm{e}}}}\) and \({P}_{{\nu }_{{\rm{\mu }}}\to {\nu }_{{\rm{mu}}}}\), can then, to a very good approximation, be described by

where θ_ee ≡ θ₁₄, \({\sin }^{2}(2{\theta }_{{\rm{\mu \mu }}})\equiv 4{\cos }^{2}{\theta }_{14}{\sin }^{2}{\theta }_{24}(1-{\cos }^{2}{\theta }_{14}{\sin }^{2}{\theta }_{24})\) and \({\sin }^{2}(2{\theta }_{{\rm{\mu e}}})\equiv {\sin }^{2}(2{\theta }_{14}){\sin }^{2}{\theta }_{24}\), following the common parameterization²². Flavour transitions due to these new oscillation parameters are experimentally probed by observing unexpected deficits or excesses in charged current (CC) ν_e and ν_μ interactions in a flavour-sensitive neutrino detector from a source of well-defined neutrino flavour content.

Observations compatible with a fourth neutrino mass state have been made in measurements of intense electron-capture decay sources^6,7,8, in which a deficit in detected ν_e rates implies non-unity \({P}_{{\nu }_{{\rm{e}}}\to {\nu }_{{\rm{e}}}}\) from a \(\Delta {m}_{41}^{2} > {\mathcal{O}}(1\,{{\rm{eV}}}^{2})\). Although a hint of non-unity \({P}_{{\overline{\nu }}_{{\rm{e}}}\to {\overline{\nu }}_{{\rm{e}}}}\) is provided by the nuclear-reactor-based Neutrino-4 experiment⁹, this result is in conflict with other reactor-based observations from DANSS, NEOS, PROSPECT and STEREO, which see no evidence for L/E_ν-dependent \({\overline{\nu }}_{{\rm{e}}}\) disappearance^23,24,25,26. Two accelerator-based experiments, LSND and MiniBooNE, have observed potential evidence of non-zero \({P}_{{\nu }_{{\rm{\mu }}}\to {\nu }_{{\rm{e}}}}\) associated with large mass splittings of \(\Delta {m}_{41}^{2} > {\mathcal{O}}(1{0}^{-2}\,{{\rm{e}}{\rm{V}}}^{2})\). The LSND experiment observed an anomalous excess of \({\overline{\nu }}_{{\rm{e}}}\) interactions in a π⁺ decay-at-rest beam³. The MiniBooNE experiment, situated downstream from the Booster Neutrino Beam (BNB) proton target facility generating a beam of GeV-scale ν_μ and \({\overline{\nu }}_{{\rm{\mu }}}\) from decays of boosted π⁺ and π⁻, observed an excess of electromagnetic showers indicative of ν_e interactions that would imply a non-zero \({P}_{{\nu }_{{\rm{\mu }}}\to {\nu }_{{\rm{e}}}}\) (refs. ^4,5). Observations of ν_e disappearance and ν_e appearance should be accompanied by ν_μ disappearance (non-unity \({P}_{{\nu }_{{\rm{\mu }}}\to {\nu }_{{\rm{\mu }}}}\)) if the PMNS matrix is unitary. No conclusive observation of this ν_μ disappearance has been reported^27,28,29. The overall picture of the existence and phenomenology of sterile neutrino states thus remains inconclusive.

In this article, we present new results on sterile neutrino oscillations from the MicroBooNE liquid-argon time projection chamber (LArTPC) experiment at Fermilab¹⁰. Situated along the same BNB beamline hosting the MiniBooNE experiment, MicroBooNE was conceived to directly test the non-zero \({P}_{{\nu }_{{\rm{\mu }}}\to {\nu }_{{\rm{e}}}}\) observation of MiniBooNE. By supplanting the Cherenkov detection technology of MiniBooNE with the precise imaging and calorimetric capabilities of a LArTPC, MicroBooNE can reduce backgrounds and select a high-purity sample of true ν_e-generated final-state electrons. The first ν_e measurement results of MicroBooNE using differing final-state topologies showed no evidence for an excess of ν_e-generated electrons from the BNB^30,31,32,33. These results were used to set limits on ν_μ → ν_e flavour transitions, excluding sections of the region in \((\Delta {m}_{41}^{2},{\sin }^{2}(2{\theta }_{{\rm{\mu e}}}))\) space favoured by LSND and MiniBooNE data³⁴. As the BNB has an intrinsic contamination of electron neutrinos, the disappearance of electron neutrinos can cancel the appearance of electron neutrinos from ν_μ → ν_e oscillations³⁵. This effect leads to a degeneracy between the impact of the mixing angles θ_μe and θ_ee of equations (1) and (2) that weakens the sensitivity to the parameters of the expanded 4 × 4 PMNS matrix.

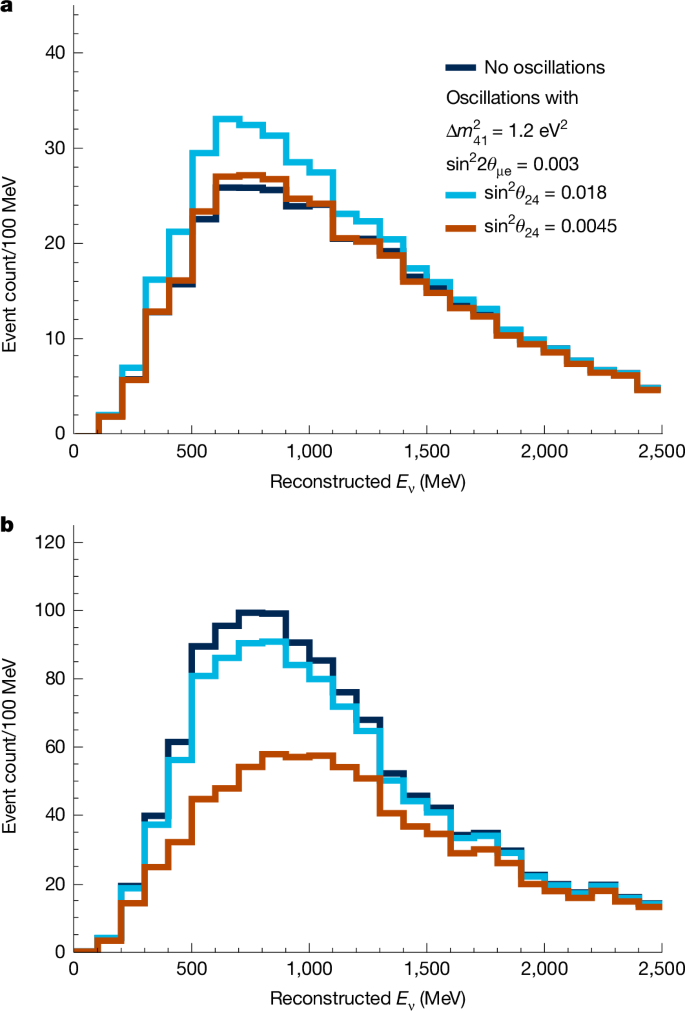
We overcome the limitations of the degeneracy between ν_e appearance and ν_e disappearance by performing one of the first oscillation searches using two accelerator neutrino beams: the BNB and the Neutrinos at the Main Injector (NuMI) beam. The MicroBooNE detector is aligned with the direction of BNB and is at an angle of about 8° relative to the NuMI beam. Beam timing information is used to distinguish and record events from each beam separately. This configuration results in two neutrino datasets differing in the intrinsic electron-flavour fraction. The electron-flavour content of BNB is 0.57% and that of the NuMI beam is 4.6%. These two independent sets of data, with substantially different electron-flavour contents, break the degeneracy between ν_e appearance and disappearance. We show the impact of using two beams in Fig. 1a,b, in which we compare simulated ν_e energy spectra from the BNB and the NuMI beam for the three-flavour (3ν) hypothesis and for two sets of parameters of the expanded four-flavour (4ν) PMNS model with \(\Delta {m}_{41}^{2}=1.2\,{{\rm{e}}{\rm{V}}}^{2}\) and \({\sin }^{2}(2{\theta }_{{\rm{\mu e}}})=0.003\). For \({\sin }^{2}{\theta }_{24}=0.0045\) the ν_e appearance and disappearance cancel in the BNB, leaving a ν_e spectrum that is almost identical to the 3ν case, whereas the NuMI beam shows an indication of ν_e disappearance. The appearance and disappearance effects almost fully cancel in the NuMI beam for \({\sin }^{2}{\theta }_{24}=0.018\), whereas the BNB shows a clear indication of ν_e appearance. In the Methods, we provide further discussion of this degeneracy over a broader range of mass-squared splittings and mixing angles.

a,b, Simulated reconstructed energy spectra of FC CC ν_e interactions in MicroBooNE from the BNB (a) and the NuMI beam (b). The dark blue histograms show the 3ν expectation for \({\sin }^{2}{\theta }_{24}={\sin }^{2}(2{\theta }_{{\rm{\mu e}}})=0\). The light blue and red histograms show expectations for two sets of parameters of the 4ν model, both with \(\Delta {m}_{41}^{2}=1.2\,{{\rm{e}}{\rm{V}}}^{2}\) and \({\sin }^{2}(2{\theta }_{{\rm{\mu e}}})=0.003\). The light blue histograms show the expectation for \({\sin }^{2}{\theta }_{24}=0.018\) and the red histograms show the expectation for \({\sin }^{2}{\theta }_{24}=0.0045\). Note that these parameters were chosen specifically to highlight differences in the oscillated spectra between BNB and NuMI and do not imply that parameter spaces associated with these values are newly excluded by this result.

Using the two-beam technique, this new MicroBooNE analysis achieves marked improvements in sensitivity to the parameters \({\sin }^{2}(2{\theta }_{{\rm{ee}}})\) and \({\sin }^{2}(2{\theta }_{{\rm{\mu e}}})\) relative to MicroBooNE’s prior sterile neutrino analysis over a broad range of \(\Delta {m}_{41}^{2}\) values. These improvements are shown by the sensitivities presented in Extended Data Fig. 2. The results presented here using two neutrino beams place robust new constraints on the validity of the sterile neutrino hypothesis in explaining existing short-baseline anomalies in neutrino physics. This analysis strengthens the direct test of the sterile neutrino interpretation of the MiniBooNE anomaly and allows MicroBooNE to probe the \({\sin }^{2}(2{{\theta }}_{{\rm{\mu }}{\rm{e}}})\) parameter space favoured by LSND. We also constrain \({\sin }^{2}(2{\theta }_{{\rm{ee}}})\), complementing existing exclusions from reactor, solar^36,37 and β-decay³⁸ experiments, thereby further restricting the sterile neutrino parameter space relevant to the gallium anomaly.

We use data corresponding to 6.369 × 10²⁰ protons on target (POT) in the BNB, with magnetic van der Meer horns configured to focus positively charged hadrons, leading to a ν_μ-dominated beam with a 5.9% \({\overline{\nu }}_{{\rm{\mu }}}\) component and a 0.57% \({\nu }_{{\rm{e}}}+{\overline{\nu }}_{{\rm{e}}}\) component. From the NuMI beam, a total of 10.54 × 10²⁰ POT are used, in which 30.8% were taken with horns configured to focus positively charged hadrons and the remainder with horns focusing negatively charged hadrons. The NuMI flux observed in the MicroBooNE detector, with both horn configurations combined, is ν_μ dominated with a 42.1% \({\overline{\nu }}_{{\rm{\mu }}}\) component and a 4.6% \({\nu }_{{\rm{e}}}+{\overline{\nu }}_{{\rm{e}}}\) component. In the rest of this paper, we do not discriminate between neutrinos and antineutrinos and refer to the \({\nu }_{{\rm{\mu }}}+{\overline{\nu }}_{{\rm{\mu }}}\) and \({\nu }_{{\rm{e}}}+{\overline{\nu }}_{{\rm{e}}}\) samples as ν_μ and ν_e samples for brevity. For both BNB and NuMI, the POT used in this analysis represent roughly half of the total data collected by the MicroBooNE detector; additional data remain available for future studies.

The LArTPC detector of MicroBooNE has an active volume of 10.4 × 2.6 × 2.3 m³ containing 85 tonnes of liquid argon. Charged particles passing through the argon create ionization trails. A 273 V cm⁻¹ electric field drifts the ionization electrons towards an anode plane consisting of three layers of wires separated by 3 mm and each with a 3-mm wire pitch that collects the electrons and enables three-dimensional imaging of the neutrino interactions. The passage of charged particles through the argon also produces scintillation light that is collected by a system of photomultiplier tubes to provide timing information. Signal processing and calibrations of MicroBooNE data are described in refs. ^{39,40,41,42,43,44}.

Neutrino interactions in the LArTPC are reconstructed with the Wire-Cell analysis framework⁴⁵. The techniques for identifying and reconstructing neutrino interactions and their energies have been described elsewhere³³. We select a sample of CC ν_e interactions from the BNB (NuMI beam) with 82% (91%) purity and 46% (42%) efficiency, and a sample of CC ν_μ interactions with 92% (78%) purity and 68% (62%) efficiency. The CC ν_e and CC ν_μ samples are divided into fully contained (FC) and partially contained (PC) samples, depending on whether all charge depositions are contained in a fiducial volume 3 cm within the TPC boundary. The CC ν_μ events that contain a reconstructed π⁰ are separated into two additional FC and PC samples per beam. Neutral current (NC) interactions that produce a π⁰ are distinguished by the absence of a long muon-like track and the presence of detached reconstructed electromagnetic showers. These form an additional sample. In total, we define 14 distinct event categories, seven for each beam.

We produce a Monte Carlo prediction of our 14 samples, to which we compare the data. There is substantial systematic uncertainty creating this Monte Carlo simulation. The uncertainty on the predicted rates of the 14 samples is given in Table 1 and is referred to as the unconstrained systematic uncertainty. The largest uncertainties come from neutrino interaction modelling for the BNB samples and from a combination of neutrino flux and interaction uncertainties for the NuMI samples. Many of these uncertainties are highly correlated. Thus, a combined fit of all samples effectively constrains the uncertainties on the CC ν_e prediction and at the same time allows the CC ν_e prediction to be modified, as can be seen from Table 1. The pionless samples constrain uncertainties on CC ν_e signal events, whereas the π⁰ samples constrain uncertainties on the dominant background.

Uncertainties on the neutrino flux prediction arise from uncertainties in the production of charged pions and kaons in the BNB and NuMI targets and the material around the target halls and hadron-decay volumes. These uncertainties are evaluated through comparison with external hadron production data^46,47,48, following a procedure similar to that described in ref. ⁴⁹. The ν_e flux from three-body K and μ decays is highly correlated with the ν_μ flux from two-body π and K decays, allowing our ν_μ samples to effectively constrain the uncertainties on the ν_e flux predictions. The neutrino interaction model is tuned using datasets of pionless CC interactions from the T2K experiment⁵⁰. Uncertainties on this neutrino interaction model are evaluated by varying the input parameters within their allowed uncertainties. These uncertainties are correlated between the BNB and NuMI datasets and between the CC ν_μ and ν_e samples because of the lepton universality of the weak interaction. Uncertainties on the simulation of the detector include uncertainties on the response of the detector to ionization, uncertainties on the amount of ionization charge freed by passing charged particles through the detector, uncertainties on the electric field map of the TPC, uncertainties on the production and propagation of scintillation light, uncertainties on backgrounds from interactions occurring outside the cryostat, and uncertainties on finite statistics of the simulation samples used for predictions.

The simultaneous fit to the 14 samples from the BNB and the NuMI beam incorporates all sources of systematic uncertainty through a covariance matrix. We allow \({\sin }^{2}(2{\theta }_{{\rm{\mu e}}})\), \({\sin }^{2}(2{\theta }_{{\rm{ee}}})\) and \(\Delta {m}_{41}^{2}\) complete freedom within unitarity bounds as parameters of the fit. The covariance-matrix formalism χ² test of the fit can be found in the Methods. The constrained predictions shown in Fig. 2 assume the 3ν hypothesis of \({\sin }^{2}(2{\theta }_{{\rm{\mu e}}})={\sin }^{2}(2{\theta }_{{\rm{ee}}})=0\). They agree well with the data, with a P-value of 0.92. The best-fit values for the oscillation parameters in the 4ν hypothesis are \(\Delta {m}_{41}^{2}=1.30\times 1{0}^{-2}\,{{\rm{e}}{\rm{V}}}^{2}\), \({\sin }^{2}(2{\theta }_{{\rm{\mu e}}})=0.999\), and \({\sin }^{2}(2{\theta }_{{\rm{ee}}})=0.999\), with a χ² difference with respect to the 3ν hypothesis of

We observe no marked preference for the existence of a sterile neutrino with a P-value of 0.96 evaluated using the Feldman–Cousins procedure.

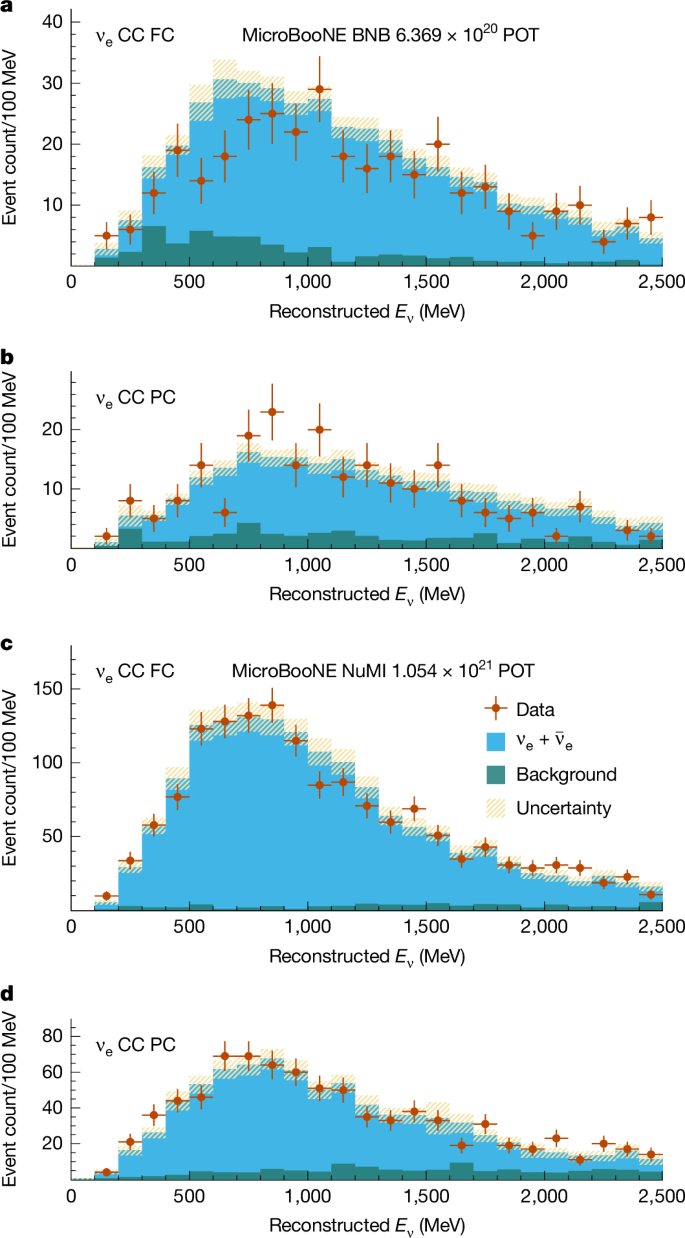
a–d, Reconstructed energy spectra of events selected as FC CC ν_e candidates in the BNB (a), PC CC ν_e candidates in the BNB (b), FC ν_e candidates in the NuMI beam (c) and PC ν_e candidates in the NuMI beam (d). The data points are shown with statistical error bars. The constrained predictions for each sample are shown for the 3ν hypothesis as the solid histograms, with the blue showing the true CC ν_e events and the green showing the background events. The background category contains CC ν_μ interactions, NC neutrino interactions, cosmic rays and interactions occurring outside the fiducial volume of the detector. The yellow band shows the total constrained systematic uncertainty on the prediction.

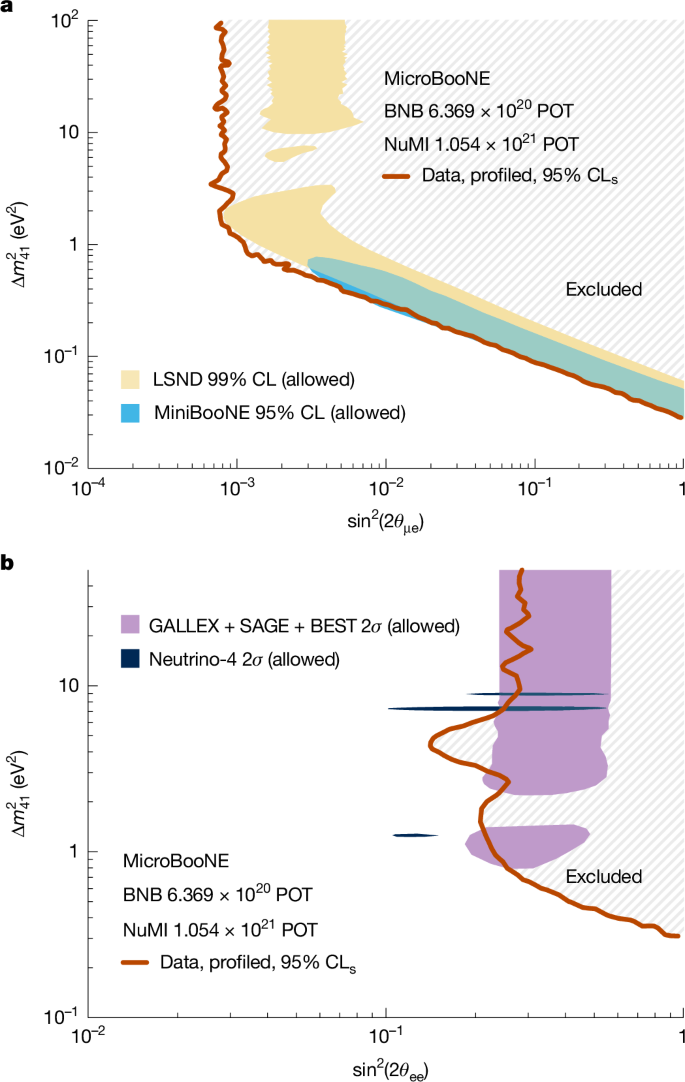
Exclusion contours are calculated using the frequentist CL_s (confidence level as a function of s) method⁵¹. The exclusion contour in any two-dimensional parameter space is obtained by profiling the third free parameter. At any point in the two-dimensional space, the value of the profiled parameter that minimizes the χ² with respect to the data is chosen. Figure 3a shows the 95% CL_s exclusion contour in the \((\Delta {m}_{41}^{2},{\sin }^{2}(2{\theta }_{{\rm{\mu e}}}))\) parameter space. The region allowed at 99% CL by the LSND measurement and the vast majority of the region allowed at the 95% CL by the MiniBooNE experiment are excluded. Figure 3b shows the 95% CL_s exclusion contour in the \((\Delta {m}_{41}^{2},{\sin }^{2}(2{\theta }_{{\rm{ee}}}))\) parameter space. A notable portion of the region allowed by gallium measurements and part of the region derived from the Neutrino-4 measurement are excluded. In the Methods and Extended Data Fig. 2, we compare our exclusions with the expected median sensitivities.

a,b, The red lines show exclusion limits at the 95% CL_s level in the plane of \(\Delta {m}_{41}^{2}\) and \({\sin }^{2}(2{\theta }_{{\rm{\mu }}{\rm{e}}})\) (a) or \({\sin }^{2}(2{\theta }_{{\rm{e}}{\rm{e}}})\) (b). All the regions to the right of these lines are excluded by the MicroBooNE data. In a, the yellow shaded area is the LSND 99% CL allowed regions³, which neglects the degeneracy between ν_e disappearance and appearance. The light blue area is the MiniBooNE 95% CL allowed region⁵⁸, considering both ν_e disappearance and appearance. In b, the purple shaded area is the 2σ allowed region of the gallium anomaly⁵⁹. The dark blue shaded area is the 2σ allowed region from the Neutrino-4 experiment⁹. For context, note that the stronger-than-expected constraint on \({\sin }^{2}(2{\theta }_{{\rm{\mu e}}})\), driven by the deficit observed in the BNB ν_e CC FC sample and the excess in the NuMI ν_μ CC sample, is discussed in detail in the Methods and Extended Data Fig. 2.

In summary, using data from the MicroBooNE detector, we report one of the first searches for a sterile neutrino using two accelerator neutrino beams. The oscillation fit to the 4ν model using a total of 14 CC ν_e, CC ν_μ and NC π⁰ samples from the BNB and the NuMI beam in a single detector achieves a marked reduction of systematic uncertainties and a powerful mitigation of degeneracies between ν_e appearance and disappearance. The result shows no evidence of oscillations induced by a single sterile neutrino and is consistent with the 3ν hypothesis with a P-value of 0.96. We comprehensively exclude at a 95% CL the 4ν parameter space that would explain the LSND and MiniBooNE anomalies through the existence of a light sterile neutrino in a model with an extended 4 × 4 PMNS matrix. Our result expands the diverse range of experimental approaches, excluding regions that would explain the gallium anomaly and the Neutrino-4 observation with a light sterile neutrino. This work, therefore, provides a robust exclusion of a single light sterile neutrino as an explanation for the array of short-baseline neutrino anomalies observed over the past three decades, representing the strongest constraint from a short-baseline experiment using accelerator-produced neutrinos. Expanded models, including several light sterile neutrinos⁵², neutrino decay effects^53,54 or production and decay of new particles connected with the dark sector^55,56 might explain the anomalies. The Short Baseline Neutrino (SBN) Programme⁵⁷ at Fermilab adds two new LArTPC detectors in the BNB, at different distances from the proton target. Future measurements by MicroBooNE and the broader SBN Programme can shed light on this expanded model space, with future comprehensive insights provided by near-term short-baseline measurements from diverse flavour channels and energy regimes.