Scalable watermarking for identifying large language model outputs

Detailed SynthID-Text method

In this section, we provide a detailed description of SynthID-Text.

The LLM distribution

Most LLMs are autoregressive, providing the probability p_LM(x_t∣x_<t) of the next token x_t given the text so far x_<t. Text is typically generated from the LLM using an autoregressive decoding method, which optionally modifies the LLM distribution p_LM(⋅∣x_<t) before sampling from it. Such modifications include top-k and top-p³⁴ sampling, which truncate p_LM(⋅∣x_<t) to the k most likely tokens or the tokens covering the top-p probability mass; this can be combined with applying a temperature parameter τ (ref. ³⁵). Although these modifications increase or decrease the amount of entropy in p_LM(⋅∣x_<t), SynthID-Text is compatible with any autoregressive decoding method that has non-zero entropy in the modified distribution. Thus, SynthID-Text is compatible with top-k sampling for all k ≥ 2, top-p sampling for all \(p\in \left(0,1\right]\), and all temperatures τ > 0.

SynthID-Text is applied after any such modifications have been made, so for the purposes of this paper we define the LLM distribution p_LM(⋅∣x_<t) to be the distribution after any such modifications.

Definition 1 (LLM distribution)

Given an autoregressive LLM, an autoregressive decoding method, and x_<t = x₁, …, x_t−1, a sequence of tokens from the vocabulary V, the LLM distribution p_LM(⋅∣x_<t) is the probability distribution from which the decoding method samples the next token x_t ∈ V.

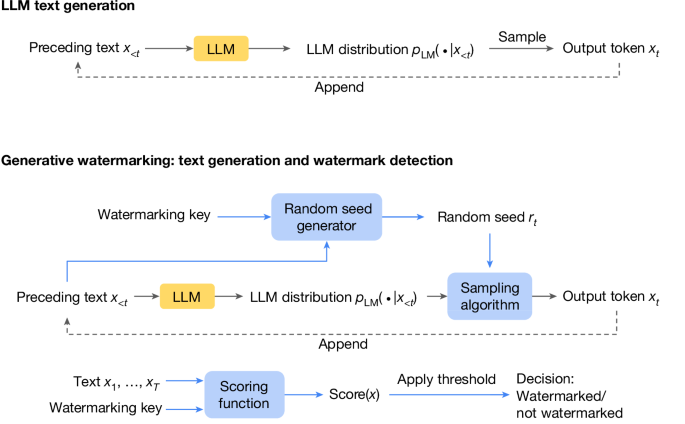
Watermarking framework

We present SynthID-Text as comprising a random seed generator, a sampling algorithm and a scoring function; this is similar to the generative watermarking framework of ref. ²¹. Intuitively, the sampling algorithm samples text from the LLM in a way that is biased by random seeds provided on each step by the random seed generator; later we can identify the watermark by detecting this bias through the scoring function. We describe the random seed generator and sampling algorithm in this section and describe several scoring functions in Supplementary Information section A. See Supplementary Information section B for a detailed discussion of related generative watermarking approaches.

Random seed generator

To generate a piece of watermarked text x₁, …, x_T, we require a sequence of random seeds \({r}_{1},\ldots ,{r}_{T}\in {\mathcal{R}}\) (where \({\mathcal{R}}\) is the space of all random seeds) to bias the sampling from the LLM distribution on each step. The random seed generator is the process by which we generate these random seeds. One approach is to make the random seed generator a deterministic function f_r that takes as input the sequence of tokens so far x_<t = x₁, …, x_t−1 and a watermarking key k and outputs a random seed \({r}_{t}:={f}_{r}({x}_{ < t},k)\in {\mathcal{R}}\). Randomizing the key k should randomize the seed; that is, for all \({x}_{ < t},{{\mathbb{P}}}_{{k \sim }\text{Unif}({\mathcal{R}})}\,[\,{f}_{r}({x}_{ < t},k)]=\text{Unif}\,({\mathcal{R}})\).

There are several possible choices for f_r (ref. ²¹); for our experiments, we use the sliding window f_r(x_<t, k) ≔ h(x_t−H, …, x_t−1, k), which is a hash function h of the last H tokens (for some context length H ≥ 1) and of the key k. This random seed generator is the same as that used by refs. ^22,23. In this work, we also assume the watermarking key k and random seed r_t exist in the same space of n_sec-bit integers, where n_sec is the security parameter.

Definition 2 (random seed space, random seed distribution)

Given a security parameter n_sec, the random seed space \({\mathcal{R}}={\{0,1\}}^{{n}_{\text{sec}}}\) is the space of all n_sec-bit integers. The random seed distribution is the uniform distribution over all such integers \(\,\text{Unif}\,({\mathcal{R}})\).

We also assume that the family of functions \({\{h(\cdot ,\ldots ,\cdot ,k)\}}_{k\in {\mathcal{R}}}\) is a pseudorandom function family, meaning that (1) h(x_t−H, …, x_t−1, k) is efficiently computable for any x_t−H, …, x_t−1 and k, and (2) the distribution of \({\{h(\cdot ,\ldots ,\cdot ,k)\}}_{{k \sim }\text{Unif}({\mathcal{R}})}\) is computationally indistinguishable from a function sampled uniformly randomly from the set of all functions from V^H to \({\{0,1\}}^{{n}_{\text{sec}}}\).

g-values

As illustrated in Fig. 2, Tournament sampling requires g-values to decide which tokens win each match in the tournament. Intuitively, we want a function that takes a token x ∈ V, a random seed \(r\in {\mathcal{R}}\) and the layer number ℓ ∈ {1, …, m}, and outputs a g-value g_ℓ(x, r) that is a pseudorandom sample from some probability distribution f_g (the g-value distribution).

For example, in Fig. 2, the g-value distribution is Bernoulli(0.5). Given the random seed r, g_ℓ(x, r) produces pseudorandom g-values of 0 or 1 for each token x in the vocabulary, for each layer ℓ = 1, 2, 3. In this paper, we primarily use the Bernoulli(0.5) g-value distribution, although we also explore Uniform[0, 1]. In general, any g-value distribution can be chosen, as a hyperparameter of the Tournament sampling method.

Definition 3 (g-value distribution)

The g-value distribution is a probability distribution of any real-valued random variable. We write F_g to denote the cumulative distribution function, and f_g to denote the probability density function (if continuous) or probability mass function (if discrete).

Next, we need a way to produce a hash \(h(x,{\ell },r)\in {\mathcal{R}}\) of a token x ∈ V, an integer ℓ ∈ {1, …, m} and a random seed \(r\in {\mathcal{R}}\). Let’s assume we have a pseudorandom function family \({\{h(\cdot ,\cdot ,r)\}}_{r\in {\mathcal{R}}}\) similar to the one described in the ‘Random seed generator’ section, such that the distribution of \({\{h(\cdot ,\cdot ,r)\}}_{{r \sim }{\rm{Unif}}({\mathcal{R}})}\) is computationally indistinguishable from a function sampled uniformly randomly from the set of all functions from V × [m] to \({\{0,1\}}^{{n}_{\sec }}\).

Definition 4 (g-value)

Given a g–value distribution with cumulative density function. F_g, a random seed \(r\in {\mathcal{R}}\), and integer ℓ ∈ 1, …, m, the layer-ℓ g-value of a token x ∈ V is given by:

where \({F}_{g}^{-1}\) is the generalized inverse distribution function of F_g, and h is a hash function as described above.

Intuitively, Definition 4 says that we take a hash h(x, ℓ, r) of x, â„“ and r, which gives us a uniformly distributed n-bit integer, and divide it by 2ⁿ to get a number in [0, 1]. For large n, this converges to a uniformly distributed number in [0, 1]. We then perform inverse transform sampling to turn this number into a sample from the g-value distribution given by F_g.

Tournament sampling algorithm

Definition 5 (watermarking sampling algorithm)

In a watermarking scheme, a sampling algorithm \({\mathcal{S}}:\Delta V\times {\mathcal{R}}\to V\) is an algorithm that takes as input a probability distribution p ∈ ΔV and a random seed \(r\in {\mathcal{R}}\) and returns a token \({\mathcal{S}}(p,r)\in V\). If \({\mathcal{S}}\) always returns the same token given the same p and r, it is deterministic. Otherwise, \({\mathcal{S}}\) is probabilistic.

We propose a new probabilistic sampling algorithm called Tournament sampling. We present the simplest, single-layer version of Tournament sampling in Algorithm 1. Instead of sampling directly from p_LM(⋅∣x_<t), we sample N tokens from p_LM(⋅∣x_<t), compute their g-values as described in the previous section and choose uniformly among those that have the maximal g-value.

Algorithm 2 presents the full multilayer version of Tournament sampling, which has an additional hyperparameter m, the number of layers. The process can be thought of as a knockout tournament with m stages, where each match is an instantiation of the single-layer algorithm; this continues until there is one winner. Importantly, each layer ℓ of the tournament uses different g-values g_ℓ(⋅, r_t) to decide the winners. Figure 2 gives a concrete example for m = 3 layers, N = 2 samples and a Bernoulli(0.5) g-value distribution.

Algorithm 1

Sampling a token with single-layer Tournament sampling

Require: LLM distribution p_LM(⋅∣x_<t), random seed \({r}_{t}\in {\mathcal{R}}\), number of samples N ≥ 2, g function with g-value distribution f_g (see Definition 4).

1: Draw Y = [y₁, y₂, â€¦, y_N] containing N independent samples from p_LM(⋅∣x_<t) (may contain repeats).

2: \({Y}^{* }:=\,[\,y\in Y:{g}_{1}(\,y,{r}_{t})=\mathop{\max }\limits_{{y}^{{\prime} }\in Y}{g}_{1}(\,{y}^{{\prime} },{r}_{t})]\) (may contain repeats).

3: Sample x_t ~ Unif(Y*)

4: return x_t

Algorithm 2

Sampling a token with multilayer Tournament sampling.

Require: LLM distribution p_LM(⋅∣x_<t), random seed \({r}_{t}\in {\mathcal{R}}\), number of samples N ≥ 2, g function with g-value distribution f_g (see Definition 4), number of layers m ≥ 1.

1: Draw N^m independent samples \({y}_{0}^{0},{y}_{1}^{0},\ldots ,{y}_{{N}^{m}-1}^{0} \sim {p}_{{\rm{LM}}}(\cdot | {x}_{ < t})\) (may contain repeats).

2: for 1 ≤ ℓ ≤ m do

3:  for 0 ≤ j ≤ N^{m−ℓ} − 1 do

4:   \(Y:=\,[\,{y}_{Nj}^{{\ell }-1},{y}_{Nj+1}^{{\ell }-1},\ldots ,{y}_{Nj+N-1}^{{\ell }-1}]\) (may contain repeats).

5:   \({Y}^{* }:=\,[\,y\in Y:{g}_{{\ell }}(\,y,{r}_{t})=\mathop{\max }\limits_{{y}^{{\prime} }\in Y}{g}_{{\ell }}(\,{y}^{{\prime} },{r}_{t})]\) (may contain repeats).

6:   Sample \({y}_{j}^{{\ell }} \sim \,{\rm{Unif}}\,({Y}^{* })\).

7:  end for

8: end for

9: return \({x}_{t}:={y}_{0}^{m}\)

Repeated context masking

To generate a full response, we could simply apply Algorithm 2 on every decoding step, using the sliding-window random seed generator (‘Random seed generator’ section) to generate the random seed r_t for each step. However, it is possible that the same window of context, and thus the same random seed might occur more than once (particularly if the sliding-window size H is small or the response is long). It has been shown that in this scenario, the watermark can introduce a repeated bias that affects the quality of the text, for example, causing repeating loops^24,25. One way to avoid this problem is to apply repeated context masking²⁷, which prevents the watermark from being applied on step t if the context window (x_t−H, …, x_t−1) has been used to watermark previously.

We present the method in Algorithm 3, which we call K-sequence repeated context masking. The integer parameter K ≥ 1 controls for how long context windows are held in the history. In the simplest case of K = 1, we only hold the context history for the duration of generating a single response. For larger integers K > 1, we check against a history of contexts used in the last K responses. In the extreme case, we could set K = ∞ and retain the context history indefinitely. In Supplementary Information section G.2, we show that applying K-sequence repeated context masking achieves K-sequence non-distortion, an important property for quality preservation. In Supplementary Information section G.3, we discuss the trade-offs of smaller and larger K. For most of our experiments we use K = 1.

Algorithm 3

Generating watermarked responses with sliding-window random seed generation and K-sequence repeated context masking.

Require: LLM p_LM(⋅∣⋅), context window size H, pseudorandom hash function h, watermarking key \(k\in {\mathcal{R}}\), sampling algorithm \({\mathcal{S}}:\Delta V\times {\mathcal{R}}\to V\), integer K ≥ 1, stream of prompts (x¹, x², â€¦).

1: for i ≥ 1 do

2:  \({C}_{i}:=\varnothing \)

3:  t ≔ n where n is the length of \({{\bf{x}}}^{i}={{\bf{x}}}_{1}^{i},\ldots ,{{\bf{x}}}_{n}^{i}\)

4:  while \({{\bf{x}}}_{t}^{i}\ne {\mathtt{EOS}}\) do

5:   t ≔ t + 1

6:   if \(({{\bf{x}}}_{t-H}^{i},\ldots ,{{\bf{x}}}_{t-1}^{i})\in {C}_{i}\cup {C}_{i-1}\cup \cdots \cup {C}_{i-K+1}\) then

7:    Sample \({{\bf{x}}}_{t}^{i} \sim {p}_{{\rm{LM}}}(\cdot | {{\bf{x}}}_{ < t}^{i})\)

8:   else

9:    \({r}_{t}:=h({{\bf{x}}}_{t-H}^{i},\ldots ,{{\bf{x}}}_{t-1}^{i},k)\)

10:    Sample \({{\bf{x}}}_{t}^{i}:={\mathcal{S}}({p}_{{\rm{LM}}}(\cdot | {{\bf{x}}}_{ < t}^{i}),{r}_{t})\)

11:    \({C}_{i}:={C}_{i}\cup \{({{\bf{x}}}_{t-H}^{i},\ldots ,{{\bf{x}}}_{t-1}^{i})\}\)

12:   end if

13:  end while

14:  return Response \({{\bf{y}}}^{i}:={{\bf{x}}}_{n+1:t}^{i}\)

15: end for

Scoring functions

A scoring function takes a piece of text x₁, …, x_T along with the random seeds r₁, …, r_T and computes a score, which can then be compared with a threshold to classify the text as watermarked or unwatermarked. Here the random seeds r_t = f_r(x_<t, k) are from the random seed generator (‘Random seed generator’ section). It is noted that a scoring function only requires access to the tokenized text, the watermarking key k and the random seed generator f_r; no access to the LLM is required.

For SynthID-Text, we propose several scoring functions, which are in Supplementary Information section A. All the scores are computed from the g-values of the text. The simplest of these is the mean score, which is simply the mean of the g-values across all timesteps and layers. We also propose a weighted mean score, which re-weights the evidence of each tournament layer. We propose frequentist versions of these scores, which perform a hypothesis test on these means to produce a P value. Lastly, we propose a parameterized Bayesian scoring function, which achieves better performance by learning from data (watermarked and unwatermarked texts) to compute the posterior probability that a text is watermarked.

Experimental details

LLMs and LLM configurations

In our experiments, we use the IT variants of the Gemma 2B and 7B models²⁸. We also use the v0.2 Mistral 7B-IT model²⁹. To generate text, we use top-k sampling³⁶. Following default settings, we use k = 100 for the IT models. We experiment with temperatures of 0.5, 0.7 and 1.0, as varying the temperature changes the entropy of the model, which affects watermark detectability.

Data

To prompt our models we use the ELI5³⁰ dataset, which consists of English questions that require explanatory multi-sentence answers. This simulates a more task-oriented setting. For experiments with non-distortionary watermarking, our ELI5 test set and the development set each contain sets of 10,000 disjoint prompts that are used to prompt the model to obtain watermarked responses. For experiments with distortionary watermarking, we use 1,500 prompts from ELI5 for the test set to prompt the watermarked model. For the unwatermarked samples used as negatives, we use two disjoint sets of human-written responses to 10,000 questions from the ELI5 for the development and test sets.

Text lengths

For some experiments, we evaluate texts of fixed length—for example, 200 tokens. To obtain text of length exactly 200 tokens, we select the subset of texts that are longer than 200 tokens and then truncate them to have exactly 200 tokens.

Detectability metric

To report detectability, we use the true-positive rate (TPR) for a fixed false-positive rate (FPR) of x%, measured empirically. We denote this metric as TPR @ FPR = x%. For example to compute TPR @ FPR = 1%, we take the scores (under some scoring function) of the unwatermarked texts and compute a threshold corresponding to the top-1% highest scores. Then we compute the true-positive rate by measuring the fraction of watermarked texts that score above this threshold. Although some scoring functions allow a precise theoretical guarantee on the false-positive rate—for example, the frequentist scoring functions (Supplementary Information section A.3) which provide a P value—in this work we take the empirical approach described above.

Random seed generator settings

For all watermarking experiments (including Tournament, Gumbel and Soft Red List sampling algorithms), we use the same sliding-window-based random seed generator described in the ‘Random seed generator’ section, with context window size H = 4. We apply one-sequence repeated context masking (‘Repeated context masking’ section).

SynthID-Text settings

Unless otherwise mentioned, for all SynthID-Text experiments, we use m = 30 tournament layers, a Bernoulli(0.5) g-value distribution f_g (Algorithm 2) and the Bayesian scoring function (Supplementary Information section A.4).