Recurrent evolution and selection shape structural diversity at the amylase locus

Amylase gene naming conventions

The reference genome GRC38 represents an H3 haplotype with three copies of the AMY1 gene and one copy each of the AMY2A and AMY2B genes. The three AMY1 copies are identified with labels AMY1A, AMY1B and AMY1C due to the HUGO naming convention requirements for all gene copies to have unique names. However, these various copies of AMY1 genes across different haplotypes are recent duplications that share high sequence similarity, and therefore are referred to simply as AMY1 genes in this paper and others^2,3,15. By contrast, AMY2A and AMY2B stem from a much older gene duplication event and are much more diverged than the different copies of AMY1 genes¹³. They share the AMY2 prefix simply because they are both expressed in the pancreas.

Datasets

Short-read sequencing data were compiled from high-coverage resequencing of the 1,000 Genomes Project (1KG) samples¹⁹, the Simons Genome Diversity Panel (SGDP)²⁰, and the Human Genome Diversity Panel (HGDP)¹⁸. Genomes from GTEx²¹ samples were also assessed, but only for gene expression analyses as the ancestry of these samples was not available. In total, we obtained copy number genotype estimates for 5,130 contemporary samples. Among these, 838 are GTEx samples, 698 are trios from the 1KG, and the rest (n = 3,594, that is, 7,188 haplotypes) are unrelated individual samples compiled from the 1KG, HGDP and SGDP. GTEx and 1KG trio samples were excluded from analyses characterizing the global diversity of the amylase locus. We performed haplotype deconvolutions on all unrelated samples as well as trio data (n = 4,292 total), but the trios were only used for validation purposes.

Supplementary Fig. 25 shows structural variant calls from the gnomAD project⁴⁶. Phased SNP calls from 1KG and HGDP samples were compiled from Koenig et al.⁴⁷, which includes all of our 1KG and HGDP samples but only some of the SGDP samples (n = 3,395 total). These data were used for the analyses of linkage disequilibrium, nucleotide diversity, principal component analysis (PCA) and selection scans⁴⁷.

Ancient genome short-read fastq samples were compiled from Allentoft et al.³⁰ and Marchi et al.²⁹ and were mapped to the human reference genome GRCh38 with BWA (v0.7.17; ‘bwa mem’)⁴⁸. The modern genomes and the 14 Marchi et al. genomes are of high coverage and quality; however, the Allentoft et al. samples were of varying quality and coverage³⁰. The Allentoft et al. dataset included more than 1,600 ancient genomes including 317 newly sequenced ancient individuals alongside 1,492 previously published genomes. Unfortunately, many published ancient genomes have been filtered to exclude multi-mapped reads leaving large gaps over regions such as the amylase locus. After removing genomes with missing data, 690 samples remained. We carefully analysed these 690 genomes to determine their quality by quantifying the standard deviation of genome-wide copy number (after removing the top and bottom fifth percentiles of copy number to exclude outliers). We chose a standard deviation cut-off of 0.49 based on a visual inspection of the copy number data and selected 519 samples (approximately 75% of 690) with sufficient read depth for copy number genotyping. Ancient samples were assigned to one of eight major ancient populations in West Eurasia based on their genetic ancestry, location and age obtained from their original publications^29,30,49,50 (Fig. 5a, Supplementary Table 8 and Supplementary Fig. 19). These populations include: Eastern hunter-gatherer, Caucasian hunter-gatherer, Western hunter-gatherer, early farmer (samples with primarily Anatolian farmer ancestry), Neolithic farmer (samples with mixed Anatolian farmer and Western hunter-gatherer ancestry), Steppe pastoralist (samples with mixed Eastern hunter-gatherer and Caucasian hunter-gatherer ancestry), Bronze Age (samples with mixed Neolithic farmer and Steppe ancestry), and Iron Age to early modern. Finally, four archaic genomes were assessed including three high-coverage Neanderthal genomes and the high-coverage Denisova genome^27,51,52,53.

Long-read haplotype assemblies were compiled from the HPRC²³. Year 1 genome assembly freeze data were compiled along with year 2 test assemblies. Haplotype assemblies were included in our analyses only if they spanned the amylase SVR. Furthermore, in cases in which both haplotypes of an individual spanned the SVR, we checked to ensure that the diploid copy number of amylase genes matched with the read-depth-based estimate of copy number. We noted that several year 1 assemblies (which were not assembled using ONT ultralong sequencing data) appeared to have been misassembled across the amylase locus, as they were either discontiguous across the SVR or had diploid assembly copy numbers that did not match with short-read-predicted copy number. We thus reassembled these genomes incorporating ONT ultralong sequence using the Verkko assembler (v1.3.1)⁵⁴, constructing improved assemblies for HG00673, HG01106, HG01361, HG01175, HG02148 and HG02257. Alongside these HPRC genome assemblies, we included GRCh38 and the newly sequenced T2T-CHM13 reference²⁴.

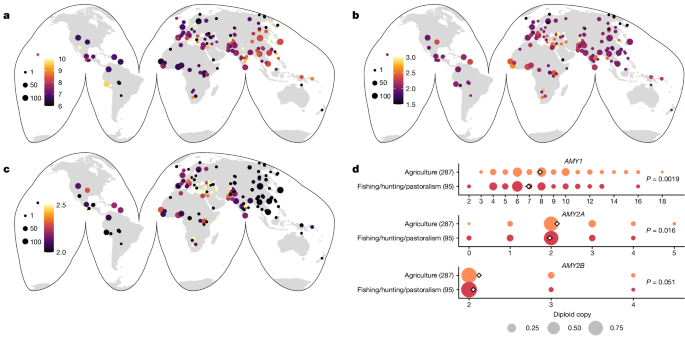
Determination of subsistence by population

The diets of several populations (see Supplementary Table 2) were determined from the literature from the following sources^{2,55,56,57,58,59,60,61,62,63}. We were able to identify the traditional diets for 33 populations. All other populations were excluded from this analysis.

Read-depth-based copy number genotyping

Copy number genotypes were estimated using read depth as described in ref. ¹⁶. In brief, read depth was quantified from BAMs in 1,000-bp sliding windows in 200-bp steps across the genome. These depths were then normalized to a control region in which no evidence of copy number variation was observed in more than 4,000 individuals. Depth-based ‘raw’ estimates of copy number were then calculated by averaging these estimates over regions of interest. Regions used for genotyping are found in Supplementary Table 10. We note that the AMY2Ap pseudogene is a partial duplication of AMY2A that excludes the approximately 4,500 bp of the 5′ end of the gene. This region can thus be used to genotype the AMY2A copy without ‘double counting’ AMY2Ap gene duplicates. Copy number genotype likelihoods were estimated by fitting modified Gaussian mixture model to raw copy estimates across all individuals with the following parameters: k, the number of mixture components, set to be the difference between the highest and lowest integer-value copy numbers observed; π, a k-dimensional vector of mixture weights; σ, a single-variance term for mixture components; and o, an offset term by which the means of all mixture components are shifted. The difference between mixture component means was fixed at 1, and the model was fit using expectation maximization (Supplementary Fig. 1). The copy number maximizing the likelihood function was used as the estimated copy number for each individual in subsequent analyses. Comparing these maximum likelihood copy number estimates with droplet digital PCR yielded very high concordance with r²â€‰= 0.98, 0.99 and 0.96 for AMY1, AMY2A and AMY2B, respectively (Supplementary Fig. 1). For comparisons of copy number as a function of sustenance, populations were downsampled to a maximum of 50 individuals. We also used a linear mixed effects model approach in which all samples were maintained, which provided similar results (P = 0.013, P = 0.058 and P = 0.684 for AMY1, AMY2A and AMY2B, respectively).

Analysis of gene expression

Gene expression data from the GTEx project²¹ were downloaded alongside short-read data (see above section). Normalized gene expression values for AMY2A and AMY2B were compared with copy number estimates using linear regression (Extended Data Fig. 2).

MAP-graph construction

Regions overlapping the amylase locus were extracted from genome assemblies in two different ways. First, we constructed a PanGenome Research Tool Kit (PGR-TK) database from the HPRC year 1 genome assemblies and used the default parameters of w = 80, k = 56, r = 4 and min-span = 64 for building the sequence database index. The GRCh38 chromosome 1: 103655518–103664551 was then used to identify corresponding AMY1/AMY2A/AMY2B regions across these individuals. Additional assemblies were subsequently added to our analysis by using minimap2 (ref. ⁶⁴) to extract the amylase locus from those genome assemblies. The MAP-graph and the principal bundles were generated using revision (v0.4.0; git commit hash: ed55d6a8). The Python scripts and the parameters used for generating the principal bundle decomposition can be found in the associated GitHub repository. The position of genes along haplotypes was determined by mapping gene modes to haplotypes using minimap2 (ref. ⁶⁴).

Analysis of mutations at amylase genes

To identify mutations in amylase genes from long-read assemblies and evaluate their functional impact, we first aligned all amylase gene sequences to AMY1A, AMY2A and AMY2B sequences on GRCh38 using minimap2 (ref. ⁶⁴). We then used paftools.js⁶⁴ for variant calling, and vep-v.105.0 (ref. ⁶⁵) for variant effect prediction.

PGGB-based graph construction

Although the existing pangenome graphs from the HPRC provide a valuable resource, we discovered that they did not provide the best reference system for genotyping copy number variation. Our validation of the genotyping approach revealed that we would experience high genotyping error when gene copies (for example, all copies of AMY1 or all copies of AMY2B) were not fully ‘collapsed’ into a single region in the graph. We thus elected to rebuild the graph locally to improve genotyping accuracy for complex structural variants. This achieves substantially improved results by allowing multiple mappings of each haplotype against others, which leads to a graph in which multi-copy genes are collapsed into single regions of the graph. This collapsed representation is important for graph-based genotyping. In addition, we incorporated additional samples, some of which were reassembled by us, that were not part of the original dataset from the HPRC to have a more comprehensive representation of variability in the amylase locus, which required rebuilding the pangenome graph model at the amylase locus.

A PGGB graph was constructed from 94 haplotypes spanning the amylase locus using PGGB (v0.5.4; commit 736c50d8e32455cc25db19d119141903f2613a63)²⁵ with the following parameters: ‘-n 94’ (the number of haplotypes in the graph to be built) and ‘-c 2’ (the number of mappings for each sequence segment). The latter parameter allowed us to build a graph that correctly represents the high copy number variation in such a locus. We used ODGI (v0.8.3; commit de70fcdacb3fc06fd1d8c8d43c057a47fac0310b)⁶⁶ to produce a Jaccard distance-based (that is, 1 − Jaccard similarity coefficient) dissimilarity matrix of paths in our variation graph (‘odgi similarity -d’). These pre-computed distances were used to construct a tree of relationships between haplotype structures using neighbour joining.

Haplotype deconvolution approach

We implemented a pipeline based on the workflow language Snakemake (v7.32.3) to parallelize haplotype deconvolution (that is, assign to a short-read-sequenced individual the haplotype pair in a pangenome that best represents its genotype at a given locus) in thousands of samples.

Given a region-specific PGGB graph (gfa; see ‘PGGB-based graph construction’), a list of short-read alignments (BAM/CRAM), a reference build (fasta) and a corresponding region of interest (chr: start–end; based on the alignment of the BAM/CRAM), our pipeline ran as follows:

1. 1.

   Extracted the haplotypes from the initial pangenome using ODGI (v0.8.3; ‘odgi paths -f’)⁶⁶.

2. 2.

   For each short-read sample, extracted all the reads spanning the region of interest using SAMTOOLS (v1.18; ‘samtools fasta’)⁶⁷.

3. 3.

   Mapped the extracted reads back to the haplotypes with BWA (v0.7.17; ‘bwa mem’)⁴⁸. To map ancient samples, we used ‘bwa aln’ with parameters suggested in Oliva et al.⁶⁸ instead: ‘bwa aln -l 1024 -n 0.01 -o 2’.

4. 4.

   Computed a node depth matrix for all the haplotypes in the pangenome; every time a certain haplotype in the pangenome loops over a node, the path depth for that haplotype over that node increases by one. This was done using a combination of commands in ODGI (‘odgi chop -c 32’ and ‘odgi paths -H’).

5. 5.

   Computed a node depth vector for each short-read sample; short-read alignments were mapped to the pangenome using GAFPACK (https://github.com/ekg/gafpack; commit ad31875) and their coverage over nodes was computed using GFAINJECT (https://github.com/ekg/gfainject; commit f5feb7b).

6. 6.

   Compared each short-read vector (see step 5) with each possible pair of haplotype vectors (see step 4) by means of cosine similarity using (https://github.com/davidebolo1993/cosigt; commit e247261; which measures the similarity between two vectors as their dot product divided by the product of their lengths). The haplotype pair having the highest similarity with the short-read vector was used to describe the genotype of the sample.

7. 7.

   The final genotypes were assigned as the corresponding consensus structures of the highest similarity pair of haplotypes.

Our pipeline is publicly available on GitHub (https://github.com/raveancic/graph_genotyper) and is archived in Zenodo (https://zenodo.org/doi/10.5281/zenodo.10843493).

We assessed the accuracy of the haplotype deconvolution approach in several different ways. First, we assessed 35 individuals (70 haplotypes) for which both short-read sequencing data and long-read diploid assemblies were available. In 100% of cases (70 of 70 haplotypes), we accurately distinguished the correct haplotypes present in an individual from short-read sequencing data. We further assessed how missing haplotypes in the pangenome graph might assess the accuracy of our approach by performing a ‘leave-one-out, jackknifing’ analysis. In this approach, for each of the 35 long-read individuals, we rebuilt the variation graph with a single haplotype excluded and tested our ability to identify the correct consensus haplotype from the remaining haplotypes. The true positive rate was approximately 93% in this case. Second, we compared our haplotype deconvolutions to haplotypes determined by inheritance patterns in 44 families in a previous study¹⁵ (Supplementary Table 3). We note that this study hypothesized the existence of an H4A4B4 haplotype without having observed it directly. In our study, we also found no direct evidence of the H4A4B4 haplotype. Furthermore, we found that inheritance patterns are equally well explained by other directly observed haplotypes and thus exclude these predictions from our comparisons (two individuals excluded). We identified the exact same pair of haplotypes in 95% of individuals (125 of 131 individuals), and in 97% of individuals (288 of 298 individuals), the haplotype pair that we identified is among the potential consistent haplotype pairs identified from inheritance. Third, we compared inheritance patterns in 602 diverse short-read-sequenced trios from the 1KG populations¹⁹. For each family, we randomly selected one parent and assessed whether either of the two offspring haplotypes were present in this randomly selected parent. Across all families, this proportion, p, represents an estimate of the proportion of genotype calls that are accurate in both the offspring and that parent, thus the single sample accuracy can be estimated as the square root of p. From these analyses, we identified 533 of 602 parent–offspring genotype calls that are correct, corresponding to an estimated accuracy of 94%. Fourth, we compared our previously estimated reference genome read-depth-based copy number genotypes to those predicted from haplotype deconvolutions across 4,292 diverse individuals. These genotypes exhibited 95–99% concordance across different amylase genes (95%, 97% and 99% for AMY1, AMY2A and AMY2B, respectively). Cases in which the two estimates differed were generally high-copy genotypes for which representative haplotype assemblies have not yet been observed and integrated into the graph (Extended Data Fig. 7a). Overall we thus estimated the haplotype deconvolution approach to be approximately 95% accurate for modern samples, and thus choose not to propagate the remaining 5% uncertainty into downstream analyses.

To determine the impact of coverage and technical artefacts common in ancient DNA, we performed simulations. We selected 40 individuals having both haplotypes represented in the AMY graph and, for those, we simulated short reads mirroring error profiles in modern and ancient genomes across different coverage levels. More specifically, we simulated paired-end short reads for the modern samples with wgsim (https://github.com/lh3/wgsim; commit a12da33, ‘wgsim −1 150 −2 150’) and single-end short reads for the ancient samples with NGSNGS⁶⁹ (commit 559d552, ‘ngsngs -ne -lf Size_dist_sampling.txt -seq SE -m b7,0.024,0.36,0.68,0.0097 -q1 AccFreqL150R1.txt’ following the suggestions by the author in https://github.com/RAHenriksen/NGSNGS). Synthetic reads were then aligned against the GRCh38 build of the human reference genome using bwa-mem2 (ref. ⁷⁰; commit 7f3a4db). For samples modelling modern individuals, we generated 5–30X coverage data, whereas for those modelling ancient genomes, we aimed for lower coverage (1–10X) to better approximate true-to-life data. We ran our haplotype deconvolution pipeline independently for modern and ancient simulated samples, as well as varying coverage levels. Out of 480 tests, only 9 (approximately 1%) yielded incorrect predictions, exclusively in ancient simulated sequences, with coverage ranging from 1X to 4X. Cosine similarity scores for ancient simulated sequences ranged from 0.789 to 0.977 (median of 0.950), whereas scores for modern simulated sequences ranged from 0.917 to 0.992 (median of 0.981; Extended Data Fig. 7b). We therefore conclude that the haplotype deconvolution method is also highly accurate for ancient samples. Out of an abundance of caution, we further imposed a conservative quality score threshold of 0.75 to ancient samples, resulting in 288 ancient samples with high-confidence haplotype assignment out of a total of 533 (Supplementary Figs. 20 and 21). We note that the haplotype deconvolutions in ancient samples are probably more accurate than read-depth genotypes, which tend to be biased towards higher copy number.

Linkage disequilibrium estimation

To investigate pairwise linkage disequilibrium across the SVR region at a global scale, we first merged our copy number estimates with the joint SNP call set from the HGDP and 1KG⁴⁷, resulting in a variant call set of 3,395 diverse individuals with both diploid copy number genotypes and phased SNP calls. In brief, we used bcftools (v1.9)⁶⁷ to filter HGDP and 1KG variant data for designated genomic regions on chromosome 1, including the amylase SVR and flanking regions defined as bundle 0 and bundle 1 (distal and proximal, respectively) using the GRCh38 reference coordinate system (–region chromosome 1: 103,456,163–103,863,980 in GRCh38). The resulting output was saved in variant call format (vcf), keeping only biallelic SNPs (-m2 -M2 -v snps), and additionally filtered with vcftools (v.0.1.16)⁷¹ with -keep and -recode options for lists of individuals grouped by continental region in which we were able to estimate diploid copy numbers. Population-specific vcf files were further filtered for a minor allele frequency filter threshold of 5% (–minmaf 0.05) and used to generate a numeric genotype matrix with the physical positions of SNPs for linkage disequilibrium calculation (R² statistic) and plotting with the LDheatmap⁷² function in R (v4.2.2).

To further dissect the unique evolutionary history of the amylase locus, we compared regions with high R² across the SVR with linkage disequilibrium estimates for pairs of SNPs across regions of similar size in chromosome 1. We specifically focused on pairs of SNPs spanning bundle 0 (chromosome 1: 103456163–103561526 in GRCh38) and the first 66-kb of bundle 1, hereafter labelled as bundle 1a (chromosome 1: 103760698–103826698 in GRCh38), as revealed by the linkage disequilibrium heatmap. Then, we computed the R² values for any pair of SNPs in chromosome 1 for each superpopulation within a minimum of 190-kb distance (that is, the equivalent distance from the bundle 0 end to the bundle 1a start using the GRCh38 reference coordinate system) and maximum 370-kb distance (that is, the equivalent distance from the bundle 0 start to the bundle 1a end using the GRCh38 reference coordinate system). To calculate pairwise linkage disequilibrium across the human chromosome 1 for different populations, we ran plink (v1.90b6.21)⁷³ with options -r2 –ld-window 999999 –ld-window-kb 1000 –ld-window-r2 0 –make-bed –maf 0.05, using population-specific vcf files for a set of biallelic SNPs of 3,395 individuals from the HGDP and 1KG as input. As the resulting plink outputs only provide R² estimates for each pair of SNPs and respective SNP positions, we additionally calculated the physical distances between pairs of SNPs as the absolute difference between the base-pair position of the second (BP_B) and first (BP_A) SNP. We then filtered out distances smaller than 190 kb and greater than 370 kb, and annotated the genomic region for each R² value based on whether both SNPs fall across the SVR or elsewhere in chromosome 1. The distance between SNP pairs was also binned into intervals of 20,000 bp, and the midpoint of each interval was used for assessing linkage disequilibrium decay over genomic distances. The resulting dataset was imported in R to compute summary statistics comparing linkage disequilibrium across each major continental region, or superpopulations, and we used ggplot2 to visualize the results.

Coalescent tree, ancestral-state reconstruction and PCA

To construct the coalescent tree, we first extracted bundle 0 and bundle 1a sequences from all 94 haplotypes (that is, distal and proximal unique regions flanking the amylase SVR) that went through principal bundle decomposition. On the basis of their coordinates on the human reference genome (GRCh38), we used SAMtools (v1.17)⁷⁴ to extract these sequences from three Neanderthal and one Denisovan genomes that are aligned to GRCh38. We used kalign (v3.3.5)⁷⁵ to perform multiple sequence alignment on bundle 0 and bundle 1a sequences. We used IQ-TREE (v2.2.2.3)⁷⁶ to construct a maximum likelihood tree with Neanderthal and Denisova sequences as the outgroup, using an estimated 650 kyr human–Neanderthal split time for time calibration²⁷. We used ggtree (v3.6.2)⁷⁷ in R (v4.2.1) to visualize the tree and annotated each tip with its structural haplotype and amylase gene copy numbers. We used cafe (v5.0.0)⁷⁸ to infer the ancestral copy numbers of each of the three amylase genes along the time-calibrated coalescent tree (excluding the outgroups) and to estimate their duplication/deletion rates. The timing of each duplication/deletion event was estimated based on the beginning and end of the branch along which the amylase gene copy number had changed. We used ggtree and ggplot (v3.4.2) in R to visualize these results, and used Adobe Illustrator (v27.5) to create illustrations for several of the most notable duplication/deletion events⁷⁹.

Next, we performed a PCA combining 94 HPRC haplotype sequences with variant calls for 3,395 individuals from the HGDP and 1KG. We first aligned all 94 bundle 0 and 94 bundle 1a haplotype sequences to the human reference genome (GRCh38) using minimap2 (v2.26)⁶⁴, and called SNPs from haplotypes using paftools.js. Each haplotype sequence appears as a pseudo-diploid in the resulting vcf file (that is, when the genotype is different from the reference, it is coded as being homozygous for the non-reference allele). These haplotype-specific vcf files were merged together and filtered for biallelic SNPs (-m2 -M2 -v snps) with bcftools, resulting in a pseudo-diploid vcf file from 94 haplotype sequences for each bundle. These were then merged with the respective bundle 0 and bundle 1a vcf files from the HGDP and 1KG, also filtered for biallelic SNPs, using bcftools. Finally, we ran plink with a minor allele frequency of 5% (–maf 0.05) to obtain eigenvalues and eigenvectors for PCA and used ggplot (v3.4.2) to visualize the results. These analyses were conducted with bundle 0 and bundle 1a separately, with highly concordant results (Supplementary Figs. 3 and 4). Analyses focused on bundle 0 are mostly reported in the main text (Fig. 3 and Extended Data Fig. 6), whereas bundle 1a results are shown as extended data (Extended Data Fig. 4).

Signatures of recent positive selection in modern human populations

To investigate very recent or ongoing positive selection at the amylase locus in modern humans, we first looked for significant signatures of reduced genetic diversity across the non-duplicated regions adjacent to the SVR compared with chromosome 1 in different populations worldwide. This stems from the assumption that, given low SNP density across the SVR, the high levels of linkage disequilibrium found between pairs of SNPs spanning bundle 0 and bundle 1a indicate that SNPs in bundle 0 or bundle 1 can be used as proxies for the selective history of the linked complex structures of the SVR. We calculated nucleotide diversity (π) on sliding windows of 20,000 bp spanning GRCh38 chromosome 1 with vcftools using population-specific vcf files from the HGDP and 1KG filtered for a set of biallelic SNPs as input. Each window was annotated for the genomic region, namely, bundle 0, SVR and bundle 1a. All windows comprising the SVR were removed from the resulting output due to low SNP density. We then used ggplot2 in R to compare and visualize nucleotide diversity in the flanking regions of the amylase locus (that is, bundle 0 and bundle 1a) and the rest of chromosome 1 for each major continental region or super-population.

To identify either soft-selective and hard-selective sweeps at the flanking regions of the SVR, we computed several different extended haplotype homozygosity-based statistics and statistics based on distortions of the haplotype frequency spectrum (Supplementary Table 5). Vcf files from the HGDP and 1KG chromosomes 1–22 GRCh38 were filtered for biallelic SNPs and minor allele frequency of 0.05 for target populations with over 10 individuals to calculate iHS⁸⁰, nSL⁸¹ and XP-nSL⁸² as implemented in selscan (v2.0.2)⁸³ (see Supplementary Table 5 for a description of populations and selection statistics). Utah residents with Northern and Western European ancestry (CEU) and Yoruba (YRI) populations were also included to confirm the ability of the tests to consistently identify the LCT hard sweep in CEU and in relation to the amylase locus (Supplementary Table 5). Scores for these statistics were normalized using the genome-wide empirical background with selscan’s co-package norm (v1.3.0). This was also used to compute the fraction of the standardized absolute values > 2 for each statistic in non-overlapping 100-kb windows genome-wide⁸⁰. For XP-nSL statistics, modern rainforest hunter-gatherers in Africa and the pastoralists Yakut were used as reference populations, so that positive scores correspond to possible sweeps in the populations with traditionally agricultural diets. We also used lassip (v1.2.0)⁸⁴ to compute H12 and H2/H1 statistics⁸⁵ and saltiLASSI Λ⁸⁴ on sliding windows of 201 SNPs with intervals of 100 SNPs. SNP positions within the SVR were removed from the resulting outputs due to low SNP density. We then compared the average and distribution of all selection statistics across individual SNPs or windows located within bundle 0 and bundle 1a (labelled as ‘AMY region’) and located within chromosome 2: 135–138 Mb (labelled as the ‘LCT region’) with that of the rest of the genome using geom_stats() and geom_density() functions in ggplot2 (Supplementary Table 5 and Supplementary Figs. 6–18). We also used an outlier approach and focused on the top 0.05% of the test statistic across all windows genome-wide for modern populations of known subsistence, and considered estimates above this threshold to be strong signals of selection⁸⁰. To improve detection power, we computed Fisher’s exact score⁸⁶ from SNP ranks for the two selection statistics that were better able to identify signatures of selection at the AMY locus. Then, we investigated whether the scores computed from these statistics for SNPs located at the AMY locus were among the top 1% of Fisher’s exact scores estimated genome-wide (Supplementary Table 5 and Supplementary Fig. 18).

Inference of recent positive selection in West Eurasian populations using ancient genomes

To determine whether changes in the frequency of different structural haplotypes over the past 12,000 years were consistent with positive selection, we first grouped amylase structural haplotypes (n = 11) into those with the ancestral number of amylase gene copies (three total) or with amylase gene duplications (five or more copies). We used three complementary approaches to infer the selection coefficient associated with duplication-containing haplotypes. First, we used ApproxWF³¹ to perform Bayesian inference of the selection coefficient from binned allele frequency trajectories. We ran ApproxWF for 101,0000 Markov chain Monte Carlo (MCMC) steps with parameters n = 10,000, h = 0.5 and pi = 1. We assumed a generation time of 30 years to convert the age of ancient samples from years to generations. The first 10,000 steps of the MCMC process were discarded in all analyses. Next, we used bmws (v0.1.0)³² to estimate the allele frequency trajectory and time-varying selection from genotype data with parameters -d diploid -l 4.5 -g 30 -n 10000 -t. We further ran 1,000 bootstrap replicates to obtain 95% credible intervals around our estimates. Last, we used an approximate Bayesian computation approach adapted and modified from ref. ³³ to explicitly account for the demographic processes underlying the allele frequency changes. We performed extensive forward-in-time simulations using SLiM (v3.7.1)⁸⁷ based on a well-established demographic model for West Eurasians³⁸ that includes major population split and admixture events as well as population growth (Supplementary Table 11). We allowed three model parameters to vary across simulations: selection coefficient (s), the time of selection onset (t, in kyr bp) and the initial allele frequency in the ancestral population (f). Selection is only applied to known agricultural populations (that is, early farmers, Neolithic farmers, and Bronze Age to present-day Europeans), and its strength is assumed to be constant over time. These parameter values were set in evenly spaced intervals (that is, 21 values of s ∈ [−0.01, 0.04], 21 values of t ∈ [3, 15], 31 values of f ∈ [0.05, 0.8]), and 1,000 replicate simulations were run for each unique parameter combination. This resulted in 13,671,000 simulations in total. For each simulation, we calculated the difference between the observed and the expected binned allele frequency trajectories, accounting for uneven sampling in time and genetic ancestry. We then selected the top 0.1% of simulations (that is, 13,671 simulations) that best resemble the observed data to approximate the posterior distribution of model parameters. We also examined the allele frequency changes (that is, the difference between allele frequencies in the first and last time bin) across all neutral simulations with s = 0 and compared them with the observed allele frequency change in the data (Supplementary Fig. 25).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.