Observations and data analysis
X-ray data
Chandra
We downloaded processed Chandra images and event files and associated calibration data from the Chandra archive. We carried out analysis using CIAO version 4.16 (ref.â36) and CALDB version 4.11.0. We checked for pileup using the pileup_map task, finding a pileup fraction of about 1% only for the central 4âpixels of the middle exposure. Therefore, pileup has negligible impact on our analysis. Count rates were extracted using the srcflux task. We used a 2-arcsec (4-pixel) circular radius and the default point-spread function (PSF) model. The background was estimated using an annular region with inner and outer radii of 15 and 60âarcsec, respectively, centred on AT2019qiz. This excludes other point sources, including the SE source (see below). The CIAO srcflux task includes the Bayesian GregoryâLoredo algorithm37 to determine the optimal number of bins for investigating a time-varying (or, more formally, periodic) signal. The algorithm provides an odds ratio for variability (2.5 for AT2019qiz) and a light curve with the number of bins that maximizes this odds ratio. None of the other five sources in Extended Data Fig. 1 show an odds ratio >1.
We extract the spectrum in both eruption and quiescence (see below) using the specextract task. The spectrum of the eruption is soft and can be reasonably fit with a blackbody of about 100âeV. We perform a more detailed spectral analysis of AT2019qiz using the later eruptions and quiescent-phase data from instruments with greater sensitivity to softer (0.3â0.7âkeV) X-rays (see sections âSwift/XRT and the quiescent spectrum of AT2019qizâ and âNICERâ).
The nature of the SE X-ray source
The Chandra images show a nearby source approximately 7âarcsec to the SE (labelled âSE sourceâ in Fig. 1). It overlaps with the PSF of AT2019qiz in all instruments other than Chandra. We extracted individual X-ray (0.5â7.0-keV) spectra from all three Chandra obsIDs to characterize the SE source. We perform spectral analysis with the Bayesian X-ray Analysis (BXA) software version 4.0.7 (ref.â38), which connects the nested sampling algorithm UltraNest39 with the fitting environment XSPEC version 12.13.0c (ref.â40), in its Python version PyXspec. To improve the quality of the spectrum, we jointly fit all three Chandra obsIDs. The source can be fit with a simple power-law model with foreground absorption (tbabsâÃâcflux(pow)) and is consistent with being constant over all three obsIDs. The neutral column density was fixed at the Milky Way value of 6.6âÃâ1020âcmâ2. The 0.5â3.0-keV flux in the model is \({2.1}_{-0.9}^{+1.6}\times 1{0}^{-14}\,{\rm{erg}}\,{{\rm{s}}}^{-1}\,{{\rm{cm}}}^{-2}\) (90% posterior) and the photon index of the power law is Îâ=â1.8â±â0.5 (90% posterior). The fit is shown in Extended Data Fig. 4a.
Swift/XRT and the quiescent spectrum of AT2019qiz
We obtained Target of Opportunity time to follow up AT2019qiz with Swift/XRT. Eleven observations were obtained from 12 March 2024 to 14 March 2024, with a typical exposure time of about 1,200âs per visit and cadence of 4.5âh. We clearly detect one eruption in the new data (Fig. 1). We also reanalysed all previous XRT data for this source obtained under previous programmes, using the online tools available through the UK Swift Science Data Centre41,42.
Owing to the better sensitivity at soft energies compared with Chandra, we are able to model the underlying disk spectrum using the XRT observations during the quiescent phase. For this, we use a colour-corrected thermal disk model (tdediscspec)43, to be consistent with the full spectral energy distribution (SED) fit (see section âDisk modellingâ). Given the larger PSF of XRT, we simultaneously model the AT2019qiz and the SE source contributions to the total spectrum. We use the model tbabs Ãâ(zashift(tdediscspec)â+âcflux(pow)), in which zashift(tdediscspec) is the contribution from AT2019qiz and cflux(pow) is the contribution from the SE source. The fit does not require a redshifted absorption component. We use PyXspec and BXA. For the disk parameters (that is, AT2019qiz), we assume flat priors; however, for the SE source, we use the posteriors from fitting its spatially resolved Chandra spectrum (see section âThe nature of the SE X-ray sourceâ) as the priors. Extended Data Fig. 4b shows their individual contributions to the observed spectrum, confirming that AT2019qiz dominates at energies below ââ1.0âkeV. The posteriors of the fit indicate a peak disk temperature kTpâ=â67â±â10âeV (90% posterior), in agreement with the bulk TDE population44.
Archival data from Swift/XRT
The X-ray spectrum of AT2019qiz observed by Swift/XRT in 2019â2020 was reported to be hard16,21, suggesting a possible contribution from the SE source. To test this, we fit the combined spectrum (MJDâ58714 to 59000) with the same power law plus disk model. We again use our power-law-fit posteriors for the SE source from Chandra as a prior in BXA and this time fix the temperature of the disk component while letting its flux vary freely. The early-time XRT spectrum is entirely consistent with the SE source, with no statistically significant contribution from the disk component (Extended Data Fig. 4c). This results in a 3Ï upper limit on the flux (0.3â1.0âkeV) from AT2019qiz at early times of â¤1.4 Ãâ10â14âergâsâ1âcmâ2, or a luminosity â¤7.2âÃâ1039âergâsâ1.
By contrast, AT2019qiz is brighter and detected at high significance in data from 2022 onwards, with a spectrum dominated by the thermal component21. The luminosity of AT2019qiz measured during all quiescent phases with XRT and Chandra is roughly 1041âergâsâ1, more than an order of magnitude fainter than the eruptions. Extended Data Fig. 6 shows the observation from 2022 in bins of 5âks. The final bin shows an increase in flux, but the temporal baseline is too short to confirm or rule out that this represents the onset of a QPE (see also Fig. 4). The spectral fit from ref.â21 is consistent with a blackbody with kTBBâ=â130â±â10âeV, dominated by the final bin. We use the blackbody spectrum to calculate the luminosity in the final bin and exclude this bin from the disk model fit in Fig. 4a. We stack the remaining counts in a single bin and compute the quiescent luminosity using the fit from Extended Data Fig. 4.
NICER
NICER45,46 observed AT2019qiz in two distinct campaigns, first at early times (around optical peak) from 25 September 2019 to 5 November 2019 and another at late times (about 1,600âdays after optical peak) from 29 February 2024 to 9 March 2024.
The cleaned events lists were extracted using the standard NICER Data Analysis Software (HEASoft 6.33.2) tasks nicerl2 using the following filters: nicersaafilt=YES, saafilt=NO, trackfilt=YES, ang_dist=0.015, st_valid=YES, cor_range=â*-*â, min_fpm=38, underonly_range=0-80, overonly_range=â0.0-1.0â, overonly_expr=â1.52*COR SAX**(-0.633)â, elv=30 and br_earth=40. The whole dataset was acquired during orbit night-time and hence the daytime optical light leak (https://heasarc.gsfc.nasa.gov/docs/nicer/data_analysis/nicer_analysis_tips.html#lightleakincrease) does not apply to our data analysis. The latest NICER calibration release xti20240206 (6 February 2024) was used. Light curves in the 0.3â1.0-keV range were extracted using the nicerl3-lc task with a time bin size of 100âs and the SCORPEON background model.
The data obtained in the first campaign show no evidence for QPEs. Although the cadence is lower than that of the late-time data, it should be sufficient to detect QPEs occurring with the same frequency and duration as at late times, with a probability of detecting no QPEs of about 0.02 (using binomial statistics with a 20% duty cycle). We can therefore probably rule out QPEs within the first approximately two months after TDE fallback started (estimated to have occurred around 11 September 2019 (ref.â16)). However, we note that we would not expect QPEs during this phase in any model, as AT2019qiz was found to have an extended debris atmosphere16, which remained optically thick to X-rays until much later21.
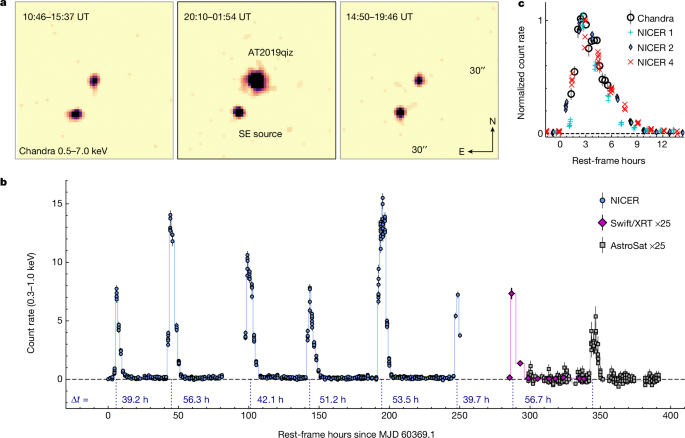
During the second observing campaign, we clearly detect QPEs. The field of view of NICER is shown in Extended Data Fig. 1, overlaid on the Chandra image. All of the sources detected by Chandra have intensities (at energies lower than 1âkeV) more than a factor of 10 below the measured peak of the QPE. Any contributions from these sources to the NICER spectra are further diminished by their offset angles from the centre of the field. We conclude that the NICER counts during eruptions are completely dominated by AT2019qiz. The six consecutive eruptions detected by NICER were modelled using a skewed Gaussian fit to each peak (Extended Data Fig. 2). We measure rest-frame delay times of 39.3â±â0.3, 56.3â±â0.3, 42.1â±â0.3, 51.2â±â0.2 and 53.5â±â0.2âh between successive eruptions.
Given the high count rate and good coverage, we extracted time-resolved X-ray spectra from the second NICER eruption (Fig. 1) in the 0.3â0.9-keV band. We created Good Time Intervals (GTIs) with nimaketime for four intervals representing the rise, peak and decay (two phases) of the eruption. We extracted these spectra using the nicerl3-spec task and produced SCORPEON background spectra in âfile modeâ (bkgmodeltype=scorpeon bkgformat=file) for each of the four GTIs. We simultaneously fit the four spectra using PyXspec and BXA, assuming the model tbabsâÃâzashift(bbody). We fixed the redshift to zâ=â0.0151 and included foreground absorption, with a neutral hydrogen column density fixed to nHâ=â6.6âÃâ1020âcmâ2 (ref.â47). We initially included a redshifted absorber, but the model preferred zero contribution from this component, so we excluded it for simplicity. The full posteriors of the parameters are shown in Extended Data Fig. 3.
AstroSat/SXT
We observed AT2019qiz with AstroSat48 for four days starting on 12 March 2024âUT using the Soft X-ray Telescope (SXT)49 and the Ultra-Violet Imaging Telescope (UVIT)50,51. We used the level2 SXT data processed at the Payload Operation Centres using sxtpipeline v1.5. We merged the orbit-wise level2 data using SXTMerger.jl. We extracted the source in 200-s bins using a circular region of 12âarcmin. The broad PSF of the SXT does not leave any source-free regions for simultaneous background measurement. However, the background is low (0.025â±â0.002âcountsâsâ1) and steady. As the quiescent flux measured by Chandra is below the SXT detection limit, we take this count rate as our background estimate and subtract it from the light curve. SXT detected one eruption (MJDâ60383.548).
Optical/UV observations
HST
We observed AT2019qiz using HST on 21 December 2023âUT (MJDâ60299.55), obtaining one orbit with the Wide-Field Camera 3 (WFC3) UVIS channel in the F225W band. We downloaded the reduced, drizzled and charge-transfer-corrected image from the HST archive. We clearly detect a UV source coincident with the nucleus of the host galaxy. We verify that this source is consistent with a point source both by comparing the profile with other point sources in the image using the RadialProfile task in photutils and by confirming that the fraction of counts within apertures of 3 and 10âpixels are consistent with published encircled energy fractions in the UVIS documentation.
We perform aperture photometry using a 10-pixel (0.396-arcsec) circular aperture, measuring the galaxy background per square arcsecond using a circular annulus between 20 and 40âpixels and subtracting this from the source photometry. Although we cannot measure the galaxy light at the precise position of AT2019qiz, having no UV images free from TDE light, the estimated background within our aperture is <2% of the transient flux, so our results are not sensitive to this approximation. We correct to an infinite aperture using the encircled energy fraction of 85.8% recommended for F225W. The zero point is derived from the image header, including a chip-dependent flux correction. We measure a final magnitude of 20.63â±â0.03â(AB).
Although the angular scale of about 25âpc is not small enough to rule out a nuclear star cluster (NSC), the UV source is an order of magnitude brighter than known NSCs52. Moreover, NSCs are generally red53 and many magnitudes fainter than their host galaxies in bluer bands. The magnitude of the source we detect is comparable with the total UV magnitude of the galaxy16. An unresolved nuclear source was also detected in the QPE source GSNâ069 (ref.â54).
Ground-based photometry
Numerous observations of this galaxy have been obtained by all-sky optical surveys both before and after the TDE. The optical emission was independently detected by ZTF55,56, the Asteroid Terrestrial-impact Last Alert System (ATLAS)57, Pan-STARRS58 and the Gaia satellite59.
Pan-STARRS reaches a typical limiting magnitude of about 22 in the broad w filter (effective wavelength of 6,286âà ) in each 45-s exposure. All observations are processed and photometrically calibrated with the PS image-processing pipeline60,61,62. We downloaded and manually vetted all w-band observations of AT2019qiz since September 2019 and, in most cases, confirm a clean subtraction of the host galaxy light. We also retrieved ZTF forced photometry63 in the r band (with a similar effective wavelength of 6,417âà ). Owing to the shallower limiting magnitude of about 20.5, we stack the fluxes in 7-day bins. Both surveys clearly detect a continuing plateau, persisting for >1,000âdays with a luminosity νLν ââ7âÃâ1040âergâsâ1. All Pan-STARRS and ZTF photometry was measured after subtraction of pre-TDE reference images using dedicated pipelines and hence include only light from AT2019qiz.
Although the optical light curves show scatter consistent with noise, they do not seem to exhibit the intense flaring behaviour seen in the X-rays. An order-of-magnitude flare in the optical would easily be detected even in the unbinned ZTF photometry. Assuming a duty cycle of 20%, and conservatively restricting to data since January 2022 (when we first see signs of day-timescale X-ray variability with XRT), the probability of never detecting an eruption simply because of gaps in cadence is â²10â13.
To test for optical variability on shorter timescales, we conducted targeted observations with the 1.8-m Pan-STARRS2 telescope in Hawaii on 11 February 2024, with the IO:O instrument on the 2.0-m Liverpool Telescope64 in La Palma on 15 February 2024 and with ULTRACAM65 on the 3.5-m New Technology Telescope at the European Southern Observatory (La Silla) in Chile on 10 February 2024. Pan-STARRS images were obtained in the w band (50âÃâ200-s exposures) and Liverpool Telescope in the r band (32âÃâ120âs), whereas ULTRACAM observed simultaneously in the us, gs and rs bands66 (384âÃâ20âs, with only 24âms between exposures). All images were reduced through standard facility pipelines. For Pan-STARRS, this included subtraction of a pre-TDE reference image and forced photometry at the position of AT2019qiz. In the case of Liverpool Telescope and ULTRACAM, we performed photometry using psf67, an open-source Python wrapper for photutils and other image-analysis routines. We excluded 17 ULTRACAM images affected by poor seeing. We attempted manual subtraction of the Pan-STARRS reference images using psf; however, we found that the extra noise introduced by the subtraction was larger than any detectable variability. As shown in Extended Data Fig. 5, there is no strong evidence for variability on timescales on the order of hours.
Swift/UVOT
UV observations were taken with Swift/UVOT in the uvm2 filter contemporaneously with the XRT observations. We used the uvotsource package to measure the UV photometry, using an aperture of 12â³. We subtracted the host galaxy contribution by fitting archival photometry data with stellar population synthesis models using Prospector68. This standard procedure has been used to analyse previous UVOT observations of TDEs56. We apply Galactic extinction correction to all bands using a E(BâV) value of 0.094 (ref.â69).
The UVOT photometry is shown in Extended Data Fig. 5. Although lacking the resolution of HST to separate the central point source from the host light, the mean measured magnitude of 20.1 is about 0.5âmag brighter than the host level estimated by SED modelling16. The individual measurements exhibit root-mean-square variation of 0.27âmag (Extended Data Fig. 5), possibly indicating variability that would further exclude a nuclear star cluster. The timing of the XRT QPE is marked, coinciding with a possible (but not statistically significant) dip in UV flux as seen in the QPE candidate XMMSL1 J0249 (ref.â13).
AstroSat/UVIT
We observed AT2019qiz with UVIT using the broad filter CaF2 (F148W)50. We processed the level1 data with the CCDLAB pipeline70 and generated orbit-wise images, detecting a bright nuclear source. We performed aperture photometry using the UVITTools.jl package and the latest calibration51, in a circular region of 20âpixels (8.2âarcsec). We also extracted background counts from a source-free area of the image. The background-corrected count rate in the merged image corresponds to a flux density fλâ=â3.16â±â0.97âÃâ10â16âerg cmâ2âsâ1âà â1 or magnitude mâ=â20.49â±â0.03â(AB). We found no statistically significant far-ultraviolet variability between the orbit-wise images. We do not attempt to remove host galaxy flux for the UVIT data, as the field has not been covered by previous far-ultraviolet surveys. SED modelling would require a large extrapolation. Regardless, we expect that the galaxy flux should be negligible at these wavelengths20.
Analysis
Assessing variability
We perform two checks that the X-ray variability corresponds to QPEs rather than random variation. First we compare with physically motivated models of stochastic variability. Referenceâ71 demonstrated a mechanism to produce order-of-magnitude X-ray variability through Wien-tail amplification of accretion-disk perturbations. Their Fig. 3 shows the X-ray light curve of a model with a SMBH mass of 2 Ãâ106âMâ, consistent with AT2019qiz. The light curves are of a visibly different character to our data, with random variability rather than flares of consistent duration and no obvious âquiescentâ level. We ran further simulations using their model and never found a light-curve segment resembling AT2019qiz.
We also take a model-agnostic approach and assume the null hypothesis that the times of the X-ray peaks are random. Drawing a list of 105 delay times from a flat probability distribution between 0 and 60âh and examining every consecutive sequence of eight, we âmeasureâ the standard deviation in delay times to be â¤15% of the mean in only â²0.1% of trials. This is not sensitive to where we place the upper and lower bounds of the distribution. Therefore, we can exclude random peak times at >3Ï confidence.
QPE durationârecurrence time correlation
The data in Fig. 3a show an apparent correlation between the mean duration and mean recurrence time of QPEs from a given source5. An equivalent statement is that QPEs seem to show a constant duty cycle across the population, with previous work indicating a duty cycle of 0.24 ±â0.13 (ref.â5). We reanalyse this correlation including AT2019qiz by performing Bayesian regression with a linear model Tdurationâ= αTrecurrence + β. We find \(\alpha =0.2{2}_{-0.04}^{+0.11}\) (95% credible range), consistent with previous findings5. Comparing this model with the null hypothesis (αâ=â0), we find a change in the Bayesian Information Criterion ÎBIC â 50, indicating a strong preference for a positive linear correlation over the null hypothesis of no correlation.
Disk modelling
We use the time-dependent relativistic thin disk model developed in refs.â19,25. This computes the spectrum of an evolving accretion flow, produced at early times by the circularization of some fraction of the TDE stellar debris. To generate light curves, we follow the procedure of ref.â19 (their Fig. 2). The important input parameters are the mass and spin of the SMBH, the initial disk mass, the diskâobserver inclination angle and the turbulent evolutionary timescale. Also, there are nuisance parameters relating to the initial surface density profile of the disk, which is generally unknown and has minimal effect on the late-time behaviour. As this initial condition is so poorly constrained, we simply consider an initial ring of material (as in ref.â25).
For each set of parameters {Î}, we compute the total (log-)likelihood
$${\mathcal{L}}(\Theta )=-\sum _{{\rm{bands}},\,i}\sum _{{\rm{data}},\,j}\frac{{({O}_{i,j}-{M}_{i,j})}^{2}}{{E}_{i,j}^{2}},$$
(1)
in which Oi,j, Mi,j and Ei,j are the observed flux, model flux and flux uncertainty of the jth data point in the ith band, respectively. For the X-ray data, we compute the integrated 0.3â1.0-keV flux using the best-fit models to the quiescent Swift/XRT and Chandra data, whereas for optical/UV bands, we compute the flux at the effective frequency of the band. We correct all data for foreground extinction/absorption47,69.
The early optical and UV observations do not examine direct emission from the accretion flow, because of either reprocessing72 or shock emission from streams73. We add an early-time component to model out this decay19, with functional form
$${L}_{{\rm{early}}}={L}_{0}\exp \left(-t/{\tau }_{{\rm{dec}}}\right)\times \frac{B(\nu ,T)}{B({\nu }_{0},T)},$$
(2)
in which B(ν,âT) is the Planck function and ν0â=â6âÃâ1014âHz is a reference frequency. We fit the amplitude L0, temperature T and decay timescale Ïdec, as well as the disk parameters. We only include data taken after the peak of the optical light curves.
The fit was performed using Markov chain Monte Carlo techniques, using the emcee formalism74. To speed up computations, analytic solutions of the relativistic disk equations75 were used. The model satisfactorily reproduces all data. The model X-ray light curve shows a slow rise; however, this is completely unconstrained by data and is therefore very sensitive to the uncertain initial conditions of the simulation. After a few hundred days (by the time of the earliest X-ray data in Fig. 4), the disk has spread to large radii and is no longer sensitive to initial conditions. We present the posterior distributions of the physically relevant free parameters in Extended Data Fig. 8. The best-fitting SMBH mass is consistent with all other observational constraints.
We note that a dimensionless SMBH spin parameter aâ¢â>â0 is favoured by the model (although see caveats below), with a peak in the posterior around a⢠ââ0.4â0.5. This constraint originates from the relative amplitudes of the optical/UV and X-ray luminosities, as highlighted in Extended Data Fig. 9. As the optical and UV light curves are well separated in frequency, the properties of the disk at scales rââ³â20rg are tightly constrained. The amplitude of the X-ray luminosity is controlled by the temperature of the inner disk, close to the innermost stable circular orbit. For a given large-scale structure, this radius is determined by aâ¢.
Our disk model parameterizes the colour correction factor fcol in terms of the local disk temperature76, but our posteriors do not marginalize over its unknown uncertainty. Recognizing that modest uncertainties in fcol lead to substantial uncertainties in spin (for non-maximal black hole spins)77, we do not claim a spin measurement here but simply note that a modest spin is consistent with our data. The spin estimates in this model also assume a planar disk that is aligned with the SMBH spin, which is not true in the case of a precessing disk (see next section).
Although the disk temperature profile (and therefore the location of the diskâs outer edge) is tightly constrained from the multiband late-time observations, it is well known that disk temperature constraints only scrutinize the product \({W}_{\phi }^{r}\varSigma \), in which \({W}_{\phi }^{r}\) is the turbulent stress and Σ is the surface mass density. As the functional form of the turbulent stress cannot be derived from first principles, and must be specified by hand, there is some uncertainty in the mid-disk density slope. Our choice of \({W}_{\phi }^{r}\) parameterization is optimized for computational speed75 and is given by \({W}_{\phi }^{r}=w={\rm{constant}}\). Rather than fit for w, we fit for the evolutionary timescale of the disk (which has a more obvious physical interpretation), given by \({t}_{{\rm{evol}}}\equiv 2\sqrt{G{M}_{\bullet }{r}_{0}^{3}}/9w\). We emphasize that this uncertainty has no effect on our constraints on the size of the disk.
With this choice of parameterization for the turbulent stress, the disk density profile (Fig. 4) can be approximated as Σââârâζ, with ζâ=â1/2, for râ=â(2â600)GMâ¢/c2. The density slope is not very sensitive to modelling assumptions, with the (potentially) more physical radiation-pressure-dominated α-disk model having ζâ=â3/4.
Precession timescales
If the SMBH is rotating, any orbit or disk that is misaligned with the spin axis will undergo LenseâThirring precession. This is a possible cause of timing variations in QPEs30. Changes in QPE timing in AT2019qiz are seen over the course of â²8 observed cycles, which would require that the precession timescale Tprec is approximately several TQPE, in which TQPEâââ48.4âh is the QPE recurrence time.
The precession timescale can be calculated following29:
$${T}_{{\rm{prec}}}=\frac{8\pi G{M}_{\bullet }(1+2\zeta )}{{c}^{3}(5-2\zeta )}\frac{{r}_{{\rm{out}}}^{5/2-\zeta }{r}_{{\rm{in}}}^{1/2+\zeta }\left(1-{\left({r}_{{\rm{in}}}/{r}_{{\rm{out}}}\right)}^{5/2-\zeta }\right)}{{a}_{\bullet }\left(1-{\left({r}_{{\rm{in}}}/{r}_{{\rm{out}}}\right)}^{1/2+\zeta }\right)},$$
(3)
in which rin and rout are the inner and outer radii of the disk or orbit, respectively, in Schwarzschild units (see also ref.â78). We assume log(Mâ¢/Mâ)â=â6.3 and investigate the plausible precession period for different values of aâ¢.
The nodal precession timescale for an orbiting body can be estimated by calculating Tprec at the orbital radius (setting Rin ââRoutâââRorb). For aâ¢â=â0.1â0.9, this gives Tprec,orbitâââ(103â104)âÃâTQPE, independent of ζ. Therefore, in the EMRI model, nodal precession is too slow to account for changes in QPE timing over several orbits.
The precession timescale of the disk can be calculated by assuming that it behaves as a rigid body with rinâ=â2GMâ¢/c2, routâ=â600GMâ¢/c2 and a density slope ζ =â1/2 from our disk model. We use the above equation to find Tprec,diskâââ(70â200)âÃâTQPE (for the same range of spins). With a steeper density profile having ζ =â1, this would reduce to Tprec,disk ââ(8â70)âÃâTQPE (because more mass closer to the SMBH enables stronger precession). Therefore, precession can explain detectable changes in QPE timing over the course of several orbits only in the case of a rapidly spinning SMBH (aâ¢ââ³â0.5â0.7) and a steep disk density profile.
With these constraints, attributing the timing residuals primarily to disk precession becomes challenging. The larger the SMBH spin magnitude, the faster an initially inclined disk will come into alignment with the black hole spin axis, damping precession on a timescale â²100âdays for a⢠> 0.6 and M⢠ââ106âMâ (ref.â79). To maintain precession for more than 1,000âdays requires a spin aâ¢ââ²â0.2, in which case the precession is not fast enough to fully explain the timing variations in our data.
We also note that the disk inner radius used in our precession calculation was derived from a planar disk model. In a tilted disk around a spinning SMBH, the radius of the innermost stable circular orbit will differ from the equatorial case. Understanding the effect of disk precession in AT2019qiz will probably require both continued monitoring to better understand the QPE timing structure and a self-consistent model of an evolving and precessing disk that can explain both the multiwavelength light curve and the timing residuals.
Constraints on QPE models
Many models have been proposed to explain QPEs. Disk tearing owing to LenseâThirring precession has been suggested80. This effect has plausibly been detected in the TDE AT2020ocn (ref.â81). However, its X-ray light curve did not resemble that of AT2019qiz or those of other QPEs. As discussed above, it is also unclear whether strong precession will persist until such late times. The X-ray variability in AT2020ocn occurred only in the first months following the TDE.
Gravitational lensing of an accretion disk by a second SMBH in a tight binary could cause periodic X-ray peaks for the right inclination82. However, in the case of AT2019qiz, no signs of gravitational self-lensing were detected during the initial TDE. In this model, a QPE magnification by a factor â³10 requires an extremely edge-on view of the disk, which leads to a shorter duration of the QPE flares. This was already problematic for previous QPEs82 and is more so for the longer-duration flares in AT2019qiz. Moreover, finding a TDE around a close SMBH binary within a very narrow range of viewing angles (â³89.5°) is very unlikely in the small sample of known TDEs, so a strong TDEâQPE connection is not expected in this model.
Limit-cycle instabilities are an appealing way to explain recurrent variability7,83. The recurrence timescale for disk-pressure instabilities depends on whether the disk is dominated by radiation pressure or magnetic fields8, as well as the accretion rate. Our disk model, which is well constrained by the multiwavelength data, gives an Eddington ratio \(\dot{M}/{M}_{{\rm{Edd}}}\approx L/{L}_{{\rm{Edd}}}=0.04\pm 0.01\). Referenceâ26 gives formulae to interpolate the recurrence time for radiation-pressure instabilities, for a given amplitude relative to quiescence. We assume a peak-to-quiescence luminosity ratio of 60, although our analysis is not sensitive to this. Using the prescription for either the intermediate-mass black holes (their equation 33) or SMBHs (their equation 34), we find a recurrence time of about 5,000âdays.
In the magnetic case, we use equation 14 from ref.â8. Matching the observed recurrence time requires a dimensionless magnetic-pressure scaling parameter p0âââ10. However, at this Eddington ratio, the disk should be stable8 if p0ââ³â1. This leaves no self-consistent solution in which magnetic-pressure instabilities cause the QPEs in AT2019qiz. The possibility of a longâshort cycle in recurrence time, and the asymmetric profile of the eruptions3, also disfavour pressure instabilities. We also note that, in disk-instability models, the recurrence time of the instability correlates with SMBH mass. For the known QPEs, there is no apparent correlation in recurrence time with mass (Fig. 3).
The final class of models to explain QPEs involves an orbiting body (EMRI) either transferring mass to an accretion disk or colliding with it repeatedly9,10,11,27,28,30,35,84,85,86. Note that this is very unlikely to be the same star that was disrupted during the TDE: if a bound remnant survived the disruption, it is expected to be on a highly eccentric orbit with a much longer period than the QPEs11. The fundamental requirement for starâdisk collisions to explain QPEs is that the disk is wider than the orbit of the EMRI. The size of the disk in AT2019qiz is well constrained by our analysis and the posteriors of our fit fully satisfy this requirement, at least in the case of a circular disk.
For an orbit with the QPE period to avoid intersecting the disk would require a disk ellipticity eâ>â0.7 (assuming that the semimajor axis of the disk is fixed) and an appropriately chosen orbital inclination. Although some TDE spectra support a highly elliptical disk in the tens of days after disruption87, most can be explained with an approximately circular disk88,89,90. Simulations of TDE accretion disks show a high ellipticity in the days after disruption91, but shocks are expected to circularize the disk over the course of a few debris orbital periods92 (days to weeks), whereas we observe QPEs on a timescale of years after AT2019qiz. An initially highly eccentric disk becomes only mildly elliptical (eâââ0.6) on a timescale of several days (refs.â93,94,95,96,97,98,99,100). Once notable fallback has stopped (before the plateau phase), no more eccentricity will be excited in the disk, whereas turbulence will act to further circularize it, so we expect that the disk in AT2019qiz will be circular to a good approximation.
The case of an EMRI interacting with a TDE disk was specifically predicted by refs.â11,30. The formation rate of EMRIs by the Hills mechanism is about 10â5âyearâ1âgalaxyâ1, about one-tenth of the TDE rate. Because the time for inspiral resulting from gravitational-wave emission (approximately 106âyears) is longer than the time between TDEs (approximately 104âyears), theory predicts that â³1 in 10 TDEs could host an EMRI capable of producing QPEs11,35. This is consistent with recent observational constraints on the QPE rate24.