Curation of high-resolution phylogenetic trees
We combined data from seven previously published sets of somatic phylogenies. Each phylogeny was made up of cells from a single tissue type—haematopoietic stem and progenitor cells (HSPCs; 39 participants)5,6,7,8,9, bronchial epithelial cells (16 participants)10 or liver parenchyma (34 participants)11,12. The phylogenies were built from somatic mutations discovered in whole-genome sequencing of single-cell-derived colonies (HSPCs), single-cell-derived organoids (bronchial epithelium) or LCM from liver48. Details of the research participants, sample acquisition, sequencing and variant calling are provided in the original papers, and the clinical and demographic data are summarized in Supplementary Table 1. Written informed consent was obtained from all participants in the study under approvals from the relevant ethics committees—specific details are available in the original publications5,6,7,8,9,10,11,12.
In total, we collected 103 phylogenies from 89 individuals, with 2 participants from the liver study providing 8 phylogenies each owing to independent sampling from all 8 anatomical segments of the liver in these individuals12. There was a median of 48 samples or clones per individual (range: 11–451). For the studies of the haematopoietic system, we defined 3 categories: (1) fetal and cord blood HSPCs (n = 4; 2 from fetal haematopoietic organs, 2 from cord blood); (2) adult HSPCs (n = 28; 10 from deceased donor bone marrow with no known blood disorder, 3 from individuals with known clonal haematopoiesis, 10 from patients with myeloproliferative neoplasms, 10 from donor/recipient pairs of allogeneic haematopoietic stem cell transplant); and (3) chemotherapy-exposed HSPCs (n = 2, 1 treated twice for Hodgkin’s lymphoma with alkylating-agent-containing regimens; 1 treated with R-CVP, a regimen containing cyclophosphamide and vincristine)—the R-CVP chemotherapy-exposed blood phylogeny was analysed with the ‘adult HSPCs’ group, rather than the ‘chemotherapy-exposed HSPCs’ group as R-CVP did not have significant mutagenic consequences for the HSPC population.
For individuals with single-cell-derived samples, mutations were filtered using similar approaches, with combinations of filters designed to remove germline variants, sequencing artefacts and in vitro-acquired mutations. For individuals from the liver study, collected using laser-capture microdissection, a matched normal was used for mutation calling, with some different downstream filtering steps11,12. The numbers of mutations per sample varied considerably across individuals depending primarily on tissue type, donor age, mutagen exposure (such as smoking, alcohol or chemotherapy), and disease status.
For the single-cell-derived colonies, phylogenetic trees were inferred using a maximum parsimony algorithm. For samples from the liver LCM studies, phylogenetic trees were inferred in a two-step procedure: (1) the set of n-dimensional vectors of variant allele fractions for each mutation were clustered using a hierarchical Dirichlet process11; and (2) the phylogenetic tree describing these clusters was inferred using serial application of the pigeonhole principle49. The robustness of variant calling and phylogenetic tree reconstruction using these methods has been extensively tested, with further details available in the original manuscripts.
Identification of MAVs
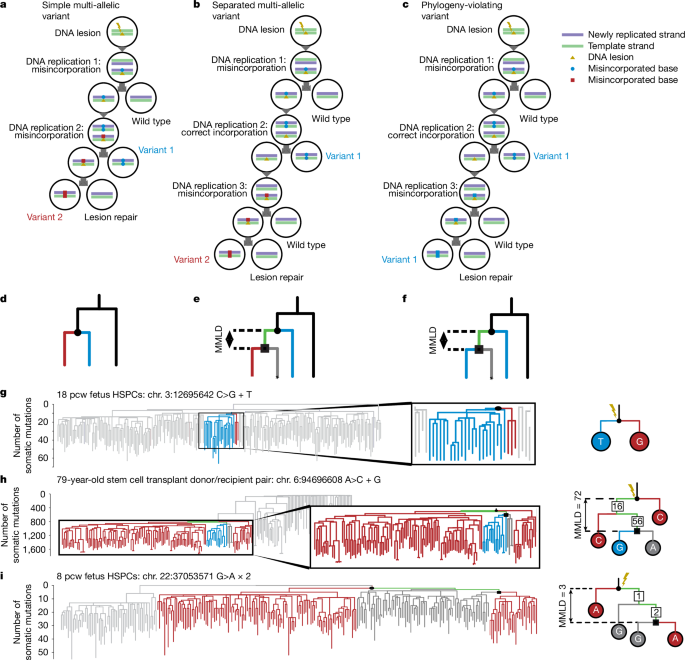
A somatic MAV occurs if a reference base at the same genomic position is mutated to two different mutant alleles in the same individual. For example, there may be evidence of both a C>A and C>T mutation at exactly the same chromosome and position. In the context of the phylogeny data analysed here, these different mutant alleles will be evident in different clones from the same individual.
Within the phylogeny of each participant, we identified mutation pairs with overlap of the mutated locus. For SNV pairs, this is simply identifying SNVs at the same chromosome and position. For deletions and multi-nucleotide variants (MNVs, affecting two or more nucleotides), any degree of overlap was classified as a MAV. Each MAV was classified as simple, separated or fail in a hierarchical manner, on the basis of the orientation of their allocated branches in the phylogeny. If the two mutations had the same parent node (as in Fig. 1d), the MAV was classed as simple, and the parent node classified as the lesion node. If this was not true, but the allocated branch of one mutation fell within the clade defined by the parent node of the other (as in Fig. 1e), the MAV was classed as separated and the parent node that encompassed both mutations was classified as the lesion node. If neither of these criteria were met, the MAV was classed as unrelated. Separated MAVs where the two mutant alleles were separated by two or more subclades with the reference allele had a higher probability of occurring via independent mutation events, as evidenced by the more equal proportion of matching to non-matching phasing comparisons (Extended Data Fig. 3c) and simulation. Therefore, these were reclassified as unrelated, even though a proportion were likely to be caused by a persistent DNA lesion. Unrelated MAVs were likely to have been caused by independent events occurring at the same genomic locus by chance, a hypothesis supported by their mutational signatures which closely resembled the expected signature for this mechanism (Extended Data Fig. 4).
For separated MAVs, the lesion path was defined by starting from the lesion node and working stepwise down the phylogeny along the path containing a mixture of alleles at the genomic position of interest. The last node encompassing two different alleles was classified as the lesion repair node. In most cases this node was only one branch from the lesion node (as in Fig. 1e), but there were occasional examples of longer lesion paths (Fig. 1h). MMLD was calculated as the sum of branch lengths between the lesion and lesion repair nodes.
Identification of PVVs
A PVV is defined here as a mutation that is discordant with the consensus phylogeny. That is to say, the distribution across the phylogeny of clones carrying the mutant allele is not consistent with a single mutation-acquisition event and consistent inheritance in descendants thereafter.
The mutation assignment algorithm assumes that a single variant results from a single, fixed mutational event, after which all daughter cells carry the mutation. For the vast majority of mutations, these assumptions hold true: a branch exists that forms a clade containing only samples with the variant allele (Extended Data Fig. 1a). The point here is that the tree-building algorithm (treemut) assumes that each mutation has occurred exactly once, and finds the single branch with the maximum likelihood for explaining the observed data. For PVVs, these assumptions no longer hold true—with such variants, the assigned mutant clade either: (1) contains a subset of samples without the mutation (Extended Data Fig. 1b); or (2) does not contain all the samples with the mutation (Extended Data Fig. 1c).
The statistical challenge is how to pick out the minority of mutations that do not neatly fit a single acquisition event, amongst up to 100,000 or more somatic mutations per phylogeny. The approach we developed relies on the formal detection of overdispersion of read counts, described in detail below. Before settling on this approach, we experimented with two alternatives:
-
(1)
Identifying mutations that had a low P value calculated by the treemut algorithm. Each branch assignment by treemut comes with an associated P value: the chance of observing the read counts in the data, given a single acquisition event on the assigned branch. However, whatever P value cut-offs we used, there was low specificity and sensitivity for the variants of interest. For example, some indels present in large clades had consistently biased mutant versus wild-type read counts leading to low P values, even when a variant was consistently present only within the assigned clade.
-
(2)
Identifying mutations for which there were either: (1) negative samples within the assigned clade; or (2) positive samples outside the assigned clade. Similarly, this binary approach had poor sensitivity and specificity. It frequently yielded occurrences where there were a few variant reads in a single sample outside the assigned clade (probably sequencing errors or other artefacts), or negative samples within the positive clade where depth was relatively low and there were no reads reporting the variant allele by chance.
Instead, a beta-binomial test for overdispersion proved a powerful approach to detect occurrences where there were in fact two distinct positive and negative populations either within or outside the assigned clade. This approach is analogous to that used to detect true somatic mutations from artefacts in the mutation-calling algorithms50. The reason this approach works better than the other two methods we tried is that the observed data represents a mixture of two binomial distributions—a given sample will report the variant allele at either the base call error rate (if the sample is wild-type) or with probability 0.5 (for a sample with the mutation heterozygously on an autosome). Under a simple mutation assigned to the correct branch of the phylogeny, the two binomial distributions will assort perfectly such that the descendants in the mutant clade all report the variant allele at 0.5 and those outside the clade report it at the base call error rate—there would be no overdispersion beyond this simple partition. For a PVV, however, there will always be a set of samples for which this partition of expected variant allele fraction is violated—either a wild-type subclone within the assigned mutant clade or a mutant subclone outside the assigned mutant clade. A test for overdispersion beyond that expected by chance would report on either scenario and formalizes the statistical inference.
In more detail, this can be detected by testing the read counts of all clades that should theoretically be uniformly positive or negative for the variant, and testing for overdispersion of the observed counts. We quantified the overdispersion by assuming the counts to come from a beta-binomial distribution and finding the maximum-likelihood ρ parameter using the optim() and dbetabinom() functions from R packages stats and VGAM. As DNA lesions causing PVVs must occur on internal branches to allow detection, and will then at least partially follow the phylogeny, we reasoned that such mutations would invariably be allocated to internal branches. We therefore assessed only such internal branch mutations for overdispersion (1) within and (2) outside the clade formed by the assigned node, quantifying the maximum-likelihood ρ parameter for each. PVVs will have a high ρ (empirically set as ≥0.1) for one of these parameters. Additionally, we required strong evidence for either a ‘negative’ subclade within the assigned clade (no variant reads detected with a minimum depth of 13), or a ‘positive’ subclade outside the assigned clade (variant allele frequency (VAF) ≥ 0.25 and ≥3 variant reads). Mutations meeting either pair of corresponding criteria (typically ~1 in 500 internal branch mutations) were considered phylogeny-violating and taken forward for further assessment.
Next, we assigned the putative ‘lesion node’ for each PVV, namely the node containing all samples with the variant. For variants with evidence of overdispersion within the assigned clade (Extended Data Fig. 1b), this was the same as the assigned branch. For variants with evidence of overdispersion outside the assigned clade (Extended Data Fig. 1c), we iteratively travelled node-by-node up through the phylogeny, until there were no positive clades outside the clade defined by that node.
Finally, we iteratively worked down from the lesion node, attempting to define the lesion path through the phylogeny. If caused by a DNA lesion, PVVs should have a specific orientation: at each cell division, one daughter cell will contain the DNA strand resulting from replication opposite the lesion and will therefore have a fixed genotype at the locus of interest (either the reference or mutant allele), which will be consistently inherited by its progeny. This is therefore a uniform subclade with a consistent genotype throughout. The other daughter cell will inherit the lesion itself, and therefore still has the potential for generation of the two alternate alleles, and therefore seeds a ‘mixed’ subclade. The lesion path is defined by the path containing mixtures of genotypes, and the outcome of replication at each cell division defined by the genotype of each uniform subclade arising from this lesion path. Once both daughters of the assessed node are uniform (that is, one contains only mutant samples, the other contains only wild-type samples), the lesion repair node has been reached (Extended Data Fig. 1b). If both daughter nodes of the lesion node contain a mixture of positive and negative clades, this is inconsistent with generation by a persistent DNA lesion (Extended Data Fig. 1c). Such mutations were deemed to have been generated by an alternative mechanism—indeed, mutational signature analysis showed that they were predominantly C>T at CpG sites, consistent with their generation by independent mutations at the same site (Extended Data Fig. 5d,e).
Phasing of MAVs and PVVs to validate their derivation from a single DNA lesion
To assess if the variants of a MAV pair were on the same allele (on the same chromosome copy of a homologous pair), we attempted to phase each variant with proximate heterozygous SNPs. Approximately a third of MAVs had a suitable heterozygous SNP sufficiently nearby for assessment. We extracted heterozygous SNPs within 1 kb of the mutation locus using the VCF files of mutations. Each read-pair crossing both the variant and a heterozygous SNP locus was categorized by the base supported at each (Extended Data Fig. 3b). For phylogenies built with single-cell-derived samples, matching phasing was confirmed if samples carrying each variant of an MAV pair had read-pairs with either (1) the same SNP base and their respective variant base or (2) the same SNP base and the reference base. For phylogenies built with inferred clones (the participants from the liver LCM studies), matching phasing was confirmed only if reads containing each variant base of an MAV pair had the same heterozygous SNP base—that is, the same SNP base phasing with the reference base was insufficient because of the potential inclusion of normal cells in the microdissection. The heterozygosity of the SNP was confirmed in each case. Phasing of the positive subclades of PVVs was similarly assessed. In cases with >2 positive subclades, we considered phasing as confirmed if one or more subclade pair was successfully phased.
Assessment of two independent mutations as an artefactual cause of MAVs
MAVs are rare events, and a potential alternative mechanism for their generation is two independent mutations occurring at the same locus by chance. As independent events, they would be expected to be equally likely in any lineage at any time in their history. This differs from the expectation of MAVs occurring as a result of persistent DNA lesions, which are necessarily in closely related lineages. We therefore aimed to estimate the degree to which there was an excess of closely related MAVs in the data, compared to a null hypothesis that the MAVs result from independent events.
The branch lengths, scaled to numbers of mutations, are estimates for the amount of time passed in that lineage. We could therefore formally assess the proportion of MAVs that would be expected to fall in simple, separated or unrelated orientations by modelling MAV pairs occurring as random independent events within the phylogeny. To simulate this, we randomly selected pairs of phylogeny branches with probabilities proportional to their branch length, repeating this 50,000 times for each phylogeny. Each pair was categorized by the orientation of the two selected branches and compared with the proportions observed in the data. As for the observed data, any pair classified as separated but with two or more intervening negative subclades were reclassified as unrelated. To assess the overall degree to which the set of MAVs may be contaminated by those occurring by chance, we calculated a weighted mean of the simulated proportions in each category, using the total number of MAVs detected in each phylogeny as weights.
Assessment of two independent mutations as an artefactual cause of PVVs
As with MAVs, PVVs may result from two independent mutations at the same locus by chance. In addition, PVVs may theoretically result from spontaneous reversion of a somatic mutation in a subclade of the original mutant clade, a phenomenon that has previously been observed in cases where wild-type cells have a selective advantage. However, the orientation of PVVs did not appear to be that expected from either of these mechanisms. To formally test this, we designed simulations of each, testing all phylogenies with at least one PVV.
-
(1)
Independent mutations at the same site. Similar to the MAV simulations, we randomly selected pairs of branches with probabilities proportional to their branch lengths. Each sample was assigned a depth for the simulated PVV locus according to a random draw from a Poisson distribution with the λ parameter being the overall mean depth in that individual. Samples within clades formed by the selected branches, ‘positive’ samples, were assigned variant counts according to random binomial draws with P = 0.5 and n = depth. Other ‘negative’ samples were assigned variant counts by similar random draws but with P = 1 × 10−6 (the error distribution). Analysis then proceeded as with the data: a single branch was assigned with treemut; if this branch was a terminal branch, there was no further analysis; if it was a shared branch, the counts within and outside the assigned branch clade were assessed for overdispersion using the beta-binomial distribution and the same ρ thresholds as for the data; the lesion node was assigned and the mutation classified as ‘pass’ or ‘fail’. For pass mutations, a lesion node, lesion repair node, MMLD and minimum number of cell divisions was calculated and recorded. We repeated this 10,000 times for each phylogeny and recorded the outcome for all. For all individuals, the majority of independent mutations at the same site were assigned to terminal branches and would not have been included among the PVVs in the dataset. A proportion were assigned to shared branches but did not meet the filtering criteria for a PVV. Notably, very low proportions fell in an orientation consistent with generation by a persistent DNA lesion (‘pass’ PVVs: median, 0.018; range, 0.002–0.12), with the lowest proportions in those phylogenies with the highest numbers of ‘pass’ PVVs in the data. We then compared the ‘pass’ PVV numbers as a proportion of the total detectable PVVs in the data and simulations. To assess the overall degree to which the set of PVVs may be contaminated by those occurring by this mechanism, we calculated a weighted mean of the simulated ‘pass’ or ‘fail’ proportions, using the total number of PVVs detected in each phylogeny as weights (Fig. 2g).
-
(2)
Spontaneous somatic reversion of somatic mutation. For a somatic reversion event to be evident in a phylogeny, there must first be a somatic mutation, and subsequently a reversion event within the captured lineages of the mutant clade. The probability of a branch giving rise to a captured somatic reversion is therefore proportional to the product of the branch length and the sum of branch lengths within that clade. Intuitively, this can be thought of in these terms: a long branch has lots of mutations with the potential for reversion, and many subsequent long branches within that clade gives much time and many independent lineages for those mutations to revert. Therefore, we selected branches with probabilities weighted by this product. The reversion branch was then chosen from branches within the selected branch clade, again with probabilities weighted by their branch lengths. Simulation then proceeded analogously to the ‘independent mutation’ simulation, but with positive samples defined as those within the somatic mutation clade, but not in the reversion clade. We repeated this 2,000 times for each phylogeny and recorded the outcome of each (Fig. 2f). Interestingly, only a minority of somatic reversion events were detected as PVVs (median proportion, 0.173), as they often result in large positive clades with a single negative sample. These have little impact on the inferred ρ value, as such occasional negative samples are not unexpected with binomial sampling of the variant and wild-type alleles as occurs with sequencing of heterozygous sites. However, as expected, almost all those detected were classified as ‘pass’ PVVs.
Assessment for LOH as an artefactual cause of PVVs
PVVs may result if a cell containing a somatically acquired mutation loses the mutant allele through say whole chromosome deletion or smaller-scale LOH mechanisms such as mitotic recombination and focal deletion. To exclude this as the cause of the observed PVVs, we used two complementary approaches. First, we applied ASCAT, an allele-specific copy number algorithm51 to each sample in turn, using a phylogenetically unrelated sample from the same individual as the matched normal. For each PVV, we defined the negative subclades and determined the minor allele copy number at the mutant locus for each sample within that clade. The mean value across negative subclade samples was rounded to the nearest integer: a value of 1 was classed as ‘no LOH’ (heterozygosity is maintained) and 0 was classed as ‘LOH’. A small proportion of PVVs (10 out of 426, 2.5%) were shown to be caused by LOH (Fig. 2e), and were excluded from further analysis.
It is also formally possible that short sub-kilobase LOH events were missed by ASCAT. We therefore used a second approach to directly interrogate sequencing reads and confirm that samples in the negative subclade included reads from the chromosome copy with the mutation. To do this, we first phased the mutation with nearby heterozygous SNPs by interrogating the reads from samples with the mutation. This was possible in approximately one third of cases (Extended Data Fig. 5a). We then interrogated colonies from the negative subclade to confirm the presence of reads reporting the SNP allele from the parental chromosome that carried the mutation.
Sequencing of only the wild-type allele by chance is another potential cause of a PVV, particularly if the negative subclade is a single sample with low depth (although a minimum depth of 12× was required in the PVV identification stage). This read-based assessment also excludes this mechanism. Where assessable, the read-based LOH assessment agreed with the result from ASCAT in all but one case (Extended Data Fig. 5b).
Assessment of incorrect phylogeny structure as an artefactual cause of PVVs
For all PVVs, there is an alternative phylogeny structure with which the PVV would in fact be consistent (Extended Data Fig. 1d). To confirm that PVVs did not simply result from phylogeny inference errors, we counted the mutations in conflict with the structure suggested by the PVV (in most cases this is the same as the MMLD), and confirmed that they were robust. This required ensuring that the mutation calls themselves were not false positives (manual inspection of sequencing alignments) and that the set of colonies reporting the mutations was correctly assigned (Extended Data Fig. 1e). In addition, we manually checked up to five such mutations for a large number of PVVs, confirming that they validated the consensus phylogeny as expected. In all but one case, there was more than one somatic mutation that convincingly confirmed the consensus phylogeny—thus, for these branches, there was considerably more evidence for the original phylogeny than for the alternative phylogeny suggested by the single PVV.
We further looked into all PVVs with <5 mutations confirming the consensus phylogeny, with a total of 19 PVVs meeting this criterion. Eleven out of nineteen were highlighted as potentially low confidence by either the MPBoot bootstrap support, read count bootstrap support or alternative tree-building approaches discussed in the following paragraphs. We visualized the remaining eight mutations, all of which appeared genuine PVVs caused by prolonged DNA lesions rather than any other mechanism. In all eight cases there was more support for the consensus phylogeny than for the alternative phylogeny.
The consensus phylogeny, as relates to each PVV, is defined by the clades within the ‘lesion node’ and the ‘lesion repair or loss node’. If these are robust, then this suggests that the phylogeny is correct and that the PVV is the exception. We therefore assessed the robustness of these nodes using three different approaches: (1) bootstrap support for the nodes using the bootstrap support values from the MPBoot algorithm; (2) bootstrap support for the nodes using bootstrapping of the read count matrices; and (3) the nodes being identical when the phylogenies are reconstructed using alternative algorithms.
MPBoot bootstrap support for the lesion node and lesion repair node
The MPBoot algorithm used to construct the phylogenies gives bootstrap support values for each node52. Therefore, for 440 of 501 PVVs (those for which these bootstrap support values were available, all within the haematopoietic phylogenies), we examined the bootstrap support values for the lesion node/lesion repair node for each PVV. This showed that for 90% of PVVs both lesion node and lesion repair node had bootstrap support values ≥98%, and for 96% of PVVs, both had support values 80% (Supplementary Fig. 1a). Only 15 out of 440 PVVs (3.4%), across 9 different nodes, had <80% support for either node, these are discussed further below. This demonstrates the high confidence in relevant phylogeny structures.
Read count bootstrap support for the lesion node and lesion repair node
An alternative bootstrapping approach is to bootstrap the variant read counts across all samples and mutation sites, as previously described7,32. In this approach, we use the partially filtered mutation set and bootstrap the sequencing read counts for each colony at each locus before subjecting this raw read count data to the same filtering and phylogeny-building algorithms as the original data, with 200–250 replicates per individual. This is computationally intensive and therefore was applied to only 9 blood phylogenies, which accounted for 202 out of 501 PVVs. Again, this suggested that 93% of PVVs had 100% bootstrap support for both lesion node and lesion repair node, and only 7 out of 202 assessed PVVs (3.5%) had less than 80% bootstrap support for either node, discussed further below (Supplementary Fig. 1b,c). All but one of these had also been identified as low confidence by the MPboot bootstrap support measure.
Support for the lesion node and lesion repair node from alternative phylogeny algorithms
Another way to assess the robustness is to compare the phylogeny generated by MPBoot to other phylogeny-reconstruction approaches to see if phylogenies are generated with identical lesion node and lesion repair node clades. Overall, the three algorithms gave very high measures of concordance—for example, Robinson–Foulds similarities for MPBoot versus IQ-tree and MPBoot versus SCITE were almost all >0.95; quartet similarities were almost all >0.99 for the two pairwise comparisons (Table S4).
For 3 of the blood datasets accounting for 439 out of 501 PVVs we compared the clades defined by the lesion nodes and lesion repair nodes in phylogenies generated by IQ-tree53, and where feasible, SCITE54. The output for the SCITE algorithm frequently generated phylogenies with polytomies at the site of PVVs, causing fairly frequent discrepancies in the nodes despite the presence of the underlying inconsistent genotypes. Therefore, for the remainder of the analysis we focussed on the IQ-tree phylogenies. For 93% (409/439) of PVVs, the lesion node and lesion repair node were identical. For the remainder, we re-ran the PVV detection algorithm using the trees generated by the IQ-tree algorithm, and confirmed that although the clades had subtle differences (sometimes due to removal of a low-coverage sample), 18 out of 30 of the remaining PVVs were still called. The remaining 12 mutations affected 8 different nodes, and again 8 of the 12 overlapped with those identified as low confidence by the MPBoot bootstrap confidence approach.
PVVs highlighted as possible low confidence
Altogether, 19 out of 440 (4.3%) blood PVVs were identified as potentially low confidence by one or more of the above approaches. We manually inspected each of these to understand which of these were incorrectly called, and the probable underlying reasons. Several patterns emerged:
Scenario 1. Owing to the PVVs, there is a degree of equipoise as to the true underlying phylogeny; therefore an alternate configuration for the phylogeny may be produced from bootstrapping or alternative phylogeny reconstruction. However, there remains no single phylogeny that fits all mutations, and one or more PVVs is always present. In this scenario, there may be question marks over which mutations follow the true phylogeny, and which represent PVVs generated by persistent lesions. In several cases, the original MPBoot phylogeny was still best supported (Supplementary Fig. 2a,b). However, in one example, highlighted by all three approaches, the original phylogeny was supported by three mutations, but the alternate phylogeny was supported by four mutations (Supplementary Fig. 2c). This made the alternate phylogeny more likely. In addition, the mutational profile of the three mutations that became PVVs according to the alternate phylogeny were more in keeping with the typical PVV profile, as all were C>T at CpT sites. This suggested that the IQ-tree was the correct configuration. We therefore removed the original four PVVs and replaced them with the three from the IQ-tree analysis, and updated the consensus tree structure accordingly.
Scenario 2. An alternative phylogeny is generated which highlights a potential issue with the original phylogeny, and that there is in fact unlikely to be a prolonged DNA lesion. The reasons for the incorrect original phylogeny include:
-
(1)
Low sample coverage in one or more samples leading to incorrect phylogeny building (Supplementary Fig. 2d,e).
-
(2)
Inappropriate inclusion of a mixed colony in the MPBoot phylogeny which therefore cannot be correctly placed on the phylogeny (Supplementary Fig. 2f).
-
(3)
Probable independent acquisition of the same mutation leading to an incorrect original phylogeny (Supplementary Fig. 2g,h). In one case (the chemotherapy phylogeny), this mutation is a driver mutation in PPM1D, showing an example of convergent evolution (Supplementary Fig. 2h).
Scenario 3. The reason for the low bootstrap support from MPBoot is unclear and the PVV appears correctly identified on manual inspection (Supplementary Fig. 3a–d).
As a result of this detailed interrogation of 440 out of 501 PVVs, a total of 10 PVVs were removed, and 3 added to the final mutation set. Overall, this demonstrates that, within the limits of the analysis, the vast majority of PVVs (98%) are robust. However, not all alternative mechanisms can be excluded for each individual PVV.
Coverage, spectrum and distribution of branch-creating mutations
As final checks, we assessed the coverage, spectrum and genomic distribution of the mutations that created branches carrying PVVs, compared these patterns to other mutations on the phylogenetic tree. The reason for these checks was the possibility that the branch-creating mutations may represent low-coverage or low-confidence mutations or other mutation-calling artefacts that would falsely affect the tree-building algorithms.
We found that the ~8,000 branch-creating mutations had an almost identical mean coverage to the mutation set as a whole. The mutational spectrum of the 8,000 branch-creating mutations was the same as the full mutation set, suggesting that they were not a distinct set of artefacts, which tend to have specific mutational profiles. Finally, we compared various genomic features of these branch-creating mutations to the overall mutation set. Although for 2/37 there was a suggestion of a weak association (distance to ALU repeat region, q value = 0.03; distance to z-DNA motif, q value = 0.06), there was no obvious relationship visually. Overall, we believe the vast majority of the branch-creating mutations to be genuine and the trees therefore robust.
Inference of expected MAV mutational signatures
We aimed to identify the most likely mutagenic processes to cause the MAVs observed in the bronchial epithelium and PX001 (chemotherapy-exposed HSPC) phylogenies. We started with the SNV mutational signatures that were inferred as present in each tissue from the original studies5,6,7,8,9,10,11,12 (Extended Data Fig. 6b–d, left). For the bronchial epithelium and liver, these signatures were previously extracted using a Bayesian hierarchical Dirichlet process as implemented in R package HDP (https://github.com/nicolaroberts/hdp)55. We used the same package to extract mutational signatures from phylogeny PX001, the chemotherapy-exposed case, using mutations on individual branches as single samples. For each signature, an expected MAV signature could then be inferred as proportional to the product of the context-specific relative likelihoods of the two SNVs in each MAV, weighted by the abundance of that context in the human genome. Accordingly, we calculated the expected MAV signatures resulting from each extracted mutational signature in bronchial epithelium, liver and blood (Extended Data Fig. 6b–d, right) and compared this to the observed MAVs.
Inference of expected PVV mutational signatures
For each potential alternative mechanism that may generate a PVV, a specific, predictable mutational signature is expected. Going through each in turn:
-
(1)
Two independent mutations at the same site. The expected signature reflects the square of the likelihood of a given mutation at a specific trinucleotide context, weighted by the frequency of that context in the human genome. Raw mutational signatures can be converted into likelihood signatures by correcting for the trinucleotide frequency. Owing to the low abundance of CpG sites in the human genome, this predominantly has the effect of demonstrating the high likelihood of C>T mutations at CpG. This likelihood signature is squared to reflect the fact that the same mutation has to occur twice at that site, before being multiplied by the trinucleotide frequencies to get the expected abundance of such events across the genome. For adult HSPC signature, this results in a signature dominated by C>T mutations at CpG sites, particularly ACG trinucleotides (Extended Data Fig. 5d(i)). This signature is very similar to that observed for the 109 adult HSPC PVVs that are not in an orientation consistent with generation by a persistent DNA lesion, suggesting that these are predominantly caused by this mechanism (cosine similarity, 0.9; Extended Data Fig. 5e). As a further check on the possibility of chance co-occurrence of the same mutation, we assessed the numbers and spectrum of mutations occurring at the same site in different research participants. Across 27 adult haematopoietic phylogenies, with 5,733,980 mutations among them, there were a total of 34,862 that were shared by 2 or more individuals. We found a very consistent rate of sharing of 2.5 × 10−9 of all mutation pairs when both individuals had mutational profiles dominated by the blood signature (calculated as number of shared mutations/[total mutations in individual 1 × total mutations in individual 2]). As expected, the mutational spectrum of these shared mutations was dominated by C>T transitions in a CpG context (Extended Data Fig. 5f), remarkably similar to the predicted spectrum of chance co-occurrence of mutations in blood cells (Extended Data Fig. 5d(i)) and different to the spectrum observed for PVVs in the same individual (Fig. 3c).
-
(2)
Spontaneous reversion of a somatic mutation. For a spontaneous reversion to occur, a mutation at a given trinucleotide context must, at a later time point, be followed by the reverse mutation (at the same context)—for example, C>T at ACG must be followed by a T>C at ATG. The likelihood of this occurring is proportional to the product of the likelihood of the original mutation and the likelihood of the reversion mutation. The expected signature is therefore this likelihood, multiplied by the trinucleotide frequencies. For the adult HSPC signature, this reveals a signature with a dominant peak at T>C mutations at ATG sites, reflecting the high likelihood of the reversion mutation (Extended Data Fig. 5d(ii)).
-
(3)
LOH, biased allele sequencing or incorrect phylogeny. All of these mechanisms of PVV generation are agnostic to the identity of the original mutation. Therefore the expected mutational signature of such PVVs should reflect that of the overall tissue signature (Extended Data Fig. 5d(iii)).
The observed PVV signature (Fig. 3c) is clearly distinct from any of these predicted signatures (cosine similarities: 0.15, 0.3, 0.62 for independent mutations, spontaneous reversion and other mechanisms respectively). This supports the premise that these are caused by a specific mutational process.
Inference of mean lesion duration
The C>T PVVs in the HSPC phylogenies had a consistent signature and broadly consistent MMLDs. We therefore hypothesized that these PVVs are caused by a single underlying lesion. The MMLD of the C>T PVVs has a median value of 21, corresponding in chronological time to ~1.3–1.5 years. However, this value may not be a good estimate of the true lesion durations for three main reasons:
-
(1)
For each PVV, the MMLD is a minimum of the true lesion duration.
-
(2)
Lesions captured as PVVs may represent the longest durations from the underlying distribution of lesion durations.
-
(3)
The duration of detected PVVs is dependent on the phylogeny structure. For example, if there was only one branching region of the phylogeny suitable for capturing PVVs, any detected PVVs would have the same MMLD, defined by the phylogeny.
We designed an ABC model to account for these factors and estimate the true mean duration of the underlying lesion. This used only the four phylogenies from the older individuals from the normal ageing haematopoiesis dataset5, as these had some of the largest and richest phylogeny structures (and therefore the least potential bias), and had substantial numbers of C>T PVVs per individual (range: 8–73).
Simulating complete HSC population phylogenies with lesions
The simulation framework started with 40 simulated ‘elderly’ complete haematopoietic stem cell populations using parameters drawn from the posterior distribution of the ABC in our normal haematopoiesis study5, an HSC population size of 100,000, and an age of 75. These populations reflected the diversity of oligoclonality found in the four elderly phylogenies (Extended Data Fig. 11a). Within each of these populations, lesions were randomly introduced with lesion durations drawn from a gamma distribution with shape = 1, and mean varying from 0.5 years to 5 years, µ = {0.5, 0.6, 0.7 … 5}. For each population and lesion duration, sufficient lesions were introduced to ensure that at least 60,000 PVVs were theoretically detectable within the complete phylogenies. For longer lesion times, ~2 × 106 lesions were sufficient, but for short lesion times (µ = 0.5 years), introduction of >3 × 107 lesions was sometimes necessary. These 40 complete aged HSC populations, each with 47 different sets of 60,000 potentially detectable PVVs caused by lesions of varying duration, formed the starting point for the subsequent simulations.
Simulating the data
We then performed simulations to mirror the data. For each simulation run, 4 of the aged HSC populations were randomly selected to represent the four elderly phylogenies in the data, and a single mean lesion duration was chosen from µ = {0.5, 0.6, 0.7 … 5}. Each selected population was then randomly down-sampled to the size of the actual phylogenies (328 tips for KX003, 922 tips for KX004, 315 tips for KX007 and 367 tips for KX008). We then iterated in random order through the potentially detectable lesions present in the complete phylogeny (generated from the simulations of persistent lesions with the chosen value for µ) to see if they remained detectable in the down-sampled phylogeny. Typically, only ~1 in 1000 remained detectable. Once adequate lesions were detected to represent those found in the data (33 for KX003, 80 for KX004, 9 for KX007 and 22 for KX008), the simulation stopped. In 41% of cases, despite assessing all 60,000 PVVs in each phylogeny, the total number detectable remained somewhat fewer than the data, though >99% had at least 100 of the targeted 129 PVVs. Each down-sampled tree was then rescaled to molecular time using the get_elapsed_time_tree function from the rsimpop package, and the MMLD of each captured PVV recorded. As with the data, any lesion with MMLD > 200 was removed from the set. Finally, a gamma generalized linear regression model was used to estimate mean and dispersion parameters on the combined MMLD set, using the glm function from the R package ‘stats’. The dispersion and mean of the MMLD distribution clearly varied according to the mean duration of the underlying distribution (Extended Data Fig. 11b,c), although the parameters plateaued somewhat once the mean lesion duration reached 3–4 years.
Assessing the performance of the ABC framework
We next assessed the performance of the new framework in recovering the true lesion durations from simulated data. We therefore simulated 4 additional elderly phylogenies, and again introduced simulated lesions of varying duration drawn from a gamma distribution of varying mean, µ = {0.5, 0.6, 0.7 … 5} and shape = 1. As before, we then down-sampled the phylogenies to the size of those from the data and determined if each PVV from the full phylogeny remained detectable, and its MMLD. For each mean lesion duration, we sampled MMLDs from the complete set such that the total numbers were the same as the data. Finally, for each value of µ we performed the parameter inference using the the abc function from the ‘abc’ package (https://doi.org/10.32614/CRAN.package.abc), using a tolerance of 0.05 and the ‘rejection’ method, meaning that no regression step was performed. This showed that the simulations and inferences performed broadly well across the range of mean lesion durations (Extended Data Fig. 11d,e), with the ‘ground truth’ mean lesion duration falling within the 95% posterior intervals of the inferred values in 45 out of 46 cases.
Performing the parameter inference
Having established that the framework performed as expected on simulated data, we ran the ABC inference on the observed data, again using the abc function from the abc package and the same settings. This produced the approximate posterior distribution of the true mean lesion duration (Fig. 5a).
Posterior predictive checks
We performed posterior predictive checks, drawing values of the mean lesion duration parameter µ from the posterior distribution and running additional simulations. In this way, we performed 230 additional simulations. The summary statistics from these produced distributions of summary statistics, which, in contrast to the summary statistics from the prior (Extended Data Fig. 11f), closely matched the data (Extended Data Fig. 11g).
Inferring the average number of lesions per cell at any time
In our ABC framework, we recorded how many lesions needed to be introduced in order to generate sufficient PVVs to match the data. We also know the overall amount of ‘lineage time’ of the complete HSC population into which lesions are simulated, which is the sum of all the edge lengths (scaled to days). Using this data, and the distribution of lesion durations, we can readily infer the average number of lesions expected in any given cell at any given moment in time. We therefore created a posterior distribution for this parameter, using the parameters from the accepted set of simulations from the abc step (Extended Data Fig. 11h). One limitation is that the sensitivity for PVVs varies by phylogeny clonal structure, and this was not accounted for in the model: lesions were simply added to a phylogeny until sufficient PVVs were detected to match the data. Therefore, for a simulated ‘insensitive’ clonal structure the implied lesion density may be artificially high if it were trying to generate the same number of PVVs as a more sensitive clonal structure from the data. However, it at least gives a broad sense of the range in which the true value may sit.
Detection of lesion segregation
We used the ‘calculate_lesion_segregation’ function from the R package MutationalPatterns v3.01 (https://bioconductor.org/packages/MutationalPatterns)56 to assess for lesion segregation in each individual branch from each phylogeny. As reported in the DEN-exposed mouse model study15, we used the binomial, Wald-Waldowitz and rl20 tests—branches were considered positive if the rl20 was ≥6 and at least one of the binomial or Wald-Waldowitz tests had a Benjamin–Hochberg-adjusted P < 0.05.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.