Probing the Kitaev honeycomb model on a neutral-atom quantum computer

Experimental system

We use the experimental apparatus previously described in refs. ^6,9,12,38,57, with key upgrades that enable efficient digital simulation of Hamiltonian systems. ⁸⁷Rb atoms are stochastically loaded from a magneto-optical trap into programmable configurations of 852-nm traps generated with a spatial light modulator (SLM; Hamamatsu X13138-02), and then rearranged with 852-nm moving traps generated by a pair of crossed acousto-optic deflectors (AODs; DTSX-400, AA Opto-Electronic) to realize defect-free arrays^38,58,59. We image atoms with a 0.65-numerical-aperture objective (Special Optics) onto a complementary metal–oxide–semiconductor camera (Hamamatsu ORCA-Quest C15550-20UP). The qubit state is encoded in m_F = 0 hyperfine clock states of the ⁸⁷Rb ground-state manifold (coherence time T₂ > 1 s (ref. ⁶)), and 2-photon Raman excitation is used to drive fast, high-fidelity single-qubit gates^6,60. We use both a global Raman path to drive rotations on the entire array and local Raman light generated by two-dimensional AODs and sent through the objective⁹. The local single-qubit Raman gates are realized through two different schemes⁹, either through local Z rotations or local X rotations. For the feedforward local pulses and the local pulses used to prepare patterns of fermions (in Figs. 4 and 5), we use local single-qubit Z gates⁹. For the measurement-based state-preparation circuit and final local measurement basis rotations, we use local Raman X rotations, as described in more detail in ref. ⁴¹. To realize high-fidelity entangling gates^{12,43,61,62,63}, we excite the atoms to the n = 53 Rydberg state using a 2-photon scheme with 420-nm and 1,013-nm lasers⁶⁴. We use a closer intermediate-state detuning of 3.3 GHz compared with our previous work^9,12. This allows us to address a larger gate region and reduce detuning inhomogeneity from the 1,013-nm light shift to improve uniformity of the entangling gates across the array, at the cost of slightly higher scattering¹². Between entangling gates, we rearrange the atoms dynamically with the AOD traps to achieve any-to-any connectivity^6,9.

In our experimental layout (Extended Data Fig. 1a), the hexagonal plaquettes of the honeycomb model are embedded in a rectangular atom array with four rows. In these experiments, we use three separate zones: entangling, storage and readout⁹. Atoms are first sorted in the storage zone, then transported into the entangling zone before the start of the experiment. We employ an upgraded sorting algorithm, which, compared with our previous algorithm³⁸, has an additional final step to fill individual defect sites from a small atom reservoir (more details in ref. ⁴¹). For the state-preparation circuit, we perform mid-circuit measurement^{43,65,66,67,68,69} of the ancilla qubits, by bringing them to a spatially separated readout zone far away (about  150 μm) from the entangling zone and imaging them with a single, local 780-nm imaging beam⁹. The fidelities of individual components such as single-qubit gates and two-qubit CZ gates in this work are roughly similar to our other works^9,12, except for the local imaging fidelity, which was lower during data taking owing to degrading trap laser power (about 96–97% compared with 99.8% in ref. ⁹).

Tunable entangling phase gates

A key upgrade to our experiment, enabling efficient digital evolution, is the use of tunable entangling controlled-phase gates (denoted CPHASE or CP) characterized by the angle θ (normalized such that θ = 1 is the CZ gate). We implement each CP gate using a single Rydberg laser pulse with constant intensity and a phase profile given by the cosine function, \(A\cos (\omega t+\varphi )\), and a constant two-photon detuning δ (ref. ¹²). These parameters are numerically calculated for each θ using optimal control methods^12,70,71. For Floquet evolution, we combine two CP gates with global single-qubit X operations to realize entangling gates of the form

which are related to CP gates through single-particle terms. This approach is not only a robust way to remove the single-qubit terms but also ensures that atoms in the entangling zone that are not undergoing gates do not pick up a spurious phase.

To calibrate the entangling gates, we adapt an approach from ref. ⁷², which allows for measuring the entangling phase (Extended Data Fig. 2c). We first initialize a pair of atoms, one in \( +\rangle _y=(| 0\rangle +\rmi| 1\rangle )/\sqrt2\) and the other in \(| 0\rangle \). Then we apply a series of gates to the atom pair, which causes the atom in \( +\rangle _y\) to acquire a phase according to the magnitude of the entangling phase. Finally, we apply a single-qubit rotation in the appropriate axis to the atom initially prepared in \( +\rangle _y\) to bring it to \(| 0\rangle \) for a perfect gate. After expelling atoms in \(| 1\rangle \) with resonant push-out light, both atoms should be present only if the gates are perfect. This benchmarking sequence is sensitive to both the entangling phase θ and loss from the gate operation.

To calibrate the gates, we run this circuit with a fixed number of entangling gates, and scan gate parameters to optimize the gate performance on the experiment, in a similar approach to our CZ gate calibration described previously in ref. ¹². We measure the return probability after 20 CPHASE gates, for different values of the entangling phase (Extended Data Fig. 2d). The return probability is higher for smaller entangling phases, owing to the shorter gate duration and reduced average Rydberg population.

Automated calibration

Owing to the large range of gate angles used in this work, we employ automated calibration routines that enable convenient calibration, using either an automated version of the parabola scan method previously used¹² or a Nelder–Mead optimization algorithm⁷³ adapted for noisy data⁷⁴. In addition, we perform automated calibration of the Rydberg beams, owing to the importance of beam homogeneity for realizing uniform gate angles across the array. We use a flat top-hat intensity profile generated using an SLM to maximize homogeneity across the array³⁸. To address local deviations in the beam intensity, we use pre-calculated ‘peak correction’ phase masks which, upon addition to the base hologram, realize localized intensity peaks (Extended Data Fig. 2f). We use automated noisy Nelder–Mead optimization to sequentially adjust both Zernike and peak corrections on the SLM. An example calibration is shown in Extended Data Fig. 2g, where the peak-to-peak variation in beam intensity between rows in the array (as measured by the light shift on the hyperfine qubit) decreases throughout calibration. This active optimization procedure significantly improves the homogeneity of the intensity profile across the rows (Extended Data Fig. 2h), and can be used in combination with passive approaches for removing aberrations^38,75,76.

Measurement-based preparation of topological states

We begin our experiments by efficiently preparing a long-range entangled, topological state on a cylinder, which forms the basis for all subsequent explorations. The high-level description of the procedure is presented in Extended Data Fig. 3a,b. First, we prepare a ZXXZ surface code state^39,77 on one of the data-qubit sublattices (black sites), using entanglement operations with ancilla qubits to project the data-qubit state into an eigenstate of the weight-4 ZXXZ operators. Concretely, we put the ancilla qubits in the \( 0\rangle _\rma+ 1\rangle _\rma\) state and perform a sequence of CZ gates, with data qubits in the appropriate bases, which realizes the \( 0\rangle _\rma+\rmZ_1\rmX_2\rmX_3\rmZ_4 1\rangle _\rma\) state, where the numbers label the data qubits along an example ZXXZ operator (Extended Data Fig. 3a). The subsequent measurement of the ancilla qubits in the X basis fixes the parity of the ZXXZ operators on the data qubits. The measurement outcomes and, thus, the projected operator parities are random (up to certain constraints on their products). A feedforward step, acting on the same sublattice, ensures that all parities end up being +1, which corresponds to the subspace with the ground state of the Kitaev model⁷⁸. For the fermion dynamics, this ensures that no magnetic fluxes are present.

The order of entangling bases we use is Z, X, X, Z, and as all qubits are initially in the \(| 0\rangle \) state, we can omit the first Z measurement; the resulting circuit for this part is depth 3. These weight-4 ZXXZ operators are grown to weight-6 ZYXZXY operators by performing parallel controlled-Y (CY) operations between the entangled sublattice (black) and the one remaining in the \(| 0\rangle \) state (green). The resulting weight-6 operators are equivalent to the plaquettes W_p = ZYXZYX up to the ZZ-link operators (Extended Data Fig. 3a). However, the structure of the circuit ensures that the ZZ-link terms are +1 and, thus, can be freely multiplied into other operators. As a result, this depth-4 circuit efficiently prepares the fermionic vacuum sate, or equivalently the \(\rmA_\rmZ^\rmI\) ground state of the Kitaev honeycomb model³. Such measurement-based methods can be used for preparing a wide range of topological states in finite depth^8,79,80.

The experimental implementation of this sequence is shown in Extended Data Fig. 3c–e. Initially, the ancilla qubits are located in movable AOD traps and the data qubits are in stationary SLM traps. The ancilla qubits are reconfigured and then entangled with data qubits in the correct basis. The first entanglement step includes the periodic boundary direction and has an additional component where the top row of ancilla qubits is entangled with the bottom row of data qubits. We perform this step first so that all other qubits can be in state \(| 0\rangle \), avoiding additional errors owing to Rydberg excitations.

To realize mid-circuit measurement, the ancilla qubits are transported to the readout zone and locally imaged⁹. The measurement outcomes are then used to perform real-time decoding and feedforward. The feedforward correction is applied before the parallel CY operations (Extended Data Fig. 3e).

For the feedforward corrections, we use a field-programmable gate array (Xilinx ZCU111), to gate on and off 32 local single-qubit Z gates applied across 1 sublattice of the array (Extended Data Fig. 3d). An example of mid-circuit decoding and feedforward is shown in Extended Data Fig. 4a. The decoding algorithm uses single-site Z gates, which flip the two vertically adjacent plaquettes, to pair the −1 results in each column by pushing the −1 values until another one is encountered. The initial site for each column and the direction of the pushing procedure is randomized to avoid biasing any given row of plaquettes. The decoder can additionally be modified to prepare an initial state with a deterministic pattern of ±1 plaquette values, as long as the configuration does not violate parity constraints. In Fig. 5, we use this flexibility to initialize different states with fewer local pulses than naively necessary: if a single-qubit gate pattern used to initialize the fermion sites flips an even number of plaquettes per column, we can pre-compensate for those flips in the decoding step (Extended Data Fig. 9a).

In Extended Data Fig. 4d,e, we numerically explore various constant-depth circuits realizing the long-range entangled state of interest. The method we employ in this work significantly outperforms other approaches, including the direct measurement of the hexagonal plaquettes.

Decoding error detection

The product of ancilla measurement outcomes in every column must be even as the plaquettes in any column multiply to strings enclosing the cylinder that are composed of Z operators only (Extended Data Fig. 4b), which are fixed to be +1 owing to our initial product state. This constraint can be used for error detection. In particular, whenever there are an odd number of −1 ancilla measurement results in a given column, we know that an error must have occurred during the state-preparation circuit. Utilizing this decoding postselection method, we observe that all lengths of loops improve in value, as shown in Extended Data Fig. 4c.

Throughout this work, we find that error detection is not necessary for achieving the main results but consistently improves data quality. We define a decoding threshold for the number of columns that can have odd ancilla parity. For example, a decoding threshold of 0 means that all 8 columns have the correct even ancilla parity. In Fig. 3a, we use a decoding threshold of 1, and in Fig. 3c, we use a decoding threshold of 2. In Fig. 4c, we do not use decoding postselection, and in Fig. 4e, we use a decoding threshold of 4. For Fig. 4f, we use a decoding threshold of 1, except for the full exchange final state, for which we use a decoding threshold of 0. Finally, for Fig. 5e,f, we use a decoding threshold of 1.

Postselection based on atom loss

We utilize a state-selective qubit readout, described in our work in ref. ⁴¹, which distinguishes between the \(\\) states and atom loss (with the exception of mid-circuit ancilla measurement and the data in Fig. 2 and Extended Data Fig. 4c). In this method, a state-dependent circularly polarized one-dimensional optical lattice is used to pin one of the two qubit states^40,81,82, and an AOD tweezer moves the other qubit state a few micrometres away⁴¹, converting the atomic state to position that is then imaged via conventional polarization gradient cooling (PGC). The information about lost atoms does not allow us to correct the state but we can use it for error detection and postselection^42,43. In particular, for each observable, we use only the experimental shots where all qubits constituting that observable are present. Moreover, we can employ a sliding-scale postselection scheme where we additionally postselect on qubits being present within a given distance on the lattice (Extended Data Fig. 1b), which can mitigate the effects of error spreading throughout the circuit. To quantify this, we introduce a loss radius, which describes the distance on the honeycomb lattice within which the atoms must be present.

We use varying amounts of loss postselection for the different results in this work. Figure 2 has no loss postselection because we do not use state-selective readout for the data in that figure. In Fig. 3a, we use a loss radius of 0, and in Fig. 3c, we use a loss radius of 2 for all the string observables. In Fig. 4c,e, we use a loss radius of 0, and in Fig. 4f, we use a loss radius of 2 for all the exchange colour plots. Finally, for Fig. 5e,f, we use a loss radius of 2.

Here we briefly summarize the acceptance fraction for data throughout the paper, when using the loss and decoding postselection methods. We emphasize that this postselection is not critical to the main results of the paper, but rather we use this tool to improve the quality of results and elucidate the phenomena. In Fig. 2d, the acceptance fractions are directly plotted on the x axis (there is no additional overhead of loss detection because we do not use state-selective readout for this data). Similarly, for Fig. 2c, the acceptance fractions are plotted in Extended Data Fig. 4c for the different loops. For the string observables plotted in Fig. 3c, the acceptance fraction lies in the range of 3% to 25%. In Fig. 4c, the acceptance fraction is in the range of 65% to 86% (with higher acceptance for the shorter depths owing to less loss from gates), and for the data in Fig. 4c, it is 61%. In Fig. 4f, for the fermion exchange colour plots, it is in the range of 1% to 7% and in Fig. 4g, the acceptance fraction is shown on the x axis. Finally, for Fig. 5e, it ranges from 2% to 5% depending on the Floquet round, with all the points in Fig. 5f being 2%.

Floquet evolution circuits

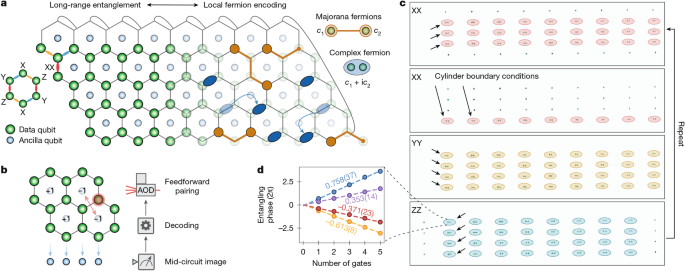
After the measurement-based state preparation, we keep one data-qubit sublattice in movable AOD traps (denoted by black circles in Extended Data Fig. 3), and at each time step, transport them next to the atoms in the even data-qubit sublattice to perform the tunable entangling gates. Global single-qubit rotations between entangling gates are used to change the basis between X, Y and Z. We perform dynamical decoupling throughout, including to cancel single-qubit dephasing from moves^6,9. During the Floquet evolution, we implement periodic cylindrical boundary conditions. In particular, owing to our array geometry, only the XX links couple the top row to the bottom row. For these links, we apply it in two steps, first moving the data qubits in AOD traps up one lattice site, and then moving the top row to perform gates with the bottom row (Fig. 1c). During this second step, the three other rows are moved out of the Rydberg beam to avoid extra gate errors. Conveniently, the structure for all the Floquet circuits in this work is the same (other than in Fig. 5), and so we only need to change the CPHASE gates between the different Floquet circuits. This enables the implementation of a wide variety of fermionic evolution with minimal experimental changes.

As the Floquet circuit commutes with closed-loop operators, the topological order is preserved as we evolve into phase B, up to a small decay from gate errors (Fig. 3b). In principle, the final state could be more fully characterized by measuring all closed-loop operators, including the additional larger loops measured in the initial state (Fig. 2b).

For the low-energy states of the Kitaev Hamiltonian in Fig. 3, we optimize the state-preparation circuits to maximize the overlap between bulk Majorana correlations (Extended Data Fig. 6a,b) of the prepared state and that of the Floquet ground state with Floquet time τ = 1/4J. We confirm that the resulting state has the correct Chern number and a similar energy to a state optimized purely based on energetic considerations. We note that the circuit depth of 6 is sufficient for this system size, but will necessarily increase for larger system sizes owing to the gap closing¹³. For the non-Abelian circuit, we used the CPHASE gates as shown in Fig. 3b, and for the Abelian II circuit, the circuit requires only 3 CPHASE gates: CP[−0.0625], CP[−0.0625] and CP[−0.3125]. The single-qubit sequence and atom motion is the same between all circuits in Fig. 3, with the exception of the final measurement basis rotations. The value of the plaquette parity at depth 0 is lower in Fig. 3b than in Fig. 2 owing to these additional errors.

For Fig. 4c, we use CP[−0.0625] gates to realize Jτ = 0.125, and for the case J_Z/J = 8, we use CP[0.5] gates for the J_Z term. For Figs. 4d and 5, we use CP[−0.0938] gates for the J_X and J_Y terms and CP[0.5] gates for the J_Z term to slightly increase the amount of hopping dynamics. We perform the measurements in Fig. 4e after depth 11 (it is noted that the final ZZ term for depth 12 commutes with the Z-basis measurement so we omit the final circuit layer).

Encoding fermions in qubits

The Hilbert space of N qubits and N fermions has the same dimension, but owing to non-local properties of fermions (anticommutation relations), mapping between them can be complicated. A direct translation on the operator level is given by the Jordan–Wigner transformation⁵, where for a particular site ordering, [1, …, N], we can identify complex-fermion creation and annihilation operators

and the corresponding Majorana operators

which can be directly checked to satisfy the canonical anticommutation relations, \(\a_i,a_j^\dagger \=\delta _ij\) and c_i, c_j = 2δ_ij. Beyond one dimension, this approach leads to macroscopic operator weight on the qubit side, even for simple local fermion operations such as nearest-neighbour hopping

for i < j (Extended Data Fig. 5a).

The idea of local fermion-to-qubit encodings⁷ relies on introducing a long-range entangled ‘background state’ |ø⟩ that is stabilized by the non-local operator strings, effectively cancelling them out. For example, if ∏_kZ_k in equation (4) is a stabilizer of |ø⟩, that is, (∏_kZ_k)|ø⟩ = |ø⟩, then the hopping term effectively becomes a simple weight-2 operator, c_ic_j ≈ X_iX_j. However, introducing these additional constraints on the state reduces the available Hilbert space for fermion degrees of freedom; thus, the system needs to be expanded by introducing additional data qubits. In the honeycomb encoding studied here, this manifests as the long-range entangled ZXXZ state on one sublattice being coupled to matter degrees of freedom through the parallel CY operation (Fig. 2a). In this setting, we have twice as many qubit degrees of freedom compared with fermionic ones, which grants enough space to enforce the stabilizer constraints.

We now show that the two-qubit interactions introduced in equation (1) correspond to hopping terms of Majorana fermions, c_j, localized at each site j. We begin by constructing Jordan–Wigner operators that are similar to those in equation (4) but modified to better suit our honeycomb lattice. We choose a site ordering starting in the top-left corner of the lattice and creating a continuous path \(\mathcalL\) through the entire system; for example, like the one in Extended Data Fig. 5a. We use a Jordan–Wigner operator⁸³

where \(\mathcalL_j\) is the sequence of links along path \(\mathcalL\) ending at site j, l(1/2) denotes the vertices of link l, and σ^(l) ∈ X, Y, Z is the Pauli operator along l. As the consecutive link operators always anticommute, the c_j operators defined this way satisfy the correct anticommutation relations and, as products of Paulis, are Hermitian and square to the identity operator. Now, if the hopping term is between two consecutive sites on path \(\mathcalL\), then we trivially recover \(\sigma _l(1)^(l)\sigma _l(2)^(l)\) as the rest of the string squares to identity. Finally, if the hopping term is between two nearest-neighbour sites that are not adjacent on \(\mathcalL\), we end up with

where \(\mathcalL_j\,\backslash \,\mathcalL_i\) is the ordered set of links between sites i and j along \(\mathcalL\). However, by applying the link (i, j), that path can be completed to a closed loop (on a cylinder it also needs to be multiplied by a conserved non-trivial loop around the cylinder), which, in turn, is exactly the product of all enclosed plaquette operators (Extended Data Fig. 5c). If the enclosed plaquettes are +1, the hopping term is effectively \(\sigma _i^(l)\sigma _j^(l)\), where l = (i, j). Thus, if all plaquettes are projected to be +1, such nearest-neighbour terms become the link operators and more general Majorana correlations are mapped to a Pauli string constructed from products of link operators. The plaquettes with −1 values act as \(\mathbbZ_2\) magnetic field fluxes, as they result in a π-phase for fermions hopping around them.

Complex fermions can always be formed by arbitrary pairing of Majoranas and here we choose to combine them along the ZZ links. Extended Data Fig. 5d shows how the hopping operator for such complex fermions can be realized through a linear combination of length-2 and length-4 Pauli strings, which symmetrically couple the different Majorana constituents. The operators of this form can be realized through Floquet engineering.

The two-qubit Pauli operators corresponding to the nearest-neighbour Majorana hopping, as derived here, constitute the exact interactions \(K_ij^\rmX\), \(K_ij^\rmY\) and \(K_ij^\rmZ\), implemented in this work. Moreover, the Hamiltonian given by nearest-neighbour Majorana hopping terms results in the original Kitaev honeycomb model³. In Extended Data Fig. 5e, we summarize all operators used in this work and explicitly write them out in both the qubit and fermion languages.

Free-fermion states and Hamiltonians

The Kitaev honeycomb model has an exact solution in terms of free fermions³, which enables efficient numerical simulation and benchmarking of most circuits in this work. Here we briefly summarize the main properties of such free-fermion states and Hamiltonians, focusing on Majorana operators, c_i, satisfying the canonical anticommutation relations c_i, c_j = 2δ_ij.

Free-fermion states are captured by the two-point correlation matrix Γ

with all higher-order terms decomposing into products of two-point functions via Wick’s formula⁸⁴.

A general quadratic Majorana Hamiltonian

is defined through a real, skew-symmetric matrix A^⊤ = −A, where matrix elements A_ij encode Majorana hopping between sites i and j. The correlations of the ground state are related to those of the Hamiltonian³, and a unitary evolution of an arbitrary free-fermion state Γ is given by

where \(\bfU(t)=\exp (-\bfAt)\) is a matrix describing the time-evolution of the two-point correlation matrix⁸⁵.

We focus on a translationally invariant system, which can be described by the unit-cell position R, and a label for the site within that unit cell, λ. For the honeycomb lattice, the unit cell has two sites, λ = e, o, corresponding to the even and odd sublattices, respectively, and equation (6) may be re-written as

where r is the relative position between the two relevant unit cells. In terms of momentum modes, c_k ∝ ∑_xe^−ik⋅xc_x, where x is the position operator, the Hamiltonian takes the form H = ∑_kH_k

where Δ and ξ functions are the Fourier transforms of \(A_\bfr^(e,e)\) and \(A_\bfr^(e,o)\), respectively. The Hamiltonian H contains two energy bands with dispersions \(\pm \varepsilon _k\propto \sqrt\xi _\bfk^2+\varDelta _\bfk^2\). In the original Kitaev model, the gap closes in phase B³, Δ_k = 0, but our effective Floquet Hamiltonians have a spectral gap owing to natural breaking of the time-reversal symmetry¹³. Knowing the numerical values of the Δ_k,ξ_k functions on a grid of points in the Brillouin zone enables evaluation of various band properties. In particular, evaluation of the Chern number requires only a few points in momentum space⁸⁶.  

Chern number

The gapped non-Abelian phase B of the Kitaev honeycomb model is characterized by a non-zero Chern number^14,87 of the excitation band. An odd Chern number guarantees that a magnetic flux is accompanied by an unpaired Majorana zero mode with non-Abelian (Ising anyon) statistics^3,15,88. In Fig. 3, we prepare a vortex-free ground state whose free-fermion parent Hamiltonian has a band with an odd Chern number. In principle, the Majorana zero modes could be prepared and probed directly, but the required circuit depths are larger than those used in this work¹³.

The Chern number is a topological invariant of the energy band, which characterizes the geometry of the single-particle eigenstates of H_k (refs. ^14,45). Those eigenstates, satisfying \(H_\bfk| n_\bfk\rangle =E_n,\bfk| n_\bfk\rangle \) for energy E, are defined up to an overall choice of phase gauge

where ϕ_k is the gauge parameter. To probe the local geometry of these eigenstates, as the momentum k is varied, we define the Berry potential (connection)

where \(\nabla _\bfk=(\partial _k_x,\partial _k_y)\) is the gradient in momentum space. The Berry potential is not gauge invariant, as it transforms as A_n,k → A_n,k − i∇_kϕ_k under equation (10), but the Berry curvature¹⁴

is invariant under equation (10) because ∇ × (∇ϕ) = 0.

The Chern number of the nth band is the integral of the Berry curvature over the first Brillouin zone

and is guaranteed to be an integer⁸⁹. Throughout this work we focus on the lowest energy band and omit the subscript n. For a given Bloch Hamiltonian in momentum space, H_k, the Chern number can be evaluated either by direct numerical integration of equation (13) or with a specialized numerical algorithm⁸⁶. Therefore, the task at hand is reduced to learning the momentum-space parent Hamiltonians of the states prepared in our experiments^90,91,92.

The free-fermion states are defined by their two-point correlation functions and, similarly, the free-fermion ground states are related to the single-particle eigenstates of the parent Hamiltonian³. We measure the open Pauli strings corresponding to the two-point Majorana correlations (Fig. 3c), and average their values over the bulk region (Extended Data Fig. 6a). We include all strings that span the bulk of the system, as depicted in Extended Data Fig. 6b, and effectively recover all the A_r matrix elements of the parent Hamiltonian (up to the norm) with r_x, r_y ∈ [−1, 0, 1] owing to the finite-size restrictions (Extended Data Fig. 6c). We then Fourier-transform these correlations onto a regular 5 × 5 grid in momentum space, resulting in an estimate of the parent Hamiltonian H = ∑H_k up to an energy scale ϵ_k.

Finally, we apply the algorithm of ref. ⁸⁶ to evaluate the Chern number. We diagonalize the H_k Hamiltonians at each k and calculate the phases of eigenstate overlaps between neighbouring momentum points and collect them in a tensor \(U_\bfk^\mu \), where \(\mu \in \\widehatx,\widehaty\\) denotes the direction in momentum space, which depends on only the eigenstates of H_k and not ϵ_k. Then, we calculate the discretized Berry curvature in equation (12) (Extended Data Fig. 6d) and sum its matrix elements to obtain the Chern number, which is guaranteed to be an integer⁸⁶. An interesting future effort would be to compare this approach with other methods for extracting the Chern number, such as the real-space formula of ref. ³.

The Chern number is obtained from the learned Hamiltonian and cannot be evaluated on individual snapshot data. When applying this procedure with the mean values plotted in the string distributions in Fig. 3c, we obtain C = 0 for the Abelian phase and C = 1 for phase B. To study the robustness of this result and the effect of postselection, we bootstrap the data⁹³ by evaluating the Chern number on Hamiltonians learned from randomized subsets (with replacement) of the entire dataset. The averaged Chern number approaches 1 as the batch size grows, and is reduced for small batches owing to projection noise (Extended Data Fig. 6f). For a batch size above 200, which is still a small fraction of our available data, the averaged Chern number is above 0.9 and quickly approaches 1 with increasing batch size. In that intermediate regime, postselecting on loss leads to a small but noticeable increase in the averaged Chern number (Extended Data Fig. 6g). These observations provide further evidence that the Chern number of our output distribution is consistent with having the value of 1.

We further study such Chern number evaluated on a noisy ensemble through numerical simulations, with the same approach as that used to calculate the string distribution in Fig. 3c. In Extended Data Fig. 6h, we evaluate the Chern number on string distributions simulated for various initialization and per-layer errors. We find that our parameters are comfortably within the regime of the unit Chern number.

Numerical simulations with errors

We perform circuit-level noisy numerical simulations for both the initial state-preparation step and the subsequent Floquet dynamics. The state-preparation circuit consists of Clifford operations only, and we simulate it using the stim package⁹⁴. The following Floquet circuit has non-Clifford operations but the effective free-fermion dynamics enable efficient simulation by keeping track of the correlation matrix in equation (5) through unitary dynamics, as described in equation (7).

We incorporate the effect of errors to the numerical simulation of free-fermion systems in a stochastic fashion, with an error channel with strength p_l applied after each circuit layer and the result averaged over many noise realizations. The coherent errors simply modify the phase of applied gates. The lost qubits are kept track of in a separate data structure and all subsequent gates that include those qubits are removed (with the error model still applied). When evaluating the observables, we postselect the data such that all qubits of the target observable are present (as is done in the experiment). The stochastic single-site Paulis are also kept track of in a dedicated data structure, and they flip the sign of all the following XX-, YY- and ZZ-link operators that they anticommute with. At the end of the circuit, the final set of Pauli errors is propagated through the observables being evaluated and flips them accordingly. The dynamics of interacting fermions are simulated with the approximate fermionic Gaussian-state approach⁸⁵.

We use a simple ansatz for our noise per gate layer, which consists of single-qubit incoherent Pauli errors and atom loss, and tune the overall noise strength to match select observables and use those fixed values for the majority of simulations. This phenomenological approach is not directly connected to any particular fidelity, as it models (in a naive way) all experimental contributions. As the state-preparation circuit cannot be simulated within the free-fermion framework, we initialize the noisy Floquet simulation with a layer of noise whose strength is chosen to match our experimental plaquette data in Fig. 2b, which gives the single-qubit initialization error of p_ini = 0.1. Similarly, the effective noise per gate layer was calibrated by applying isotropic fermion evolution (θ = 1) and looking at the ZZ-link observables at depth 12, resulting in the fitted single-qubit error per circuit layer p_l = 0.01. These error rates are divided between atom loss and (unbiased) single-qubit Pauli noise, with the loss constituting approximately 6% and 40% of p_ini and p_l, respectively. The simulations of circuits with interacting fermions assume perfect gate operations and include initialization errors calibrated to match the initial value in Fig. 5e. In general, for the fermion simulations (Figs. 4 and 5), we found that the dominant effect of noise was an overall rescaling of quantities rather than a large change in qualitative trends.

Emergent particle number conservation

In the quench experiment summarized in Fig. 4a–c, increasing J_Z/J leads to emergent particle number conservation at certain time intervals (depths 6 and 12). Here we describe this process in more detail and provide basic derivations of the effective Floquet Hamiltonians. The Floquet unitary for a single cycle of the quench experiment is

where the \(K_ij^\rmX/Y/Z\) interactions are defined in equation (1) and ⟨i, j⟩_X/Y/Z are the XX, YY and ZZ links, respectively. The \(K_ij^\rmZ\) term is, in terms of complex-fermion operators

where N_tot is the total particle number operator. Thus, for large J_Z values, there is a strong term in the Hamiltonian proportional to the total particle number. As the initial state is an eigenstate of N_tot, the subsequent evolution is projected into the subspace of N_tot with the same eigenvalue, which can be understood as orthogonal wavefunction components averaging out owing to fast oscillations at the timescale of 1/J_Z, effectively preserving the particle number and realizing complex-fermion dynamics. In Floquet evolution, we need at least 2 applications of U_F for the hopping along XX and YY to be affected by the N_tot operator and, thus, the shortest particle-conserving Floquet circuit is depth 6, as seen in Fig. 4c.

Such intuition can be further substantiated through analytical arguments on the operator level. As we show below, large-angle ZZ(θ) rotations effectively grow the nearest-neighbour link operators to length-4 strings in a way that can realize complex-fermion hopping (Extended Data Fig. 5d,e). The effect of varying J_Z can be understood by looking at a composite two-site unitary

where θ is proportional to J_Z and the remaining ZZ(2θ) can, in principle, be removed by setting θ → −θ in one of the two initial ZZ(θ)s. This operation can be understood as a ZZ(θ) unitary growing the X operator into a Y ⊗ Z one, and similar relations hold for all basis combinations. Moreover, equation (16) governs the growth of general strings, as X can denote a particular site on a larger string operator. The special case of θ = 1, corresponding to the CZ gate, results in a complete propagation.

Consider a hopping operator in a single direction, for example, along an XX link. In particular, take four qubits, labelled 1, 2, 3 and 4, arranged such that the pairs (1, 2) and (3, 4) form ZZ links and qubits (2, 3) are connected by an XX link. After applying two cycles of U_F (with discarded YY terms), we can instead interpret it as the first hopping along XX followed by the second one that is propagated according to equation (16). In the average Hamiltonian, for large angle θ, this effectively realizes a X₂X₃ + Z₁Y₂Y₃Z₄ operator, which corresponds to complex-fermion dynamics (Extended Data Fig. 5e). It is noted that X₂X₃ and Z₁Y₂Y₃Z₄ commute so there are no Trotter errors, but, in principle, there can be additional terms from other sites. In Extended Data Fig. 7b, we numerically evaluate the particle conservation of the effective depth-6 Hamiltonian (without the 2θ term in equation (16)) and see that indeed the particle creation is suppressed most when ZZ(θ) realizes a CZ gate.

Fermion hopping and density–density correlations

In our quench experiments with fermionic Hamiltonians, we study the time dynamics of two initialized particles (Fig. 4). Although the density of complex fermions at each step (Extended Data Fig. 7a) can reveal many spatial features, transport properties need to be inferred from other observables. For example, we could measure longer Pauli strings that include hopping terms (Extended Data Fig. 5e). Alternatively, density–density correlations

can also capture transport behaviour. Intuitively, if a particle starts at site A and moves to site B, the density at sites A and B should be anticorrelated owing to the particle leaving site A to appear at B. In Fig. 4e, we plot a horizontal cut of G_ij/⟨n_i⟩, which is additionally normalized by the density of the reference site i, and in Extended Data Fig. 7b, we present it for a two-dimensional neighbourhood of the reference site.

Furthermore, for free-fermion states, we can show that the connected density–density correlations in equation (17) directly capture hopping strength. After expanding the density operators, \(n_i=a_i^\dagger a_i\), the correlation function becomes

in terms of complex-fermion operators. For free-fermion states, the four-body term can be further decomposed into two-body terms through Wick’s theorem⁸⁴

where the last term vanishes when the particle number is conserved. This gives the expression for connected density–density correlations

which contains the negative magnitude of the hopping current and a positive contribution from pair creation. Thus, for free-fermion states with well-defined particle number, such correlations should be negative, with a magnitude proportional to squared hopping strength.

Fermion exchange protocol

Here we describe elements of the fermion exchange experiment presented in Fig. 4f. These experiments focus on four complex-fermion sites embedded in the full experimental array, as depicted in Extended Data Fig. 8a. To perform exact evolution without disturbing the rest of the system, we perform local gates by moving a subset of the atoms not involved in the exchange protocol to the storage zone. With this method, we can conveniently perform the required local gates without disturbing other atoms with either the Rydberg excitation or moving AOD traps.

The full sequence for the fermion exchange protocol is shown in Extended Data Fig. 8b,c. In the first step, we use a sequence of three two-qubit unitaries to realize the three-body interaction term R which creates the superposition of zero and two fermions at sites A and D. Then, we apply two different hopping steps, along YY and XX links (Extended Data Fig. 5d,e). As the Majorana hopping terms along XX and YY links do not conserve the particle number, we realize particle-conserving hopping through a sequence of four parallel two-qubit gate operations (Extended Data Fig. 8b,c). Finally, we apply R a second time to read out the exchange phase. In the absence of hopping, this final gate would complete the creation of two fermions at sites A and D, but owing to the −1 exchange phase, we expect zero fermions in the final image (if no errors are present).

We benchmark our ability to realize particle-conserving complex-fermion hopping terms by deterministically creating either 0 or 2 fermions, as shown in Extended Data Fig. 8d. To create two fermions, here we apply R twice in a row (an alternative method to the local single-qubit gates used in Fig. 4a, which also benchmarks our R unitary). We observe that applying the hopping unitary preserves the vacuum state and hops the two fermions at sites A and D to sites B and C, as expected. The results for both the full exchange and the control protocols match expectations and improve with postselection, providing evidence for observation of the exchange phase. A more robust protocol could involve measuring the full Ramsey fringe, for example, by applying a variable phase to the two-fermion basis state before the final partial-creation operator. Extended Data Fig. 8e shows data for the full exchange experiment, including some of the intermediate steps not shown in Fig. 4f.

Fermi–Hubbard implementation

Here we provide more information about the implementation of Fermi–Hubbard quantum simulations in Fig. 5. To prepare the initial chequerboard configuration, we apply local gates on 16 of the sites after state preparation (Extended Data Fig. 9a). For this circuit, we start with all operators on ZZ links with −1 value (by flipping the state of one of the data-qubit sublattices after the CY operation). Then we use local Raman gates to flip the required ZZ operators to prepare the correct pattern of localized fermions. Here we use local single-qubit Z gates and convert them to local X and Y gates using global π/2 Raman pulses. These local gates also flip four columns of plaquettes, which we pre-compensate for by flipping ancilla measurement results in the decoder.

We decompose each Floquet step of our simulations into (1) fermion hopping within each half and (2) coupling between the two halves to realize the spin interaction term. For independent hopping within each half of the system, we turn off the gates along XX and YY links connecting the two halves by modifying the atom motion pattern (Extended Data Fig. 9b). The spin interaction gates commute with the final measurement Z basis, so, for the data in Fig. 5e,f, we omit the final interaction step (for example, after the first Floquet round both circuits are exactly the same data).

Concretely, through the entangling operations between the two halves, we realize contact fermion interactions with four-body terms (Z_↑Z_↑) × (Z_↓Z_↓) across the two halves. In terms of Majorana operators, these terms are proportional to \((\rmic_ic_i^\prime )_\uparrow (\rmic_ic_i^\prime )_\downarrow \); in terms of complex fermions, they are of the form 4n_↓n_↑ − 2n_↓ − 2n_↑. The first-order Floquet Hamiltonian is therefore given by

which reproduces the usual Fermi–Hubbard model, equation (2), when the complex-fermion particle number is conserved.