Parent-of-origin effects on complex traits in up to 236,781 individuals

UK Biobank genotype processing

We used the UK Biobank Axiom Array data provided in PLINK format³⁹ and converted it to variant call format (VCF) using PLINK (v1.90b5)⁴⁰. We then used the UK Biobank SNPs quality control file (UK Biobank resource 1955) to filter the data using BCFtools (v1.8) to keep only variants used for the official phasing of the original UK Biobank data release³⁹, resulting in 670,741 variant sites across the 22 autosomes and 16,601 variant sites on the X chromosome. We then used the SHAPEIT5 phase_common tool¹¹ with default parameters and no filter on allele frequency to perform an initial phasing of autosomes. For the X chromosome, we proceed as described in the official phasing report of the UK Biobank whole-genome sequencing (WGS) data, interim release of 200,031 samples⁴¹. In brief, we removed pseudoautosomal regions, identified male individuals as genetically determined, forced reference allele homozygosity at heterozygotes sites in male individuals, and finally we provided the list of male individuals as input in the –haploid option of SHAPEIT5. Female individuals were phased as autosomes.

Close relative clustering

We use pairwise kinship estimates computed using the KING software (v2.2.4)⁴² to identify related individuals up to the fourth degree in the UK Biobank cohort. We identified parent–offspring duos and trios as having kinship between 0.1767 and 0.3535, IBS0 (proportion of SNPs with zero identity by state) below 0.0012 and age difference greater than 15 years^4,39, resulting in 1,071 trios and 4,136 duos (Supplementary Fig. 1a,b). We used Mendel error rate to ensure the accuracy of the identified parent–offspring trios (Supplementary Fig. 1c).

We next identified sibling pairs as those with kinship between 0.1767 and 0.3535, IBS0 above 0.0012 and age difference smaller than 15 years⁴, resulting in 22,751 pairs for 41,661 unique individuals (Supplementary Fig. 1a,b).

For individuals with more distant relatives (up to the fourth degree), we utilized a clustering approach to segregate relatives by parental sides using the igraph package in R⁴³, as previously done⁴. Through this method, we identified 274,525 UK Biobank participants whose relatives could be clustered into parental groups on the basis of their relatedness (Supplementary Fig. 1d). In our analysis, we refer to those close relatives as surrogate parents.

We finally identified individuals who have both available parental genomes and inferred surrogate parents, and thus can be used for validating our method. This allowed us to perform the entire analysis using surrogate parents and excluding parental genomes, effectively simulating the remaining individuals without available parental genomes, and later reintroduced the parental genomes solely for validation and accuracy estimation. In subsequent sections, we refer to those as the validation cohort. A total of 2,141 individuals met these criteria, resulting in 3,160 target–relative pairs (Supplementary Fig. 2a). For each target–relative pair, we used KING pairwise kinship estimates between the relative of the target and the parents of the target to assign the relative to a parental side (Supplementary Fig. 2b). This validation cohort was subsequently used to assess the accuracy of our inferences and to derive probabilities for PofO assignments.

Interchromosomal phasing from available parental genomes

For individuals with available parental genomes (1,071 trios and 4,136 duos), we performed interchromosomal phasing using the –pedigree option of SHAPEIT5 (ref. ¹¹). This method requires a three-column pedigree file listing offspring, fathers and mothers. In cases in which one parent was unavailable, the missing parent was indicated by ‘NA’. This procedure resulted in phased genotype data (that is, haplotypes). The order of the haplotypes corresponded to the order of parents in the pedigree file (here, first haplotypes were paternally inherited, and second haplotypes were maternally inherited). Consequently, this method allowed for direct inference of the PofO of haplotypes from statistical phasing when parental genomes were available. The key advantage of using pedigree-based statistical phasing over traditional Mendelian logic is its ability to infer the PofO of alleles even when both parents are heterozygous. This is accomplished by statistical phasing, leveraging haplotype information from the broader population, leading to more accurate results. In this study, the PofO inferred from parental genomes serves as the ground truth. This ground truth is critical for validating the accuracy of PofO inference derived from surrogate parents in the validation cohort (see subsequent sections).

Interchromosomal phasing from surrogate parents

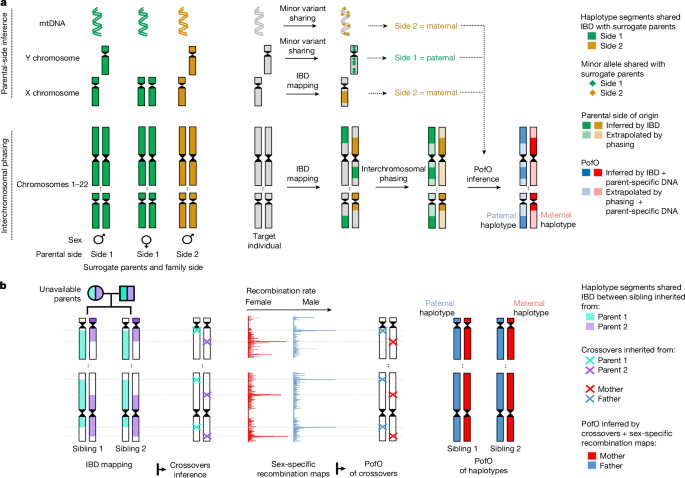
IBD mapping is a powerful approach for identifying haplotype segments co-inherited from a common ancestor among pairs of relatives. By analysing haplotype segments’ shared IBD with the same set of surrogate parents across the 22 autosomes for a given target individual, we could determine which haplotype segments were inherited from the same parent. This enabled the construction of partial parental haplotype sets, which could then be used to perform interchromosomal phasing that segregates haplotypes inherited from each parent across the genome. This approach goes beyond traditional phasing methods, which are limited to resolving haplotypes within individual chromosomes (intrachromosomal phasing). For 274,525 individuals with identified surrogate parents, we used the THORIN tool⁴ to map haplotype segments’ shared IBD between the target individuals and their surrogate parents. These IBD-shared segments served as the foundation for both intrachromosomal and interchromosomal phasing, building on previous methodologies⁴. The key principle here is that haplotypes’ shared IBD with the same surrogate parents originate from the same parent. Consequently, these haplotypes should consistently appear on the same parental haplotype across autosomes. In practice, we filtered for shared haplotype segments longer than 3 centimorgans (cM), which we incorporated into a scaffold file. This scaffold was then used as input for the SHAPEIT5 phase_common tool. This step allowed us to refine and re-estimate haplotypes from genotype data, while simultaneously correcting intrachromosomal phasing switch errors and performing interchromosomal phasing by assigning all haplotypes shared with the same surrogate parents to the same parental haplotype (for example, first or second) across all 22 autosomes.

Parental side determination of surrogate parents

X chromosome

IBD mapping on the X chromosome has been shown as an accurate approach to identify maternal relatives for male target individuals⁴. Here we built on this previous approach to probabilistically infer the parental side of close relatives. To do so, we utilized the THORIN tool to map IBD segments between a target individual and its surrogate parents. When a target individual has several surrogate parents from the same family side, we combined them into a single surrogate parent set, which allowed the THORIN tool to merge overlapping IBD segments from different relatives within the same set. We then retained only the largest IBD segment (size computed in Morgans) between the target and each surrogate parent set. Unlike the previous approach that only determine maternal relationships using a strict threshold in the X chromosome IBD⁴, we probabilistically determined the parental side of surrogate parents. To derive probabilities of a surrogate parents set being on the paternal or maternal side, we used the validation cohort and computed the length of the X chromosome IBD haplotype segment shared with the target individual. This method effectively maximizes the number of surrogate parents with determined parental status.

Let \(l(i,j)\) mark the length in cM of the longest haplotype segment shared on the X chromosome between individuals \(i\) and \(j\). Let \(I_\rmpat(i)\) refer to the set of all \(N_\rmpat(i)\) paternal relatives of individual \(i\) and similarly for \(I_\rmmat(i)\) and its cardinality \(N_\rmmat(i)\). In addition, we define \(l_\rmpat(i):=\frac1N_\rmpat(i)\cdot \sum _j\in I_\rmpat(i)l(i,j)\) as the (average) length of X chromosome haplotype sharing of an individual \(i\) with its surrogate fathers, in the training set. We define \(l_\rmmat(i)\) analogously for surrogate mothers. As we know that surrogate fathers should not share an X chromosome segment and surrogate mothers are much more likely to share longer segments, we expect \(l_\rmmat(i)\) to be much larger than \(l_\rmpat(i)\).

Finally, let \(I_\rmpat\) refer to the set of \(N_\rmpat\) target individuals that have paternal relatives in the training set. In the same way, \(I_\rmmat\) refer to the set of \(N_\rmmat\) target individuals that have paternal relatives in the training set.

For any fixed length \(l\), let us define the proportion of an event of two individuals sharing X chromosome haplotypes of length shorter than \(l\) when one individual is a paternal relative of the other one:

where \(I(A)\) takes the value of 1 if statement \(A\) is true and zero otherwise. When a shared segment length is very large, the proportion is expected to be very small, that is, it is unlikely to share large segments with surrogate fathers. Analogously, we can define

As,

and

and they sum up to 1, that is,

Assuming a uniform prior, that is, \(Pr(j\in I_\rmpat(i))=Pr(j\in I_\rmmat(i))\), we have

Thus,

We can similarly derive that

Note that when \(l\) is large \(\frac1N_\rmmat\sum _i\in I_\rmmatI(l_\rmmat(i) > l)\) will dominate and hence the ratio will approach 1. Hence, when \(l\) is large, it is a faithful measure of the probability that if we observed \(l\) long X chromosome sharing between two individuals (\(i\) and \(j\)), how likely it is that \(j\) is on the maternal side of \(i\). However, as \(l\) decreases, it does not inform us about the chances of \(j\) being on the maternal side of \(i\).

In theory, we could have used \(\hatPr(j\in I_\rmpat(i)| l(i,j)=l)\) and \(\hatPr(j\in I_\rmmat(i)| l(i,j)=l)\), but in practice, these measures turned out to be too noisy when not enough \((i,j)\) training data pairs were available with \(l(i,j)\) being close enough to \(l\).

We initially applied this approach to the male individuals of the validation cohort (n = 857). We found that haplotype segments’ shared IBD with surrogate fathers are all shorter than 11.3 cM, and 99% of them are shorter than 3 cM (Supplementary Fig. 6a). We then evaluated the accuracy of our probabilistic assignment. To do so, we proceeded with a ‘leave one sample out’ approach: we removed a given individual from the training set and predicted its paternal and maternal sides by deriving probabilities using the N − 1 individuals of the training set (Supplementary Fig. 6b). We repeated this for the N individuals of the training set. To compute accuracy at a given maternal probability P, we defined true positives as the number of surrogate mothers with probability >P, and false positives as the number of surrogate fathers with probability >P. We then computed accuracy as TP/(TP + FP) (Supplementary Fig. 6c).

Applying this method to the UK Biobank male individuals with available surrogate parents and unknown parental assignment, we were able to probabilistically assign parental sides to surrogate parents for a total of 115,027 male individuals. Of note, 34% of these individuals (n = 39,100) achieved a parental assignment probability of 1, indicating a robust and reliable classification (Supplementary Fig. 6d).

mtDNA

mtDNA, which is inherited exclusively from the mother, serves as a valuable tool for identifying maternal relatives. However, the UK Biobank Axiom array data proved inadequate for this purpose due to the limited number of genotyped variants (n = 265). To overcome this limitation, we used the WGS GraphTyper cram file available on the UK Biobank Research and Analysis Platform for 500,000 individuals. We called variants from the mtDNA WGS cram files for 274,525 UK Biobank individuals (those with interchromosomal phasing) and their surrogate parents using the MitoHPC software⁴⁴ with default parameters. We then aimed to determine the parental side of each surrogate parent on the basis of genetic similarities of their mtDNA. However, most IBD mapping software relies on the Li and Stephens hidden Markov model, which models the human recombinant genome. Owing to the lack of recombination of mtDNA and its higher mutation rate than autosomes, these kinds of software proved unsuitable. As a result, we adopted an alternative approach to evaluate non-recombinant DNA sharing between pairs of individuals. This approach, inspired by the Jaccard index, introduces the term minor variant sharing (MVS), which captures the proportion of shared minor alleles between relative pairs. The approach overcomes the limitations of traditional IBD mapping for mtDNA by replacing IBD with identity by state (IBS).

Let \(V_t\) denote the vector of genotypes for the \(M\) mtDNA variants in the target individual, and \(V_r\) the corresponding vector for the relative of the target. In both vectors, genotypes are coded as 0 for the major allele and 1 for the minor allele. Thus, we computed mtDNA MVS as:

Using the validation cohort, we found that maternal relatives exhibit a higher average MVS than paternal relatives (Supplementary Figs. 7–9a). The effectiveness of this metric depends on the degree of relatedness and is particularly precise for second-degree relatives. For these relatives, MVS values strongly correlate with the probability of the surrogate parent being on the maternal side. However, for more distant relatives (due to the possible presence of an intermediary male relative in the genetic lineage disrupting mtDNA inheritance), low MVS values do not translate to paternal relationship.

To predict the parental side of relatives from the mtDNA MVS, we adopted a perfectly analogous procedure to the one outlined for chrX sharing whereby we replaced chrX IBD segment length with the mtDNA MVS value. To evaluate the accuracy of this approach, we stratified target samples by their degree of relatedness to their closest relatives in the cohort (Supplementary Figs. 7–9C).

This methodology was applied to predict the relative parental side for 19,022 second-degree, 114,965 third-degree and 312,447 fourth-degree target–relative pairs (Supplementary Figs. 7d–9d). For targets with multiple relatives of the same degree, we retained only the relative with the highest predicted accuracy, resulting in 17,625 second-degree, 95,151 third-degree and 204,924 fourth-degree target–relative pairs. Of note, 69,580 of these pairs were assigned to a parental side with a probability greater than 0.99 (Supplementary Fig. 10a). In addition, parental side assignments were supported by multiple relatives for 9,948 individuals (Supplementary Fig. 10b).

PofO determination

From close relatives

We integrated interchromosomal phasing with inferred parental side information from relatives to determine the PofO for each parental haplotype set. Specifically, a haplotype set was classified as maternally inherited if its haplotypes shared IBD segments with maternal relatives, and as paternally inherited if they shared IBD segments with paternal relatives. When the assignment was possible for only one of the two haplotypes in a target individual, we assumed the absence of uniparental disomy and inferred the parental origin of the second haplotype by exclusion.

From crossovers to PofO inference in siblings

By analysing IBD segments shared by siblings, we can infer crossover locations in parental haplotypes. Together with sex-specific genetic recombination maps⁹, Qiao et al.¹⁰ have demonstrated that we can estimate the likelihood of a set of crossovers originating from either the mother or the father, allowing us to determine the PofO of the haplotype carrying this set of crossovers. This method is reliable exclusively for sibling pairs, as they guarantee that the detected crossover events occurred in the parents. We identified IBD-shared haplotypes between sibling pairs using the THORIN tool and kept only segments larger than 3 cM. We used IBD segment breakends as crossover positions. However, we were very unlikely to capture the exact crossover positions using this approach. First, because we were restricted to genotyped markers. Second, owing to the nature of the Li and Stephens hidden Markov model used to map IBD segments in the THORIN tool, which does not transition at homozygous sites, we identified crossovers at heterozygotes only. Therefore, we used a 1,000-bp window around each crossover position to increase chances of including the true position. We then used recombination maps to extrapolate the probability of a crossover occurring within this window on the basis of the genetic distance in Morgans between the start and end positions of the window. We repeated this process for both the male-specific and the female-specific recombination maps for all the crossover events identified on the same haplotype.

Let \(D_f(p)\) be the distance in Morgan of the 1,000-bp window around the crossover inferred at position p, originating from the female-specific recombination map, and \(D_m(p)\) the distance originating from the male-specific recombination map position. To determine the most likely parent giving rise to an observed crossover at position p, we can compute the difference on log(Morgan) scale between male and female recombination probability:

Assuming perfect intrachromosomal phasing, we can deduce that all crossovers identified on a given haplotype are inherited from the same parent. We can therefore aggregate Morgan differences for the n₀ and n₁ crossover positions of haplotype 0 and haplotype 1 on chromosome c, respectively. Let us define a score (S) for chromosome c using both haplotypes as:

This approach can be sensitive to misidentified crossovers, which may arise from various sources, such as inaccuracies in IBD segment boundaries due to errors in the IBD mapper, genotyping errors or consanguinity. These errors can inflate or deflate the global score. To mitigate this and remove confounders, we compared the observed number of crossover N_obs(CO) events to the expected number N_exp(CO). N_exp(CO) depends on the chromosome length in Morgan \(\rml_\rmc\). As we aggregated crossovers across both siblings first and second haplotypes, the expected number of crossovers N_exp(CO) on these four haplotypes follows a Poisson distribution with \(\lambda =4\rml_\rmc\). However, given that the observed number of crossovers N_obs(CO) inferred using our approach depends on IBD sharing patterns, N_obs(CO) can range from zero when siblings are in IBD2 or IBD0 for the entire chromosome, to \(4\rml_\rmc\). However, artefacts from the IBD mapper can inflate this number. Therefore, we evaluated the distribution of observed crossover for each chromosome, and individuals strongly deviating from this distribution (more than 10 times the interquartile range) were removed.

The accuracy of determining the PofO of haplotypes depends on the number of crossovers analysed, which varies with chromosome length (in Morgans; Supplementary Fig. 11a). Using intrachromosomal phasing, we could only determine the PofO for crossovers within individual chromosomes by computing \(S_c\), requiring separate calculations for each chromosome. By contrast, interchromosomal phasing enabled us to group crossovers occurring across the entire genome on the same parental haplotype set, allowing us to infer the PofO for the entire set at once, where the final score (S) was simply adding up the scores across chromosomes (Supplementary Fig. 11b):

We initially assigned the PofO of haplotype using this score as follows: a negative score means that the first haplotype of the individual is paternally inherited, and a positive score means that it is maternally inherited. We evaluated the efficiency of our approach using a subset of the validation cohort that included 88 individuals with at least one sibling and available interchromosomal phasing from close relatives. As interchromosomal phasing might not be available for all chromosomes, we simulated varying conditions by altering the number of chromosomes analysed per individual, resulting in different numbers of inferred crossovers depending on the genomic length analysed (Supplementary Fig. 11b). We found that interchromosomal phasing substantially increases accuracy compared with single chromosome analysis (Supplementary Fig. 11c–e). Moreover, the PofO of crossovers could be assigned for 96.4% of individuals using interchromosomal phasing versus only 51.3% with intrachromosomal phasing (Supplementary Fig. 11f).

To avoid relying on arbitrary thresholds, we utilized the validation cohort to derive probabilistic determinations of the parental origin of haplotypes using inferred crossovers from interchromosomally phased data. Let us consider a score \(S_t\) for the target individual \(t\) that has been computed using a specific number of interchromosomally phased chromosomes. Together, these chromosomes have a genomic length of \(l_t\). As the number of observed crossovers N_obs(CO) depends on \(l_t\) and that \(S_t\) depends on N_obs(CO), we define \(I_\rmpat(t)\) as the set of individuals of the validation cohort for which \(H_\) is paternally inherited and for which \(l\) is within the window \((l_t-3,l_t+3)\), and \(I_\rmmat(t)\) as the set of individuals of the validation cohort for which \(H_\) is maternally inherited and for which \(l\) is within the window \((l_t-3,l_t+3)\). The cardinality of these sets is denoted by N_pat(t) and N_mat(t), respectively. This allowed us to compare our obtained total score to the score obtained for a subset of the validation cohort that had a similar available genomic length as \(l_t\).

As negative scores are compatible with paternal assignment and positive scores with maternal assignment, we could then define the probability of paternal origin of a genome-wide haplotype set of target sample t as follows

and \(Pr_\rmmat(t)\) is defined as \(1-Pr_\rmpat(t)\).

We evaluated the accuracy of this approach using the validation cohort. To explore all dependencies, we simulated varying conditions by altering the number of chromosomes analysed per individual, ranging from only one chromosome used to the full set of interchromosomally phased chromosomes for each individual. As expected, we observed better accuracy for scores strongly deviating from zero (Supplementary Fig. 12a). In addition, we observed that larger available genomic lengths (that is, more chromosomes) resulted in less errors, and that no errors were detected when using more than 10 Morgan (Supplementary Fig. 12b). Of note, when using the full set of available interchromosomally phased chromosomes per individual in the validation cohort (that is, the most realistic scenario), we achieved 100% accuracy (Supplementary Fig. 12a,b).

We applied this approach on 26,635 individuals with available interchromosomal phasing and at least one sibling. The specific configurations of our sample set (genomic length and number of crossovers) matched the highest accuracy (Supplementary Fig. 12c,d).

As interchromosomal phasing is not available for all siblings, we additionally use 14,695 individuals without interchromosomal phasing available and at least one sibling. We applied the single-chromosome approach using strict threshold at scores of −2 and 2 to determine the PofO of each target haplotypes separately (see Supplementary Fig. 11 for accuracy), and assessed the different characteristics of this inference (Supplementary Fig. 13).

Accuracy of combined PofO predictors

We used our PofO predictors to attempt to assign the PofO for 272,384 individuals with interchromosomally phased data and unavailable parental genomes. Of these, 5,312 were filtered out due to sex chromosome aneuploidy, excess of X chromosome heterozygosity for male individuals, lack of mtDNA WGS data, or withdrawal of individual or relative in-between the beginning of the analysis and the use of the WGS data. For the 267,072 remaining individuals, we attempted to assign the PofO using our predictors. A given individual can have several predictors of its haplotype PofO: X chromosome IBD, mtDNA MVS from different relatives and sib-score. For each individual, we kept the predictor with the highest estimated accuracy to determine parental side. As a result, we could unambiguously determine the parental side of relatives for 99.1% of the target individuals (n = 264,597). For ambiguous cases (n = 2,475), we then prioritized predictors in the order indicated by overall accuracy of the predictor: X chromosome, sib-score and MVS for second-degree relatives. We obtained 209 individuals with parental sides undetermined because of conflicting mtDNA-based PofO predictions from different (third and fourth degree) relatives in the same surrogate parent cluster. In total, we successfully assigned the PofO for 266,863 individuals, and the PofO remained unassigned for 5,521 individuals that had available interchromosomal phasing (5,312 filtered out in the quality control and 209 with conflicting PofO predictors). In addition to assigning the PofO for individuals with available interchromosomally phased data, we also used single-chromosome sibling score for 14,596 individuals with at least one sibling and unavailable interchromosomally phased data, bringing our total number of individuals with PofO assigned from predictors to 281,459. Finally, we also added PofO prediction from available parental genomes for 1,071 trios and 4,136 duos, for a total of 286,666 individuals.

We compared our PofO determination to the one obtained from parental genomes at each heterozygous site of the validation cohort, revealing an accuracy of 97.94% (Supplementary Fig. 14).

Parental haplotypes imputation and encoding

To infer the PofO for untyped alleles, we used haploid imputation as previously done⁴ to separately impute each parental haplotype using the –out-ap-field option of IMPUTE5 (v1.2.1)⁴⁵ and the Haplotype Reference Consortium as a reference panel. This provides an AP field (alternative allele probabilities per haplotype), indicating imputed paternal and maternal allele dosages. We then kept only variants with an INFO score greater than 0.8 and minor allele frequency greater than 1%.

We encoded parental haplotype in separate files. For each target and at each variant, we weighted the parental allele imputed dosage with the parental assignment probability. Let us consider an imputed variant v for a target individual t with haploid imputed dosages \(AP_\rmmat(t,v)\) and \(AP_\rmpat(t,v)\) for maternal and paternal haplotype, respectively. Let us also consider the parental assignment probability P_t for the target t given by combined predictors. We re-encoded our data as:

From this, we adapted a haploid genotype posterior probability field GP (probability triplets for the three possible genotypes) as:

Finally, we also combined maternal and paternal alleles at heterozygous sites only to directly test for differential effect (all homozygous sites are encoded as missing):

where

The data were re-encoded as VCF files, which were then converted into PGEN files using PLINK (v2.00a4.3).

Identification of POEs

POEs is a generic term encompassing many types of POE. In this article, we claimed POE if the maternal and paternal effect estimates of an allele were significantly different. To detect these, we assessed the phenotypic difference between those heterozygous individuals who carry the effect allele paternally versus maternally. Once such a difference was detected, we further classified POEs on the basis of the size and direction of the paternal versus maternal effects (Supplementary Fig. 16).

Phenotype processing

We processed the 59 selected traits (Supplementary Table 1) as follows. For quantitative traits, we averaged out phenotype values across all available time points to obtain one value per individual. We then inverse-normal quantile transformed each trait using the rntransform function from the GENABEL R package⁴⁶. For T2D, we defined cases on the basis of the ICD-10 (International Classification of Diseases, Tenth Revision) code ‘E11’ (non-insulin-dependent diabetes mellitus). To enhance specificity, we excluded from the case and control groups any individuals who also had ICD-10 code ‘E10’ (insulin-dependent diabetes mellitus). Furthermore, individuals diagnosed with other forms of diabetes (for example, gestational diabetes) were removed from both cases and controls.

Association tests

To perform GWAS analysis, we used REGENIE (v3.2.9)³⁸. Only genotyped variants were used for model fitting, as recommended (that is, REGENIE step 1). We then tested paternal, maternal and differential haplotypes (that is, \(GP_\rmpat\), \(GP_\rmmat\) and \(GP_\rmdiff\)) separately (that is, REGENIE step 2). We denote the P values resulting from these GWAS \(P_P\), \(P_M\) and \(P_D\) for paternal, maternal and differential GWASs, respectively. We used the first 20 principal components, age and sex as covariates. In addition, we restricted our association tests to individuals who self-identified as ‘white British’ and have a similar genetic ancestry determined by principal component analysis (UK Biobank field 22006), and we restricted the differential scan to variants with imputed parental dosages greater than 0.99, as previously done⁴.

Given the complexity and diverse nature of POEs, we used a multi-purpose approach to identify novel putative associations. Besides the traditional genome-wide scan, we focused on known imprinted regions, that is, within a 500-kb window around known imprinted genes⁷, which are more likely to exhibit POEs. Second, we expanded our analysis to perform a GWAS scan focusing on regions exhibiting additive association with the examined trait. For these analyses, we selected a total of 59 phenotypes, including anthropometric traits, growth-related measures, cardiometabolic traits and blood biomarkers. This comprehensive approach allowed us to maximize the potential for discovering novel POE signals across a broad spectrum of traits. To account for the number of traits tested, we computed phenotypic correlation between each pair of traits. We then used the function simpleM from the R package hscovar to compute the effective number of traits tested, which resulted in \(N_\rmeff(\rmtraits)=48\). All associations were pruned using genetic distance smaller than 500 kb and linkage disequilibrium < 0.01.

To identify POE genome wide, we used a stringent POE significance threshold (that is, differential P value P_D) of 5 × 10⁻⁸/48 = 1 × 10⁻⁹ to correct for the number of independent tests performed across our 59 selected traits.

To identify POE within additive regions, we first selected significant additive associations (P < 5 × 10⁻⁸/48 = 1.04 × 10⁻⁹), which we then tested for POEs using the differential GWAS. We corrected our POE significance threshold for the number of identified additive association such that the differential P value P_D threshold = \(0.05/N_a\), where \(N_a\) is the number of independent additive associations.

To avoid overly conservative type I error control, we adjusted the POE significance threshold by accounting for the linkage disequilibrium structure within imprinted regions. After calculating the number of effective independent tests, we applied a significance threshold of \(P_D < 0.05/16,574=3.01\times 10^-6\), where 16,574 is the number of independent tests performed within imprinted regions. POEs identified at this threshold are referred to as suggestively significant POEs. In addition, we verified whether the identified associations would pass the more stringent threshold of 6.27 × 10⁻⁸, which corresponds to 3.01 × 10⁻⁶/48, where 48 is the effective number of traits tested. POEs identified at this threshold are referred to as significant POEs.

Classification of POEs

To classify POEs, we categorized associations on the basis of the relative magnitudes and directions of the maternal (Z_Mat) and paternal (Z_Pat) Z-scores. The classification criteria are as follows:

• Bipolar effects: the maternal and paternal effects are of opposite signs (\(\textsign(Z_\rmMat)\ne \textsign(Z_\rmPat)\)) and have similar magnitudes (\(| Z_\rmMat| > 0.5\times | Z_\rmPat| \) and \(| Z_\rmPat| > 0.5\times | Z_\rmMat| \)).

• Maternal effect: the maternal Z-score is at least twice as large as the paternal Z-score in absolute value (\(| Z_\rmPat| < 0.5\times | Z_\rmMat| \)).

• Maternal asymmetric: the maternal and paternal effects have the same sign, the maternal effect is dominant (\(| Z_\rmMat| > | Z_\rmPat| \)) but the paternal effect is still substantial (\(| Z_\rmPat| > 0.5\times | Z_\rmMat| \)).

• Paternal effect: the paternal Z-score is at least twice as large as the maternal Z-score in absolute value (\(| Z_\rmMat| < 0.5\times | Z_\rmPat| \)).

• Paternal asymmetric: the paternal and maternal effects have the same sign, the paternal effect is dominant (\(| Z_\rmPat| > | Z_\rmMat| \)), but the maternal effect remains notable (\(| Z_\rmMat| > 0.5\times | Z_\rmPat| \)).

Conditional POE analyses

To explore the presence of secondary, independent POEs near primary loci, we performed conditional analyses using REGENIE³⁸. This involved including the lead linkage disequilibrium-pruned variant as a covariate in the model to account for its effect, to obtain a conditional differential P value \(P_D_c\) for the remaining variants. By conditioning on the lead variant, we aimed to identify secondary POEs that might otherwise remain undetected due to linkage disequilibrium or proximity filtering. This approach ensures that any secondary signals are independent of the primary association.

Replication of known PofO associations

We used publicly available summary data for eight studies reporting POEs or separate paternal and maternal GWAS estimates^{4,5,7,12,13,14,15,16}. When differential GWAS coefficients were not directly available, we computed a differential scan similar to the one performed in our study:

where \(\Phi \) is the cumulative distribution function of the standard normal distribution and \(|Z_D|\) is the absolute value of the Z-score.

Sex-specific differences in POEs

We performed a differential GWAS scan separately for male and female individuals to obtain sex-specific coefficients. We then assessed significant differences of effects using a Z-score approach:

SNP heritability

We performed linkage disequilibrium score regression⁴⁷ to compute SNP heritability (h²) using our GWAS association summary statistics and publicly available linkage disequilibrium scores from the 1000 Genome Project. We showed that the linkage disequilibrium based on the parental dosage difference equals the linkage disequilibrium of additive genotype dosage (see Supplementary Note 21). We munged GWAS summary data and estimated heritability with default parameters. When h² was computed for subsets of the genome (that is, within and outside imprinted regions), we weighted the estimates by the proportion of variants included in the subset. To test the difference between heritability estimates, we combined estimates into a Z-score :

where \(a\) and \(b\) represent (1) differential estimates within imprinted regions and outside imprinted regions (Extended Data Fig. 7a), or (2) paternal and maternal estimates (Extended Data Fig. 7c,d).

Replication analyses with childhood and infant traits

Comparative traits at age 10 in the UK Biobank

In the UK Biobank, we tested comparative body height at age 10, comparative body size at age 10 and birth weight. For comparative height size at age 10 (phenotype code 1697), we encoded the data as shorter = 0, about average = 1, and taller = 2. For comparative body size at age 10 (phenotype code 1687), we encoded the data as thinner = 0, about average = 1, and plumper = 2. We treated these three traits as quantitative traits and inverse-normal quantile transformed each trait using the rntransform function from the GENABEL R package⁴⁶.

Infant height and BMI in MoBa

MoBa^23,48 is a prospective cohort study that recruited pregnant women in Norway between 1999 and 2008. The study enrolled approximately 114,500 children, 95,200 mothers and 75,000 fathers from 50 hospitals across Norway. Anthropometric measurements of children were collected at hospitals at birth and during routine visits at 6 weeks, 3 months, 6 months, 8 months, 1 year, 1.5 years, 2 years, 3 years, 5 years, 7 years and 8 years of age. Parents provided these measurements via questionnaires²³. Parental origin of alleles was inferred using parental genomes. Parent–offspring trios were excluded if they met any of the following criteria: stillborn, deceased, twins, missing data in the Norwegian Medical Birth Registry, missing anthropometric measurements at birth, pregnancies for which the mother did not respond to the first questionnaire, or missing parental DNA samples. Genotyping was performed on multiple sets of trios randomly selected from the study biobank, for a total of 45,402 offsprings with both parents genotyped and at least one BMI or height measurement available. We estimated POEs on infancy and childhood BMI and height at 11 time points (at 6 weeks, 3, 6 and 8 months, and 1, 1.5, 2, 3, 5, 7 and 8 years of age; Supplementary Table 8) using REGENIE and including genotyping batch effects for the child, mother and father, the first 10 principal components, and the sex of the child as covariates. Similarly to the UK Biobank and Estonian Biobank cohort, we tested parental alleles in the second step. We then estimated the differential coefficients by comparing paternal versus maternal coefficients using a Z-score approach. Depending on the time point, up to 42,346 individuals were included in the association analyses.

Multiple testing correction

We restricted this analysis to seven loci found to be associated with obesity-related traits, and three height-associated loci in the UK Biobank cohort. In the UK Biobank, we tested the three height-associated loci for association with comparative height size and the seven obesity-related loci for association with both comparative body size and birth weight, for a total of \(3\times 1+7\times 2=17\) tests.

In Moba, we tested the three height-associated loci for association with infant height and the seven obesity-related loci for association with infant BMI. As BMI and height measurements at different time points are correlated, we estimated the number of effective tests to apply appropriate multiple testing correction. This resulted in five independent measurements for both BMI and height, for a total of \(3\times 5+7\times 5=50\) independent tests.

In total, we set our significant threshold to \(0.05/(17+50)=7.4\times 10^-4\) when evaluating our original POEs for association with childhood traits.

Estonian Biobank genotype processing

We used the quality-controlled genotype data genome built GRCh38 in VCF provided by the Estonian Biobank team²⁵. Similar to when processing the UK Biobank data, we used SHAPEIT5 (ref. ¹¹) to phase autosomes and X chromosome, and KING⁴² to estimate relatedness. To impute the Estonian Biobank genotype data, we used the Estonian Biobank WGS reference panel⁴⁹, including 2,695 individuals. We performed phasing of the reference panel using the two-step process of SHAPEIT5 (ref. ¹¹). We used the resulting reference panel to impute the SNP array data using IMPUTE5 (ref. ⁴⁵). For all the remaining analysis, we proceed as for the UK Biobank. To infer the PofO of haplotypes for individuals without available parental genomes, we used only IBD sharing on the X chromosome and sibling score, as mtDNA WGS were not available to compute MVS. For replication analysis, we focused on traits with at least 20,000 individuals in the Estonian Biobank. This resulted in ten traits: standing height, glucose levels, T2D, HbA1c, HDL-C and triglyceride levels, hip circumference, creatinine and cystatin C levels, and platelet count. We derived phenotypes from electronic health records, unless NMR metabolomics measurements were available⁵⁰, which were available in a larger sample size than blood biomarkers (for glucose, triglyceride, HDL-C and creatinine levels). Depending on the phenotype, up to 85,050 individuals were included in the association analyses.

Ethics statement

The activities of the Estonian Biobank were regulated by the Human Genes Research Act, which was adopted in 2000 specifically for the operations of the Estonian Biobank. Individual-level data analysis in the Estonian Biobank was carried out under ethical approval 1.1-12/295 from the Estonian Committee on Bioethics and Human Research (Estonian Ministry of Social Affairs), using data according to release application nr T38 from the Estonian Biobank. For MoBa, informed consent was obtained from all study participants. The administrative board of MoBa led by the Norwegian Institute of Public Health approved the study protocol. The establishment of MoBa and initial data collection was based on a license from the Norwegian Data Protection Agency and approval from The Regional Committee for Medical Research Ethics. The MoBa cohort is currently regulated by the Norwegian Health Registry Act. The study was approved by The Regional Committee for Medical Research Ethics (no. 2012/67).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.