Operating two exchange-only qubits in parallel

Sensor dot readout

Readout of the exchange-only qubits is performed through PSB⁴¹, in which an electron either tunnels or remains confined, depending on its spin state. Nearby sensing dots, which function as single electron transistors (SET), are capacitively coupled to the quantum dot electrons and the conductance of SET will change depending on whether a charge tunnels or not. In this set-up, the change in the SET conductance is detected using a heterojunction-bipolar-transistor-based cryogenic amplifier⁴². The amplifier and SET are embedded in a lock-in detection circuit in which signals of around 50 μV_rms at 1 MHz are biasing one ohmic of the SET and the other ohmic is connected to the input of a dual-stage, AC-coupled voltage amplifier. Readout performance in this first-generation cryoamplifier is limited by noise, voltage division and bandwidth set by the 100-kΩ shunt resistors.

Device fabrication

All measurements are performed on an Intel Tunnel Falls device that was fabricated using state-of-the-art high-volume manufacturing techniques. The quantum dots are electrostatically confined in a two-dimensional electron gas (2DEG) defined by a Si/SiGe heterostructure. To protect electrons trapped in the quantum dots from incurring noise owing to surrounding nuclear spins, we use ²⁸Si, isotopically enriched to 800-ppm ²⁹Si remnants, to grow the quantum well. Although valley splittings were not measured on this particular device, we extract a range of 50–140 μeV for the one-electron valley splitting on devices from the same 300-mm wafer. More details on device fabrication can be found in ref. ⁷ and an extensive discussion on device uniformity is presented in ref. ¹.

Device tuning

A 2DEG is accumulated under gate electrodes P₁–P₃ and P₁₀–P₁₂ to facilitate access of the middle quantum dots to an electron reservoir. We tune quantum dots QD₄–QD₉ to the (1,3,1,1,3,1) electron occupation (charge stability diagrams are presented in Extended Data Fig. 2a,f,k,p,u). The two exchange-only qubits Q₁ and Q₂ are encoded on dots QD₄–QD₆ and QD₇–QD₉, respectively. QD₅ and QD₈ are populated with three electrons to increase the PSB readout window size that would otherwise be limited by valley splitting⁴³; this makes readout more robust against charge drift and miscalibration. PSB readout is established on dot pairs QD₄–QD₅ and QD₈–QD₉ to minimize crosstalk owing to capacitive coupling of quantum dots in the quantum dot array. Extended Data Fig. 5 demonstrates the necessity of a two-lattice-site separation between quantum dot pairs used for PSB in the scenario in which both quantum dot pairs are pulsed simultaneously for readout. Charge sensing is performed using two sensing quantum dots (SD₅ for Q₁ and SD₈ for Q₂) that host many electrons; these are placed on the opposite side of the central screening gate. With this readout arrangement, we find that the sensitivity of SD₅ to QD₈–QD₉ (performing PSB for Q₂) and of SD₈ to QD₄–QD₅ (performing PSB for Q₁) is small enough to not be a concern.

Definition of exchange-only qubits

To define an exchange-only qubit, three spins in three quantum dots are needed^13,14. The computational states of exchange-only qubits are defined as |0⟩ = |S⟩|↓⟩ (|0⟩ = |S⟩|↑⟩) and \(| 1\rangle =\sqrt\frac23| T_+\rangle | \downarrow \rangle -\sqrt\frac13| T_\rangle | \uparrow \rangle \) (\(| 1\rangle =\sqrt\frac23| T_+\rangle | \uparrow \rangle -\sqrt\frac13| T_\rangle | \downarrow \rangle \)), in which \(| S\rangle =\sqrt\frac12(| \uparrow \downarrow \rangle -| \downarrow \uparrow \rangle )\), \(| T_\rangle =\sqrt\frac12(| \uparrow \downarrow \rangle +| \downarrow \uparrow \rangle )\) and \( T\rangle _+=| \uparrow \uparrow \rangle \). The other possible states are leakage states outside the computational subspace, which have the same readout signature as the |1⟩ state. For qubit manipulation, the quantum dot pair with which PSB readout is performed defines the z axis of the Bloch sphere of the qubits and rotations around this J_z axis can be performed by turning on the exchange interaction between these quantum dots. The second axis of control is given by J_n, positioned at 120° from the J_z axis and can be controlled by turning on the exchange interaction between one of the quantum dots involved in PSB and the gauge spin (third quantum dot). We initialize the qubits using a charge-locking PSB readout sequence, recording the state of the system before qubit manipulation. Although this method is not scalable to larger systems as the fraction of accepted records is only 1/4^N for N qubits, it allows reducing the set-up complexity. An alternative initialization approach uses deterministic initialization by means of a reservoir⁴⁴. As we cannot discern the computational |1⟩ state from leakage states, only records indicating the computational |0⟩ state on both qubits can be used for data analysis. Although an external magnetic field is not strictly required for exchange-only qubit operation, as the gauge spin does not need to be initialized in a specific state, we apply a small 1-mT magnetic field to suppress nuclear spin dynamics²⁵. For more details on the exchange-only qubit encoding, see refs. ^13,14 and the Supplementary information.

Readout considerations for multi-exchange-only-qubit systems

Exchange-only qubits are encoded in a decoherence-free (or noiseless) subsystem of three spins in three quantum dots^13,14. In the tuning chosen here, the state of Q₁ (Q₂) can be determined by performiang PSB readout on the QD₄–QD₅ (QD₈–QD₉) pair. Neither of the exchange-only qubit computational states are ground states or eigenstates of the three-spin system, which implies that the qubits can be brought into leakage states through initialization, excitation, relaxation or dephasing. In particular, the computational states will be mixed with the leakage states during idle operations on the timescale of the singlet lifetime \(T_2^* \) (Extended Data Fig. 2). Experimentally, this implies that idle time, even for the initialized |0⟩ state, needs to be avoided. Similarly, any idle time introduced before readout will lead to information loss on the \(T_2^* \) timescale, rather than the single-spin relaxation time scale T₁ relevant for LD qubits. In turn, this means that we cannot simply perform sequential readout of both qubits as the second qubit would decay, unless (1) the readout integration time is much shorter than \(T_2^* \) (typically 2–3 μs in 800-ppm ²⁸Si but the readout integration time used in this experiment is 18 μs per PSB readout) or (2) we introduce dynamical decoupling to extend the lifetime of the idle qubit⁴⁵ or (3) we turn on a sufficiently large exchange such that the PSB pair Hamiltonian eigenbasis corresponds to the qubit readout basis⁴⁶ or (4) we involve ancillary quantum dots and swap the PSB quantum dot pairs away from each other such that both can be read in parallel with individual sensors. In our device, the two neighbouring sensors share an ohmic contact and part of the accumulated 2DEG, both with substantial series resistance. This couples the two SET drain currents, which in turn prohibits the fully parallel readout of neighbouring qubits, even though they have their own sensors. We need to either implement one of the solutions listed above or find new techniques that would allow us to recover the complete two-qubit information.

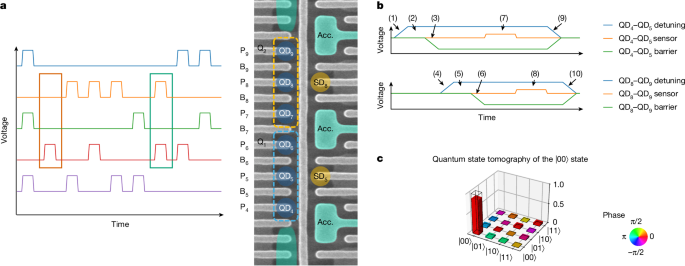
Charge-locking readout

Charge-locking readout is a multi-qubit readout protocol in which we first pulse all participating quantum dot pairs to their respective PSB readout window and only then start signal integration. In this manner, we prevent information loss through decoherence or relaxation while qubits are idling at their respective manipulation points (see Methods). This could be supplemented by the frozen PSB technique³⁰ if the relaxation times at the PSB window are not substantially longer than the signal integration time (steps 3 and 6 in Fig 1b). The steps of the charge-locking PSB readout are described as follows. (1) The first quantum dot pair used for PSB is pulsed into the readout window using a 21.84-ns-long voltage ramp. (2) At this readout point, a 3.64-ns wait time allows the spins to either be projected to a singlet and move to the (0,4) charge state or be projected to a triplet and remain in the (1,3) charge state. (3) The tunnel coupling between QD₄ and QD₅ can be lowered to suppress relaxation rates of these charge states³⁰. (4) After projection of the first quantum dot pair, the second quantum dot pair is ramped to its readout window, (5) spins are projected to the singlet or triplet states and (6) the charge relaxation rates are suppressed. We find the charges to be locked in the readout window, with relaxation times substantially longer than the integration time of 18 μs required to obtain a signal of sufficient quality. Therefore, we consider steps (3) and (6) not strictly necessary in our experiment. Once both qubits have been projected, a voltage pulse is applied to the SD₅ plunger to shift its electrochemical potential to the flank of a Coulomb peak to allow for charge sensing. (7) Then, a pulsed readout stimulus signal is applied to the sensor that allows determination of the state of Q₁. (8) After the readout of Q₁ is completed, the SD₅ plunger is brought back into Coulomb blockade and the process is repeated for Q₂. We achieve a signal-to-noise ratio of 4.25 and 3.10 for readout of Q₁ and Q₂, respectively. (9,10) At the end of the sequence, both qubits are pulsed back to their manipulation point.

Virtualization

To efficiently control the array of quantum dots, we use standard virtualization techniques^32,33. The relative effect between the dedicated plunger electrode and the surrounding plunger and barrier electrodes on the chemical potential of a quantum dot are measured by tracking electron addition lines in charge stability diagrams as a function of the applied voltages. These values are collected in the cross-capacitance matrix, which in turn is inverted to perform a linear basis transformation into the virtual voltage space. These virtual voltages now only affect the chemical potential of the quantum dot they are supposed to control, leaving the chemical potentials of other dots unaffected.

The voltage virtualization is fine-tuned after the quantum dot array is brought into the correct charge configuration and is isolated from the environment (Extended Data Fig. 2a,f,k,p,u). However, at that point, charge addition lines are no longer visible and cannot be used to update the voltage virtualization. Therefore, the crosstalk matrix entries are adjusted in an iterative process in which the position of inter-dot charge transition lines is monitored as virtual voltages on surrounding electrodes are changed. Proper virtualization is achieved once the position of charge transition lines does not change with altering virtual voltages. This procedure can be used for plunger–plunger as well as for plunger–barrier crosstalk compensation; the technique for barrier–barrier crosstalk compensation is described in the main text.

Barrier–barrier crosstalk compensation

To compensate the barrier–barrier crosstalk, the centre linecut of Fig. 2a is tracked as a function of the simultaneous barrier pulse amplitude vB₆ (Fig. 2e). As vB₆ is increased, we observe an increase of the exchange between QD₇ and QD₈, in line with our observations in Fig. 2c. We note that the exchange pattern is linearly shifted as a function of vB₆, indicating that the linear crosstalk compensation framework is applicable. The value of the crosstalk element is given by the slope of the resulting line pattern. We enter it into the existing voltage virtualization framework that relies only on a linear basis transformation. Also, we include finer corrections to compensate any outstanding movement along the detuning axis by optimizing barrier–plunger elements. Furthermore, we note a slight fingerprint shape change that reduces the exchange tunability during simultaneous exchange pulses as compared with individual exchange pulses for some of the quantum dot pairs (most notably B₅ and B₇). We account for this by adding small nearest-neighbour barrier–barrier elements to the cross-capacitance matrix (Extended Data Table 1). After the calibration cycle, we check the dependence of exchange strength as a function of the simultaneous barrier pulse amplitude (Fig. 2f) in comparison with the crosstalk-uncompensated situation (Fig. 2e). Using the described corrections, we observe that the resulting exchange pattern is independent of the simultaneously applied exchange pulse.

Exchange pulse calibrations

Exchange-only qubits are operated by issuing well-calibrated voltage pulses to dynamically control the exchange interaction between the relevant quantum dots^13,14. We choose to keep the durations t_p and t_b of the resulting exchange pulses equal and constant throughout the experiment. The rotation angle produced by an exchange pulse is given as φ = t_pJ(V_B) and we control it with the voltage V_B issued to the electrode controlling the exchange interaction. To calibrate each exchange axis, a qubit containing this exchange axis is encoded and prepared in its |0⟩ state, exchange pulses on the axis in question are applied and the qubit is read out. To ensure adequate measurement contrast (for example, to calibrate the J_z axis), pre-rotations or excitation swaps making use of previously calibrated axes are applied. Then, for each axis, the following three steps are performed:

• Fingerprint calibration. The goal of the fingerprint calibration is to ensure that exchange pulses are insensitive to charge noise in the double-dot detuning direction. Therefore, the exchange strength is measured as a function of barrier and detuning voltages²⁰. Then the crosstalk compensation between the exchange barrier electrode and involved plunger electrodes is adjusted to keep the sweet spot along the exchange axis at a constant detuning voltage. Extended Data Fig. 2b,g,l,q,v shows fingerprints for the exchange axis used in the experiment. Although this calibration can be performed with a single exchange pulse, we make use of an error amplification scheme by applying eight repeated exchange pulses to increase the sensitivity of the calibration.

• Initial exchange calibration. Next we measure the exchange coupling magnitude in the function of the barrier gate voltage at the selected detuning voltage. For this, exchange pulses of increasing amplitudes are applied and the |1⟩ state return probability is measured. The resulting data can be fit to b + acos(J(V_B)t_p), in which J(V_B) = αexp(γV_B) and γ is the exchange tunability.

• Fine exchange calibration. With an initial knowledge of J(V_B), it is possible to issue pulses of a desired rotation angle on this axis. To amplify the calibration error, a train of N pulses with a fixed rotation angle is measured. As the angle is swept, the resulting oscillations can be used to extract a more precise relation of J(V_B), which can be described as \(J(V_\rmB)=\alpha \exp (\gamma V_\rmB+\kappa V_\rmB^2)\), in which κ is a second-order correction to the exchange tunability. Further precision in the calibration can be gained by directly using a heuristic interpolation of J(V_B). The final calibration is presented in the Extended Data Fig. 2c,h,m,r,w.

Once the relation J(V_B) is established, pulses with rotation angle φ can be produced by issuing barrier pulses with amplitude

and

Furthermore, we ensure negligible error contributions from residual coupling \(J_\rmoff=J(V_\rmB_\rmoff)\) by reducing the voltage \(V_\rmB_\rmoff\) on the electrode when the exchange coupling is not active. We need to ensure that this condition is met and that rotation angles of up to 2π are available within the dynamic range of the arbitrary waveform generator (AWG). We achieve this by pulsing negatively on the barrier while its coupling is not active to make full use of the available dynamic range of the AWG.

Pulse pre-distortions

To minimize the effects of decoherence caused by magnetic noise from the spin bath, it is beneficial to operate with as-fast-as-practical exchange pulses. However, as pulse time t_p and buffer time t_b are reduced, the qubit fidelity is limited by non-Markovian control errors resulting from overlap of subsequent pulses owing to filtering effects of the transmission lines used to deliver the pulses. More concretely, the finite bandwidth of both the control electronics as well as the transmission lines results in the ideally square pulses produced by the control electronics being distorted. Although a systematic distortion that only affects the current pulse can be accounted for by standard calibrations, finite pulse fall times of one pulse that affect the amplitude of the subsequent pulse create an effective system memory. This system memory cannot be accounted for by only using standard calibrations. Further effects leading to a system memory can include pulse reflections at impedance mismatches in the signal chain or the high-pass effect of the bias tees used. To counter these effects, we implement exponential undershoot/overshoot pulse pre-distortions. Properly pre-distorted pulses avoid pulse overlap and reduce the pulse rise and fall time^47,48.

We tackle the task of finding the appropriate pre-distortions in two steps. First, we introduce a buffer time spectroscopy measurement in which t_b is varied for a train of pulses with varying amplitudes (Extended Data Fig. 3). Tracking the voltage at which a particular overall rotation angle is achieved as a function of t_b gives a good approximation to the step response. On the basis of this dependence, exponential parameters are extracted to define the pre-distortion coefficients for short (about 8 ns) and medium (about 50 ns) timescales.

The pre-distortion corrections are applied in real time at the last output stage of the AWG. The effect of pre-distorted pulses can be assessed by taking another buffer time spectroscopy measurement for which now the approximate step response for these timescales is substantially flatter. However, these corrections still leave long pulse sequences of several thousand exchange pulses vulnerable to effects on longer timescales.

To further reduce the effect of non-Markovian errors on longer timescales, a second step to optimize the best pre-distortion parameters is performed. As the cost function of the optimization procedure, we choose the visibility of a sequence of random Clifford gates (difference between the recovered |1⟩ and |0⟩ states). To reduce the complexity of the procedure, the same pre-distortion parameters are applied on all control lines. We find that an exponential model with a timescale of about 500 ns describes the filter function of the transmission lines well. We choose to apply these corrections pulse by pulse by modifying the amplitude of the exchange pulses based on the history of exchange pulses on the respective channel rather than applying them sample by sample. This is why Extended Data Fig. 1 can show a time-dependent oscillation frequency but we can still measure high-fidelity exchange pulses over extended periods of time. Otherwise, this technique follows the same mathematical framework. This procedure can be further improved by designing a targeted error-amplifying sequence to act as the cost function for the optimization.

Exchange-only gate library

General single-qubit gates for exchange-only qubits need to be synthesized from positive angle rotations around the n and z axes^13,14. The precise decomposition of Clifford gates to n-exchange and z-exchange pulses can be found in ref. ²⁴. With this decomposition, a single-qubit Clifford gate needs on average 2.666 exchange pulses.

Two-qubit gates for exchange-only qubits are also composed only of exchange pulses. However, the precise pulse sequence, and therefore also the number of pulses and the duration of the gate, depend on the connectivity between the qubits as well as their configuration. The two-qubit gate library implementation of ref. ⁴⁹ is used to determine the appropriate sequence of pulses. The two-qubit gates supported in this library are CNOT, iSWAP and SWAP. Of the 11,520 two-qubit Clifford gates, 576 contain no two-qubit gate, 576 include a SWAP, 5,184 include a CNOT and 5,184 include an iSWAP gate, with an average of 32.3 exchange pulses.

To improve the efficiency of pulse execution on two qubits, exchange pulses can be applied in parallel. This can be done straightforwardly in the case of single-qubit gates on the respective qubits. For two-qubit gates, an algorithm that issues pulses ‘as soon as possible’ for the two-qubit gate sequence while avoiding scheduling pulses on neighbouring barriers is used. A general two-qubit Clifford gate can be decomposed into single-qubit Clifford gates acting on either qubit, followed by a two-qubit gate, followed again by single-qubit Clifford gates acting on either qubit. We implement the parallelization of a general two-qubit Clifford gate by parallelizing its respective parts.

Mirroring gates for exchange-only qubits

The flexibility of exchange-only qubits can further be enhanced by the use of mirroring gates. Which exchange axis is responsible for n rotations and which axis is responsible for z rotations—the configuration of the exchange-only qubit—is defined by the location of the quantum dot pair that performs PSB readout. This gives each exchange-only qubit two possible configurations. The configuration can be changed by choosing the other possible quantum dot pair to perform PSB readout or it can be changed in situ, by applying mirroring gates consisting of three exchange π-pulses around the n− , z− and n− axes. Here changing the quantum dot pairs performing readout is not possible but applying mirroring gates after initialization and before readout provide us with this extra flexibility. Choosing the optimal combination of configurations for the two qubits has two advantages. First, two-qubit gates with fewer pulses can become available⁴⁹, reducing overall two-qubit gate complexity. Second, because gates have an unequal distribution of pulses on the various exchange axes, fewer pulses can be scheduled on exchange axes with reduced quality factors, increasing average gate fidelity.

Randomized benchmarking

We choose to use RB as the primary tool to characterize the fidelities of single-qubit and two-qubit gates. For RB, a random sequence of N single-qubit or two-qubit Clifford gates is applied, followed by a recovery gate that returns the qubit(s) to a known state. The Clifford gates are decomposed into exchange pulses as described in the previous section. By interpolating the state recovery probability as a function of N, the average error per Clifford gate can be extracted. In more detail, for the single-qubit experiments, we use a technique called blind RB²⁴, in which each seed is run twice, recovered one time to |0⟩ and another time to |1⟩. Analysis of the resulting curves allows extraction of the leakage error per Clifford, which we find to be in line with expectations given pulse durations and abundance of nuclear spins (see the main text).

When performing parallelized RB, single-qubit gates are issued at the same time on the respective qubits and the parallelized versions of the two-qubit gates in the gate library are used. We also emphasize that the full two-qubit state readout is performed. This ensures that state leakage is properly accounted for, which can be challenging when only partial information of the two-qubit state is extracted (Extended Data Fig. 4). For single-qubit and two-qubit RB, we report the mean fidelity and error of the mean of five measurements that each are averaged over 20 random seeds. For interleaved two-qubit RB, we use five measurements with 25 random seeds each.

Monte Carlo simulation

To improve our understanding of the system, we estimate the impact of magnetic noise and charge noise with a Monte Carlo simulation by assuming quasi-static noise δB and δJ on both the Zeeman and exchange coupling, respectively. The two-qubit gate fidelity is then calculated as the average projection of the expected state with that of the final state for all computational states. The magnitude of δB is chosen to fit the average pure dephasing time \(\overlineT_2^* \), calculated as \(\frac1\barT_2^* =\sqrt\sum _n^N\left(\frac1nT_2^* \right)^2/N\) of the N quantum dot pairs involved, in which \(\genfrac0exn\,T_2^* \) is the singlet lifetime in the nth double dot (Extended Data Fig. 2e,j,o,t,y). An appropriate δJ is chosen to fit the number of resolvable exchange oscillations N_osc for each of the exchange axes (Extended Data Fig. 2d,i,n,s,x). We note that the evolution of the exchange coupling remains coherent well past the decay of the fixed frequency fit. The parameter N_osc is extracted by fitting a Gaussian decay to the oscillation envelope, providing a better estimate for the impact of charge noise as it is insensitive to small changes in the exchange oscillation frequency²⁵.