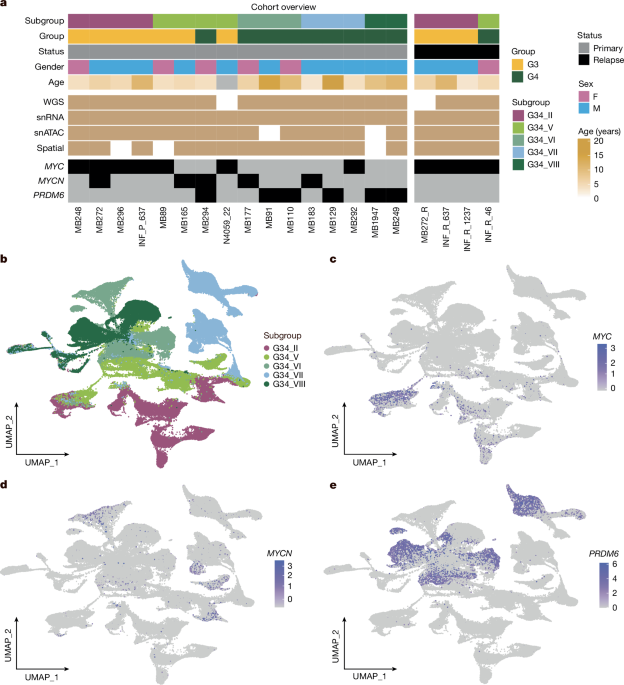
Target cohort selection and verification
Target tumour tissue samples were collected from global medulloblastoma published materials (ICGC2, fresh-frozen paraffin-embedded (FFPE)13 and Individualized Therapy For Relapsed Malignancies in Childhood (INFORM)39 cohorts). For each selected case, the copy number/structural variant profiles from methylation and/or WGS data were used to identify MYC/MYCN amplification and SNCAIP structural variant presence. Bulk gene expression RNA-seq profiles from these samples were used to inspect MYC/MYCN/SNCAIP/PRDM6 expression as well. For some cases with sufficiently available FFPE material, further FISH experiments were performed to verify the selection (details in Supplementary Table 1). No statistical methods were used to predetermine sample size.
Single-nucleus multi-omics sequencing
Flash-frozen tumour samples were processed to extract nuclei as described earlier27. Extracted nuclei were processed using Chromium Single Cell Multiome ATAC Gene expression kit and Chromium Controller instrument (10x Genomics) as per manufacturer’s recommendations. One sample, MB248, was processed with Chromium Next GEM Single Cell 3′ reagent kit as per the manufacturer’s recommendation. In total, 15,000–20,000 nuclei were loaded per channel along with the multiome gel bead. Libraries were quantified using Qubit Flurometer (Thermo Fisher Scientific) and profiled using Fragment Analyzer. snRNA-seq and snATAC-seq libraries were sequenced using a NextSeq2000 to the recommended lengths. If the snATAC-seq library was not of good quality, we still used the obtained snRNA-seq library if that was found to be appropriate on the basis of quality control parameters. snRNA-seq and snATAC-seq datasets were further analysed separately.
snRNA-seq data analysis
De-multiplexed reads were aligned to human genome assembly GRCh38 (v. p13, release 37, gencodegenes.org). Comprehensive gene annotation (PRI) was customized by filtering to transcripts with the following biotype: protein coding, lncRNA, IG and TR gene and pseudogene as recommended for cellranger mkgtf wrapper. Reads were aligned using STARsolo with parameters: –soloType CB_UMI_Simple –soloFeatures Gene GeneFull –soloUMIfiltering MultiGeneUMI –soloCBmatchWLtype 1MM_multi_pseudocounts –soloCellFilter None –outSAMmultNmax 1 –limitSjdbInsertNsj 1500000. For overlapping genes for which intronic alignment recovered low counts, exonic alignment counts were used. Cells were separated from debris using the diem pipeline40. Cells with mitochondria fraction above 2%, number of detected genes above 6,600 and an intronic fraction (number of reads aligned to intron/total number of reads aligned to exon + intron) less than 25% were also filtered out. Filtered cells were corrected for background signature using the SoupX pipeline41. Finally, the scrublet42 tool was used to remove putative doublets. Further, the gene expression matrices from all samples were merged together in the full matrix and processed by means of the Seurat package43 to normalize, compute top principal complements (n = 30), find most highly variable genes (n = 2,500) and visualize by means of UMAP. After distinguishing non-tumour cells on the basis of corresponding markers and combined UMAPs, per sample processing was performed using the Seurat toolkit using the same settings combined with cell clustering. The enrichment of proliferation, differentiation and progenitor-like activity of medulloblastoma-specific markers per cell was performed using the single sample function from the GSVA R package44 using two independent reference datasets8,9. Cell clusters enriched with proliferation signals were selected and marked on the basis of maximum GSVA signal enrichment from manual inspection per sample.
snATAC-seq data analysis
ATAC-seq reads were aligned to GRCh38 using the Cellranger arc wrapper. The selected cells were processed using the Signac R package45 to filter the doublets/outliers on the basis of signal per cell distribution analysis and to inspect the cell compartments by means of UMAP visualization after normalization and identification of the most highly variable regions. snRNA-seq data information was used to annotate the cells from corresponding processed data.
To identify differentially enriched cis-regulatory elements per sample per annotation, peaks were first called on the merged snATAC-seq data using the ArchR R package46 by first creating pseudobulk replicates using addGroupCoverages (minCells=2000, maxCells=5000, minReplicates=2, maxReplicates=5, groupBy=“Sample”, maxFragments=100 * 10^6) and calling reproducible peaks using addReproduciblePeakSet(groupBy=“Sample”, maxPeaks=150000). Obtained peaks were further filtered on the basis of presence in at least 5% of cells in any sample. Marker peaks were then obtained using getMarkerFeatures() on the basis of subclonal annotation and filtering on the basis of area under the curve > 0.52 and false discovery rate (FDR) < 0.01.
Genes correlated to the peaks were identified using addPeak2GeneLinks() using the subset of cells with dual snRNA-seq and snATAC-seq profiles in the merged data. Correlated genes (more than 0.1) were intersected with peaks associated with genes identified on the basis of GREAT47 annotation to identify the robust pairs of peaks to gene links.
Single-cell CNV phylogeny reconstruction
Initially, CNV analysis was performed on a subset of samples (n = 2 for each oncogene) using the InferCNV tool14 on the raw gene expression matrix with droplet protocol adjusted parameters (average read counts cutoff 0.5, smooth method runmeans, denoise active) and hierarchical clustering by means of the ward.D2 method to derive the clonal phylogeny. The main subclones obtained from this phylogeny demonstrated a close match to the initial Seurat clustering results (mean purity evaluation metrics across samples: 0.921). To further improve the visualization and increase computational efficiency, the CNV analysis was performed on the full cohort by transferring single cells into meta-cells, on the basis of the established method48. For this purpose, we computed the sum of gene expression counts across n = 5 cells combined within the clusters derived from Seurat processing. The meta-cell InferCNV calling was performed for each sample separately with read counts cutoff 0.5, and the phylogeny clustering results were visualized in UMAPs with k as number of clusters, varying from 2 to 5. Differentially expressed genes for identified subclones per sample were computed by means of a Wilcoxon rank sum test. Significant MYC/MYCN/PRDM6 differential expression and progenitor-like activity enrichment values were computed per cell to finalize the derived phylogeny cut limit for each case after manual inspection. The selected cut limit for the number of subclones in the phylogeny was verified by using random tree subcluster partition in the phylogeny reconstruction with a minimum P < 0.05.
All tumour samples (n = 16) were also merged together and CNV profiling was performed to verify the status of non-tumour cells. The annotation of verified normal cells was further used as reference control for each sample.
For snATAC-seq data, a matrix with all genomic regions as raw and read counts per column per sample was used to adjust for InferCNV input format. Further meta-cell formation and the same CNV calling procedure as for snRNA-seq were performed on the derived matrices. The subclone annotation derived from snRNA-seq data was used to assign corresponding cluster phylogeny per sample.
Interactive CNV visualization for the results from snRNA-seq and snATAC-seq data per sample is available through ShinyApp: http://kokonech.shinyapps.io/mbOncoAberrations.
Mutation calling from snATAC-seq data
For n = 3 MYC cases the number of reads in snATAC-seq data was increased up to 3 × 109 per sample to have sufficient coverage for mutation calling. The alignment of novel reads was performed using the same strategy as described above. Initial subclone annotation was used to classify the cells. Afterwards, the mutation calling was performed using the SComatic method49 on the BAM files extracted for each subclone. Initial mutation filtering was performed on the basis of inspection of somatic mutations derived from WGS data2 as the main control. Results were also confirmed using the bcftools method50 on the full merged pseudobulk snATAC-seq data with standard settings. The VAF from the full merged pseudobulk mutation calling was used to compare with the VAF from bulk control results. The visualization of somatic mutation presence across subclones per sample was performed by means of the R package ComplexHeatmap. For more relaxed filtering control, blood bulk WGS control was applied to exclude non-somatic mutations, while mutation filtering limits were strengthened: min coverage 20× and minimum support 5×. Annotation of identified mutations was performed using Annovar toolkit51 using gencode v.38 materials.
Single-cell DNA and RNA sequencing procedure
Flash-frozen tumour samples were processed to extract nuclei as described previously52. Single nuclei were sorted into the wells of DNA LoBind 96-well plates using fluorescence activated cell sorting. Each plate was used for downstream genome and transcriptome isolation, reverse transcription of the transcriptomes and primary template-directed amplification using the ResolveOME Multiomic kit from Bioskryb, according to the manufacturer’s protocol. Selected wells were used for quality control before library preparation to assess the quantity and quality of the extracted genome or transcriptome DNA, using the 4200 TapeStation System. Sequencing libraries were prepared using Illumina-compatible unique dual index adaptors, according to the manufacturer’s protocol as provided in the ResolveOME kit. After amplification, barcoded libraries were pooled and purified using Ampure Beads to select 250–1,000-base pair (bp) fragments with an average peak size of 400–500 bp. Multiplex libraries were sequenced using one lane of the NovaSeq 6000 System each, with 100-bp paired-end sequencing for the genome libraries and 100-bp single-read sequencing for the transcriptome libraries.
Single-cell DNA and RNA sequencing data analysis
DNA sequencing reads per cell were initially processed (quality control, alignment) by means of the BJ-DNA-QC Nextflow-based pipeline from BioSkryb using hg38 as the main reference. CNV profiling was performed with the Ginkgo tool53 on the basis of resolution 100 kilobases (kb). Outlier signal adjustment was performed on the basis of cut for mean plus 2 s.d. Heatmap visualization was performed by means of the ComplexHeatmap R package using the clustering method ward.D2 with Euclidean distance.
RNA-seq reads per cell were aligned to the hg38 reference by means of the STAR tool54. Gene expression counts were computed by means of the FeatureCounts option from the Subread toolkit55 using gencode v.38 reference. Combined gene expression matrix analysis was performed by means of the Seurat toolkit43. Non-tumour cells as well as subclone specificity were identified on the basis of the inspection of known gene markers and projection into snRNA-seq profiles using the transfer Seurat R toolkit function.
Molecular cartography
The specific gene set (n = 100) covering group 3/4 known driver genes alongside marker genes of the developing cerebellum non-malignant cell types was selected for the protocol (Supplementary Table 7). The gene selection was on the basis of specific properties. First, the main selection was split into two blocks: tumour-specific genes (60%) and normal cell markers (40%). The tumour-specific genes had several blocks of selection: (1) known target markers of group 3/4 tumours including MYC, MYCN, SNCAIP and PRDM6; (2) proliferation, differentiation and cell-cycle activity markers; (3) cells-of-origin-associated markers. The normal cell type markers were selected on the basis of knowledge about normal cell types of the cerebellum that could also be present in the tumour. For each cell type, at least two markers were selected. All selected genes were also verified on available snRNA-seq data as well as bulk profiles.
Optimal cutting temperature compound (OCT)-embedded samples were cryo-sectioned into 10-µm sections onto a molecular cartography slide. Fixation, permeabilization, hybridization and automated fluorescence microscopy imaging were performed according to the manufacturer’s protocol (Molecular preparation of human brain (beta), Molecular colouring, workflow setup) as described previously52.
Spatial data analysis
The detection of cell boundaries was performed with CellPose56. Afterwards, gene expression counts were computed per cell and extracted using further custom Python scripts. Initial cell filtering was performed by assigning the minimum number of counts/genes per cell and size of the cells. Afterwards, the analysis of the formed gene expression matrix, including clustering and UMAP visualization, was executed using the Seurat toolkit43. Annotation of cell states and types was achieved through direct projection with the snRNA-seq data by means of transfer function and verified by visual inspection of marker genes. Spatial-specific analysis, the detection of closest cell connections, was conducted using the Giotto toolkit57.
Deconvolution analysis of MYC/MYCN cases
The assigned MYC/MYCN single-cell dataset (MB272) with annotation of compartments was used as reference control for the CIBERSORT method58 to perform deconvolution on a set of bulk FFPE medulloblastoma RNA-seq profiles from MYC/MYCN samples13. For each case, MYC/MYCN status was derived from methylation copy number profile. The deconvolution values obtained from CIBERSORT results were visualized by using the ComplexHeatmap R package in order to demonstrate compartment enrichments per sample.
Survival analyses on the basis of expression of MYC as well as the computed deconvolution of MYC compartment proportion of multiple genes were performed using the Kaplan–Meyer algorithm with applied Bonferroni correction for multiple testing. The resulting plots were generated by means of the R2 Genomics Analysis and Visualization Platform (http://r2.amc.nl).
Bulk RNA-seq data analysis
Bulk RNA-seq data from the ICGC cohort overlapping with WGS data were available for 85 group 3/4 medulloblastomas of our cohort2. We performed GSVA on reads per kilobase of transcript per million mapped read scores using the R package GSEABase. We used the following gene sets: MYC target genes: ‘HALLMARK_MYC_TARGETS_V2’, ‘MYC_UP.V1_UP’, ‘DANG_MYC_TARGETS_UP’26; S-phase genes: ‘REACTOME_S_PHASE’, ‘SA_G1_AND_S_PHASES’.
Extended gene expression and associated CNV profile metadata for 405 group 3/4 medulloblastoma samples were integrated for inspection of common CNV gains/losses3. The chromosomal arm gains or losses as provided in this corresponding study were binarized. DESeq2 was used to compute differentially expressed genes using lfcShrink(type=“apeglm”) and filtered using adjusted P < 0.001 and log fold change (lfc) > 0.5 criteria to obtain a list of statistically significant altered gene expression. We then used msigdbr and clusterProfiler R packages to identify chromosomal loci of the differentially expressed genes.
Additionally evident differentially expressed genes (adjusted P < 0.05) among the central nervous system tumours provided in the corresponding study24 were inspected to identify those that are specific for common group 3/4 gain (overexpressed, lfc > 0.5) and loss (low expressed, lfc < 0.5) regions.
WGS data
Mutation calls (SNVs, indels, CNVs and structural variants (SVs)) of previously published WGS data from medulloblastomas of all subtypes were taken from the ICGC dataset2. Only samples from primary tumours with clear subtype annotation and clear ploidy status were included; see Supplementary Table 5 for an overview on these samples and associated clinical data.
Driver mutations (SNVs and CNVs)
Non-synonymous SNVs, small indels and small structural rearrangements (amplifications, defined as copy number gains ≥ 10, homozygous deletions with less than 0.9 copy numbers and translocations with a minimal event score of 5) were classified as driver mutations if they targeted a splice-site or an exonic region of PRDM6, MYC or a gene listed as a putative driver of medulloblastoma in the cancer driver database intogen59 (release date 31 May 2023). Moreover, we included TERT promoter mutations at hg19 positions 1295228 and 1295250 as drivers. High-level amplifications affecting MYC or MYCN (identified from methylation/WGS copy number profiles) and duplications of SNCAIP, leading to overexpression of PRDM6 (identified from WGS SV calling), were additionally integrated from a previous global data analysis2.
Large-scale CNVs were defined as CNVs spanning at least 1 Mb and with a coverage ratio less than 0.9 or a coverage ratio greater than 1.1, according to the output by ACEseq. Retained CNVs with a size of at least 25% the size of the p arm of a respective chromosome were further classified as affecting both arms if the CNV spanned the centromere, or else as affecting the p arm or the q arm. Among these CNVs, we tested for positive enrichment of particular chromosomes in the cohort using a binomial test with success probability 1/24 (that is, assuming that each chromosome has equal probability to be affected by the CNV). Chromosomes with an adjusted P < 0.05 (Holm’s correction) were classified as likely drivers of medulloblastoma. This analysis was separately performed for gained and lost chromosomes. Among group 3/4 medulloblastomas, we identified gains of chromosomes 4, 7/7q, 12 and 17/17q and losses of chromosomes 8, 10/10q, 11 and 17p as significant. We augmented this list by gains of chromosomes 18 and 1q and loss of 5q, as was reported previously60.
Timing of CNVs, ECA and MRCA
Quantification of mutation densities at copy number gains was performed using the R package NBevolution v.0.0.0.9000, which is described in detail in the corresponding study23. In brief, we counted clonal mutations separately on each autosome, stratified by copy number state using the function count.clonal.mutations() with max.CN=4, excluding chromosomal segments with length less than 107 bp. count.clonal.mutations() fits a binomial mixture model with success probabilities according to the expected mean values of the clonal VAF peaks, which, for an impure sample with tumour cell content \(\rho \), are given by
$$\rmVAFs\in \left\\frac\rho \zeta ,\frac(\rmCN-b)\rho \zeta ,\fracb\rho \zeta \right\,$$
(1)
where CN denotes the copy number of a given segment, b denotes the copy number of the minor allele (that is, the allele with the smallest number of copies) on this segment and
$$\zeta =\rho \rmCN+2(1-\rho )$$
(2)
is the average copy number of a given locus in the sample. Mutation densities (SSNVs per bp) at MRCA and ECA, denoted by \(\widetildem_\textMRCA\) and \(\widetildem_\textECA\), respectively, were computed using the function MRCA.ECA.quantification(). In brief, MRCA.ECA.quantification() first estimates \(\widetildem_\textMRCA\) from the number of all clonal mutations and the total size of the analysed genome, \(g=\sum _lg_l\), where the index \(l\) labels individual segments contributing to the analysis, yielding
$$\mathopm\limits^ \sim _\rmM\rmR\rmC\rmA=\sum _l\fracn_1,l+n_\rmC\rmN-b,l(\textCN_l-b_l)+n_b,lb_lg\,\textCN_l,$$
(3)
where \(n_k,l\) denotes the number of clonal mutations present on \(k\) copies of the \(l\)-th segment. Note that \(\widetildem_\textMRCA\) normalizes mutation densities per copy and hence can be interpreted as molecular time. The function MRCA.ECA.quantification() also computes lower and upper 95% confidence bounds for \(\widetildem_\textMRCA\) by bootstrapping the genomic segments 1,000 times. In the next step, MRCA.ECA.quantification() asks for evidence for an earlier common ancestor in the data. If a chromosomal gain occurs concomitantly with the onset of tumour growth, the density of amplified clonal mutations (that is, present on multiple copies of a gained allele) will, on average, be equal to the density of clonal mutations on non-amplified chromosomes or chromosomal regions. By contrast, if a chromosomal gain occurs earlier, the density of amplified clonal mutations on the gained allele will be smaller than the density of clonal mutations on non-amplified chromosomes or chromosomal regions. To distinguish these two cases, MRCA.ECA.quantification() tests for each gained segment whether or not the density of amplified clonal mutations agrees with the mutation density at MRCA, on the basis of a negative binomial distribution. If the mutation density of amplified clonal mutations is significantly smaller than the mutation density at MRCA, the segment is assigned to an earlier time point or else to the MRCA. MRCA.ECA.quantification() then asks whether segments assigned to earlier time points emerged in the same time window or during different time windows. We define as the null hypothesis that all CNVs emerged in an ECA. To test the null hypothesis, MRCA.ECA.quantification() computes the mutation densities at the ECA from the number of clonal mutations on the amplified minor allele, \(n_b,l\) (if b > 1), and from the number of mutations on the amplified major allele, \(n_\textCN-b,l\), as
$$\widetildem_\rmECA=\frac{\sum _l,P_\rmadj,l\le 0.01n_b,l+n_\rmCN-b,l}{\sum _l,P_\rmadj,l\le 0.01g_l,b+g_l,\rmCN-b},$$
(4)
where \(P_\rmadj,l\) is the adjusted P value of segment l belonging to the MRCA, and \(g_l,b\) and \(g_l,\textCN-b\) are the length of segment l, contributed by the amplified minor and major alleles, respectively. In analogy to \(\widetildem_\textMRCA\), MRCA.ECA.quantification() also estimates lower and upper 95% confidence bounds by bootstrapping. On the basis of a negative binomial distribution (and an FDR of 0.01), MRCA.ECA.quantification() then tests for each early segment whether or not its mutation density indeed conforms to a joined ECA, as defined by \(\widetildem_\textECA\). Only segments with mutation densities conforming to \(\widetildem_\textECA\) are assigned to the ECA, whereas all other segments are reported as conforming neither to the ECA nor to the MRCA.
Upon timing MRCA and ECA for each sample, we translated mutation densities into weeks post conception (p.c.) by inferring SSNV rates per diploid genome and embryonic day (\(\mu \lambda \)), using the measured VAF distributions and age at diagnosis as outlined below in section ‘Real-time estimate of cell division rate’. As mutation calling was performed by comparing tumours against a matched blood control, mutation densities correlate with the time after gastrulation (at approximately 2 weeks after conception). Thus, the mutation density per haploid genome (3.3 × 109 bp), \(\widetildem\), relates to the time p.c. according to \(\widetildem(t)=\frac\mu \lambda \rmday\frac13.3\times 10^9(t-14\,\rmd)\). The estimated time of birth was taken as 38 weeks after gastrulation (40 weeks p.c.).
Timing of SNVs and small indels
We classified SNVs and small indels as subclonal or clonal on the basis of the number of variant reads, \(n_\mathrmvar\), the number of reference reads, \(n_\textref\), tumour purity \(\rho \) and copy number \(k\). Specifically, mutations were classified as subclonal if the probability to sample at most \(n_\mathrmvar\) variant reads out of \(n_\mathrmvar+n_\textref\) total reads according to a binomial distribution with success probability \(\frac\rho \rho k+2(1-\rho )\) was smaller than 5%. If a mutation was classified as clonal and fell on a region with \(k=3\), we moreover classified the mutation as early clonal (that is, acquired before the chromosomal gain on the gained chromosome and hence present on at least two copies) if the probability to sample at most \(n_\mathrmvar\) variant reads out of \(n_\mathrmvar+n_\textref\) total reads was at least 5% according to a binomial distribution with success probability \(\frac2\rho \rho k+2(1-\rho )\), or else as late clonal.
Modelling medulloblastoma initiation
We modelled medulloblastoma initiation and growth with a population genetics model originally developed for neuroblastoma, as described previously23. In brief, the model assumes that disease initiation is driven by two consecutive drivers in a transiently expanding tissue of origin, which for group 3/4 medulloblastoma is probably the population of unipolar brush cell progenitors (UBCPs16,17,24). The two driver events are associated with the ECA and the MRCA of the tumour, and spawn, respectively, a pre-malignant and the malignant tumour clone. We assumed that both drivers occur with small probabilities \(\mu _1\) and \(\mu _2\) during cell divisions, and confer a selective advantage (\(r\) and \(s\), respectively) that acts by reducing cell differentiation. Moreover, we assumed that UBCPs acquire on average \(\mu \) neutral somatic variants per cell division, which we modelled with a Poisson process. The population of UBCPs has been experimentally described from week 9 p.c. until the time of birth24,27. To capture this trend, we modelled an initial phase of exponential growth at rate \(\lambda _1-\delta _1,\,\lambda _1 > \delta _1\) until time \(T\), where \(\lambda _1\) and \(\delta _1\) denote the division and differentiation rate, respectively, and a subsequent phase of exponential decline at rate \(\lambda _2-\delta _2,\,\lambda _2 < \delta _2\).
Following refs. 23,61, we calculated the probability of the MRCA to occur at time t according to
$$P_\rmMRCA=\left\{\beginarraycP_\rmMRCA,\rmI,\,t < T\\ 1-(1-P_\rmMRCA,\rmI)(1-P_\rmMRCA,\rmII)(1-P_\rmMRCA,\rmIII),\,t\ge T\endarray,\right.$$
(5)
with40
$$P_\rmMRCA,\rmI(t)\,=\,\mathop\sum \limits_x=1^N(t)-1e^-\mu _1(x-1)(1-e^-\mu _1)\left(1-\exp \left\-\frac\mu _1\mu _2\lambda _1TN(t)F1-\frac\delta _1\lambda _1\right\\right),$$
$$P_\rmMRCA,\rmII(t)=1-\exp \left(-\frac\mu _1\mu _2\lambda _1\lambda _2\nu _2,\rmDT\lambda _2-\delta _2/rN(T)\e^(\lambda _2-\delta _2/r)(t-T)-1\\right),$$
$$P_\rmMRCA,\rmIII(t)=1-\exp \left(-\frac\mu _1\mu _2\lambda _2^2\nu _2,\rmDN(T)\delta _2\left(\frac1r-1\right)\left\{\frace^(\lambda _2-\delta _2)(t-T)-1\lambda _2-\delta _2-\frace^\left(\lambda _2-\frac\delta _2r\right)(t-T)-1\lambda _2-\frac\delta _2r\right\}\right),$$
where \(\nu _2,\rmD=1-\frac\delta _2s\lambda _2\) is the survival probability of a cell undergoing the second oncogenic event while the population decays, \(F=\int _^1\nu _2,E/(\nu _2,Ez^\alpha )dz,\,\nu _2,E=1-\frac\delta _1s\lambda _1\) and \(\alpha =\frac\delta _1-s\lambda _1\delta _1-\lambda _1\). Moreover, we calculated the probability of the ECA to occur at \(t_1\), conditioned on the MRCA occurring at \(t_2\), as described previously23
$$P(t_1|t_2)=\fract_1t_2;t_1 < t_2\le T,$$
and
$$\beginarraylP(t_1|t_2)\,=\\ \frac\Theta (T-t_1)\lambda _1\delta _2\left(1-\frac1r\right)t_1+\Theta (t_1-T)[\lambda _2+\lambda _1T\delta _2(1-1/r)-\lambda _2e^\delta _2(1-1/r)(T-t_1)]\lambda _2+\lambda _1T\delta _2(1-1/r)-\lambda _2e^\delta _2(1-1/r)(T-t_2);\\ t_2 > T,\endarray$$
(6)
where \(\Theta (\bullet )\) is the Heavyside step function and \(0\le t_1 < t_2\).
To estimate the model parameters from the WGS data, we contrasted the probability of acquiring the first and second drivers with the measured distribution of SNV densities at ECA and MRCA in group 3/4 medulloblastomas using approximate Bayesian computation with sequential Monte-Carlo sampling (ABC-SMC), as implemented in pyABC62. We used a population size of 1,000 parameter sets and 25 SMC generations or \(\varepsilon \le 0.05\) as termination criteria. The model fit was performed in analogy to Körber et al.23 (code and pseudo-code are available at https://github.com/kokonech/mbOncoAberrations). 95% posterior-probability bounds for the model fits were estimated by simulating the model with each sampled parameter set and cutting off 2.5% at each end of the simulated distribution.
Modelling medulloblastoma growth
We modelled medulloblastoma growth from the MRCA as exponential growth with rate \(\lambda _T-\delta _T\), where \(\lambda _T\) denotes the division rate and \(\delta _T\) the loss rate (owing to differentiation or death) in the tumour. Denoting the number of tumour cells with \(N_T(t)\) and assuming that neutral mutations are on average acquired at a rate \(\mu \lambda _TN_T(t)\) per haploid genome during tumour growth, the site frequency spectrum of neutral variants at \(t_\textend\) is, on average63,
$$S_k(i,\mu )=\int _^t_\textendP_1,i(\lambda _T,\delta _T,t_\textend-t)\mu k\lambda _TN_T(t)dt,$$
(7)
where \(k\) is the chromosomal copy number, and \(P_1,i(\lambda _T,\delta _T,t_\textend-t)\) is the probability to grow from a single cell to a clone of size i within a time span \(t_\textend-t\), according to a supercritical linear birth–death process (for example, see ref. 64).
To estimate \(\mu \) and \(\delta _T/\lambda _T\) from the WGS data, we followed the strategy described previously23 to compare \(M_k(a,\mu )\), the cumulative allele frequency histogram of variants present in at least \(a\) cells in regions with copy number \(k\), given a mutation rate \(\mu \), between model and data. Here,
$$M_k(a,\mu )=\mathop\sum \limits_i=a^bS_k(i,\mu )\approx \int _^t_\textend\mu k\lambda _TN_T(t)\fracP_1,b(\lambda _T,\,\delta _T,t_\textend-t)-P_1,a(\lambda _T,\,\delta _T,t_\textend-t)\log \beta (t_\textend-t)dt,$$
(8)
$$\beta (t)=\frac\lambda _T(e^(\lambda _T-\delta _T)t-1)\lambda _Te^(\lambda _T-\delta _T)t-\delta _T.$$
To this end, we used ABC-SMC62 with a population size of 1,000 parameter sets and 25 generations or \(\varepsilon \le 0.05\) as termination criteria. To learn the dynamics of tumour growth with confidence, we included tumours with well-defined subclonal tails and no evidence for subclonal selection. Tumours were selected (Supplementary Table 5) on the basis of visual inspection of the VAF histograms, to remove cases with poor subclonal resolution. In addition, we removed cases without age information and those with evidence for subclonal selection as suggested by the evolutionary model implemented in Mobster65 (setting autosetup = ‘FAST’), which we ran on autosomes and upon computing pseudo-heterozygous VAFs, \(\widetilde\textVAF\), defined as 50% of the mutant sample fraction, SF (hence, \(\widetilde\textVAF=\frac\zeta 2k\rmVAF\), where \(k\) is the number of alleles carrying the mutation and VAF is the actual VAF). For the 35 retained group 3/4 medulloblastomas, we followed the strategy outlined by Körber et al.23 to estimate the model parameters from the measured VAF distribution (code and pseudo-code are available at https://github.com/kokonech/mbOncoAberrations).
Real-time estimate of cell division rate
From the model fits of medulloblastoma initiation and growth to WGS data, we estimated differentiation/loss rates and mutation rates relative to the rate of cell divisions. To convert these estimates to real-time, we used the age distribution at diagnosis for calibration. In a first step, we estimated the cell division rate of UBCPs, \(\lambda \), from the number of generations between gastrulation and MRCA plus the number of generations between MRCA and diagnosis (tD), which can be inferred from the mutational burden in the tumour23. Recall the selective advantage of the growing tumour, \(s\). With λT = sλ, this yields
$$\lambda =\frac1t_\rmD\left(\frac\mathopm\limits^ \sim _\textMRCA\mu +\frac\log N_T(t_\rmD)1-\frac\delta _Ts\lambda \right)=\frac1t_\rmD\left(\frac\mathopm\limits^ \sim _\textMRCA\mu +\frac\log N_T(t_\rmD)\mu \mu _\texteff\right),$$
(9)
where we used the estimate for \(\mu \) from the parameter inference for medulloblastoma initiation and the estimate for the effective mutation rate, \(\mu _\texteff=\frac\mu 1-\frac\delta _Ts\lambda \), from the parameter inference for medulloblastoma growth. Assuming a tumour mass in the order of a few cubic centimetres and hence \(N_\rmT(t_\textD)\,=\,\) 109 cells, and defining \(t_\textD\) as the age at diagnosis, A, plus, on average, 250 d of embryogenesis after gastrulation, we obtained for each tumour (labelled with index i) an estimate for the division rate with mean, \(\langle \lambda _i\rangle =\frac12\langle \mu \rangle (A_i+250\,\rmd)(\langle 2\mathopm\limits^ \sim _\rmM\rmR\rmC\rmA,i\rangle +\log 10^9\langle \mu _\rme\rmf\rmf,i\rangle )\), and standard deviation, \(\sigma (\lambda _i)=\frac12\langle \mu \rangle (A_i+250\,\rmd)\left(\frac2\langle \mathopm\limits^ \sim _\rmM\rmR\rmC\rmA,i\rangle +\log 10^9\langle \mu _\rme\rmf\rmf,i\rangle 2\langle \mu \rangle \sigma \langle 2\mu \rangle +\sigma (2\mathopm\limits^ \sim _\rmM\rmR\rmC\rmA,i)+\sigma (\mu _\rme\rmf\rmf,i)\right)\), in actual time (where the factor 2 accounts for the fact that \(\langle \mu \rangle \) and \(\mathopm\limits^ \sim _\textMRCA,i\) measure the mutation rate and the mutation density, respectively, per haploid genome).
Finally, we computed the mutation rate per day during tumour initiation, by computing \(\mu \lambda _T,i\), with associated uncertainty \(\mu \Delta \lambda _T,i+\lambda _T,i\sigma (\mu )\), which relates the molecular clock to real-time. For this purpose, we averaged across the inferences from all tumours that went into the analysis.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.