Old carbon routed from land to the atmosphere by global river systems

Study approach and methods summary

Our aim was to analyse global-scale patterns of the age and source of river carbon emissions. Radiocarbon studies of river DIC, CO₂ and CH₄ have been conducted from ecological to geochemical perspectives and varying degrees in between. As a result, widely differing sets of variables are available from each study, making river to river comparisons difficult. Here we instead focus on a global approach to compare the ¹⁴C content of river CO₂ emissions and the probable carbon source components within this flux to the atmosphere.

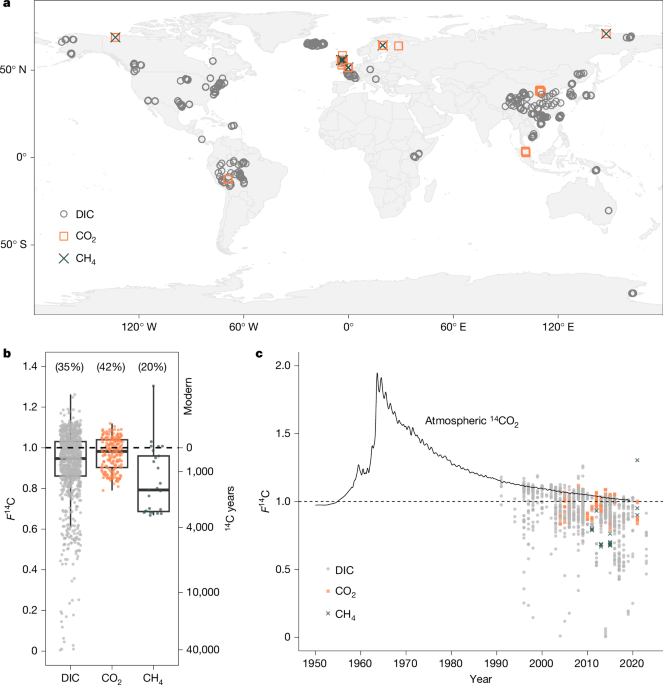
We first assembled a database of measurements of the radiocarbon content of river DIC, CO₂ and CH₄ from the literature and then added a subset of unpublished data. Radiocarbon content is presented here as F¹⁴C. In conventional ¹⁴C dating, F¹⁴C = 1.0 represents 1950 CE; however, in relation to carbon cycling and the atmospheric ¹⁴CO₂ record (Fig. 1c), F¹⁴C < 1.0 indicates carbon older than 1955 CE and F¹⁴C > 1.0 is carbon younger than 1955 CE (Fig. 1b). The database was dominated by DIC measurements, so we demonstrated that DIC and CO₂ are probably in isotopic equilibrium (Supplementary Information section 1), allowing us to explore the F¹⁴C content of global river CO₂ emissions from the database.

Owing to inconsistencies in how catchment characteristics were reported in the literature from which we assembled the radiocarbon measurements (if they were reported at all), we used a global database of hydrological-environmental characteristics (HydroATLAS⁵⁶) to extract key catchment information for each sampling location in a consistent manner (for example, catchment size, lithology, biome).

The resolution limits of HydroATLAS mean that, for catchments <10 km² in size, it was difficult to ensure that the correct catchment characteristics were extracted. Further, not all data in HydroATLAS are available at the catchment scale. For this reason, we extracted data from HydroATLAS at both the reach (1-km radius from the sampling location) and the catchment scale and use the reach characteristics for small catchments ≤10 km² and the catchment characteristics for large catchments >10 km².

We used the HydroATLAS information to explore the potential underlying drivers of the F¹⁴C content of river DIC, CO₂ and CH₄, first through mapping key characteristics such as catchment size, lithology and biome (Fig. 2) and then using a random forest model to explore a wide range of catchment characteristics (such as climate and soil properties). Owing to the catchment size issue identified above, we ran the model separately for catchments ≤10 km² and >10 km² to ensure that we did not incorporate anomalous catchment characteristics into the model.

To determine the potential contributions of different carbon sources, defined here as decadal, millennial and petrogenic carbon sources, we used a two-endmember isotope mixing model with Monte Carlo simulations, constrained by known inputs of petrogenic carbon to river DIC from weathering. To independently assess this approach, we also independently used an unconstrained three-endmember Bayesian isotope mixing model. We then used these estimates of the proportional contribution of different carbon sources to global river DIC to estimate the magnitude of river CO₂ emissions to the atmosphere derived from old carbon (millennial or older).

New data

We include data from three unpublished works in our analysis. These include dissolved CO₂, CH₄ and DIC data from the UK, Taiwan, Cambodia and China.

Eight dissolved CO₂ and three dissolved CH₄ samples were collected for ¹⁴C analysis from a range of urban rivers and canals in London in September 2021. Paired CO₂ and CH₄ samples were collected from the River Brent, Regent’s Canal and the River Thames; CO₂ samples were collected from Bow Creek and more sites on Regent’s Canal and the River Thames (Supplementary Table 1). CO₂ samples were collected using the super headspace method⁵⁷, with samples collected by equilibrating 3 l of water with 1 l of CO₂-free headspace for three minutes and the headspace injected into a molecular sieve cartridge for transport to the National Environmental Isotope Facility (NEIF) Radiocarbon Laboratory in East Kilbride, UK. CH₄ samples were collected with the coiled membrane method²¹, in which water was slowly pumped through a hydrophobic, gas-permeable membrane into a headspace containing ambient air. The vessel was left to collect CH₄ overnight and recovered after 12–18 h; the headspace was collected into foil gas bags and transported by land to the NEIF Radiocarbon Laboratory. CH₄ samples were corrected for the ambient air in the headspace following refs. ^21,52.

River water DIC samples from Taiwanese rivers and the Mekong River in Cambodia were collected using the methods outlined in refs. ^18,58. In Taiwanese rivers, 1-l sampling bottles were submerged into the middle of the channel using a weighted Teflon sampler. On the Mekong River, near-surface samples were collected using a horizontally mounted Niskin-type sampler. River water was then filtered directly into preweighed 1-l foil bags (FlexFoil PLUS) through polyethersulfone filters (0.22 μm) using syringe-mounted filtration, with care to avoid any atmospheric air mixing. The foil bag was filled with approximately 200–500 ml of filtered river water (depending on expected DIC concentration) and then gently squeezed before closing to ensure that no air was trapped. The filled bag was reweighed and stored at 4 °C during fieldwork, before shipping to the UK, in which the sample was frozen within about a week of collection⁵⁸.

The UK, Taiwan and Cambodia samples were processed at the NEIF Radiocarbon Laboratory. CO₂ samples were retrieved from the molecular sieve cartridges by heating to 425 °C. CH₄ samples were passed through soda lime and molecular sieve filters to remove residual CO₂ and then combusted to CO₂ using platinum bead catalyst at 950 °C. For the DIC samples, orthophosphoric acid was added to the defrosted, filtered water sample in the foil bag and the degassed CO₂ collected, isolated and purified using cryogenic traps⁵⁸. The CO₂ for ¹⁴C analysis was then cryogenically recovered and graphitized using Fe–Zn reduction and analysed for ¹⁴C content by Accelerator Mass Spectrometry (AMS) at the Scottish Universities Environmental Research Centre in East Kilbride. For quality assurance, standard materials of known ¹⁴C content were processed alongside the samples.

We collected ¹⁴C samples for DIC from 19 river sites on or draining the Qinghai–Tibet Plateau. Samples were collected in 2017, 2018 and 2023, with five sites visited in both 2018 and 2023 (MD, NQ, TNH, XD and ZMD; Supplementary Table 1). River water samples were filtered to 0.45 μm using polyethersulfone filters and collected in acid-washed (10% HCl v/v, 24 h) 1-l HDPE Nalgene bottles rinsed three times with filtered river water before collection. Samples were kept refrigerated between collections and analysis. DIC was processed to CO₂ for ¹⁴C analysis within 2–3 weeks of collection.

Samples collected in 2017 and 2018 were processed and analysed at the Peking University AMS facility (PKU_AMS) in Beijing, China, following ref. ⁵⁹. Water samples were acidified with phosphoric acid and shaken and heated to 75 °C for 2 h to convert all DIC to CO₂. The CO₂ was then purified cryogenically on a vacuum line and graphitized using zinc reduction. Samples collected in 2023 were processed and analysed at the Beta Lab AMS facility in Miami, Florida, USA. Samples were acidified using phosphoric acid and stripped from the water by bubbling pure N₂ or Ar gas through the sample. The resulting CO₂ was collected cryogenically and graphitized using hydrogen reduction of the CO₂ sample over a cobalt catalyst. In both the PKU and Beta labs, reference standards, internal QA samples and backgrounds were processed alongside the samples.

F
¹⁴C data assembly from the literature

We initially compiled our database using the 209 DIC values available in ref. ¹⁷. We then searched for further studies of river DIC, CO₂ and CH₄ ¹⁴C values from the peer-reviewed literature. We searched and compiled studies published before 2023 using Web of Science and Google Scholar⁶⁰ (Supplementary Fig. 7). The following string terms were used in the search: (dissolved inorganic carbon OR DIC OR carbon dioxide OR CO2 OR methane OR CH4) AND (14C OR radiocarbon) AND (stream OR river); (dissolved inorganic carbon OR DIC OR carbon dioxide OR CO2 OR methane OR CH4) AND (14C OR radiocarbon). We undertook the search several times to ensure completeness. Measurements from groundwater seeps or similar extreme endmembers were excluded, extracting only data from flowing, open water streams and rivers. We augmented these search results with our own knowledge of the literature for which studies were missed in the above searches. Ultimately, we were able to obtain 1,195 observations of fluvial DIC, CO₂ and CH₄ ¹⁴C from 67 studies, including our own data collection outlined above.

From each study, we collected the following information when available (Supplementary Table 1):

• Site identifier (ID)

• Date and year of sample collection

• Brief site description

• Catchment name

• Compound (DIC, CO₂ or CH₄)

• DIC concentration (converted to µmol l⁻¹)

• δ¹³C (‰ VPDB) and associated uncertainty

• δ²H-CH₄ (‰) and associated uncertainty

• Radiocarbon publication code

• Radiocarbon content in F¹⁴C (fraction modern) and Δ¹⁴C (‰) and associated uncertainty

• Radiocarbon age (¹⁴C years) and associated uncertainty

• Sample water pH

• Sample water temperature (°C)

• Latitude and longitude, country and hemisphere of sampling location

• Water type (river, stream and so on)

• Brief method outlines for sample collection and processing

• Exact watershed size (km²)

We then provided flags for the coordinates and data uncertainties collected from the literature.

For the coordinates flags:

• Exact sampling location from the original study

• General but not exact location provided in the original study (for example, centre of catchment)

• Estimated on the basis of the map in the original study in conjunction with Google Earth Pro

For the uncertainty flags:

When data were reported in Δ¹⁴C, we also calculated F¹⁴C and vice versa:

in which λ = 1/8,267 year⁻¹ and y is the year of sample collection.

Some locations in the database were sampled more than once. This is because of a combination of experimental approaches, for example, repeat sampling, exploration of temporal variations and method development. When a sample location was repeat sampled more than four times in a calendar year (that is, more than 0.5% of all observations), we took the average of the F¹⁴C observations at that location for that year and recalculated a new radiocarbon age and uncertainty⁶¹. This removal left n = 1,020 observations (Extended Data Table 1).

Normalization of F
¹⁴C values to atmospheric ¹⁴CO₂

We normalized the F¹⁴C values in the database for each measurement to the F¹⁴C-CO₂ content in the atmosphere in the year of sample collection, defined as F¹⁴C_atm:

in which F¹⁴C_atm is the normalized F¹⁴C value of the sample (Fm_sample in fraction modern) divided by the F¹⁴C value of the atmosphere in the year of sampling (Fm_atmosphere in fraction modern)³⁵.

The atmospheric F¹⁴C-CO₂ values used in equation (3) were compiled from 1950 to 2023. Atmospheric ¹⁴CO₂ is from ref. ³⁴ for 1950 to 2019. For 2020 to 2023, annual ¹⁴CO₂ was estimated by extrapolating the declining annual trend of ¹⁴CO₂ observed between 2014 and 2019. This period was chosen because the curve seemed to be flattening during this period relative to the steeper decline seen earlier in the data (Fig. 1c). Although we note that the relative contributions of contemporary biomass and soil respiration to river carbon emissions are probably not globally consistent and cannot be captured by normalizing to a single year atmospheric ¹⁴CO₂ value, this method allows a consistent normalization of the entire database irrespective of individual river catchment characteristics.

Paired DIC–CO₂
¹⁴C measurements

To explore the relationship between F¹⁴C in DIC and CO₂ emissions, we compiled 15 paired F¹⁴C measurements of DIC and CO₂ (Supplementary Fig. 1, Supplementary Table 3 and Supplementary Information section 2). These paired samples cover 11 distinct sites and a river pH range of 4.2–7.7, indicative of the range of pH found in natural waters. Six of these paired observations come from ref. ¹⁹, collected from two peatland headwater streams, one in north England (Moor House) and one in southern Scotland (Auchencorth Moss). Eight unpublished paired measurements were also obtained from headwater streams in the north of Scotland, four in the Flow Country and four on the Isle of Lewis. Another unpublished paired measurement was obtained from Peru, from the Manu River. Sample ¹⁴C collection and processing for the new Scotland and Peru measurements were the same as for the London, Taiwan and Cambodia samples outlined above.

Data extraction from HydroATLAS

For each data point in the radiocarbon database, we collected information on the catchment characteristics of the sampled river. Unfortunately, this information was reported in a highly inconsistent manner and, in many cases, not at all, in the published literature. Therefore, for consistency in our analysis, we extracted catchment and hydrological characteristics from HydroATLAS⁵⁶. HydroATLAS provides catchment and reach characteristics for rivers across the globe at 15-arcsecond resolution and includes parameters on hydrology, physical catchment settings, climate, land cover and use, soils and geology and anthropogenic influences. We extracted selected parameters at both the reach and catchment scale where possible and added these to our database (Supplementary Tables 1 and 4).

To ensure that we were extracting catchment characteristics for the correct river in HydroATLAS, we collected the details of catchment area for each sampling point from the original study; when this was not available, we estimated catchment size based on indicative values in the original study, published catchment sizes found in other studies of the same rivers or through order of magnitude estimates from visual assessment on Google Earth Pro (for example, 1 km², 10 km², 100 km², 1,000 km² and so on; Supplementary Table 1). Exact catchment sizes and combined exact/estimated catchment sizes are provided separately in the database. We compared the exact or estimated catchment size with the extracted catchment size from HydroATLAS (Supplementary Fig. 6). For most catchments greater than 10 km² in size, the values matched well. For catchments less than 10 km², the relationship broke down because of the resolution of HydroATLAS. For further analysis, we only used reach characteristics (extracted for the nearest river reach within 1 km² of the sampling point) for sampling points with exact or estimated catchment size ≤10 km². For catchments greater than 10 km², we used the catchment characteristics. Note that, for some parameters, only catchment or reach characteristics were available (Supplementary Table 4).

From the catchment size information, we produced two sets of classifications. (1) A binary ‘small’ (≤10 km²) and ‘large’ (>10 km²) classification—this classification was chosen owing to the lower river basin size limit of the HydroATLAS (10 km²) and was based on the exact/estimated catchment size information extracted from the original studies. This binary size class was used primarily for QA/QC checks in the database and also in defining whether to use reach or catchment parameters from HydroATLAS in the random forest model (Extended Data Figs. 3 and 4). (2) A multiclass exponential classification of 0–10 km², 100 km² (10 to 100), 1,000 km² (100 to 1,000) 10,000 km² (1,000 to 10,000) 100,000 km² (10,000 to 100,000), 1,000,000 km² (>100,000)—this classification was based on binary class (1) above for the 0–10-km² class and catchment size extracted from HydroATLAS for the other classes and was used in the analysis presented here. Both size classifications were created manually and are provided in Supplementary Table 1.

From the biomes provided in HydroATLAS, we simplified these into eight classes (Supplementary Fig. 2):

1. 1.

   Temperate grasslands and shrublands, which was the same as HydroATLAS biome ‘8. Temperate Grasslands, Savannas & Shrublands’.

2. 2.

   Tropical grasslands and shrublands, which included HydroATLAS biomes ‘7. Tropical & Subtropical Grasslands, Savannas & Shrublands’ and ‘9. Flooded Grasslands & Savannas’ (which occur mostly in tropical regions⁶²).

3. 3.

   Temperate conifer and boreal forests, which included HydroATLAS biomes ‘5. Temperate Conifer Forests’ and ‘6. Boreal Forests/Taiga’.

4. 4.

   Tropical broadleaf and conifer forests, which included HydroATLAS biomes ‘1. Tropical & Subtropical Moist Broadleaf Forests’, ‘2. Tropical & Subtropical Dry Broadleaf Forests’ and ‘3. Tropical & Subtropical Coniferous Forests’.

5. 5.

   Temperate and Mediterranean broadleaf mixed forest, which included HydroATLAS biomes ‘4. Temperate Broadleaf & Mixed Forests’ (although no samples in the database come from this biome) and ‘12. Mediterranean Forests, Woodlands & Scrub’.

6. 6.

   Tundra, which was the same as HydroATLAS biome ‘11. Tundra’.

7. 7.

   Montane grass and shrubs, which was the same as HydroATLAS biome ‘10. Montane Grasslands & Shrublands’.

8. 8.

   Deserts, which included HydroATLAS biome ‘13. Deserts & Xeric Shrublands’ and also a further classification ‘15. Polar Desert’ added here to include the samples in the database from the Antarctic.

From the lithology classifications provided in HydroATLAS, we simplified these into three classes (Supplementary Fig. 3):

1. 1.

   Metamorphic, which was the same as HydroATLAS class ‘8. Metamorphic Rocks (MT)’.

2. 2.

   Igneous, which included the HydroATLAS classes ‘2. Basic Volcanic Rocks (VB)’, ‘4. Basic Plutonic Rocks (PB)’, ‘7. Acid Volcanic Rocks (VA)’, ‘9. Acid Plutonic Rocks (PA)’, ‘10. Intermediate Volcanic Rocks (VI)’, ‘12. Pyroclastics (PY)’ and ‘13. Intermediate Plutonic Rocks (PI)’.

3. 3.

   Sedimentary, which included the HydroATLAS classes ‘1. Unconsolidated Sediments (SU)’, ‘3. Siliciclastic Sedimentary Rocks (SS)’, ‘5. Mixed Sedimentary Rocks (SM)’ and ‘6. Carbonate Sedimentary Rocks (SC)’.

One data point returned ‘No Data (ND)’ from the HydroATLAS lithology classes and was excluded from the lithology analysis. Data from Antarctica were also excluded from the analysis owing to a lack of lithology data (returning ‘Ice and Glaciers (IG)’ from the HydroATLAS lithology classes).

Statistical analyses

Statistical analyses were carried out in R version 4.1.1 (ref. ⁶³). We used nonparametric Kruskal–Wallis tests with the kruskal.test function in R, supplemented by post hoc analyses consisting of Conover–Iman tests using the conover.test function and unpaired two-sample Wilcoxon tests using the wilcox.test function. We undertook linear regression analyses using the lm function. The details of where each analysis is applied are provided in the Figures in the main text, Extended Data and Supplementary Information.

Random forest model

We explored potential drivers of the age of river carbon emissions using a random forest model. Random forests are a machine learning model that integrate numerous regression trees to make predictions. Owing to its capacity to capture nonlinear relationships, and mitigate the risk of data overfitting, this approach has proved to be successful in numerous environmental studies for unravelling the interplay among variables^64,65,66. In this study, we use random forest models to investigate the relationships between key catchment characteristics extracted from HydroATLAS and F¹⁴C_atm values in the database. We aimed to identify which variables have the strongest control on F¹⁴C_atm of river carbon emissions.

To select the input variables for the model, we first removed variables that correlated significantly with other potential input variables based on a Spearman correlation greater than 0.6 to avoid the results being influenced by correlated input variables. The remaining variables are shown in Supplementary Table 5 and includes the year of sample collection (‘year’).

We split the model runs by catchment size (Extended Data Figs. 3 and 4) using whole catchment characteristics for rivers with catchments greater than 10 km² and reach characteristics for rivers with catchments ≤10 km². Owing to limits on the number of data points, we only applied the model to DIC data, in which observations were n > 100 when separated by size.

We conducted the random forest analysis using the randomForest 4.6-14 package in R (ref. ⁴¹). Random forest models were built for the F¹⁴C_atm-DIC (having removed repeat sampled locations in a calendar year) using all 19 variables from all of the 673 large catchments. We assessed the performance of the random forest model prediction by calculating the coefficient of determination (R_d²) and determining the importance of each variable through the increase in the mean square error. A tenfold cross-validation was used to enhance the robustness of the results. The dataset was randomly divided into ten equal-sized samples, with 90% of the data used for training the random forest model, whereas the remaining 10% was used to assess model performance. This process was iterated ten times until each 10% sample was used and the final model performance was computed as the mean of the ten evaluation results. Following the same approach, random forest models were also built for F¹⁴C_atm-DIC using all 18 variables across all of the 211 small catchments.

We assessed the association between predictor variables and F¹⁴C_atm with partial dependence plots using the pdp R package⁶⁷. The partial dependence plots show how F¹⁴C_atm changes when a given input variable (Supplementary Table 5) varies but all other variables are held constant in the random forest model. We performed the partial dependence analysis ten times (mirroring the ten iterations of random forest models from using tenfold cross-validation) and plotted the mean values from these ten runs, with the variability across the runs indicated by the shaded area (Extended Data Figs. 3 and 4).

Endmember isotope mixing model and Monte Carlo simulation

We used an endmember isotope mixing model and Monte Carlo approach to constrain the role of decadal versus centennial and older carbon inputs to river DIC and its contribution to river CO₂ emissions. To do this, we sought to account for petrogenic inputs from carbonate mineral and rock organic matter weathering and calculate an F¹⁴C value for the non-petrogenic residual. This non-petrogenic residual is a combination of: (1) the DIC supplied from soil or atmospheric CO₂ during carbonate weathering; (2) DIC supplied by silicate mineral weathering from soil or atmospheric CO₂; (3) CO₂ derived from ecosystem respiration and delivered by water flowing through catchments; (4) CO₂ derived from within-river respiration of dissolved and particulate organic carbon by aquatic flora and fauna; and (5) the potential invasion of atmospheric CO₂ if rivers are undersaturated with respect to atmospheric concentrations.

In an ideal world, it would be possible to account for petrogenic inputs to DIC and CO₂ for each watershed in the database (and potentially for each sampling point). To do this, we would need to use dissolved cation (Na⁺, Ca²⁺, Mg²⁺, K⁺) and anion (Cl⁻, SO₄²⁺, Re) data to assess the weathering acids and contributions from carbonate and rock organic matter weathering^18,38,39. Unfortunately, most of the studies reporting river DIC and CO₂ F¹⁴C measurements do not report dissolved ion data, or if they do, do not report the necessary range of cation and anion measurements to complete a weathering-source inversion. As such, we take a global view using our mean F¹⁴C DIC values and assess the petrogenic inputs using global estimates of carbonate and rock organic carbon weathering rates.

We can express total river DIC–CO₂ export as a mass balance of the known lateral and vertical fluxes (concentrations per unit area per unit time):

in which DIC is the sum of dissolved CO₂, HCO₃⁻ and CO₃²⁻ (Supplementary Information section 2), we express all fluxes at the global scale in Pg C year⁻¹ and we assume that carbonate precipitation is negligible at the global scale⁶⁸. Lateral DIC export from rivers to the global oceans is estimated to be 0.52 ± 0.17 Pg C year⁻¹ (ref. ⁴²), and global vertical CO₂ emissions from rivers are estimated to be 2.0 ± 0.2 Pg C year⁻¹ (ref. ⁶), producing a total river DIC flux of 2.5 ± 0.4 Pg C year⁻¹.

We can also express global river F¹⁴C of DIC and CO₂ (F¹⁴C_river) as the mass balance of the three main carbon sources defined in this study, for which the proportional contributions from all three carbon sources (a + b + c) sum to 1:

We can then combine these two mass balances to provide a first-order estimate of the contributions of these sources to the global river DIC flux:

To further constrain equation (6), we account for published estimates of petrogenic DIC inputs to the global river DIC flux derived from weathering of carbonate and rock organic matter. Global carbonate mineral weathering rates are relatively well constrained at an input of 0.15 Pg C year⁻¹ to DIC from petrogenic carbon in the CaCO₃ mineral²². If driven by carbonic acid weathering, this carbon flux is likely to be delivered by hydrological flow paths from weathering zones to streams and rivers. However, if sulfuric acid weathering is operating in landscapes, some of this petrogenic carbon may be released to the atmosphere as CO₂ and not enter the DIC pool⁵³. This fate of carbon is not well constrained globally. Also, rock organic carbon oxidation has been estimated to contribute 0.068 Pg C year⁻¹ in the weathering zone³⁹. Again, it is not known what proportion of this carbon enters the DIC pool^53,69 and may contribute to the global river DIC flux. We thus considered the full range between two scenarios of petrogenic carbon inputs. First, a 0.15 Pg C year⁻¹ scenario, which may represent a lower bound. Second, we consider 0.218 Pg C year⁻¹, which is likely to be an upper bound, summing both carbonate and rock organic matter weathering (we incorporate this as 0.18 ± 0.034 for consistency with other fluxes and uncertainties). Incorporating this ‘weathering input’ flux constraint into equation (6) gives:

Using the mean F¹⁴C value for DIC, CO₂ and CH₄ across all rivers in our database of F¹⁴C_river = 0.919 (Extended Data Table 1) and subtracting petrogenic C inputs (0.150–0.218 Pg C year⁻¹) from the sum of lateral DIC export to the ocean and vertical river CO₂ emissions (2.5 ± 0.4 Pg C year⁻¹), we can simplify equation (7) to:

We can then calculate the non-petrogenic F¹⁴C value (F¹⁴C_{decadal+millennial}), because the petrogenic source is assumed to contain no radiocarbon (that is, F¹⁴C = 0.0). This provided an estimate of the F¹⁴C_{decadal+millennial} = 0.978 to 1.007.

We then assumed that this residual non-petrogenic carbon was a mixture of a decadal-aged carbon source (using mean ± 1σ F¹⁴C content of atmospheric CO₂ between 1950 and 2023, F¹⁴C = 1.226 ± 0.216 (ref. ³⁴)) and a millennial-aged carbon source (using the carbon-weighted mean (±1σ) age of global mineral soil carbon in the upper 0–30 cm, F¹⁴C = 0.841 ± 0.033 (ref. ²⁷)). The conceptual model of this carbon source partitioning, decadal and millennial (and petrogenic; see Bayesian isotope mixing model methods in Supplementary Information section 3), follows refs. ^14,32. The decadal source endmember captures annual to decadal carbon cycling through biomass and soils, including the decomposition of dissolved organic carbon, which tends to have an F¹⁴C value indicative of annual-decadal terrestrial residence times¹⁷. The millennial source endmember captures carbon in soil stores of 0–30 cm depth (and deeper in some regions²⁷), which includes the potential decomposition of older dissolved^14,17,48 and particulate¹² organic matter. To estimate the most probable composition and its uncertainty, we use a Monte Carlo simulation to generate 10,000 model runs, varying the petrogenic flux (0.150–0.218 Pg C year⁻¹) and the F¹⁴C values of the decadal (1.011–1.442) and millennial (0.808–0.874) inputs to equation (8). We report the mean proportional contributions of the decadal and millennial contributions ±1σ of the 10,000 model runs (Extended Data Fig. 5). We then convert these to proportions of the vertical river CO₂ flux by first quantifying the proportional contribution of petrogenic carbon: 0.180 ± 0.034 Pg C year⁻¹ of 2.5 Pg C year⁻¹ (total river DIC flux) = 0.07 ± 0.03 (Table 1) and then subtracting the petrogenic proportion from the total to give 0.93 and multiplying this by the mean decadal and millennial contributions to give 0.41 ± 0.16 and 0.52 ± 0.16, respectively (Table 1). We then multiplied estimated vertical CO₂ emissions from global rivers (2.0 ± 0.2 Pg C year⁻¹) from ref. ⁶ by these proportional carbon source contributions (Table 1). We note that there may be some equilibration of the DIC/CO₂ pool with the atmosphere during river transport and emission, which adds young carbon to the CO₂ pool⁷⁰, meaning that our estimates of old carbon contributions may be conservative.

We were not able to collect consistent, site-specific concentration or emission flux data alongside the F¹⁴C data extracted from the literature. This means that we were not able to scale the F¹⁴C values in the database with local and regional emission fluxes (Supplementary Information section 4).