Observation of an ultra-high-energy cosmic neutrino with KM3NeT

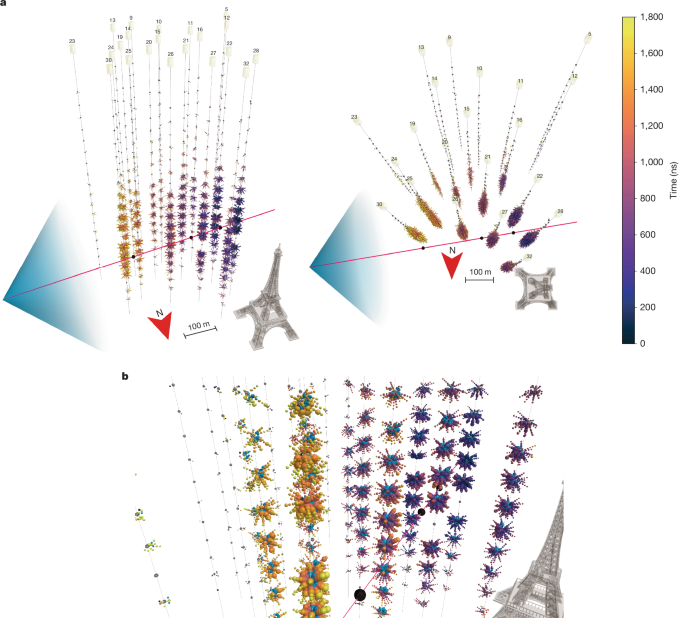
The detector

The KM3NeT detectors⁴ are three-dimensional arrays of photosensors installed at great depths in the Mediterranean Sea. The sensors detect the Cherenkov radiation induced in seawater by relativistic charged particles. They are housed in optical modules⁹, which are 44-cm-diameter pressure-resistant glass spheres, each with 31 3-inch PMTs. Each optical module contains data-acquisition electronics and calibration instrumentation. The modules of the ARCA detector, located at a depth of 3,450 m offshore Portopalo di Capo Passero, Sicily, in the Mediterranean Sea, are chained together in groups of 18, spaced by 36 m, along 700-m-long vertical detection lines anchored to the seabed and kept taut by the buoyancy of the optical modules and top buoys. An electro-optical cable runs along the detection lines, powering the optical modules and transporting data through optical fibres. Detection lines are placed on the seafloor with an average horizontal spacing of 95 m. At the time of the event, the ARCA detector consisted of 21 detection lines. The instrumented volume, that is, the smallest cylinder containing all optical modules, was about 0.15 km³. In its final configuration, the array will comprise 230 detection lines.

The data-acquisition system is based on the ‘all-data-to-shore’ concept: all analogue signals from the PMTs above a certain tunable threshold are digitized offshore and all digital data are sent to shore, where they are processed in real time. The data contain the time stamp of the leading edge and the pulse length of the time-over-threshold signal from a discriminator, jointly referred to as ‘hit’. The time-over-threshold is proportional to the number of converted photoelectrons on the PMT. Although the linear behaviour holds relatively well for pulses up to a few tens of photoelectrons, above 30 photoelectrons, a saturation effect is observed, producing a flattening of the time-over-threshold measurements with increasing charge⁹.

Trigger algorithms search for clusters of hits correlated in space and time. Local coincidences of hits are identified on each optical module within a 25-ns time window. Then, three different clustering algorithms are applied, assuming that hits come from light propagating according to a possible track or shower origin. A space-time coincidence between at least five hits on five modules within 250 m, under the assumption that light expands from a point-like source, constitute a cluster for the nominal shower trigger, allowing for a 25-ns delay to light propagation in water. A similar condition is applied for the track trigger, but this time considering that the light source is a track that moves in the detector at the speed of light in vacuum, and searching for hits in a cylinder of radius 120 m. A low-threshold shower trigger is also applied, requiring coincidences of eight hits on three modules within 110 m. When one or more clusters are found, all data from an \({\mathcal{O}}(10)\text{-}{\mu }{\rm{s}}\) time window are recorded as an event for offline calibration and processing. Triggering criteria are designed to detect events at the lower-energy threshold. In the case of KM3-230213A, 3,659 individual (overlapping) trigger clusters were found in the time window and \({\widehat{N}}_{{\rm{trig}}}^{{\rm{PMT}}}=\mathrm{3,672}\) PMTs participated to form at least one of those trigger clusters. PMTs that have recorded hits but that do not participate in any trigger cluster are predominantly caused by optical backgrounds that are very far away and/or not time-correlated with the physical event. It is for this reason that \({\widehat{N}}_{{\rm{trig}}}^{{\rm{PMT}}}\) is used as observable for the energy estimate.

Data-quality criteria are applied to reject periods with detector instabilities from the analysis sample.

Detector simulation

High-energy neutrino events (100 GeV < E_ν < 100 EeV) were simulated with gSeaGen v7.4.3 (refs. ^48,49), using GENIE⁵⁰ to simulate the neutrino interaction by means of the HEDIS package^51,52. The deep-inelastic scattering model CSMS11 (ref. ⁵³) was used. PROPOSAL⁵⁴ and TAUSIC⁵⁵ were used by gSeaGen to propagate muons and taus up to the detector.

The accurate simulation of the light produced by a muon of a given energy is crucial to the muon energy estimate. KM3NeT uses proprietary code, which simulates the continuous and stochastic energy losses owing to bremsstrahlung, pair production, photonuclear interactions, delta rays and ionization, as well as the multiple Coulomb scattering and deep-inelastic scattering. Differential cross-sections for the main processes are extracted from refs. ^56,57. The light produced by the muon and the secondary particles is simulated by sampling photon tables that contain the probability density functions of the arrival time of Cherenkov light on a PMT as a function of the distance from the emission point and the PMT orientation with respect to the particle⁵⁸. For secondary particles, equivalent tabulated values for electromagnetic shower light are used. The amount of photons generated depends on the type and energy of the particle and has been adjusted according to Geant4 simulations⁵⁹.

The photon tables account for light absorption, scattering and chromatic dispersion. Absorption is modelled on the basis of in situ measurements¹⁴; the scattering model for seawater accounts for pure-water scattering, following the Einstein and Smoluchowski description^60,61, and particle scattering, accounting for the wavelength dependence using the Kopelevich parameterization⁶² and considering the Petzold data⁶³ for the angular dependence. The angular acceptance and average quantum efficiency of the PMTs are also accounted for in the tables, as derived from detailed simulations of the PMT and the structure of the optical module⁶⁴, and from laboratory measurements⁶⁵.

The simulation of the stochastic energy losses has been cross-checked by comparing the total simulated amount of energy lost by the muon over a given distance with the same quantity computed using the PROPOSAL software⁵⁴. Agreement at better than the 10% level was found over the whole energy range of interest. Moreover, PROPOSAL has also been used to check that varying the theoretical models used to describe energy losses^66,67,68,69 yields differences that are within the stochastic fluctuations of the energy-loss processes.

Because no external data are available in this energy range to validate the simulation procedure, the particle-propagation and light-simulation code has also been compared with state-of-the-art Geant4-based⁵⁹ simulation and with a custom GPU-based photon-tracking code (https://github.com/PLEnuM-group/PhotonPropagation.jl) in which the same water model and detector response have been implemented in an independent way. The output of these simulations are in good agreement; when using the alternative simulations for the energy measurement, the result is within 10% of the nominal value.

After light simulation, the readout is simulated. The conversion from photoelectrons on the cathode of the PMT to a time-over-threshold measurement and the transit-time distributions of the PMTs reproduce laboratory measurements⁶⁵. The gain, gain spread and relative PMT efficiencies come from in situ measurements⁷⁰. Afterpulses in the PMTs are at present not simulated. Optical background rates and the status of each PMT in the detector are simulated using the rates measured in the detector, following the run-by-run approach pioneered by the ANTARES Collaboration^71,72. Subsequently, the simulated data are subjected to the same trigger and reconstruction algorithms that are applied to the data. Comparisons between data and Monte Carlo simulations are provided in Extended Data Fig. 1 for a loose event selection in which the sample is dominated by atmospheric muons. Wrongly reconstructed atmospheric muons that appear as upgoing events in the zenith distribution are completely removed once the selection on the reconstruction log-likelihood is applied.

Event reconstruction

The directional reconstruction of the muon track is performed with the standard algorithm, which is based on the arrival time of the Cherenkov photons at the PMTs⁷³. Under the hypothesis that a muon travelling in direction \(\overrightarrow{d}\) is at position \({\overrightarrow{p}}_{0}\) at time t₀, the arrival time of the Cherenkov light at position \(\overrightarrow{q}\) is

in which D is the distance of closest approach of the muon to \(\overrightarrow{q}\) and z is the distance the muon travels before emitting a photon under angle θ_C, \(z=\overrightarrow{d}\cdot (\overrightarrow{q}-\overrightarrow{{p}_{0}})-\frac{D}{\tan {\theta }_{{\rm{C}}}}\); v_g is the group velocity of light at a reference wavelength of 460 nm.

The reconstruction algorithm maximizes the likelihood of the arrival time residuals

in which p denotes the probability density function of the arrival time residual r_i, obtained from interpolated photon tables, at a distance d_i from the emission point. The angles ϕ_i and θ_i describe the orientation of the PMT with respect to the track direction. The photon tables are the same as those that have been described above for the simulation of light from the muon trajectory. They include the contribution of optical background.

The algorithm uses only the first hit on each PMT, as they carry most of the information on the muon direction. As a result of this choice, the reconstruction is robust against PMT afterpulses and other details of modelling of later hits. For the likelihood maximization, only the first hits in a cylinder of radius 175 m and axis defined by the prefit direction are used. This is the standard setting, which was chosen as it optimizes the speed of the algorithm. In the case of KM3-230213A, there are hits outside this cylinder, but it was tested that including them alters the reconstructed track by less than the statistical uncertainty on the direction.

To mitigate the effect of local minima on the likelihood function, the maximization is preceded by a prefit, scanning in 4π sr over assumed track directions. This procedure generates a set of starting points for the likelihood maximization. The track with the largest likelihood is retained.

For ascertaining the quality of the events, the log-likelihood ratio, \(\log ({{\mathcal{L}}/{\mathcal{L}}}_{{\rm{b}}})\) is used, with \({{\mathcal{L}}}_{{\rm{b}}}\) the likelihood computed for the case of only optical background hits. This quantity effectively quantifies the number of hits whose arrival time matches the expectation from the track hypothesis. Typical well-reconstructed muons have a value ≳50, with a tail of larger values resulting from well-reconstructed events with many hits. KM3-230213A has a log-likelihood ratio of 1,415.2, which is the highest value observed in the 21-line ARCA data.

To illustrate the quality of the reconstruction, Extended Data Fig. 2 presents the photon arrival time residuals, which represent the difference between the measured time and the expected time from the reconstructed muon trajectory hypothesis, shown here for the first hits on the PMTs. Many hits are compatible with the muon hypothesis with nanosecond accuracy, even for PMTs located far from the track. Hits arriving after the main peak are because of photons that have scattered in the water and/or that were emitted under some angle other than θ_C from the muon track. These contributions are accounted for in the reconstruction and the large log-likelihood ratio value reflects the agreement of these residuals with the detailed expectation.

Pointing of the telescope

The directional uncertainty on the event is dominated by uncertainty on the absolute orientation of the detector on Earth.

Compasses and accelerometers in the optical modules allow for an estimation of their orientation. The detection lines move with the sea current, which can displace the top modules by \({\mathcal{O}}(10)\,{\rm{m}}\). The continuous monitoring of the optical module positions is therefore mandatory. For this purpose, a system of autonomous acoustic emitters is used, located in and up to 1 km outside the detector on the seabed⁷⁴. The acoustic signals are recorded by piezoelectric sensors in the optical modules. A χ² fit of the arrival times of the sound is used to determine the orientation and shape of the detection line as parameterized by a mechanical model. In this way, the relative positions of the optical modules can be determined to within 0.15 m. Acoustic signals are processed at 10-min intervals; the results of the fit are interpolated to provide the relative positions of the optical modules over time⁷⁵. At the time of the event, the string tilts changed steadily by about 2° over a time span of 2 h, corresponding to less than 0.1° in 10 min. The uncertainty on the position of the detector elements owing to the interpolation of the acoustic data is thus negligible.

The acoustic system measures distances between the optical modules and acoustic emitters but this does not constrain the absolute orientation of the telescope on Earth. During sea campaigns, the positions of the detection lines and acoustic emitters are measured. The emitter positions are used to determine the nominal absolute orientation. These data are at a present accurate to approximately 10 m. This is supported by comparisons with two bathymetry datasets (for the vertical positions) and internal cross-checks with the acoustic system (for the horizontal positions). The position uncertainty translates, after conservatively rounding the result, to an uncertainty of 1° on rotations of the detector around each of the three axes.

An independent cross-check of the pointing was performed by means of a measurement of the directional deficit of atmospheric muons owing to the absorption of cosmic rays in the Moon, similar to ref. ⁷⁶. This anti-signal of the Moon was studied in 335 days of data when the detector consisted of 19 and 21 detection lines. The Moon shadow signal was found at a significance of 3.2σ. In evaluating the Moon shadow for different assumed rotations around the vertical axis, in the range ±3° in steps of 0.25°, the largest significance was found for the nominal orientation. The corresponding uncertainty is evaluated by means of simulations to 0.24°.

A comparison of detector-line depths determined with the acoustic system and the two bathymetry datasets yields further evidence that the system is aligned to within 1°.

Propagating the 1° uncertainty to the celestial coordinates of the event yields a circular 68% confidence region on the sky with a radius of 1.5°. This uncertainty is the dominant source of (systematic) uncertainty in the determination of the celestial coordinates of KM3-230213A.

Simulations of muons in the same location as KM3-230213A were performed at energies from 1 to 1,000 PeV to evaluate the statistical uncertainty on the direction estimation. At 100 PeV, 50% (90%) of the muons are reconstructed within 0.12° (0.28°) from the nominal direction. The azimuthal uncertainty increases with energy, so that, for an energy of 500 PeV, 50% (90%) of the muons were reconstructed within 0.17° (0.38°). These uncertainties are negligible with respect to the 1.5° 68% confidence region and are mentioned here only to indicate the future potential of a fully aligned detector.

We foresee upgrading the detector in the next sea campaign by using new acoustic emitters whose absolute position will be measured with <1-m accuracy in each direction. This, as well as the extra collected data for the Moon shadow analysis, will allow for a recalibration of the data and a more precise determination of the celestial origin of KM3-230213A.

Energy estimate

The energy of a muon above a few TeV can be estimated by measuring its energy loss. Radiative energy losses produce showers of charged particles along the muon trajectory that induce excess Cherenkov photons along the track. The photons arrive on the PMTs very close in time, producing a large number of photoelectrons that translate into hits with a large time-over-threshold. In the case of KM3-230213A, the large number of photons induced by the muon saturates most of the PMTs within about 100 m from the track, and hits are recorded even up to a distance of 300 m. This saturation effect is visible in more than 25% of the PMTs that participated in the triggering of KM3-230213A and is reproduced in simulations. Several subsequent hits are observed on the PMTs and at least some of them could be attributed to afterpulses, which are not modelled in the Monte Carlo simulations. The number of PMTs that participate in the triggering of the event, \({{\mathcal{N}}}_{{\rm{trig}}}^{{\rm{PMT}}}\), is used as an observable in the energy estimation to overcome this possible issue. This observable does not exploit the full information from the event, as it does not account for the time-over-threshold information, but is robust against the limitations of the simulations because PMTs are only counted once if several hits are recorded.

Simulations of muons of various energies traversing the detector in the same direction and location as the reconstructed event were used to estimate the energy of KM3-230213A. The optical properties of water (scattering and absorption lengths) and the detection efficiency of the optical modules were varied in the simulation to account for systematic uncertainties, within the known limits for these parameters. The estimate of the muon energy E_μ is derived from the likelihood \({\mathcal{L}}({E}_{{\rm{\mu }}},\overrightarrow{\xi }\,;{{\mathcal{N}}}_{{\rm{trig}}}^{{\rm{PMT}}})\), in which \(\overrightarrow{\xi }\) are nuisance parameters that affect the \({{\mathcal{N}}}_{{\rm{trig}}}^{{\rm{PMT}}}\) distribution. The likelihood \({\mathcal{L}}\) is estimated from the aforementioned Monte Carlo simulations at discrete combinations of E_μ and the three nuisance parameters. A Gaussian term is added to the likelihood to constrain each of the nuisance parameters to within 10% (1σ) of the nominal value. The energy estimate is the value that maximizes the constrained likelihood. The maximum-likelihood values for given \({{\mathcal{N}}}_{{\rm{trig}}}^{{\rm{PMT}}}\) are shown in Extended Data Fig. 3 left, with the 68% confidence level interval with and without systematic uncertainties, computed from Wilks’ theorem¹³. The log-likelihood profile for \({\widehat{{\mathcal{N}}}}_{{\rm{trig}}}^{{\rm{PMT}}}=\mathrm{3,672}\) is shown in the right panel of Extended Data Fig. 3, with the 1σ, 2σ and 3σ confidence levels, with and without systematics.

Scattering of light does not influence the energy estimate by more than several percent. Similarly, it was found that the optical module efficiency has a <10% level effect on this estimation. The most relevant effect comes from light absorption: a +10% (−10%) modification of the absorption length yields a −0.21 (+0.25) shift in the logarithm of the estimated energy. Finally, it was checked that modifying the muon direction and location in the simulations, within the estimated systematic uncertainties from the detector calibration, does not affect the energy measurement.

The incoming neutrino energy is estimated using Monte Carlo simulations in which neutrino interactions are simulated over a large volume surrounding the detector. Because the neutrino interaction point is unknown, a flat prior is assumed on the muon propagation length in case the interaction occurred in the sensitive volume of the detector, up to 350 m away from the instrumented volume. If instead the interaction occurred outside the sensitive volume, the muon propagation distance distribution is taken from the large-scale Monte Carlo productions obtained with the standard KM3NeT simulation chain. Neutrino events are weighted according to a power-law spectrum with a spectral index equal to −2 to finally estimate the neutrino energy distribution that would produce muons at the detector distributed according to the energy estimate and its uncertainty.

Background evaluation

Atmospheric muons from cosmic-ray extensive air showers constitute most of the events reconstructed in neutrino telescopes. The probability that KM3-230213A is an atmospheric muon is constrained from its reconstructed direction and energy. The muon flux drops rapidly with energy; given that the primary flux of ultra-high-energy cosmic rays extends up to at most several hundred EeV (refs. ^77,78), muons at sea level cannot exceed an energy of few tens of EeV, as muons carry on average around 10% of the primary energy. However, the flux of atmospheric muons at high energies is affected by several uncertainties, such as those on the flux and spectrum of primary cosmic rays, on the composition of this flux, on the hadronic interactions of cosmic rays and of their interaction products. For this reason, a conservative estimate of the surviving muon background has been obtained using a toy model in which several muons have been injected on the surface of the sea according to a power-law spectrum with spectral index −2.7 and normalization at 100 PeV equal to 10⁻¹⁷ GeV cm⁻² s⁻¹ sr⁻¹. These assumptions yield an overestimation of the muon flux by at least one order of magnitude over the whole energy range of interest, so that a conservative estimate of the rate of muons reaching the detector can be obtained.

Muons in the EeV range and beyond have a maximal range of about 60 km in water. Requiring that they must reach the detector still with at least an energy of 10 PeV reduces their effective range to about 30 km. Given the curvature of the Earth and the measured zenith angle, a muon should have entered the water at a distance of approximately 140 km from the detector. The direction of the event points towards the Malta Escarpment, a cliff rising above the abyssal plain: an atmospheric muon travelling in this direction should cross it to reach the detector. In Extended Data Fig. 4, bathymetric data have been used to show the path travelled by a particle along the reconstructed direction. Assuming an average density of 2.6 g cm⁻³ for rock in the seabed, the total amount of matter to be traversed is then on the order of 300 km water-equivalent for the reconstructed direction and becomes smaller than 60 km only if the absolute orientation of the detector is wrong by more than 2° in zenith.

Even assuming a flux that overshoots by one order of magnitude the total flux of atmospheric muons, and including the uncertainties on the zenith angle reconstruction for KM3-230213A, the upper limit on the muon rate is ≪10⁻¹⁰ events per year when assuming a direction within 2σ of the best-fit value. For a mis-reconstruction at a 5σ level error, the upper limit is still ≪10⁻⁴ events per year for the single-muon hypothesis and ≪10⁻³ events per year for muon bundles of low multiplicity in which only a few parallel muons from the same cosmic-ray air shower could reach the detector. This estimation is confirmed when extrapolating the expected rate of events from Monte Carlo simulations¹⁶ accounting for muon absorption in water following ref. ⁷⁹.

Bundles of downgoing (zenith angles smaller than 60°) atmospheric muons, or muons from simultaneous but unrelated cosmic-ray air showers, can produce a large amount of light in the detector. Such events could be mis-reconstructed as a horizontal track. Such coincidences would, however, not have good hit-residuals distributions on all PMTs over many detection lines, in contrast to what is observed for KM3-230213A. This is further corroborated by the detection of several showers along the muon path and their collinearity (as shown in the Supplementary Material): given the good time resolution of the detector elements, a nanosecond-level temporal coincidence between the arrival time of muons at the detector and the emission of showers along their track would be needed to create such a light pattern in the detector, which is extremely unlikely.

Considering the reconstructed arrival direction, neutrinos from cosmic-ray interactions in the atmosphere are not substantially absorbed at least up to some tens of EeV. However, the flux of these atmospheric neutrinos falls steeply with energy. The conventional component, arising from pion and kaon decays in the cosmic-ray extensive air shower, fades away at an energy of about 100 TeV–1 PeV. In that energy range, a prompt component is expected to arise from the decay of short-lived charmed hadrons and become the dominant contribution to the atmospheric flux. Reference neutrino conventional and prompt fluxes were computed using the MCEq software⁸⁰ and the Sibyll 2.3c hadronic interaction model⁸¹, for the location of the ARCA detector: the expected event rates above 100 PeV in the detector are on the order of (1–5) × 10⁻⁵ events per year, depending on the chosen model of the primary cosmic-ray flux⁸². Estimations of prompt fluxes are affected by large uncertainties⁸³; even considering the most optimistic estimations, the event rate from prompt atmospheric neutrinos is less 5 × 10⁻³ events per year. An alternative possibility could be that the detected muon does not come from the interaction of a ν_μ from the prompt component but rather arises from the decay of a tau lepton from the prompt atmospheric ν_τ flux. The branching ratio of charmed hadrons to ν_τ is about a tenth of that to muon neutrinos, hence the expected flux in the atmosphere is one order of magnitude lower. However, above EeV energies, the tau decay length (>50 km) increases the effective volume for the detection of these neutrino interactions. Nonetheless, the prompt flux still remains too low to explain the observed event, with an estimated event rate from atmospheric prompt tau neutrinos ≤10⁻⁵ events per year for the flux estimated with the Sibyll 2.3c hadronic interaction model.

Search for point-like neutrino sources

Data of different configurations of the ARCA and ORCA detectors, as well as the public data of the ANTARES and IceCube experiments, have been analysed to evaluate a possible directional excess of neutrinos close to KM3-230213A. Details on the analysed datasets and respective analysis methods are given in Extended Data Table 1. Depending on the available frameworks, either an ON/OFF method or a maximum-likelihood approach (binned or unbinned) was used. In the latter case, the inspected region was divided into pixels covering equal areas (about 0.1° × 0.1°) in solid angle by using the HEALPix tool⁸⁴ with a value of N_side parameter of 512 and the likelihood was maximized in each pixel. The results are summarized in Extended Data Table 2.

Searches for counterpart candidates

Four selection methods have been applied to astronomical catalogues to build a counterpart blazar candidate sample. The searches were performed within 3° from KM3-230213A (99% event error region).

Method 1. Archival wavelength data were used to pinpoint a blazar counterpart: X-ray sources from the first eROSITA catalogue²² were cross-matched with the radio NVSS catalogue²⁴, selecting 18 sources with radio flux greater than 10 mJy. Infrared data collected by WISE²³ were used to further refine the list of possible counterparts. Blazars populating the ‘WISE blazar strip’⁸⁵ were selected, narrowing the list of candidate blazars to seven objects.

Method 2. Following the approach suggested in ref. ⁸⁶, measurements from Very Long Baseline Interferometry (VLBI) from the Radio Fundamental Catalog (RFC 2024b (https://astrogeo.org/rfc/)) were used. All sources above its present completeness cutoff of 100 mJy at 8 GHz were selected, resulting in five objects with median VLBI flux density ranging from 0.1 to greater than 2 Jy, as in Extended Data Table 3.

Method 3. The Roma-BZCAT²⁵ has been used to search for active galactic nuclei correlations. This blazar catalogue contains 3,561 sources, compiling the results of multifrequency observations. Three blazars were found in this catalogue.

Method 4. The 4FGL-DR4 catalogue¹⁷ is the latest compilation of gamma-ray sources observed by the Fermi-LAT instrument in 14 years of survey data in the 50 MeV–1 TeV energy range: four sources were selected.

The main properties of the selected sources and the respective selection method(s) are described in Extended Data Table 3.

Exposure and tension computation

The KM3NeT/ARCA all-sky exposure is defined as:

in which T^KM3NeT = 335 days (covering the 19 and 21 detection line configurations of ARCA) and \({A}_{{\rm{eff}}}^{{\rm{KM3NeT}}}\) is the sky-averaged effective area, shown in Extended Data Fig. 5, averaged between neutrinos and antineutrinos. This effective area has been estimated for the track selection described in the text (\({{\mathcal{N}}}_{{\rm{trig}}}^{{\rm{PMT}}} > \mathrm{1,500}\), track length longer than 250 m and track-reconstruction log-likelihood ratio larger than 500). The expected number of events for a per-flavour \(\nu +\bar{\nu }\) all-sky flux Φ is then simply:

in which the integration bounds are fixed to the central 90% neutrino energy range associated with KM3-230213A.

The all-sky exposures \({{\mathcal{E}}}^{{\rm{Auger}}}(E)\) and \({{\mathcal{E}}}^{{\rm{IceCube}}}(E)\), averaged between neutrinos and antineutrinos, have been estimated using published material. The effective area of the Pierre Auger Observatory was taken from the data release from ref. ⁸⁷, for the three analysis samples (Earth-skimming, low-zenith downward-going, high-zenith downward-going), with a livetime of 18 years. The IceCube/EHE all-flavour effective area was taken from the 9-year analysis sample⁸⁸.

Assuming a per-flavour single-power-law diffuse neutrino flux Φ(E) = ϕ(E(GeV))⁻², we may estimate the most probable flux normalization \(\widehat{\phi }\) given one observed event in KM3NeT and zero events in Auger and IceCube/EHE samples, using a maximum-likelihood estimator with Poisson likelihoods: \(\widehat{\phi }=7.5\times 1{0}^{-10}\,{\text{GeV cm}}^{-2}\,{{\rm{s}}}^{-1}\,{{\rm{sr}}}^{-1}\).

For such a flux, 0.59 and 0.40 events would be expected in IceCube and Auger, respectively, which is compatible with their null observations. The corresponding expected number of events in KM3NeT is about 0.013 events, hence hinting at a 2.2σ upward fluctuation. The joint Poisson probability of such a configuration (one event in KM3NeT and zero in IceCube and Auger) is about 0.5% (2.6σ).

Inclusion & ethics statement

The scientific objectives of the KM3NeT Collaboration are the search for and observation of sources in the Universe of high-energy cosmic neutrinos and the measurement of characteristics of neutrinos generated in the Earth’s atmosphere. For this, the Collaboration is building a network of neutrino detectors at the bottom of the Mediterranean Sea. At the same locations, the network also provides nodes for the connection of instruments for Earth and sea science studies. Building the detectors with instrumented volumes of up to several cubic kilometres will take several years. Scientific analyses of the recorded data are conducted under the supervision of the Collaboration; after several years, the data will be made available to others as described in the KM3NeT data dissemination plan.

The scientists and engineers in the KM3NeT Collaboration that have come together because they share the scientific interest and come from different backgrounds, cultures and countries. This diversity is considered a strength of the Collaboration and a basis for high-quality research. To nurture the diversity, the Collaboration has developed a code of conduct and ethical behaviour built on a set of shared values and describing rules of good conduct.

The formal rules for the Collaboration are described in a Memorandum of Understanding (MoU) signed by the funding authorities of the institutes employing the individuals participating in the KM3NeT Collaboration.