Multimodal cell maps as a foundation for structural and functional genomics

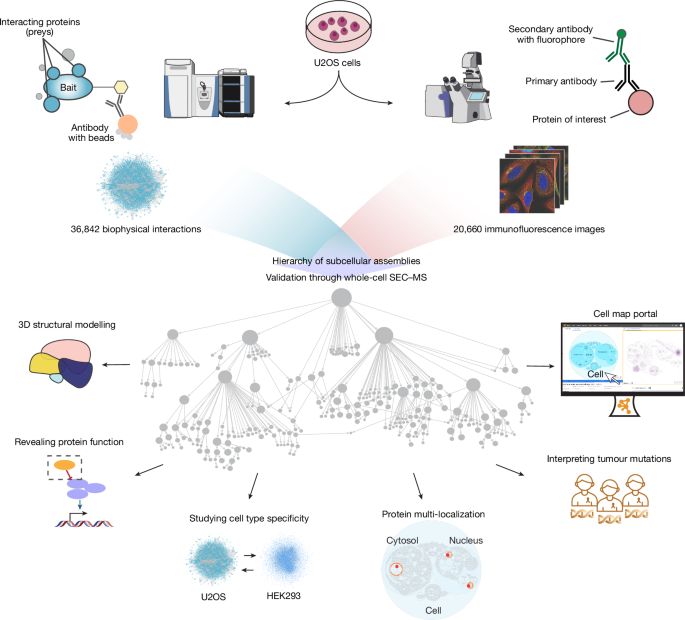
AP–MS data collection

U2OS cell cultures were processed for protein–protein physical interaction mapping by AP–MS, according to a previously described protocol developed as part of the BioPlex project¹⁴. U2OS cells were obtained from American Type Culture Collection (ATCC) and tested for Mycoplasma contamination. C-terminal HA-Flag-tagged DNA constructs targeting each of 2,174 bait proteins were constructed using clones from the human ORFeome library⁵⁷ and introduced into U2OS cells by lentiviral transfection. Baits were selected based on success in previous pull-down experiments and to ensure broad sampling of the interactome as observed previously²². Immobilized and pre-washed mouse monoclonal anti-HA agarose resin was incubated with cell lysates to extract protein baits and their associated protein complexes. Subsequently, these were eluted with HA peptide then reduced and digested with trypsin. Approximately 1 µg of peptide was loaded for reversed-phase liquid chromatography with a C18 microcapillary column followed by tandem MS (Thermo Fisher Q-Exactive HFX) using data-dependent acquisition selecting the top 20 precursors for MS2 analysis. Proteins were identified from the MS2 spectra using Sequest⁵⁸, filtered to 1% protein-level FDR with additional entropy-based filtering¹⁴. The CompPASS algorithm^59,60 was used to select high-confidence (top 2%) protein–protein interactions on the basis of the abundance of proteins in each immunoprecipitation compared with their average levels across all other immunoprecipitations. Interactions were further filtered with CompPASS-Plus at a 1% FDR^14,61. Steps for quality control were as follows. Clones were sequence-validated as described previously⁵⁷. AP–MS analyses required the bait protein to be detected in the Sequest results; moreover, bait proteins were required to have a higher abundance (based on spectral counting) in their own pull-down compared with the other pull-downs on the same 96-well plate. To remove under-loaded samples, we required LC–MS runs to contain a minimum of around 5,000 PSMs and about 700 proteins. Enrichment of interactions within CORUM complexes (Extended Data Fig. 1c,d; CORUM v.4.1) was computed using a one-sided binomial test, assuming background probability of interaction equal to the network’s interaction density, with Benjamini–Hochberg (BH) FDR correction. CORUM complexes for each case were limited to those with at least three proteins and at least one AP–MS bait in the network. Randomized networks were constructed preserving the overall number of interactions per bait (node degrees).

Matched protein IF imaging data

U2OS cell cultures were analysed using IF confocal imaging as part of the Human Protein Atlas project (HPA) using a previously described protocol¹². U2OS cells were obtained from ATCC and were authenticated according to the manufacturer using morphology, karyotyping and PCR-based approaches to confirm the identity and to exclude intraspecies and interspecies contaminations. U2OS cells were seeded in 96-well glass-bottom plates and grown to a confluence of 60 to 70% at 37 °C in McCoy 5A medium, supplemented with 10% fetal bovine serum (FBS) and 5% CO₂ for propagation. Cells were then fixed in 4% paraformaldehyde followed by permeabilization with Triton X-100 detergent and incubated with the HPA primary antibody for the target protein, overnight at 4 °C. HPA antibodies were diluted to 2–4 μg ml⁻¹ in blocking buffer with 1 μg ml⁻¹ mouse anti-tubulin and 1 μg ml⁻¹ chicken anti-calreticulin. The next day, cells were incubated at 90 min at room temperature with secondary antibodies (goat anti-rabbit AlexaFluor 488; goat anti-mouse and goat anti-chicken AlexaFluor 647; or goat anti-rat AlexaFluor 647) diluted to 1 μg ml⁻¹ and counterstained with 4′,6-diamidino-2-phenylindole (DAPI). IF images were acquired using a Leica SP5 confocal microscope equipped with a ×63 HCX PL APO 1.40 oil CS objective. Each IF image contains four colour channels, one for the protein of interest and the other three channels for reference markers corresponding to nucleus (DAPI), microtubule (anti-tubulin antibody) and endoplasmic reticulum (anti-calreticulin antibody). Antibody quality was scored according to a standard HPA protocol (https://www.proteinatlas.org/about/antibody+validation); the highest scoring antibody per protein was selected with up to two technical replicate images.

SEC–MS data collection

We collected a proteomic SEC–MS dataset in the U2OS cell line according to a previously described procedure⁶². U2OS cells were tested for Mycoplasma contamination. Three 15 cm dishes of confluent U2OS cells for each replicate (n = 3) were washed and collected in ice-cold SEC buffer (50 mM KCl, 50 mM NaCH₃COO, 50 mM Tris, pH 7.2, containing 1× EDTA-free HALT protease and Thermo Fisher Scientific phosphatase inhibitor cocktail). These samples were subjected to a fractionation protocol described previously⁶³, with modifications. In brief, cells were lysed using a Dounce homogenizer with a tight pestle for 3.5 min on ice. Lysates were ultracentrifuged at 100,000 rcf for 15 min at 4 °C, and the supernatants were concentrated over 100 kDa molecular mass cut-off spin columns (Sartorius). A standard Bradford assay was performed to inject 600 µg of protein for each replicate into a single 300 × 7.8 mm BioSep-4000 column (Phenomenex) using SEC buffer without protease inhibitors. The samples were then separated into 40 fractions at 15 s per fraction using the 1290 Series semi-preparative HPLC (Agilent Technologies) system at a flow rate of 0.6 ml min⁻¹ at 6 °C. The collection end point was predetermined by measuring the end of the BSA standard peak, discarding anything smaller than a single BSA protein size. The resulting fraction volumes of protein were denatured by adding to a final concentration 20% (v/v) 2,2,2-trifluoroethanol (Sigma-Aldrich), reduced and alkylated⁶⁴. Subsequently, we added an equal volume of 50 mM ammonium bicarbonate for overnight digestion with trypsin (New England Biolabs) at 37 °C. The resulting peptides were cleaned with C-18 STop And Go Extraction (STAGE) tips⁶⁵ using 40% (v/v) acetonitrile and 0.1% (v/v) formic acid in water as the elution buffer. Peptide concentrations were measured on a NanoDrop One instrument (Thermo Fisher Scientific, 205 nm, Scopes method), after which we loaded approximately 50 ng of peptides onto the TimsTOF Pro2 (Bruker Daltonics) system with CaptiveSpray source coupled to a nanoElute UHPLC (Bruker Daltonics) device using an Aurora Series Gen2 analytical column (25 cm × 75 μm, 1.6 μm FSC C18; Ion Opticks). The instrument was set to acquire in DIA-PASEF mode as previously outlined⁶⁶. The sample batch was randomized before injection. Acquired SEC–MS data were searched on DIA-NN (v.1.8.1.0)⁶⁷ against the UniProt human sequences (UP000005640, downloaded 2 June 2023) and common contaminant sequences (229 sequences). Library-free search was enabled, using trypsin/P protease specificity and 1 missed cleavages. Other search parameters included 1 maximum number of variable modifications, N-terminal M excision, carbamidomethylation of C and oxidation of M. Peptide length ranged from 7 to 30, precursor charge ranged from 1–4, precursor m/z ranged from 300 to 1,800, and fragment ion m/z ranged from 200 to 1,800. Precursor FDR was set to 1%, with 0 for settings ‘mass accuracy’, ‘MS1 accuracy’ and ‘scan window’. The settings ‘heuristic protein inference’, ‘use isotopologues’, ‘match between run (MBR)’ and ‘no shared spectra’ were all enabled. ‘Protein name from FASTA’ was chosen for the protein inference parameter along with ‘double-pass mode’ for neural network classifier. Robust LC (high precision) was used for the quantification strategy, RT-dependent mode for cross-run normalization, and smart profiling mode for library generation. Analyses of SEC–MS data used the protein elution profiles, defined as the protein-level quantification values reported by DIA-NN across all fractions. The similarity was calculated between the elution profiles for every pair of proteins, taking the mean Pearson correlation across the three replicates. For assessment of reproducibility across biological measurements (Extended Data Fig. 5b), we first selected the set of proteins present in all three replicates (n = 5,018). For each replicate, we determined each protein’s elution pattern, defined as the set of Pearson correlations between that protein and every other of the 5,018 proteins. We then calculated the Pearson correlation of protein elution patterns across replicates for the same protein or, alternatively, between random pairs of proteins.

AP–MS and IF data preprocessing

Proteins were first pre-processed within the AP–MS and IF modalities separately. For the AP–MS data, the node2vec⁶⁸ Python3 implementation (https://github.com/eliorc/node2vec) was used to represent each protein i as a 1,024-dimension feature vector (x_i) based on its protein–protein interaction neighbourhood (p = 2, q = 1, walk length = 80, number of walks = 10). For the IF data, we applied DenseNet-121, a convolutional neural network pre-trained for object recognition in protein IF confocal images⁶⁹. DenseNet-121 was used to represent each protein as a 1,024-dimension feature vector (y_i) from the four channels of the colour image.

Multimodal embedding overview

We developed a self-supervised multimodal machine learning model to integrate (co-embed) the AP–MS and IF protein representations into a single low-dimensional (128-dimension) embedding space (Extended Data Fig. 2a). Our model is based on the autoencoder architecture known as multimodal structured embedding⁷⁰ with modifications. Parameters of the autoencoder are trained using a two-component loss function that combines reconstruction loss and triplet (contrastive) loss. Details are provided in the ‘Encoder/decoder architecture’, ‘Loss functions’ and ‘Model training’ sections below.

Encoder/decoder architecture

The separate AP–MS and IF vector inputs (x_i and y_i for each protein i, see above) are compressed by modality-specific encoders (f_x and f_y) yielding 128-dimension vectors a and b:

where Dropout indicates dropout layers⁷¹; Linear indicates linear transformation layers; BatchNorm indicates batch normalization⁷²; Tanh indicates a hyperbolic tangent function; and ELU indicates an exponential linear unit function. The a and b vectors are then input to a joint encoder f_z that learns the L2-normalized 128-dimension latent representation z_i:

Values of z_i constitute the self-supervised multimodal embedding used for subsequent cell map evaluation (see the ‘Evaluation of embedding approaches’ section below) and construction (see the ‘Pan-resolution community detection’ section below). For the decoder step, z is reverse-transformed to extract 128-dimension modality-specific features through weight matrices w_x and w_y:

Finally, these features are passed to modality-specific decoders (g_x and g_y), yielding the 1,024-dimension reconstructed inputs (\(\hat\bfx\)_i, ŷ_i):

Loss functions

To compute the reconstruction loss R, the (\(\hat\bfx\)_i, ŷ_i) outputs of the autoencoder are compared to the original input values (x_i, y_i) for each modality:

where n is the total number of proteins. The overall reconstruction loss is the sum of modality-specific reconstruction losses and a regularization term, where λ_{regularization} is the regularization weight and ||w||_F is the F-norm of the matrix:

To compute triplet loss T, clustering using the Louvain algorithm⁷³ is performed on the (a, b) vectors of each modality (during early training clusters are defined using input (x, y) values instead; see the ‘Model training’ section below). This clustering defines selection functions S_x and S_y for each modality, with S(i,j) = 1 for proteins i, j in the same cluster, else 0. This information is used to compute T for each modality:

where N is the set of all proteins, D denotes the cosine distance (1 – cosine similarity), and m is the total number of terms inside the summation that are greater than 0. The full loss function L is a weighted sum of the reconstruction and triplet losses:

Model training

Model parameters were trained with standard neural network learning procedures provided by Pytorch⁷⁴ v.2.0.1, based on backpropagation using the Adam stochastic gradient descent method⁷⁵. Training occurred in three phases: (1) Over the first 200 epochs, only the reconstruction loss R was used for backpropagation. (2) Over an additional 200 epochs, the full loss function L was used for backpropagation, with S_x and S_y defined using input x,y vectors. (3) Over a final 500 epochs of training, the full loss function L was used for backpropagation, with S_x and S_y defined using a,b vectors (updated every 200 epochs). Values of hyperparameters were set based on previous work⁷⁰ without fine-tuning: batch size = 64, λ_{regularization} = 5, λ_triplet = 5, Adam optimization learning rate = 0.0001. Triplet loss margin and dropout percentages (ε = 0.10, dropout = 0.25) were set based on commonly recommended values^76,77.

Evaluation of embedding approaches

The above self-supervised embedding model was evaluated in comparison to two alternative multimodal embedding approaches: (1) simple unsupervised concatenation of the separate AP–MS and IF inputs (x,y); and (2) a random forest regression model supervised to use (x,y) to predict protein–protein semantic similarities from the Gene Ontology (June 2023 release), trained as previously described²¹ (Python Scikit-learn package, fivefold cross-validation, n_estimators=1000, max_depth=30). These embedding models were each scored for their recovery of interacting protein pairs documented in three complementary reference databases: (1) high-confidence protein–protein interactions in STRING^78,79 (v.12, NDEx uuid 0b04e9eb-8e60-11ee-8a13-005056ae23aa; Extended Data Fig. 2b,e); (2) protein pairs assigned to the same CORUM²⁵ complex (v.4.1, NDEx uuid 764f7471-9b79-11ed-9a1f-005056ae23aa; Extended Data Fig. 2c,e); or (3) protein pairs with high functional similarity in a genome-wide CRISPR-perturbation/mRNA sequencing screen (perturb-seq⁸⁰; Extended Data Fig. 2d,e). Here, high functional similarity was defined as the top 1% of protein pairs by Pearson correlation between the profiles of mRNA transcriptional changes induced by CRISPR disruptions of the two proteins (see the ‘Analysis of perturb-seq data’ section below).

Pan-resolution community detection

The cosine similaritiy between the multimodal embeddings for each pair of proteins was used to generate a series of protein–protein proximity networks in which edges were defined from the most similar 0.2, 0.3, 0.4, 0.5, 1.0, 2.0, 3.0, 4.0, 5.0 or 10.0% pairs, respectively, yielding 10 networks in total. Pan-resolution community detection was performed in each of these networks using the Hierarchical community Decoding Framework (HiDeF; https://github.com/fanzheng10/HiDeF)⁸¹, with a persistence threshold (k) of 10 and a maximum resolution (maxres) of 80, with other parameters kept at the default settings. HiDeF identifies protein communities at different resolutions and represents their hierarchical relationships as a directed acyclic graph (DAG). In this DAG, the nodes represent communities and the directed edges (a → b) represent that community a contains community b. The DAG was refined by assigning parent–child containment relationships between assemblies with containment index ≥ 75% and removing redundant systems with Jaccard index ≥ 90% with parent systems. This final DAG defines the cell map referenced in Fig. 2b.

Estimation of assembly diameter

A subset of 13 protein assemblies was selected from the cell map corresponding to assemblies with a known physical diameter documented in the literature (Supplementary Table 2). Linear regression was used to fit the log₁₀-transformed diameter (nm, y) against the log₁₀-transformed size of the assembly (number of proteins, x): y = 1.27x − 0.31. This linear equation was then used to estimate a diameter ŷ for each assembly in the map. A 95% prediction interval (PI) was estimated on the basis of the standard error as follows:

with t determined by the Student’s t-distribution (t = 2.2 with d.f. = n − 2, n = 13 components). The s.e. is the standard error between predicted and measured sizes, calculated as follows:

where, \(s_e=\sqrt\frac\sum _i=1^n(y_i-\haty)^2n-2\). Relevant to Fig. 2c.

Evaluation of assembly robustness

The robustness of protein assemblies was evaluated using a statistical jackknifing approach, as described previously²¹. A random set of 10% of proteins was removed before multimodal embedding (see the ‘Multimodal embedding overview’ section above); integration and community detection were then performed using the same parameters described in the ‘Model training’ and ‘Pan-resolution community detection’ sections. This randomization procedure was repeated 300 times to create a set of jackknifed hierarchies. The robustness of each assembly from the original hierarchy was then calculated as the fraction of all jackknifed hierarchies that contained at least one matching assembly, defined as substantial and significant overlap between the protein sets representing the target and the match (Jaccard index ≥ 40% and hypergeometric statistic FDR < 0.001). To assess the dependence of each assembly on the protein imaging data, we created a dataset with AP–MS features randomized (1,024-dimension random vectors sampled from a normal distribution) before the statistical jackknifing procedure, and the robustness of each assembly was computed as described above. For assessing the dependence of each assembly in the map on the AP–MS data, a reciprocal procedure was performed in which image embeddings were randomized. Relevant to Extended Data Fig. 3.

Annotation of cell map assemblies

The cell map was annotated by first aligning assemblies with the GO cellular component branch (June 2023 release), CORUM (4.1 human complexes) or HPA (v.23) resources. Each of these cell biology resources defines a list of protein sets (GO terms, CORUM complex, HPA subcellular localizations), referred to here as components. Hypergeometric tests were performed for each assembly versus each component in the resource, and the FDR was determined using BH correction. The results were tabulated for all assembly–component pairs with Jaccard index ≥ 10% and hypergeometric statistic FDR < 0.01 (Supplementary Table 1). Assemblies in the map were labelled as high overlap with known assembly (Jaccard index ≥ 50% for at least one of the three resources); substantial variation on known assembly (Jaccard index < 50% for all three resources and 20% ≤ Jaccard index < 50% for at least one of the resources); or not previously documented assembly (Jaccard index < 20% for all three resources) based on this enrichment analysis. We also used our recently developed Gene Set AI (GSAI) pipeline³ to guide the GPT-4 model²⁷ (v.gpt-4-1106-preview) to annotate assemblies with <1,000 proteins (Extended Data Fig. 4a). This approach uses a well-engineered prompt that follows the chain-of-thought⁸² and one-shot⁸³ strategies to query GPT-4 for a descriptive name, a confidence score and a detailed reasoning assay of the protein members from each assembly. One example is shown in Extended Data Fig. 4c, and the full result for each assembly is available in Supplementary Table 1. Literature references are provided by a separate GPT-4 based citation module developed in the previous study³ (Extended Data Fig. 4b) to aid in interpretability. The citation model extracts gene symbols and functional keywords from each paragraph of the LLM-generated analysis text; these are used to construct and execute PubMed queries that search titles and abstracts. The returned publications are prioritized based on relevance and the number of matching genes in their abstracts. Finally, a separate GPT-4 instance is asked to evaluate whether the top three publication titles and abstracts provide supporting evidence for factual statements in the original analysis paragraph, selecting those that satisfy this requirement as references. To evaluate the reproducibility of GPT-4 naming (Extended Data Fig. 4d), we performed the GSAI pipeline for five additional replicate runs of GPT-4 and calculated the semantic similarity between the assembly names generated in each of these runs versus the original run. Similarity was computed using the SapBERT model⁸⁴ from huggingface (cambridgeltl/SapBERT-from-PubMedBERT-fulltext) using the transformers package⁸⁵ (v.4.29.2). Assemblies that were not named by the original run were eliminated from the reproducibility test.

Biological condensate analysis

To analyse the cell map for biological condensates, we used three resources: IUPred3.0⁸⁶, a sequence-based predictor of protein disorder; FuzDrop⁸⁷, a sequence-based predictor for the ability of a protein to drive condensate formation; and CD-Code⁸⁸, a database containing proteins known to participate in biological condensates. IUPred3.0 predicts the probability of each amino acid in a sequence as being disordered. Proteins containing a contiguous sequence of amino acids >30 residues, where each amino acid has a >50% chance of being disordered, were annotated as likely disordered. FuzDrop assigns a probability of a sequence driving phase separation, which we thresholded at >60% to annotate a protein as ‘likely phase-separated’. Finally, we searched for each gene’s UniProtID in CD-Code (accessed 31 May 2023) under ‘Homo sapiens’, enabling us to annotate a protein as ‘associated with known condensates’. We used a hypergeometric test to assign statistical significance (P < 0.01) to each protein assembly that was enriched in proteins that were likely disordered, likely phase-separated, or associated with known condensates. Assemblies that were significant in one of these three analyses were considered possible biological condensates (Supplementary Table 3).

Validation of protein assemblies and subunits by SEC–MS data

For the set of proteins in each assembly, we determined the Pearson correlation in SEC–MS elution profiles for all pairs of these proteins (see the ‘SEC–MS data collection’ section). This similarity distribution was then compared to a null distribution (all pairs of proteins not in any common U2OS assembly, that is, assigned to root node only) using a one-sided Wilcoxon rank-sum test with BH correction (Fig. 3d and Supplementary Table 4). Assemblies with FDR < 5% were considered validated. A similar analysis was performed using PrinCE⁸⁹ (https://github.com/fosterlab/PrInCE) scores to rank protein pairs rather than Pearson correlations, with PrinCE run using the default parameters. We found that 90 assemblies were validated at 5% FDR in the complementary analysis using PrInCE, including 70 assemblies validated by both Pearson correlation and PrinCE similarity measures (Supplementary Table 4). For validation of unexpected protein subunits within assemblies, for each assembly <50 proteins, ‘unexpected proteins’ were defined as those not included in the best matching cellular component from any of three cell biology resources (GO, CORUM, HPA; see the ‘Annotation of cell map assemblies’ section above). For each unexpected member, its SEC–MS elution profile was compared against all other proteins in the assembly using Pearson correlation; this similarity distribution was compared to the null distribution as described above to compute an FDR. Unexpected proteins with FDR < 5% were considered validated (Supplementary Table 4).

AlphaFold-Multimer analysis

All pairs of proteins in small assemblies (<10 proteins) were selected for AlphaFold-Multimer analysis. AlphaFold-Multimer was run on each pair using localcolabfold (https://github.com/YoshitakaMo/localcolabfold) with the default settings⁹⁰. Sequences were acquired from the complete human protein UniProt FASTA file (UP000005640, reviewed sequences, downloaded 11 September 2023). For each predicted heterodimeric structure, we calculated a weighted average between the predicted template modelling score (PTM, an estimate of the similarity between the predicted and ground truth structures) and the ipTM score (the pTM score modified to score the interfaces across different proteins)³¹:

We calculated the median score out of five independent models generated per protein pair. A null score distribution was generated by repeating this score computation for pairs of proteins drawn randomly from those pairs that were not part of the same small assembly (<10 proteins as above). This null distribution was used to calculate an FDR for actual protein pair scores, selecting a cut-off of 30% corresponding to a weighted PTM score of 0.39. Pairs were further evaluated for the presence of a confident interface residue (within 10 Å of the other protein and plDDT score > 80). Relevant to Fig. 4a.

Integrative structure modelling of the Rag–Ragulator complex

A structural model of the Rag–Ragulator community was computed by using an integrative modelling approach^35,91,92,93, proceeding through the standard four stages^35,91,94 as follows. (1) Gathering input information: the Rag–Ragulator model in the cell map included LAMTOR1 through LAMTOR5, RRAGA, RRAGC, SLC38A9, BORCS6, NUDT3 and ITPA. An integrative model was computed based on the SLC38A9–RagA–RagC–Ragulator comparative model (PDB: 6WJ2 template)³⁶, AlphaFold³⁰ predictions for BORCS6 and ITPA, and pairwise AlphaFold-Multimer predictions³¹ for BORCS6 or ITPA versus all other members of the Rag–Ragulator complex. One-hundred AlphaFold-Multimer models were generated for each pair and evaluated using FoldDock⁹⁵. The model excluded NUDT3 because AlphaFold-Multimer did not produce high-confidence models of NUDT3 and other Rag–Ragulator components according to FoldDock. (2) Representing subunits and translating data into spatial restraints: the components of the Rag–Ragulator community were represented as rigid bodies. Alternative models were ranked through a scoring function corresponding to a sum of terms, each one of which restrains some aspect of the model based on a subset of input information. The spatial restraints included a binary binding mode restraint on the position and orientation of pairs of proteins as derived from ensembles of AlphaFold-Multimer predictions, connectivity restraints between consecutive pairs of beads in a subunit and excluded volume restraints between non-bonded pairs of beads. (3) Configurational sampling to produce an ensemble of structures that satisfies the restraints: the initial positions and orientations of rigid bodies and flexible beads were randomized. The generation of structural models was performed using replica exchange Gibbs sampling, based on the Metropolis Monte Carlo algorithm⁹⁶. Each Monte Carlo step consisted of a series of random translations of flexible beads and random translations and rotations of rigid bodies. (4) Analysing and validating the data and ensemble structures: model validation^93,97 included selection of the models for validation; estimation of sampling precision; estimation of model precision; and quantification of the degree to which a model satisfies the information used to compute it. The above four-step modelling protocol was scripted using the Python Modelling Interface (PMI) package, a library for modelling macromolecular complexes based on the open-source Integrative Modelling Platform (IMP) package v.2.18 (https://integrativemodeling.org)⁹¹. The configuration of the rigid Rag–Ragulator complex, ITPA protein and the two BORCS6 domains was computed by minimizing the violations of the spatial restraints implied by the input information, using IMP⁹¹. Relevant to Fig. 4j.

Analysis of perturb-seq data

The K562 day-8 perturb-seq dataset⁸⁰ was acquired at https://gwps.wi.mit.edu (BioProject: PRJNA831566). This dataset provides single-cell transcriptional profiles for 9,867 distinct gene knockouts, which underwent filtering based on the following criteria: (1) gene knockout corresponds to a protein in our U2OS cell map; (2) gene knockout has efficient on-target mRNA reduction of >30%; (3) gene knockout induces a strong transcriptional phenotype defined by ≥20 differentially expressed genes at a significance of P < 0.05 on the basis of the Anderson–Darling test followed by BH correction. This filtering process resulted in a list of 1,289 gene knockouts. The functional cell states due to each of these perturbations were represented using the mean-normalized differential expression profile. Relevant to Fig. 4m and Extended Data Fig. 2d,e.

Analysis of DPP9 inhibition

U2OS cells were seeded in triplicate at 300,000 cells per well in a six-well plate (two biological replicates). The next day, cells were treated with 1G244, a DPP9 inhibitor (HY-116304, MedChem Express) at the indicated concentrations for a total of 6 h. After treatment, The medium was aspirated and washed once with ice-cold PBS. Cells were collected in 500 µl of cold TRIzol reagent (15596026, Invitrogen) using a cell scraper. 100 µl of chloroform was added to the TRIzol lysate and vortexed for 20 s followed by a 3 min incubation at room temperature. The homogenate was centrifuged at 10,000g for 18 min at 4 °C. A total of 200 µl of aqueous phase was removed with a pipette and transferred to a new Eppendorf tube. An equal volume of 100% ethanol was slowly added to the aqueous phase and mixed by gentle pipetting. The entire sample was transferred to an RNeasy Mini spin column placed in a 2 ml collection tube (74104, Qiagen). The rest of the extraction was carried out according to the Qiagen RNeasy protocol. 2 µg of RNA per sample was reverse-transcribed according to the iScript cDNA Synthesis Kit protocol (1708890, Bio-Rad, interferon beta 1: Hs01077958_s1; interferon gamma 1, Hs00194264_m1; interferon gamma 2, Hs00988304_m1; non-ISG—18S, 4333760T; and GAPDH, Hs0275889q_g1). qPCR was carried out in triplicates in a 96-well plate according to the TaqMan Fast Advanced Master Mix protocol (4444557, Thermo Fisher Scientific) on a CFX96 Touch Real-Time PCR Detection System from Bio-Rad. The expression levels were compared against a housekeeping gene (GAPDH), and the relative expression levels were compared against the DMSO control. Relevant to Extended Data Fig. 6.

Analysis of conservation of U2OS assemblies in a second cell type

We downloaded the AP–MS BioPlex v3 network from NDEx (uuid 6b995fc9-2379-11ea-bb65-0ac135e8bacf), which provides high coverage of human protein interactions in a second cell type, HEK293 cells (14,033 proteins, 127,732 protein–protein interactions). Node2vec was used to represent the interaction pattern of each protein in this HEK293 network (see the ‘AP–MS and IF data preprocessing’ section). The cosine similarity in interaction patterns was then computed for all protein pairs (separately for HEK293 and U2OS). For the set of proteins included in each U2OS assembly, the distribution of pairwise protein similarities in HEK293 were compared to those in U2OS cells using the two-sided Mann–Whitney U-test. This test was translated to an effect size using Cliff’s delta⁹⁸; assemblies with Cliff’s delta ≥ 0.5 were considered to be increasingly U2OS-specific whereas those with Cliff’s delta < 0.5 were considered to be increasingly conserved. Relevant to Extended Data Fig. 7; in Extended Data Fig. 7b, Cliff’s delta scores of <0 are set to 0.

Multi-localization analysis

For each protein, we identified its terminal locations in the cell map hierarchy, defined as assemblies (hierarchy nodes) where the protein appeared but was absent in all subassemblies (child nodes). We then counted the number of unique paths from these terminal locations to the root of the hierarchy (root node). Proteins with multiple distinct paths to the root were classified as multi-localized, indicating their presence in different branches of the cell map. Multi-localized assemblies were identified as assemblies with more than one parent node in the hierarchy. Relevant to Extended Data Fig. 8.

Pre-processing of paediatric cancer mutational profiles

Data were obtained from a pan-paediatric cancer study⁴ of 914 individual patients with cancer aged under 25 years (study ID: pediatric_dkfz_2017, downloaded from cBioPortal^99,100). We selected the following types of non-silent somatic mutation events: ‘Frame_Shift_Del’, ‘Frame_Shift_Ins’, ‘In_Frame_Del’, ‘In_Frame_Ins’, ‘Missense_Mutation’, ‘Nonsense_Mutation’, ‘Nonstop_Mutation’, ‘RNA’, ‘Splice_Region’, ‘Splice_Site’ and ‘Translation_Start_Site’. A total of 772 primary tumour samples, spanning 18 cancer types, were in the resulting list (Supplementary Table 9). We recorded the number of tumours in the pan-paediatric cohort, as well as each individual tumour cohort, in which each gene was observed to have at least one somatic mutation event (N_(g,obs)). Moreover, we calculated the expected number of mutations for each gene in the pan-paediatric cohort (N_(g,exp)) using the default setting of MutSigCV v.1.4, as described in a previous study¹⁰¹. For expected mutation counts for individual cancer cohorts, we down-scaled the pan-paediatric cancer N_(g,exp) based on the proportion of patients (for example, 44 patients with Wilms’ tumours (WT) account for 5.7% of the pan-paediatric cohort, so N_g,exp,WT = 0.057 × N_{g,exp,pan-paediatric}). Finally, the corrected log mutation count of each gene (M_g) for each cohort was calculated as:

Statistical identification of recurrently mutated assemblies

We applied a previously described statistical model, HiSig¹⁰¹ (https://github.com/fanzheng10/HiSig), to calculate the mutation selection pressure on assemblies with the default parameter settings. HiSig implements linear regression (with L1 lasso regularization) of the mutation count against the organization of proteins in assemblies. We calculated an empirical P value by comparing the mutational selection on assemblies against 10,000 randomly permuted assignments of proteins to assemblies. The FDR was calculated by BH correction. Recurrently mutated assemblies were selected on the basis of FDR ≤ 0.4. Assembly-level mutation frequencies were calculated from the number of distinct patients who carried at least one mutated protein in the assembly. Tumour types with fewer than 15 patients were excluded from analysis, as were mutated assemblies with >50 mutated proteins.

Validation of cancer driver genes

Genes mutated in more than one patient with cancer and located in the significantly recurrent mutated assemblies (see above) were defined as putative cancer proteins. We obtained a large collection of transposon-based mutagenesis screens in mice from the Candidate Cancer Gene Database (CCGD)⁴⁶ (http://ccgd-starrlab.oit.umn.edu/index.html, downloaded on 26 March 2024). This database consists of a total of 72 studies with mouse transposon insertion mutagenesis screens across 13 tumour categories (Extended Data Fig. 9a). We determined the number of studies in which a gene was disrupted by transposon insertion in mice tumours. Mutated genes in cancer assemblies were designated positives (genes expected to have high study counts because they are mutated), and all other genes were designated negatives (genes not expected to have high study counts). We calculated the kernel density estimation (KDE) for the mutated genes in cancer assemblies and other genes in the cell map using the stat.gaussian_kde function from the Python package scipy (v1.7.3). The area under the KDE curves was integrated using the trapz function from Python package numpy (v.1.21.6). The FDR was then computed as the ratio of the area under the curve for false positives (Area_FP) to the total area under the KDE curve representing both false positives and true positives (Area_TP), mathematically shown as: \(\rmFDR=\frac\rmArea_\rmFP\rmArea_\rmFP+\rmArea_\rmTP\). We specified the minimum number of screens reporting a gene at 4 (x ≥ 4), corresponding to FDR = 0.28, as the threshold cut-off for validated cancer drivers (Extended Data Fig. 9b). Adult cancer driver genes were collected from the TCGA Pan-Cancer Atlas¹⁰²; significantly mutated genes in the pan-paediatric cancer cohort were collected from refs. ^4,103. These genes were defined as known cancer genes in Extended Data Fig. 9c,d.

Running the cell mapping toolkit

The Cell Mapping Toolkit (https://github.com/idekerlab/cellmaps_pipeline) implements a series of Python packages to execute the end-to-end pipeline described herein. Specific packages include steps for processing the protein imaging and biophysical interaction datasets (cellmaps_imagedownloader, cellmaps_ppidownloader), embedding the input modalities (cellmaps_image_embedding, cellmaps_ppi_embedding), integrating the modalities (cellmaps_coembedding), constructing the hierarchical cell map (cellmaps_generate_hierarchy) and annotating the cell map with known resources such as GO (cellmaps_hierarchyeval). Each package is pip-installable and is linked to complete user documentation hosted at ReadTheDocs (https://cellmaps-pipeline.readthedocs.io/). A step-by-step guide is provided at the GitHub repository.

Statistics and reproducibility

Statistical tests were performed using SciPy¹⁰⁴ with BH multiple-testing correction where appropriate. Statistics involving comparison between two data distributions were calculated using Mann–Whitney U-tests or Wilcoxon rank-sum tests (Figs. 2d, 3c,d and Extended Data Figs. 2b–d, 7b, 9b). Statistics for assessing the enrichment of proteins or protein pairs were calculated using hypergeometric tests (Fig. 2b and Extended Data Fig. 3) unless stated otherwise. The SEC–MS data were reproduced in three biological replicates. The IF stainings were reproduced in at least two different cell lines in HPA (Fig. 4h,l and Extended Data Figs. 6b, 7d, 8c,g, 9f). The qPCR experiment for DPP9 was repeated for two biological replicates and three technical replicates each (Extended Data Fig. 6c).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.