China RSL database
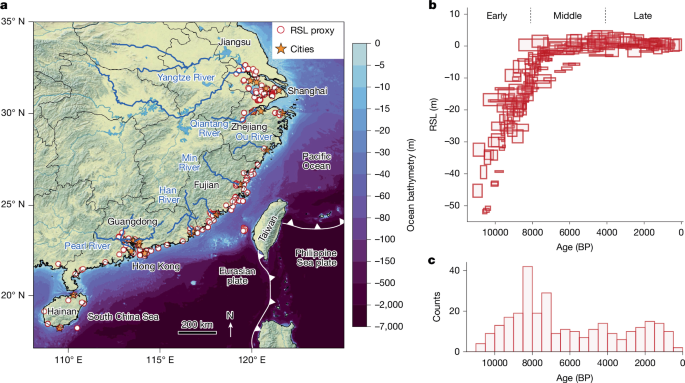
We compiled an up-to-date southeastern China RSL database, containing sea-level index points (SLIPs, data that define the discrete position of past sea level in space and time) from published literature comprising various types of geological proxy, such as diatoms, beachrock and mangroves22,30,34,51,52,53,54,55,56. The database was then standardized following the methodology in ref. 57. Each database entry consists of reconstructed RSL, RSL reconstruction uncertainty, sample age, age measurement uncertainty and a binary index indicating basal or intercalated sediment sequence (that is, whether subject to potential sediment compaction uncertainty). We did not apply any corrections to RSL change caused by tectonic or sediment compaction because we treated them as our target signals to infer from the hierarchical model. All SLIPs used in this study were radiocarbon dated: we recalibrated the conventional radiocarbon age using the IntCal20 calibration curve58 for terrestrial samples and Marine20 (ref. 59) for all marine samples. For marine samples, we apply appropriate, updated (that is, calculated using Marine20) local marine reservoir corrections (ΔR; http://calib.org/marine).
Spatiotemporal statistical analysis
To estimate past trend and rates of RSL change and associated uncertainties, we used PaleoSTeHM60 to construct a spatiotemporal hierarchical model61 that consists of three hierarchical levels: (1) the data level, which describes how spatiotemporal RSL data were recorded with several uncertainty sources; (2) the process level, which models the latent process of spatiotemporal RSL change; (3) a parameter level that defines prior distributions for hyperparameters used in levels (1) and (2). For computational efficiency, we used an empirical Bayesian analysis approach; in other words, the hyperparameters used to define prior distributions are point values optimized from maximum likelihood estimation62.
Following the notation in ref. 13, at the data level, reconstructed RSL (yi) is modelled as:
$$y_i=f(x_i,t_i)+\epsilon _i^y+y_(x_i)+\omega (x_i,t_i)+y_i\gamma $$
(1)
$$t_i=\widehatt_i+\epsilon _i^t$$
(2)
$$y_(x)\approx \mathcalGP\0,\sigma _^2\delta (x,x^\prime )\$$
(3)
$$\omega (x,t)\approx \mathcalGP\0,\sigma _\omega ^2\delta (x,x^\prime )\delta (t,t^\prime )\$$
(4)
$$\gamma \approx \mathcalGP\0,y\beta \sigma _\gamma ^2\delta (x,x^\prime )\delta (t,t^\prime )\$$
(5)
in which xi is the noise-free spatial location of the ith observation, ti is its true age, \(\widehatt_i\) is the mean observational age and \(\epsilon _i^t\) and \(\epsilon _i^y\) are uncertainties in the age measurement and RSL reconstruction, respectively, which we assume to be independently and normally distributed. The notation \(\mathcalGP(\mu ,k(x,x^\prime ))\) indicates a GP prior with mean μ and covariance function k(x, x′). y0(x) is a site-specific datum offset to ensure that the RSL reconstructions are directly comparable with each other, δ is the Kronecker delta function, ω(x, t) is supplemental white noise and γ is set to allow uncertainty related to sediment compaction, in which β is a binary vector specifying that either each record is basal (β = 0) or intercalated sediment (β = 1) sequence. γ is multiplied by y, so a deeper sample is prone to have larger compaction uncertainty, which is a simplified formulation and may not fully capture autocompaction processes63,64.
We use a noisy-input GP method65 to translate geochronological uncertainties into corresponding vertical uncertainty using first-order Taylor series approximation:
$$f(x_i,t_i)\approx f(x_i,\widehatt_i)+\epsilon _i^t\frac\partial f(x_i,\widehatt_i)\partial t$$
(6)
At the process level, we model the latent RSL field f(x, t) as a GP:
$$f(x,t)\approx \mathcalGP(h_\rmGIA(x,t| \Theta ),\Sigma (x,t))$$
(7)
in which hGIA serves as the mean function for the GP (that is, explicit basis function in ref. 62) described by linear combinations of a GIA model ensemble, which predicts RSL change at any location and time based on given physical parameters Θ = [θ1, θ2,…, θJ] (J = 360). More details about GIA model parameters are given in the GIA section below. We assume that hGIA follows a multivariate normal distribution:
$$h_\rmGIA(x,t| \Theta ) \sim \mathcalN(\mu _\rmGIA(x,t| \Theta ),\Sigma _\rmGIA(x,t| \Theta ))$$
(8)
in which μGIA(x, t|Θ) is a weighted mean function of the GIA model ensemble:
$$\mu _\rmGIA(x,t)=\mathop\sum \limits_j=1^J\alpha _j\rmGIA(x,t| \theta _j)$$
(9)
GIA(x, t|θj) stands for GIA model prediction at location x and time t, given a specific set of physical model parameters θj. αj is the weighting factor for the corresponding GIA model, which is calculated by:
$$\alpha _j=\frac\exp (-0.5\chi _j^2)a$$
(10)
$$\chi _j=\frac1n\sqrt{\mathop\sum \limits_i=1^n\left[\frac \theta _j))^2(\epsilon _i^y)^2+\frac(\widehatt_i-t^* )^2(\epsilon _i^t)^2\right]}$$
(11)
in which χj represents a unitless metric to measure data-model misfit by calculating the minimum distance between each RSL data and GIA model and t* indicates the age when GIA model prediction shows the minimum distance relative to the observation66. a is a normalizing constant to ensure that the sum of all α values is 1 and n is the number of RSL data in our database. Similarly, ΣGIA(x, t|Θ) is the sample covariance matrix of the GIA model ensemble, weighted by α. The prior and posterior of the GP mean function can be found in Extended Data Table 2.
Making use of a GIA model ensemble conditioned on observational data, we decompose GIA-related contributions into GMSL change (GIAg(t); that is, barystatic signal) and associated GRD effects (GIAGRD(x, t)):
$$\rmGIA(x,t)=\rmGIA_\rmg(t)+\rmGIA_\rmGRD(x,t)$$
(12)
Here GIAg(t) is calculated following the methodology in ref. 67, incorporating the spatiotemporally variable RSL impact on calculation of ice volume above flotation and temporally evolving global ocean surface area. The GIAGRD(x, t) component is then derived as the difference between the local GIA model prediction and GIAg(t).
Because a mean function was set for GP prior, the GP covariance function Σ(x, t) (see equation (7)) is essentially modelling the residual between observation and mean function (that is, processes that cannot be captured by the GIA model). Putting them together, the process-level model can be written as:
$$\beginarraycf(x,t)=\rmGIA_\rmg(t)+g(t)+\rmGIA_\rmGRD(x,t)+m(x)(t-t_)+r(x,t)\\ \,+l(x,t)\endarray$$
(13)
in which t0 is a reference time point (defined as 0 BP or 1950 CE, the reference year for radiocarbon dating). There are four more components with GP priors incorporated: (1) g(t), a common term across all sites, primarily reflecting contributions from processes that are not explained by GIAg(t), for example, centennial GMSL fluctuations (as GIAg(t) typically has a temporal resolution of 500–1,000 years), GMSL variation associated with mountain glaciers and global thermosteric expansion; (2) m(x)(t − t0), a spatially varying (can be either local or regional, depending on data preference), temporally linear field, which indicates slow-changing processes over the Holocene, such as tectonics, long-term sediment compaction and sediment isostatic adjustment18,63; (3) r(x, t), a regional-varying and temporally nonlinear term that reflects atmosphere/ocean dynamics-induced sea-level change and regional tidal range variation8; (4) l(x, t), a locally varying, temporally nonlinear signal that indicates highly localized processes such as small-scale sediment compaction, local hydroclimate variation and seismic events.
To further account for short-term and long-term nonlinear sea-level variability, we separate covariance functions (that is, kernels) (1), (3) and (4) into a fast (<300 years temporal length scale) and a slow (>300 years temporal length scale) component, so that equation (13) becomes:
$$f(x,t)=g_\rmf(t)+g_\rms(t)+\rmGIA_\rmg(t)+\rmGIA_\rmGRD(x,t)+m(x)(t-t_)+r_\rmf(x,t)+r_\rms(x,t)+l_\rmf(x,t)+l_\rms(x,t)$$
(14)
Therefore, the final process function contains nine components, represented by seven covariance functions, including fast and slow spatially uniform terms gf(t) and gs(t); a temporally linear term m(x)(t − t0); fast and slow temporally nonlinear and spatially varying terms rf(x, t) and rs(x, t); fast and slow temporally nonlinear and locally varying terms lf(x, t) and ls(x, t); and two GIA components mentioned above. Because g(t) and GIAg(t) both reflect a globally uniform signal, we interpret them together as the final GMSL change signal. Hyperparameter optimization results can be found in Extended Data Table 3.
To ensure that our GMSL estimate captures the global signal rather than an average for China, we first tested GIA model predictions (GIAg(t) + GIAGRD(x, t)) against RSL data from various locations outside China, independent of our GIA ensemble calibration. The results indicate that a China-constrained GIA model prediction generally aligns well with RSL data from Australia, Singapore, the Mekong River Delta and South Sulawesi57,68,69,70 (Extended Data Fig. 6), suggesting that it serves as a good approximation of latent GMSL variation. To incorporate centennial-scale GMSL variability into our hierarchical model, we include a high-resolution GMSL reconstruction during the past three millennia. This reconstruction was developed on the basis of high-resolution SLIPs, many with sub-decadal and sub-decimetre uncertainty, with a broader set of tide gauges. This global GMSL reconstruction was generated independently of China sea-level analyses mentioned above, following the methodology in ref. 14, which integrates high-resolution instrumental observations with geological proxies in a consistent framework. We made some modifications, including further data from regions such as the Falkland Islands71,72, New Zealand73, Australia74, Pohnpei and Kosrae75, Israel76, Croatia77, Ireland78 and Florida79 (see Extended Data Fig. 1), and recalibrated the hyperparameters of the model accordingly (Extended Data Table 3). Furthermore, for post-twentieth-century GMSL estimates, we used the recent reconstruction in ref. 9 instead of that in ref. 80.
This hybrid model greatly enhances performance compared with earlier approaches that rely only on GIA models to describe observed Holocene sea-level changes26. Model validation through a tenfold cross-validation test demonstrates that incorporating the GP model reduces the mean squared prediction error from 13.9 m2 to 5.18 m2 and increases the percentage of observations falling within ±2σ of the model predictions from 72.83% to 97.83% (Extended Data Fig. 7). Furthermore, the inclusion of the GIA model ensemble not only captures the non-Gaussian dynamics of sea-level change but also provides more physically interpretable decomposition results, especially for the early Holocene (see also the purely statistical model60). Building on this physically informed foundation, the GP components can therefore capture further, physically meaningful variability—such as centennial-scale GMSL fluctuations and regional climate variability—that become increasingly influential in the late Holocene and modern periods.
Mathematical formulation of the spatiotemporal covariance function
Each covariance function (that is, kernel) in equation (14) is constructed using the following common GP kernels:
$$K_\rmM^1/2(a;\sigma ,\tau )=\sigma ^2\exp \left(-\frac a-a^\prime \tau \right)$$
(15)
$$K_\rmM^3/2(a;\sigma ,\tau )=\sigma ^2\left(1+\sqrt3\times \frac a-a^\prime \tau \right)\exp \left(-\frac \tau \right)$$
(16)
$$K_\rmLinear(a;\sigma )=\sigma ^2(a\cdot a^\prime )$$
(17)
in which |a − a′| can either indicate distance in time (t) or angular distance in space (x). \(K_\rmM^1/2\) and \(K_\rmM^3/2\) represent Matérn kernels with smoothness parameters 1/2 and 3/2; the former is non-differentiable and the latter is once differentiable. σ and τ are two kernel hyperparameters defining the amplitude and temporal/spatial length scales of that kernel. On the basis of these expressions, seven terms in our GP kernel can be written as:
$$g_\rmf(t)=K_\rmM^3/2(t;\sigma _\rmg_\rmf,\tau _\rmg_\rmf^t)$$
(18)
$$g_\rms(t)=K_\rmM^3/2(t;\sigma _g_\rms,\tau _g_\rms^t)$$
(19)
$$m(x)(t-t_)=K_\rmM^1/2(x;1,\tau _m^x)\cdot K_\rmLinear(t;\sigma _m)$$
(20)
$$r_\rmf(x,t)=K_\rmM^1/2(x;\sigma _r_\rmf,\tau _r^x)\cdot K_\rmM^3/2(t;1,\tau _r_\rmf^t)$$
(21)
$$r_\rms(x,t)=K_\rmM^1/2(x;\sigma _r_\rms,\tau _r^x)\cdot K_\rmM^3/2(t;1,\tau _r_\rms^t)$$
(22)
$$l_\rmf(x,t)=K_\rmM^1/2(x;\sigma _l_\rmf,\tau _l^x)\cdot K_\rmM^3/2(t;1,\tau _l_\rmf^t)$$
(23)
$$l_\rms(x,t)=K_\rmM^1/2(x;\sigma _l_\rms,\tau _l^x)\cdot K_\rmM^3/2(t;1,\tau _l_\rms^t)$$
(24)
GIA modelling
RSL change signals associated with ice–water mass exchange-induced GMSL variations and GRD effects were computed using a GIA model grounded in gravitationally self-consistent theory that accounts for migrating shorelines and Earth rotational feedback17,81,82. Over the timescales of interest, the deformational effects exhibit viscoelastic behaviour, allowing RSL change to be separated into components representing the instantaneous response of the solid Earth and sea surface to meltwater influx and the continuing adjustments owing to past surface load changes.
The GIA model requires two critical physical inputs: solid Earth rheology and global ice history. In this study, the Earth is represented as a spherically symmetric, radially stratified (that is, 1D), self-gravitating Maxwell body comprising an elastic lithosphere and a mantle stratified into an upper mantle (extending to 670 km) and a lower mantle (extending from 670 km to the core–mantle boundary). The elastic and density structure is based on the preliminary reference Earth model83. Present-day topography is based on ETOPO2 (ref. 84). To account for uncertainties in Earth rheology, we tested lithospheric thicknesses of 71 and 96 km, upper mantle viscosities ranging from 0.05 to 0.80 × 1021 Pa s and lower mantle viscosities of 1 to 3 × 1021 Pa s, constrained by a previous GIA study on sea-level changes in China26.
In total, 15 ice models were tested in this study, including two commonly used models, ANU20 and ICE-6G_C (ref. 19), supplemented by 13 more ice models from ref. 85 to bridge the sampling gap between ANU and ICE-6G_C. These extra models were generated by sampling the variability between various published ice sheet reconstructions85. In total, 360 ice–Earth model combinations have been computed with spherical harmonic truncation of degree and order 256 (that is, 70–80-km spatial resolution). We do not consider Earth models with laterally varying Earth rheology in this study because: (1) seismic tomography indicates minimal lateral variation in lithospheric thickness and upper mantle viscosity in southeastern China86, with RSL insensitive to slight lower mantle variations owing to China’s far-field location20; (2) calibrating our GIA model ensemble to southern (15–25° N) and northern (25–35° N) data subsets favours similar Earth parameters (Extended Data Fig. 8); (3) 1D GIA models enable comprehensive sampling of ice and Earth parameter uncertainties, the primary uncertainty source for Holocene China sea-level change, whereas the computational burden of 3D models limit such sampling. These model calibration results can be found in Extended Data Fig. 8.
Although this GIA model captures shoreline migration from ice–ocean mass exchange, it omits sediment-driven landscape evolution, which substantially reshapes the land–ocean boundary in megadelta systems such as the YRD during the Holocene. For instance, during early Holocene postglacial transgression, the elevation of Taizhou (Fig. 2c) was much lower than today, requiring tens of metres of middle to late Holocene sediment deposition to reach land elevation29. Thus, Taizhou should be classified as ocean until sediment accumulation elevated it. As the GRD signal typically involves coastal and continental uplift and offshore subsidence, land–ocean misclassification in GIA models using modern topography overestimates GRD calculations (whereas GMSL remains unchanged), requiring compensatory overestimation of the linear subsidence term to fit the observations.
Although developing and validating a time-evolving topography in the GIA model is beyond the scope of this study, we conducted a test to quantify an upper bound of this GRD overestimate. Using a Holocene sediment age–depth database87, we reconstructed palaeo YRD topography at 8500 BP (when most YRD sea-level data formed) using a similar GP formulation as our sea-level model (but with zero mean function without the fast-changing terms). Rerunning the GIA model with palaeotopography and comparing it with the original model using modern topography quantifies how the assumption of modern topography overestimates GRD, with the true process lying between these two scenarios. For this experiment, we used an Earth model with a 96-km lithosphere, 0.01 × 1021 Pa s upper mantle and 1 × 1021 Pa s lower mantle viscosity (best-fitting Earth model for China sea-level data) paired with a best-fitting ice model (model 1219 in ref. 85).
The palaeotopography experiment results show that the land–ocean mask was located further inland during the early Holocene when middle to late Holocene sediment deposits are removed (Extended Data Fig. 3c). This landward mask shift suggests an overall GRD overestimate in the original GIA model assuming modern topography during the early Holocene, particularly near the Yangtze River mouth (Extended Data Fig. 3f). Following the large marine transgression during the middle and late Holocene, this GRD overestimate rapidly decreased to near zero between 6000 and 5000 BP as regional GRD in the YRD is governed by broader-scale uplift signals related to continental shelf inundation, which produce nearly identical signals in both experiments. We quantified this GRD overestimate for each sea-level data point based on location and age to assess its potential impact on our linear term. Removing this potential GRD overestimate from the linear term reconstruction indicates that, although the land–ocean mask change leads to slight overestimation of subsidence rates, the overall subsidence pattern in the YRD remains robust (Extended Data Fig. 3l).
Palaeo tidal variation impact on sea-level reconstruction
Palaeo sea-level reconstructions rely on a quantifiable relationship between a specific sea-level indicator and the contemporaneous reference water level and indicative range88. This relationship is commonly constructed on the basis of modern field-based survey relative to modern tidal datum, assuming that there is no change in tidal range through time88. However, several tidal modelling analyses have suggested that tidal regimes are subjected to great variation through time owing to sea-level change and landscape evolution53,89,90. As a result, assuming temporally uniform reference water level and tidal range can result in systematic bias in sea-level reconstructions and their associated uncertainties.
Systematically quantifying temporally varying tidal regime impact on sea-level reconstruction requires an accurate estimate on sea-level change and landscape evolution, owing to sediment transport in the past. This requires extensive field surveys and modelling efforts and is at present beyond the scope of this study. However, here we use a global postglacial tidal modelling study89 to demonstrate the potential impact of tidal variation. This study uses a truly global barotropic ocean tide model that considers the non-local effect of self-attraction and loading and can produce model tide with 65–70% of agreement compared with tide gauge measurements. Although this model only uses one postglacial sea-level change history, produced by the ICE-6G_C ice model with the VM5a Earth model and no consideration of landscape evolution, its results can still provide some meaningful information on the potential magnitude of sea-level reconstruction errors owing to tidal variation.
On the basis of this model, we calculate the biases in sea-level reconstruction and its uncertainty for each data point, based on its reference water level and indicative range. For example, the reference water level indicative range of lower tidal flat sediment with dominantly brackish water benthic diatoms with some planktonic types is quantified as the middle between mean tide level (MTL) and mean lower low water (MLLW) and within the range of MTL and MLLW. On the basis of model output from ref. 89, the present-day reference level and reference level and indicative range for a lower tidal flat sediment from Hong Kong can be expressed as:
$$\rmReference\,\rmlevel=[0+(-0.8)]/2=-0.4\,(\rmm)$$
(25)
$$\rmIndicative\,\rmrange\,\rmuncertainty=0\,\rmto-\,0.8\,(\rmm)$$
(26)
in which 0 and −0.8 m are the model-produced present-day MTL and MLLW. Assuming that the indicative range stands for 4σ reconstruction uncertainty, the uncertainty here is 0.2 m. If the sample was dated to 9000 BP, we calculate the palaeo indicative range using the same model, which may give:
$$\rmPalaeo\,\rmreference\,\rmlevel=[-0.1+(-1.2)]/2=-0.65\,(\rmm)$$
(27)
$$\rmPalaeo\,\rmindicative\,\rmrange=-0.1\,\rmto-\,1.3\,(\rmm)$$
(28)
in which −0.1 and −1.2 m are the model-produced MTL and MLLW at 9000 BP. Here the reconstructed uncertainty should be 0.3 m. The biases for sea-level reconstruction and its uncertainty can then be calculated as:
$$\rmReference\,\rmlevel\,\rmbias=-0.65-(-0.40)=-0.25\,(\rmm)$$
(29)
$$\rmIndicative\,\rmrange\,\rmuncertainty\,\rmbias=0.3-0.2=0.1\,(\rmm)$$
(30)
Overlooking tidal variations can introduce an absolute bias of 0.25 m in sea-level reconstructions, along with an extra 0.1 m of unaccounted uncertainty. Using the tidal model from ref. 89, we calculate all sea-level reconstruction biases and uncertainties. Because this tidal model is based on the ICE-6G_C ice history, we also assessed the impact of ice history uncertainty by performing similar calculations with tidal model time series that were either delayed or advanced by 1,000 years. The results, shown in Extended Data Fig. 9a,b, indicate that the potential influence of tidal range variation on sea-level proxy interpretation decreases substantially after about 6,000–5,000 BP, when regional sea level stabilized.
Analytical model for river discharge impact on sea level
To calculate river discharge anomaly impact on local sterodynamic sea-level change, we applied an analytical model from ref. 91. Specifically, we applied the theory developed for Buenos Aires, in which local river channels are relatively shallow, narrow and fresh, similar to Qiantang River mouth near Hangzhou. Following the notation in ref. 91, the sterodynamic sea-level change can be written as:
$$\langle \zeta \rangle =\fracC_\rmdUqg\int _x^\infty \frac1H^2W\rmdx^\prime $$
(31)
in which ζ represents sterodynamic sea level, Cd is the drag coefficient, U is a reference velocity scale, q is river streamflow and g is the acceleration owing to gravity. H and W are the river depth and width profiles, respectively. We use the default value for CdU from the original study (0.001 m s−1), whereas H and W for the Qiantang River were sourced from ref. 92.
On the basis of local river discharge data from 1995–2020 provided in ref. 93, the average discharge for wet, normal and dry years at the Qiantang River is 1,450, 1,004 and 752 m3 s−1, respectively. Using these values, the resulting sterodynamic sea-level changes related to river discharge at various distances from the river mouth are shown in Extended Data Fig. 9c.
Modern instrumental-based sea-level budgets
To compare our reconstruction with instrument-data-based modern estimates, we used a recent analysis9 that describes post-1900 sea-level budgets. This analysis integrates Kalman smoother-calibrated process-based models with reduced spatial optimal interpolation of satellite altimetry to reconstruct global sea-level budgets, a method that has been used to explain sea-level budget in several regions94,95. For the northwestern Pacific Basin, this reconstruction achieved a 0.94 correlation coefficient with satellite altimetry data since 1993 to 2021, suggesting robust reconstruction performance.
The sea-level budget reconstruction accounts for GMSL, modern GRD (effects from recent mass exchange between the ocean, glaciers, ice sheets and water impoundment in artificial reservoirs), as well as ocean dynamic contributing to RSL change, accounting for inverse barometer effects. The ocean dynamic signal is derived by subtracting the global mean thermosteric expansion from the sterodynamic signal. For each city, we calculate each sea-level budgets component using a regional average value (that is, weighted averaging the three closest oceanic grid cells relative to the city centre). To better align the annual resolution sea-level budgets in ref. 9 with our geological reconstruction, we apply a 20-year moving average filter for all signals.
Modern VLM observations
We use modern VLM rate measurements from the GNSS and InSAR. The GNSS-derived VLM rates were sourced from the Nevada Geodetic Laboratory at the University of Nevada (https://geodesy.unr.edu (ref. 48)), aligned to the IGS14 reference frame96. The VLM trends and uncertainties provided by the Nevada Geodetic Laboratory are based on the Median Interannual Difference Adjusted for Skewness (MIDAS), a robust trend estimator for accurate GNSS velocity97, which helps minimize the influence of seasonal variations and other temporal anomalies (for example, hydrological cycles and seismic events) that might affect trend estimation. In total, 82.6% of collected GNSS sites have a duration of at least 10 years and 69.6% have a duration of at least 15 years.
The InSAR-derived VLM rates from 2015 to 2022 CE were obtained from a national-scale assessment of land subsidence in China’s main cities44. This study used GNSS-calibrated Sentinel-1 data to systematically quantify land subsidence across 82 main Chinese cities. For each city, their VLM trends are presented as the median, along with the 5th and 95th percentiles, reflecting the spatial variability in VLM within each urban area. To generate geological VLM estimates from our model, we first select all coastal cities conditioning on the geological observations, which reduces the variance by at least 5% to the prior in our model. We then generated a spatial VLM map for each city within a 50-km radius and computed the same quantities as in ref. 44, incorporating spatiotemporal hierarchical modelling uncertainty.