Pre-rupture pipeline inventories
We estimate the mass of CH4 contained in each pipeline before rupturing using equation (1):
$$M_\rmNSx=L_\rmNSx\times \rho _\rmNSx\times 0.25\,\times D_\rmNSx^2\times \rm\pi \times C_\rmNSx/\mathrm1,000$$
(1)
where MNSx is the mass of CH4 contained within pipeline NSx (kt of CH4), LNSx is the total pipeline length in kilometres (km), ρNSx is the density of the natural gas mixture at the pressure and temperature within the pipeline (kg m−3), DNSx is the pipeline diameter (m), and CNSx is the percentage mass composition of CH4 in the natural gas (Extended Data Tables 1 and 2). In equation (1), we use ρNSx values from the gas mixture eventually used in the PBREAK simulations because our CATHARE simulations do not consider components in the mixture that make up less than 0.1% (Extended Data Table 2).
Pipeline emission simulation tools
We use PBREAK36 (version 2.28.3) and CATHARE (version CATHARE-337) to simulate pipeline rupture emission from NS1A, NS1B and NS2A. PBREAK is a mathematical model used to simulate the outflow of gas following the sudden puncture or rupture of a high-pressure transmission pipeline36,47,48,49. The model is embedded in the PIPESAFE Quantitative Risk Assessment software. CATHARE is a tool developed by the French Alternative Energies and Atomic Energy Commission used for thermal hydraulic simulations of multiphase flows (https://cathare.cea.fr)37,50,51,52,53. Both model pipeline depressurization as the one-dimensional flow of natural gas in a pipeline and solve a system of three conservation equations for mass, momentum and energy. The models use an equation of state to compute fluid properties (Supplementary Discussion 3). Further descriptions of each model, including their suitability for modelling subsea pipeline ruptures, are provided in Supplementary Method 1.
PBREAK
Within the PBREAK workflow, each pipeline is divided in N segments, and the nonlinear equations for continuity and mass balance, momentum and energy solved at each time step using an implicit finite-difference scheme36. These equations are solved every 1 s for the first 2 min, then every 30 s until the calculation finishes. The computation terminates when the internal pressure in all the lengths of each pipeline is equal to the external pressure. The model results are the variation with time of the outflow at the point of rupture coming from each branch of pipeline, and the cumulative flow from the beginning of the release.
CATHARE
We discretize each of the three pipelines into one-dimensional elements meshed with a series of cylinders. We define the cross-section (A), friction perimeter (χf) and roughness of the pipelines. In the case of monophasic calculations, CATHARE solves a system with three main variables (pressure P, enthalpy H and velocity V) and three conservation equations (equations (2)–(4): conservation of mass, momentum and energy):
$$A\times \frac\partial \rho \,\partial t+\frac\partial (A\times \rho \times V)\partial z=0$$
(2)
$$A\times \rho \times \left(\frac\partial V\,\partial t+V\times \,\frac\partial V\,\partial z\right)+A\times \frac\partial P\,\partial z=-\,\chi _\rmf\times C_\rmf\times \rho \times \frac V2+A\times \rho \times \,g_z$$
(3)
$$A\times \frac\partial \partial t\left[\rho \times \,\left(H+\,\fracV^22\right)\right]+\frac\partial \,\partial z\left[A\times \rho \times V\times \left(H+\,\fracV^22\right)\right]-A\times \frac\partial P\,\partial t=\chi _\rmc\times q_\rmw+A\times \rho \times V\times g_z$$
(4)
We add thermal structure to each of the cylinders by specifying their heating perimeter (χc). The heat conduction through the wall structures is resolved by a multilayer radial discretization and we define the heat exchange with an external fluid. The pipelines are assumed to be horizontal (gravity projection gz equal to 0 in equations (3) and (4)).
The one-dimensional elements use a first-order finite-volume scheme with a staggered mesh and the donor-cell principle. The time discretization is fully implicit. The mass and energy equations in CATHARE use a conservative form and are discretized to ensure mass and energy conservation. The wall conduction is implicitly coupled with the hydraulic calculations. The nonlinear system of equations is solved in several steps using an iterative Newton–Raphson method. The numerical resolution allows the model to consider sonic flow as a boundary condition during the pipeline rupturing.
The fluid equation of state is computed by coupling CATHARE with the REFPROP library from the National Institute of Standards and Technology54, which uses the GERG-2008 equation of state55 to compute properties (such as density ρ) for natural gas mixtures. We use two closure laws to model the interaction between the internal fluid and the pipe wall. Given the high gas velocity and the large pipe diameter, the flow is deemed fully turbulent throughout the transient (Reynold’s number exceeding 3,000). Therefore, the wall friction coefficient (Cf) is evaluated using the Colebrook factor56. The convective wall heat transfer (qw) is modelled using the Colburn correlation57.
To simulate the rupture, we use a numerical methodology previously applied to flow pipe breaks in a pressurized water reactor. As per previous applications, a very fine mesh of 10−5 m is used at the break side. From this point, the mesh size is gradually increased with a 1.05 adjacent cell size ratio up to 500 m, and then is kept constant until the other end. In the initial state, the velocity is zero all along the pipe and the pressure and temperature are initialized at their initial values. At the rupture location point, the pressure drops from the initial pressure to the outlet pressure (hydrostatic pressure at the seafloor) value in 10−3 s. To minimize the computation time, the time step at the beginning of the rupture is set to 10−5 s and progressively increased to 104 s. This procedure is applied to each side of the three pipelines to evaluate the evolution of the total gas flow rate as a function of time.
Sensitivity analysis
We assess uncertainty in our simulations by reperforming the PBREAK and CATHARE simulations using the upper and lower uncertainty bounds for the initial gas temperature, depth of rupture, post-rupture pipeline section lengths and natural gas composition (Extended Data Table 1). As the variables are independent, we sum the resulting deviations from reference emission rates in quadrature to derive the uncertainty at each time step of the simulation. We additionally assess the model uncertainty in CATHARE simulations by varying pipeline roughness, heat transfer coefficients, mesh number and break size (Supplementary Method 1). The CATHARE model uncertainties are summed in quadrature in addition to the uncertainties introduced by the model variables. We do not assess the model uncertainty in PBREAK as this functionality is not accessible to users of the software.
NAER and NAE
We calculate the rate of CH4 emission expected to directly reach the atmosphere (NAER) from each pipeline (NSx) over time, according to equation (5):
$$\rmX\text-\rmNAER_\rmNSx=r_\rmNSx,t-d_\rmNSx,t$$
(5)
where X- is the simulation (P- for PBREAK and C- for CATHARE), t is the simulation time step, n is the total number of simulation time steps, r is the pipeline CH4 emission rate (t h−1), and d is the CH4 dissolution rate9 for the equivalent simulation time step (t h−1). We compute equation (5) over the lower and upper uncertainty bounds of the pipeline emission rates to derive lower and upper bounds of P-NAERNSx and C-NAERNSx. In our paper, we use P-NAERNSx for comparison with top-down atmospheric emission-rate estimates because the pipeline emission rates derived from PBREAK modelling align better with timelines reported by the pipeline operators38 and leak site observations (A. Sundberg, personal communication). The cumulative sum of net atmospheric emissions for each pipeline and pipeline emission-rate simulation (P-NAENSx and C-NAENSx, in kt of CH4) is calculated using equation (6):
$$\rmX\text-\rmNAE_\rmNSx=\mathop\sum \limits_t=1^n(r_\rmNSx,t-d_\rmNSx,t)$$
(6)
We sum the atmospheric CH4 emissions from all three pipeline leaks to derive P-NAEAll and C-NAEAll.
Inversion 1
Inversion 1 is derived from the reanalysis of a previous inversion14 (Supplementary Table 1). Briefly, IASI XCH4 data retrievals58,59 are combined with simulated mixing ratios produced by the TOMCAT offline chemical transport model60 in an inversion framework to optimally quantify the flux rate from the leaks. A global model simulation is carried out covering the period of 26–30 September 2022. The model’s horizontal resolution is approximately 1° × 1°, with 60 vertical levels between the surface and 0.1 hPa. The model dynamical time step is 5 min. The model is initialized with CH4 mixing ratios from ref. 61, which are optimized in the inversion. The fluxes of CH4 from sources other than the Nord Stream leaks are also based on that study, as are the atmospheric loss rates.
Here, both P-NAERNSx and C-NAERNSx and their uncertainties are used as priors in the inversions. Leak flux rates in each emission window (the first 5 min of each leak, the remainder of the first hour and then subsequent 3-h periods) are treated as constant within that window. To drive model transport, meteorological data from the European Centre for Medium-range Weather Forecasts (ECMWF) operational analyses are applied at the same horizontal resolution as the model. In total, we perform eight inversions using the P-NAERNSx and C-NAERNSx priors, with each one optimized against all individual IASI retrievals, or alternatively optimized against the mean XCH4 value in the region of the observed plume, with prior error covariances also tested. Our estimate represents the range across these eight inversions.
Inversion 2
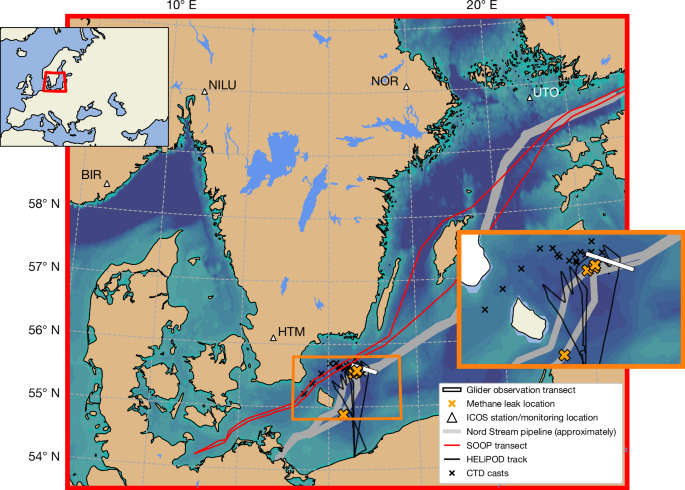
Inversion 2 is derived from the reanalysis of a previous inversion18 (Supplementary Table 1), using CH4 concentrations from three ICOS stations (BIR, NOR and ZEP)62,63,64 and the Norwegian Institute for Air Research (NILU) between 26 and 30 September 2022. The Lagrangian Particle Dispersion Model FLEXPART65 is used to model atmospheric transport and is driven by meteorological data obtained from the ECMWF Integrated Forecasting System. A synthesis inversion approach assuming Gaussian errors is employed for the inverse modelling66. CH4 enhancements are derived by subtracting the average of time-series CH4 concentrations immediately before and after the plume passed at each station. We assemble the CH4 enhancements in an observation vector y and corresponding hourly emission rates into a state vector x and solve for the optimal estimation of x by minimizing the cost function J(x) in equation (7):
$$J(x)=(x-x_\rmb)^\rmTB^-1(x-x_\rmb)+(Hx-y)^\rmTR^-1(Hx-y)$$
(7)
where xb is the prior estimate, T denotes the operation of matrix transposition, B is the prior error covariance matrix, H is the Jacobian matrix operator constructed using FLEXPART transport simulations, y is the concentration enhancement with respect to the background, and R is the observational covariance matrix. The optimal solution to equation (7) (\(\widehatx\)) is given by:
$$\widehatx=x_\rmb+BH^\rmT(HBH^\rmT+R)^-1(y-Hx_\rmb)$$
(8)
The previous estimate18 used wind data at 1° resolution, and xb were derived by modelling flow rates from the depressurization based on initial reports of the pipeline volume, temperature, and pressure in the NS2A pipeline2. Here we use wind data at 0.2° resolution and both P-NAERNSx and C-NAERNSx for xb. Both forwards and backwards simulations are used. Error correlations of 10% for R are used for the inversions based on forward simulations, with no off-diagonal entries being non-zero. Simulations are produced for the transport operator H in forward mode at different resolutions. To account for the uncertainty in the prior, we perform six inversions using the upper, central and lower bounds of P-NAERNSx and C-NAERNSx. In addition, we estimate transport uncertainty using a variant of the statistical technique of resampling. We perform an initial inversion using all available time series for each station and then subsample the stations to obtain inversions using the same inversion parameters. We report the range across estimates derived using this approach.
Inversion 3
Inversion 3 is derived using CH4 concentrations from four ICOS stations (BIR, NOR, HTM and UTO)62,67,68,69 and the NILU between 26 September and 1 October 2022. We use the numerical weather prediction (NWP) model Icosahedral Non-hydrostatic Aerosols and Reactive Trace gases (ICON-ART)70,71 to model atmospheric transport. The model is run in limited area mode with 6.5-km resolution and initialized with NWP analysis fields. Using P-NAERNSx as the prior, we model the three-dimensional CH4 concentration field resulting from the leaks and compare hourly outputs with observations from the ICOS and NILU sites.
Owing to meteorological uncertainty, the timing of modelled and observed plume arrival differs. To allow for this uncertainty, the modelled signals from the leaks are integrated in time for each of the 5 measurement stations (mi, where i = 1, …, 5). The observed signals (oi, where i = 1, …, 5) are obtained analogously after subtracting the background from each observation time series. This background and its uncertainty are estimated for each station using the average and standard deviation of the September observations before arrival of the plume. Because the concentration scales with the emissions, an emission scaling factor is calculated for each station (si) as:
$$s_i=\fraco_im_i$$
(9)
Our posterior emissions estimate pi is derived by:
$$p_i=s_i\times e(t)$$
(10)
where e(t) is the time dependent P-NAERNSx.
Ideally, the scaling factors for all stations would agree, but they differ, probably because of a plume location error. To capture a wide range of plausible meteorological variability, we use an ICON-ART ensemble of 40 members and an additional deterministic run. The ensemble is constructed using operational weather forecasting methods and represents 40 slightly different, equally likely, meteorological initial conditions (k). The scaling factors derived from the ensemble members vary substantially. The minimum emission scaling needed to match the observed with the modelled integrated plume signal at a station is given by si = min(si, k (where k = 1, …, 40)). This way, the dominant meteorological uncertainty is regarded by providing lower bounds for the emissions at each station. Owing to the high response of concentration distribution to the meteorological uncertainty, there are cases where the modelled signal is close to zero owing to location error and scaling factors grow to infinity. Therefore, no upper bound can be derived.
Uncertainties aside from the meteorology are regarded as follows. For each ensemble member, the uncertainty of the prior emissions is propagated to mi by distinguishing the contributions of emissions from 14 time intervals. The uncertainty of each contribution to mi is bounded by the maximum relative prior uncertainty within the respective time interval. Summing these contributions yields upper bounds on the uncertainties of mi between 1% and 10%, depending on which part of the plume is observed. Here, the P-NAERNSx emission profiles representing the prior uncertainty are normalized to the total emissions because the inversion result is independent of the total prior emissions. A higher uncertainty of 6% to 34% is obtained for observations oi due to the background subtraction.
Our emissions estimate is the highest minimum pi derived across the measurement stations (in this case, BIR) rounded to the nearest 10 kt of CH4. Given the time dependency of emissions e(t) and allowing for meteorological transport uncertainty as used in NWP methods, this approach can only derive a lower bound of atmospheric emissions.
Inversion 4
Inversion 4 is derived from the reanalysis of a previous inversion8 (Supplementary Table 1), using CH4 concentrations from four ICOS stations (BIR, NOR, HTM and UTO)62,63,69,72 between 26 September and 1 October 2022. We use the Stochastic Time-Inverted Lagrangian Transport model (STILT)73,74 to model atmospheric transport. The STILT simulation is driven by 0.25° × 0.25° global meteorological fields from the National Centers for Environmental Prediction operational Global Forecast System75 analysis. CH4 concentration enhancements at the four stations are computed by subtracting the median of all September observations before 26 September from the time-series observations. The sensitivity of CH4 enhancements at ICOS stations to CH4 emission rates are computed with forward-mode STILT simulations by tracking the surface influence of 500 particles released from two leak points (one for the adjacent NS1A and NS1B leak sites, and one for the NS2A leak site). As for inversion 2, we solve a Bayesian inverse problem to estimate hourly CH4 emission fluxes from the two leak points using equations (7) and (8). The Jacobian matrix H in equations (7) and (8) is the sensitivity derived from the STILT simulations.
In the previous estimate8, xb were assumed to be zero because no credible prior information was available at the time of publication. Here, we use P-NAERNSx for xb. The prior error for the matrix H is considered to be the maximum uncertainty in the P-NAERNSx prior for emission rates >100 t h−1 (about 10%), and the observation error for the matrix R is 30 ppbv. We compute the uncertainty of the posterior estimate \(\hatx\) by analysing the posterior error covariance matrix (\(\widehatS\)) given by equation (11):
$$\hatS=(H^\rmT\times R^-1\times H+B^-1)^-1$$
(11)
Inversion 5
Inversion 5 is derived using CH4 concentrations from three ICOS stations (BIR, NOR and HTM)76,77 between 26 September and 3 October 2022. We model atmospheric transport using the TNO LOTOS–EUROS chemistry transport model78,79 operated at 0.1° × 0.1° resolution. Meteorological fields are derived from the short-range ECMWF forecast. The CH4 concentration signal from non-Nord Stream sources are generated by the LOTOS–EUROS model using the CAMS-REGv5 emission inventory80 for anthropogenic emissions and the Copernicus Atmosphere Monitoring Service global atmospheric composition forecast81 for boundary conditions. Modelled CH4 concentrations from these sources are considered as background from which we derive CH4 enhancements from the leaks.
We produce two LOTOS–EUROS simulations using P-NAERNSx and C-NAERNSx, including their uncertainty, as the prior. Each simulation results in a total of 35 runs for each NS1 leak and 40 runs for the NS2A leak, leading to a total of 110 runs. For each simulation, a fitting routine is applied to derive an emissions estimate. The fitting is described by an Ax = B system, where A is the source receptor relations, x is the hourly emission enhancement and B is the hourly measurements from the three ICOS stations. The matrix A contains the concentrations simulated in each of our runs at the location of the three ICOS towers. The Ax = B system is underdetermined, and therefore a least-square fit is derived for x such that Ax is as close to B as possible. When the emission enhancements in x are multiplied with the initial emission strengths an estimate for the total emissions is obtained. The estimate uncertainty is the standard deviation across the fittings.
Inversion 6
Inversion 6 is derived from the reanalysis of previous inversions16,17 (Supplementary Table 1), using the temporal variation of CH4 concentrations from two ICOS stations (BIR and NOR)62,63 between 26 September and 3 October 2022. We conduct atmospheric transport simulations using the CHIMERE chemistry transport model82, with 0.2° horizontal resolution and vertical resolution divided into 29 vertical levels from the surface up to 300 hPa. Our CHIMERE simulations are driven by the Community Inversion Framework83. The meteorological fields are interpolated at the model resolution and are derived from 3-hourly operational forecasts sourced from ECMWF at a resolution of 0.15°. The CH4 concentration signal from non-Nord Stream sources is simulated using a standard regional configuration. Anthropogenic emissions other than Nord Stream are derived from EDGARv684 at 0.1° × 0.1° resolution. For natural emissions, such as natural fluxes from peatlands, inundated and mineral soils are taken from the JSBACH-HIMMELI model85. Geological emissions are a climatology based on ref. 86 and GCP-CH4 and scaled down to a global total of 15 Tg of CH4 in accordance with the maximum suggested by ref. 87. Ocean CH4 fluxes are a climatology based on ref. 88. Background concentrations at the side of the area-limited domain of CHIMERE are interpolated from the Copernicus Atmosphere Monitoring Service CH4 reanalysis89.
The previous estimates used a constant emission prior16, and an assumed exponential emission prior17. Our reanalysis uses C-NAERNSx as the emission prior. To ensure the posterior estimates are not biased by the confidence we have with C-NAERNSx values, we use C-NAERNSx temporal profiles and not the value of the rate. To do so, we carry out Monte Carlo simulations by multiplying the emission rate from C-NAERNSx by a random coefficient between 0 and 1.5. This allows to cover the lower and upper bounds of the C-NAERNSx priors. To account for uncertainties from meteorological data, we integrate 11 meteorological datasets from the ECMWF ensemble forecast. The 11 members from the ensemble forecast represent data slightly deviated from a standard case. In addition, CATHARE modelling indicates that the gas velocity exceeds 55 m s−1 during the first 24 h of at all leak sites. For that same period, gas temperatures did not exceed −35 °C owing to localized depressions between the pressure inside and outside the pipelines. Accordingly, we use the analytical solutions for turbulent buoyant plumes from circular sources to estimate the altitude the gas reached before dispersion.
To estimate atmospheric CH4 emissions, we generate 10,000 distinct scenarios. Each scenario is created by picking a random meteorological dataset from the 11 members and an altitude from 10 values between 0 m and 2,000 m for each day of the leaks. Finally, for each scenario, a reduction factor randomly fixed between 0 and 1.5 is assigned. For each scenario, we compute a probability expressing how much the scenario is close to the observations. Within the Bayesian data assimilation process, we evaluate the probability of the reduction coefficient knowing the probability of the scenario. The Bayesian probability is expressed as:
$$P(x| \,y)\,\propto \,P(\,y| x)\,\times \,P(x)\,\times \,P(\rmalt| x)$$
(12)
where x is the reduction coefficient, alt is the altitude reached by the gas, and y is the comparison between the simulations and the observations for the selected stations. P(x|y) is assimilated to the posterior that we want to estimate, P(x) is the emission prior and P(alt|x) is the probability to reach an altitude knowing the rate. To evaluate equation (12), we use the analytical solutions for turbulent buoyant plumes from circular sources. The Bayesian data assimilation allows us to estimate the range and maximum probability of our posterior estimate.