Mapping the ionosphere with millions of phones

Data collection and outlier rejection

The phone measurements used in this work are from a population of Android devices that have location and relevant settings enabled and are using satellite signals to determine location. Android periodically collects sensor measurement data from this population of Android devices to provide and improve location-based services. This collection is limited to conserve battery, memory and network use. More information about Android’s collection and use of location data is available at https://policies.google.com/technologies/location-data.

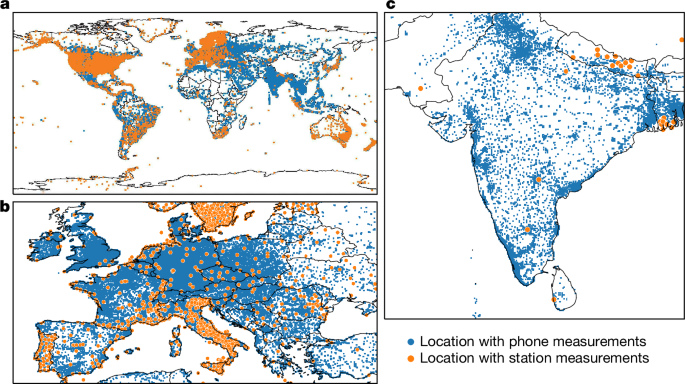
Our research used the collected measurements to make ionospheric TEC maps that can improve location accuracy. For this feasibility study, we used a subset of the collection with daytime satellite measurements (05:00–22:00 local time) and latency up to several days. For simplicity, we limited our analysis to measurements of US GPS and European Galileo constellations at frequencies of 1,575 MHz and 1,176 MHz (known as L1 and L5), accounting for 70% of dual-frequency phone measurements. With these restrictions, we used measurements from between 200,000 and 2 million unique phones per hour, significantly larger than the approximately 9,000 monitoring stations available in the Madrigal database. Our dataset included measurements from about 40 million dual-frequency phones each day.

TEC is a measure of the integral of free-electron density along the straight-line path between a satellite and a phone. We adopted a standard thin-shell model of the ionosphere at a height of 350 km above Earth, allowing us to combine measurements along different paths based on where they intersect the shell, the so-called ionosphere piercing point.

Determining the path taken by the radio signal through the ionosphere requires positions of both the satellite and the phone. Whereas accurate satellite positions are available from published orbit parameters, phone position is calculated by the GNSS receiver in the phone. To maintain user privacy, we used only the location of each phone coarsened to an approximately 10-km grid, and we removed isolated phones with locations far from populated areas. Although this limits the resolution of features in our calculated TEC map, we see that this is still sufficient for resolving the small-scale ionospheric features necessary for location-accuracy improvement and for observations of scientific phenomena.

Although dedicated GNSS receivers reduce the noise in the calculated TEC using an additional measurement of the carrier phase¹⁹, this carrier phase is often unavailable or too noisy in phone receivers. Instead, measurements were collected with a frequency of up to 1 Hz and were aggregated using an uncertainty weighted average over a 1-minute window. Time windows with fewer than ten measurements were dropped.

When solving the linear system to yield the ionospheric VTEC in each cell and the DCB of each phone, some receivers or ionosphere cells are poorly constrained. These phones and cells were removed so that the calculation could proceed without regularization. The calculation is also sensitive to outlier measurements so we filtered these in advance by removing measurements more than 300 TECU from the median for that phone and constellation (about 0.4% of the phone measurements).

Exploiting blockwise structure

Estimating VTEC requires solving a system of linear equations of the form

where VTEC_true and DCB_phone are unknown. As each phone has a unique bias for each satellite constellation, we must jointly fit thousands of ionospheric parameters and millions of bias terms. We do this by minimizing the squared error:

where y = STEC_measured − DCB_satellite, x is a vector containing both ionospheric parameters and phone bias values, and M encodes the linear relationship between these quantities. In this case, M is a sparse matrix and takes the form

The matrix R has shape n × r, where n is the number of measurements and r is the number of ionospheric parameters—in this case, corresponding to tens of thousands of S2 cells. The matrix S has shape n × s, where s is equal to the number of (phone, constellation) pairs in the dataset, as each phone has a unique bias for each constellation.

Solving the least-squares problem amounts to exactly solving the linear system

where T indicates matrix transpose. Using the structure described above, we have

A has the shape r × r, where r is on the order of tens of thousands. It is sparse, having non-zero entry in position ij only when there is a receiver that sees both S2 cells i and j. In this sense, it is a kind of incidence matrix between S2 cells. In particular, A is tractable to invert and apply.

The matrix B is a weighted incidence matrix between S2 cells and receivers with shape r × s, and is short and wide.

D has shape s × s, where s is potentially in the millions. However, S has only one non-zero entry per line, corresponding to the bias of the (receiver, constellation) pair for the particular measurement. As a result, D is diagonal and can be inverted and applied trivially.

We can now apply the blockwise matrix inversion identity

If we are interested only in extracting ionospheric parameters and not the biases for each individual receiver, then we need only consider the terms from the first row of this equation and we get

P = A − BD^−1B^T is known as the Schur complement of D. It has size r × r and is tractable to invert, whereas D is diagonal and is trivial to invert.

In addition to solving for the maximum likelihood value for each coefficient, we would also like to estimate the variance associated with each coefficient. The variance of the solution x is given by

As we are only interested in the covariance of the ionosphere coefficients, we can take the upper left portion of this covariance matrix:

In particular, we are interested in the diagonal elements, as these are the variances of the individual coefficients. However, this is still a large sparse matrix and we would like to avoid materializing it and inverting it directly just to obtain the diagonal. Instead, we use an unbiased estimator for the diagonal of a matrix:

where v is a vector-valued random variable whose entries are drawn uniformly from {+1, −1}, and the asterisk denotes entry-wise multiplication. This approximation generalizes the well-known Hutchinson trace estimator³⁸. To see that this is an unbiased estimator, we first note that

We can now compute the expectation of the jth element of the estimator:

as required. To reduce the variance of this estimate, we apply the procedure to a large number of randomly sampled vectors v and take the average. This allows the ionospheric VTEC and the uncertainty to be estimated from a large number of phone measurements efficiently.

Comparison with monitoring station measurements

Phone measurements and monitoring stations generally agree, but disagreements also exist and are discussed in this section. We compared with monitoring station line-of-sight STEC measurements from the Madrigal database²³. We computed the phone-based STEC estimate for each line of sight from the map using the VTEC at the piercing point and the slant angle to convert to STEC.

One possible source of disagreements is the conversion of the phone-generated VTEC to STEC. This conversion process assumes that the ionosphere is a two-dimensional thin shell at 350 km altitude. This modelling assumption allows the STEC to be computed for some lines of sight not measured by phones if the VTEC at the piercing point has been measured along a different line of sight. The Madrigal dataset also applies a thin-shell assumption (for bias calibration), but there may be small differences in how Earth’s curvature and electron-density profiles are accounted for when applying the zenith-angle correction to convert STEC to VTEC.

In some places and times, the phone-based VTEC estimate is particularly uncertain. Phone measurements are noisy, so a large number must be averaged to get a reliable estimate. In some cases, averaging a few noisy measurements results in a negative (non-physical) VTEC estimate. In addition, the linear system for VTEC and receiver DCBs is poorly constrained when the baselines separating receivers on the ground are short, leading to piercing points being measured at a narrow range of slant angles. Maps can also be poorly constrained when few receivers are making measurements to few satellites. These poorly constrained regions shift over time as the geometry of satellites and receivers changes. Fortunately, our method also provides an uncertainty for each VTEC estimate, and these situations can be distinguished by their large uncertainty. VTEC estimates with standard deviation larger than √50 TECU are excluded from the maps. Extended Data Fig. 3 shows an example of a disagreement between phone-based maps and station measurements with high uncertainty in the phone-based map, indicating that the phone-based map is unreliable in this region.

GNSS measurements are sometimes biased by an effect known as multipath¹⁹. This occurs when the radio signal reaches the receiver by two or more paths and is commonly caused by reflections from the ground or buildings. Phones are more susceptible to this than monitoring stations owing to their complex operating environments. We tried removing multipath measurements but found that the detection methods were unreliable.

Any of these issues could explain the bias shown in Fig. 3 for the quantitative comparison of monitoring station measurements with the ionosphere TEC derived from phone measurements. Similar magnitudes of TEC bias have also been observed in other measurement methods, such as lightning and satellite altimetry, and among the various global ionosphere models^25,26.

Location-accuracy improvement

The primary aim of this work was to improve the location accuracy for Android users by providing more accurate corrections for ionospheric effects. We evaluated the difference in the horizontal location accuracy when different ionospheric models are used by applying the dilution of precision technique³⁹ on a held-out set of phones. To form a baseline for comparison, we also evaluated two published TEC models: a global ionospheric TEC model from the NASA Jet Propulsion Laboratory (JPL)³ and the Klobuchar model⁷.

The Klobuchar model was developed in the early days of GPS and was optimized for the limited computation and bandwidth available at the time. It uses only eight parameters that are broadcast by the satellite and updated daily. The Klobuchar model is still used in the majority of mobile phones, because it is free, reliably available in real time and easy to use. It is sometimes tightly integrated into GNSS hardware in phones.

The JPL Final model has a latency of approximately 3 days, incorporating measurements from 200 monitoring stations to produce a global map of VTEC for every 2 hours on a grid of 2.5° latitude by 5° longitude using a Kalman filter. This model demonstrates the performance when monitoring station measurements are carefully applied.

Extended Data Fig. 6 shows that when evaluated globally, the TEC model fit on phone measurements provides a similar performance to the JPL model and improved performance compared with the Klobuchar model. When limited to India, where there are far more phone measurements available than monitoring stations, the phone-based model outperforms both the Klobuchar model and the JPL model. Extended Data Fig. 7 shows the spatial distribution of location error, confirming this finding in regions of the world with sparse networks of monitoring stations.

Instruments for ionosphere observation

GNSS receivers on the ground are not the only way to observe the ionosphere. Orbiting satellites also use GNSS receivers to track their position, and the same technique can be used to measure the TEC between low-Earth-orbit (LEO) satellites and navigation satellites. Orbit determination receivers map the TEC above LEO satellite orbits⁴⁰. Radio occultation measures the TEC at opportune moments when radio signal paths pass through the limb of the atmosphere and enter side-looking antennas onboard LEO satellites⁴¹. These LEO satellites may also capture GNSS signals reflected off calm waters or ice on Earth’s surface through GNSS reflectometry techniques to measure the TEC along the reflection signal path⁴². All-sky imagers map the emission of ions and neutral particles in the ionosphere at night and reveal structures in the varying plasma density, both from the ground^43,44 and in space^45,46,47. Incoherent scatter radars⁴⁸, coherent radars⁴⁹ and ionosondes⁵⁰ transmit radio waves and record the incoherent backscatters and coherent reflections from layers in the ionosphere to profile the ionospheric electron-density distributions in the radar field of view. In situ measurements can also be performed by LEO satellites such as COSMIC-2 and Swarm, which measure the plasma density along a trajectory inside the ionosphere^51,52.