Longer scans boost prediction and cut costs in brain-wide association studies

Datasets, phenotypes and participants

Following previous studies, we considered 58 HCP phenotypes^59,60 and 36 ABCD phenotypes^15,39. We also consider a cognition factor score derived from all phenotypes from each dataset³¹, yielding a total of 59 HCP and 37 ABCD phenotypes (Supplementary Table 4).

In this study, we used resting-state fMRI from the HCP WU-Minn S1200 release. We filtered participants from a previously reported set of 953 participants⁶⁰, excluding participants who did not have at least 40 min of uncensored data (censoring criteria are discussed in the ‘Image processing’ section) or did not have the full set of the 59 non-brain-imaging phenotypes (hereafter, phenotypes) that we investigated. This resulted in a final set of 792 participants of whom the demographics are described in Supplementary Table 5. The HCP data collection was approved by a consortium of institutional review boards (IRBs) in the USA and Europe, led by Washington University in St Louis and the University of Minnesota (WU-Minn HCP Consortium).

We also considered resting-state fMRI from the ABCD 2.0.1 release. We filtered participants from a previously reported set of 5,260 participants¹⁵. We excluded participants who did not have at least 15 min of uncensored resting-fMRI data (censoring criteria are discussed in the ‘Image processing’ section) or did not have the full set of the 37 phenotypes that we investigated. This resulted in a final set of 2,565 participants of whom the demographics are described in Supplementary Table 5. Most ABCD research sites relied on a central IRB at the University of California, San Diego, for the ethical review and approval of the research protocol, while the others obtained local IRB approval.

We also used resting-state fMRI from the SINGER baseline cohort. We filtered participants from an initial set of 759 participants, excluding participants who did not have at least 10 min of resting-fMRI data or did not have the full set of the 19 phenotypes that we investigated (Supplementary Table 4). This resulted in a final set of 642 participants of whom the demographics described in Supplementary Table 5. The SINGER study has been approved by the National Healthcare Group Domain-Specific Review Board and is registered under ClinicalTrials.gov (NCT05007353) with written informed consent obtained from all participants before enrolment into the study.

We used resting-state fMRI from the TCP dataset. We filtered participants from an initial set of 241 participants, excluding participants who did not have at least 26 min of resting-fMRI data or did not have the full set of the 19 phenotypes that we investigated (Supplementary Table 4). This resulted in a final set of 194 participants of whom the demographics are described in Supplementary Table 5. The participants from the TCP study provided written informed consent following guidelines established by the Yale University and McLean Hospital (Partners Healthcare) IRBs.

We used resting-state fMRI from the MDD dataset. We filtered participants from an initial set of 306 participants. We excluded participants who did not have at least 23 min of resting-fMRI data or did not have the full set of the 20 phenotypes that we investigated (Supplementary Table 4). This resulted in a final set of 287 participants of whom the demographics are described in Supplementary Table 5. The MDD dataset was collected from multiple rTMS clinical trials, and all data were obtained at the pretreatment stage. These trials include ChiCTR2300067671 (approved by the Institutional Review Boards of Beijing Anding Hospital, Henan Provincial People’s Hospital, and Tianjin Medical University General Hospital); NCT05842278, NCT05842291 and NCT06166082 (all approved by the IRB of Beijing HuiLongGuan Hospital); and NCT06095778 (approved by the IRB of the Affiliated Brain Hospital of Guangzhou Medical University).

We used resting-state fMRI from the ADNI datasets (ADNI 2, ADNI 3 and ADNI GO). We filtered participants from an initial set of 768 participants with both fMRI and PET scans acquired within 1 year of each other. We excluded participants who did not have at least 9 min of resting-fMRI data or did not have the full set of the six phenotypes that we investigated (Supplementary Table 4). This resulted in a final set of 586 participants of whom the demographics are described in Supplementary Table 5. The ADNI study was approved by the IRBs of all participating institutions with informed written consent from all participants at each site.

Moreover, we considered task-fMRI from the ABCD 2.0.1 release. We filtered participants from a previously described set of 5,260 participants¹⁵. We excluded participants who did not have all three task-fMRI data remaining after quality control, or did not have the full set of the 37 phenotypes that we investigated. This resulted in a final set of 2,262 participants, of whom the demographics are described in Supplementary Table 5.

Image processing

For the HCP dataset, the MSMAll ICA-FIX resting state scans were used⁶¹. Global signal regression (GSR) has been shown to improve behavioural prediction⁶⁰, so we further applied GSR and censoring, consistent with our previous studies^16,60,62. The censoring process entailed flagging frames with either FD (framewise displacement) > 0.2 mm or DVARS (differential variance) > 75. The frames immediately before and after flagged frames were marked as censored. Moreover, uncensored segments of data consisting of less than five frames were also censored during downstream processing.

For the ABCD dataset, the minimally processed resting state scans were used⁶³. Processing of functional data was performed consistent with our previous study³⁹. Specifically, we additionally processed the minimally processed data with the following steps. (1) The functional images were aligned to the T1 images using boundary-based registration⁶⁴. (2) Respiratory pseudomotion filtering was performed by applying a bandstop filter of 0.31–0.43 Hz (ref. ⁶⁵). (3) Frames with FD > 0.3 mm or DVARS > 50 were flagged. The flagged frame, as well as the frame immediately before and two frames immediately after the marked frame were censored. Furthermore, uncensored segments of data consisting of less than five frames were also censored. (4) Global, white matter and ventricular signals, six motion parameters and their temporal derivatives were regressed from the functional data. Regression coefficients were estimated from uncensored data. (5) Censored frames were interpolated with the Lomb–Scargle periodogram⁶⁶. (6) The data underwent bandpass filtering (0.009–0.08 Hz). (7) Lastly, the data were projected onto FreeSurfer fsaverage6 surface space and smoothed using a 6 mm full-width half-maximum kernel. Task-fMRI data were processed in the same way as the resting-state fMRI data.

For the SINGER dataset, we processed the functional data with the following steps. (1) Removal of the first four frames. (2) Slice time correction. (3) Motion correction and outlier detection: frames with FD > 0.3 mm or DVARS > 60 were flagged as censored frames. 1 frame before and 2 frames after these volumes were flagged as censored frames. Uncensored segments of data lasting fewer than five contiguous frames were also labelled as censored frames. Runs with over half of the frames censored were removed. (4) Correcting for susceptibility-induced spatial distortion. (5) Multi-echo denoising⁶⁷. (6) Alignment with structural image using boundary-based registration⁶⁴. (7) Global, white matter and ventricular signals, six motion parameters and their temporal derivatives were regressed from the functional data. Regression coefficients were estimated from uncensored data. (8) Censored frames were interpolated with the Lomb–Scargle periodogram⁶⁶. (9) The data underwent bandpass filtering (0.009–0.08 Hz). (10) Lastly, the data were then projected onto FreeSurfer fsaverage6 surface space and smoothed using a 6 mm full-width half-maximum kernel.

For the TCP dataset, the details of data processing can be found elsewhere⁶⁸. In brief, the functional data were processed by following the HCP minimal processing pipeline with ICA-FIX, followed by GSR. The processed data were then projected onto MNI space.

For the MDD dataset, we processed the functional data with the following steps. (1) Slice time correction. (2) Motion correction. (3) Normalization for global mean signal intensity. (4) Alignment with structural image using boundary-based registration⁶⁴. (5) Linear detrending and bandpass filtering (0.01–0.08 Hz). (6) Global, white matter and ventricular signals, six motion parameters and their temporal derivatives were regressed from the functional data. (7) Lastly, the data were then projected onto FreeSurfer fsaverage6 surface space and smoothed using a 6 mm full-width half-maximum kernel.

For the ADNI dataset, we processed the functional data with the following steps. (1) Slice time correction. (2) Motion correction. (3) Alignment with structural image using boundary-based registration⁶⁴. (4) Global, white matter and ventricular signals, six motion parameters, and their temporal derivatives were regressed from the functional data. (5) Lastly, the data were then projected onto FreeSurfer fsaverage6 surface space and smoothed using a 6 mm full-width half-maximum kernel.

We derived a 419 × 419 RSFC matrix for each participant of each dataset using the first T minutes of scan time. The 419 regions consisted of 400 parcels from the Schaefer parcellation³⁰, and 19 subcortical regions of interest⁶⁹. For the HCP, ABCD and TCP datasets, T was varied from 2 to the maximum scan time in intervals of 2 min. This resulted in 29 RSFC matrices per participant in the HCP dataset (generated from using the minimum amount of 2 min to the maximum amount of 58 min in intervals of 2 min), 10 RSFC matrices per participant in the ABCD dataset (generated from using the minimum amount of 2 min to the maximum amount of 20 min in intervals of 2 min) and 13 RSFC matrices per participant in the TCP dataset (generated from using the minimum amount of 2 min to the maximum amount of 26 min in intervals of 2 min).

In the case of the MDD dataset, the total scan time was an odd number (23 min), so T was varied from 3 to the maximum of 23 min in intervals of 2 min, which resulted in 11 RSFC matrices per participant. For SINGER, ADNI and ABCD task-fMRI data, as the scans were relatively short (around 10 min), T was varied from 2 min the maximum scan time in intervals of 1 min. This resulted in 9 RSFC matrices per participant in the SINGER datasets (generated from using the minimum amount of 2 min to the maximum amount of 10 min), 8 RSFC matrices per participant in the ADNI datasets (generated from using the minimum amount of 2 min to the maximum amount of 9 min), 9 RSFC matrices per participant in the ABCD N-back task (from using the minimum amount of 2 min to the maximum amount of 9.65 min), 11 RSFC matrices per participant in the ABCD SST task (from using the minimum amount of 2 min to the maximum amount of 11.65 min) and 10 RSFC matrices per participant in the ABCD MID task (from using the minimum amount of 2 min to the maximum amount of 10.74 min).

We note that the above preprocessed data were collated across multiple laboratories and, even within the same laboratory, datasets were processed by different individuals many years apart. This led to significant preprocessing heterogeneity across datasets. For example, raw FD was used in the HCP dataset because it was processed many years ago, while the more recently processed ABCD dataset used a filtered version of FD, which has been shown to be more effective. Another variation is that some datasets were projected to fsaverage space, while other datasets were projected to MNI152 or fsLR space.

Prediction workflow

The RSFC generated from the first T minutes was used to predict each phenotypic measure using KRR¹⁶ with an inner-loop (nested) cross-validation procedure.

Let us illustrate the procedure using the HCP dataset (Extended Data Fig. 1). We began with the full set of participants. A tenfold nested cross-validation procedure was used. The participants were divided in ten folds (Extended Data Fig. 1 (first row)). We note that care was taken so siblings were not split across folds, so the ten folds were not exactly the same sizes. For each of ten iterations, one fold was reserved for testing (that is, test set), and the remainder was used for training (that is, the training set). As there were 792 HCP participants, the training set size was roughly 792 × 0.9 ≈ 700 participants. The KRR hyperparameter was selected through a tenfold cross-validation of the training set. The best hyperparameter was then used to train a final KRR model in the training set and applied to the test set. Prediction accuracy was measured using Pearson’s correlation and COD³⁹.

The above analysis was repeated with different training set sizes achieved by subsampling each training fold (Extended Data Fig. 1 (second and third rows)), while the test set remained identical across different training set sizes, so the results are comparable across different training set sizes. The training set size was subsampled from 200 to 600 (in intervals of 100). Together with the full training set size of approximately 700 participants, there were 6 different training set sizes, corresponding to 200, 300, 400, 500, 600 and 700.

The whole procedure was repeated with different values of T. As there were 29 values of T, there were in total 29 × 6 sets of prediction accuracies for each phenotypic measure. To ensure robustness, the above procedure was repeated 50 times with different splits of the participants into ten folds to ensure stability (Extended Data Fig. 1). The prediction accuracies were averaged across all test folds and all 50 repetitions.

The procedure for the other datasets followed the same principle as the HCP dataset. However, the ABCD (rest and task) and ADNI datasets comprised participants from multiple sites. Thus, following our previous studies^31,39, we combined ABCD participants across the 22 imaging sites into 10 site-clusters and combined ADNI participants across the 71 imaging sites into 20 site-clusters (Supplementary Table 5). Each site-cluster has at least 227, 156 and 29 participants in the ABCD (rest), ABCD (task) and ADNI datasets respectively.

Instead of the tenfold inner-loop (nested) cross-validation procedure in the HCP dataset, we performed a leave-three-site-clusters-out inner-loop (nested) cross-validation (that is, seven site-clusters are used for training and three site-clusters are used for testing) in the ABCD rest and task datasets. The hyperparameter was again selected using a tenfold CV within the training set. This nested cross-validation procedure was performed for every possible split of the site clusters, resulting in 120 replications. The prediction accuracies were averaged across all 120 replications.

We did not perform a leave-one-site-cluster-out procedure because the site-clusters are ‘fixed’, so the cross-validation procedure can only be repeated ten times under a leave-one-site-cluster-out scenario (instead of 120 times). Similarly, we did not go for leave-two-site-clusters-out procedure because that will only yield a maximum of 45 repetitions of cross-validation. On the other hand, if we left more than three site clusters out (for example, leave-five-site-clusters-out), we could achieve more cross-validation repetitions, but at the cost of reducing the maximum training set size. We therefore opted for the leave-three-site-clusters-out procedure, consistent with our previous study³⁹.

To be consistent with the ABCD dataset, for the ADNI dataset, we also performed a leave-three-site-clusters-out inner-loop (nested) cross-validation procedure. This procedure was performed for every possible split of the site clusters, resulting in 1,140 replications. The prediction accuracies were averaged across all 1,140 replications.

We also performed tenfold inner-loop (nested) cross-validation procedure in the TCP, MDD and SINGER datasets. Although the data from the TCP and MDD datasets were acquired from multiple sites, the number of sites was much smaller (2 and 5, respectively) than that of the ABCD and ADNI datasets. We were therefore unable to use the leave-some-site-out cross-validation strategy because that would reduce the training set size by too much. We therefore ran a tenfold nested cross-validation strategy (similar to the HCP). However, we regress sites from the target phenotype in the training set, which were then applied to the test set. In other words, our prediction was performed on the residuals of phenotypes after site regression. Site regression was unnecessary for the SINGER dataset as the data were collected from only a single site. The rest of the prediction workflow was the same as the HCP dataset, except for the number of repetitions. As TCP, MDD and SINGER datasets had smaller sample sizes than the HCP dataset, the tenfold cross-validation was repeated 350 times. The prediction accuracies were averaged across all test folds and all repetitions.

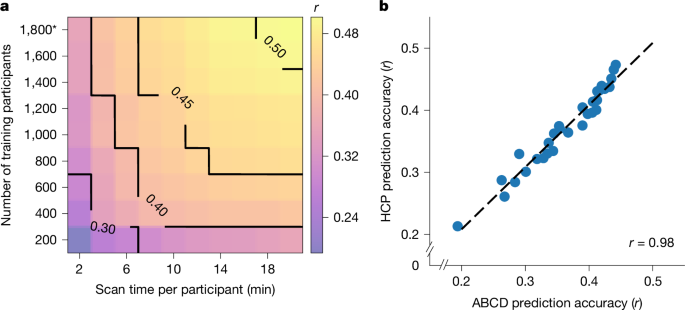
Similar to the HCP, the analyses were repeated with different numbers of training participants, ranging from 200 to 1,600 ABCD (rest) participants (in intervals of 200). Together with the full training set size of approximately 1,800 participants, there were 9 different training set sizes. The whole procedure was repeated with different values of T. As there were 10 values of T in the ABCD (rest) dataset, there were in total 10 × 9 values of prediction accuracies for each phenotype. In the case of ABCD (task), the sample size was smaller with maximum training set size of approximately 1,600 participants, so there were only eight different training set sizes.

The ADNI and SINGER datasets had less participants than the HCP dataset, so we decided to sample the training set size more finely. More specifically, we repeated the analyses by varying the number of training participants from the minimum sample size of 100 to the maximum sample size in intervals of 100. For SINGER, the full training set size is around 580 participants, so there were 6 different training set sizes in total (100, 200, 300, 400, 500 and ~580). For ADNI, the full training set size is around 530, so there were also 6 different training set sizes in total (100, 200, 300, 400, 500 and ~530).

Finally, TCP and MDD datasets were the smallest, so the training set size was sampled even more finely. More specifically, we repeated the analyses by varying the number of training participants from the minimum sample size of 50 to the maximum sample size in intervals of 25. For TCP, the full training set size is ~175, so there 6 training set sizes in total (50, 75, 100, 125, 150 and 175). For MDD, the full training set size is ~258, so there 10 training set sizes in total (50, 75, 100, 125, 150, 175, 200, 225, 250 and 258).

Current best MRI practices suggest that the model hyperparameter should be optimized⁷⁰, so in the current study, we did not consider the case where the hyperparameter was fixed. As an aside, we note that for all analyses, the best hyperparameter was selected using a tenfold cross-validation within the training set. The best hyperparameter was then used to train the model on the full training set. Thus, the full training set was used for hyperparameter selection and for training the model. Furthermore, we needed to select only one hyperparameter, while training the model required fitting many more parameters. We therefore do not expect the hyperparameter selection to be more dependent on the training set size than training the actual model itself.

We also note that our study focused on out-of-sample prediction within the same dataset, but did not explore cross-dataset prediction⁷¹. For predictive models to be clinically useful, these models must generalize to completely new datasets. The best way to achieve this goal is by training models from multiple datasets jointly, so as to maximize the diversity of the training data^72,73. However, we did not consider cross-dataset prediction in the current study because most studies are not designed with the primary aim of combining the collected data with other datasets.

A full table of prediction accuracies for every combination of sample size and scan time per participant is provided in the Supplementary Information.

Fitting the logarithmic model

By plotting prediction accuracy against total scan duration (number of training participants × scan duration per participant) for each phenotypic measure, we observed diminishing returns of scan time (relative to sample size), especially beyond 20 min per participant.

Furthermore, visual inspection suggests that a logarithmic curve might fit well to each phenotypic measure when scan time per participant is 20 min or less. To explore the universality of a logarithmic relationship between total scan duration and prediction accuracy, for each phenotypic measure p, we fitted the function y_p = z_plog₂(t_p) + k_p, where y_p was the prediction accuracy for phenotypic measure p, and t_p is the total scan duration. z_p and k_p were estimated from data by minimizing the square error, yielding \({\hat{z}}_{p}\) and \({\hat{k}}_{p}\).

In addition to fitting the logarithmic curve to different phenotypic measures, the fitting can also be performed with different prediction accuracy measures (Pearson’s correlation or COD) and different predictive models (KRR and LRR). Assuming the datapoints are well explained by the logarithmic curve, the normalized accuracies \(({y}_{p}-{\hat{k}}_{p})/{\hat{z}}_{p}\) should follow a standard log₂(t) curve across phenotypic measures, prediction accuracies, predictive models and datasets. For example, Supplementary Fig. 9a shows the normalized prediction performance of the cognitive factors for different prediction accuracy measures (Pearson’s correlation or COD) and different predictive models (KRR and LRR) across HCP and ABCD datasets.

Here we have chosen to use KRR and linear regression because previous studies have shown that they have comparable prediction performance, and also exhibited similar prediction accuracies as several deep neural networks^16,39. Indeed, a recent study suggested that linear dynamical models provide a better fit to resting-state brain dynamics (as measured by fMRI and intracranial electroencephalogram) than nonlinear models, suggesting that, due to the challenges of in vivo recordings, linear models might be sufficiently powerful to explain macroscopic brain measurements. However, we note that, in the current study, we are not making a similar claim. Instead, our results suggest that the trade-off between scan time and sample size are similar for different regression models, and phenotypic domains, scanners, acquisition protocols, racial groups, mental disorders, age groups, as well as resting-state and task-state functional connectivity.

Fitting the theoretical model

We observed that sample size and scan time per participant did not contribute equally to prediction accuracy, with sample size having a more important role than scan time. To explain this observation, we derived a mathematical relationship relating the expected prediction accuracy (Pearson’s correlation) between noisy brain measurements and non-brain-imaging phenotype with scan time and sample size.

Based on a linear regression model with no regularization and assumptions including (1) stationarity of fMRI (that is, autocorrelation in fMRI is the same at all timepoints), and (2) prediction errors are uncorrelated with errors in brain measurements, we found that

where \(E(\widehat{\rho })\) is the expected correlation between the predicted phenotype estimated from noisy brain measurements and the observed phenotype. K₀ is related to the ideal association between brain measurements and phenotype, attenuated by phenotypic reliability. K₁ is related to the noise-free ideal association between brain measurements and phenotype. K₂ is related to brain–phenotype prediction errors due to brain measurement inaccuracies. Full derivations are provided in Supplementary Methods 1.1 and 1.2.

On the basis of the above equation, we fitted the following function \({y}_{p}={K}_{0,p}\sqrt{\frac{1}{1+{K}_{1,p}/N+{K}_{2,p}/(NT)}}\), where y_p is the prediction accuracy for phenotypic measure p, N is the sample size and T is the scan time per participant. K_0,p,K_1,p and K_2,p were estimated by minimizing the mean squared error between the above function and actual observation of y_p using gradient descent.

Non-stationarity analysis

In the original analysis, FC matrices were generated with increasing time T based on the original run order. To account for the possibility of fMRI-phenotype non-stationarity effects, we randomized the order in which the runs were considered for each participant. As both the HCP and ABCD datasets contained 4 runs of resting-fMRI, we generated FC matrices from all 24 possible permutations of run order. For each cross-validation split, the FC matrix for a given participant was randomly sampled from 1 of the 24 possible permutations. We note that the randomization was independently performed for each participant.

To elaborate further, let us consider an ABCD participant with the original run order (run 1, run 2, run 3, run 4). Each run was 5 min long. In the original analysis, if scan time T was 5 min, then we used all the data from run 1 to compute FC. If scan time T was 10 min, then we used run 1 and run 2 to compute FC. If scan time T was 15 min, then we used runs 1, 2 and 3 to compute FC. Finally, if scan time T was 20 min, we used all 4 runs to compute FC.

On the other hand, after run randomization, for the purpose of this exposition, let us assume that this specific participant’s run order had become run 3, run 2, run 4, run 1. In this situation, if the scan time T was 5 min, then we used all data from run 3 to compute FC. If scan time T was 10 min, then we used run 3 and run 2 to compute FC. If scan time T was 15 min, then we used runs 3, 2 and 4 to compute FC. Finally, if T was 20 min, we used all 4 runs to compute FC.

Optimizing within a fixed fMRI budget

To generate Extended Data Fig. 6, we note that given a particular scan cost per hour S and overhead cost per participant O, the total budget for scanning N participants with T min per participant is given by (T/60 × S + O) × N. Thus, given a fixed fMRI budget (for example, US$1 million), scan cost per hour (for example, US$500) and overhead cost per participant (for example, US$500), we increase scan time T in 1 min intervals from 1 to 200 and, for each value of T, we can find the largest sample size N, such that the scan costs stayed within the fMRI budget. For each pair of sample size N and scan time T, we can then compute the fraction of maximum accuracy based on Fig. 4a.

Optimizing to achieve a fixed accuracy

To generate Figs. 4b,c, 5 and 6, suppose we want to achieve 90% of maximum achievable accuracy, we can find all pairs of sample size and scan time per participant along the 0.9 black contour line in Fig. 4a. For every pair of sample size N and scan time T, we can then compute the study cost given a particular scan cost per hour S (for example, US$500) and a particular overhead cost per participant O (for example, US$1,000): (T/60 × S + O) × N. The optimal scan time (and sample size) with the lowest study cost can then be obtained.

Brain-wide association reliability

To explore the reliability of univariate brain-wide association analyses (BWAS)¹, we followed a previously established split-half procedure^14,15.

Let us illustrate the procedure using the HCP dataset (Supplementary Fig. 20a). We began with the full set of participants, which were then divided into ten folds (Supplementary Fig. 20a (first row)). We note that care was taken so siblings were not split across folds, so the ten folds were not exactly the same sizes. The ten folds were divided into two non-overlapping sets of five folds. For each set of five folds and each phenotype, we computed the Pearson’s correlation between each RSFC edge and phenotype across participants, yielding a 419 × 419 correlation matrix, which was then converted into a 419 × 419 t-statistic matrix. Split-half reliability between the (lower triangular portions of the symmetric) t-statistic matrices from the two sets of five folds was then computed using the intraclass correlation formula^14,15.

The above analysis was repeated with different sample sizes achieved by subsampling each fold (Supplementary Fig. 20a (second and third rows)). The split-half sample sizes were subsampled from 150 to 350 (in intervals of 50). Together with the full sample size of approximately 800 participants (corresponding to a split-half sample size of around 400), there were 6 split-half sample sizes corresponding to 150, 200, 250, 300, 350 and 400 participants.

The whole procedure was also repeated with different values of T. As there were 29 values of T, there were in total 29 × 6 univariate BWAS split-half reliability values for each phenotype. To ensure robustness, the above procedure was repeated 50 times with different split of the participants into 10 folds to ensure stability (Supplementary Fig. 20a). The reliability values were averaged across all 50 repetitions.

The same procedure was followed in the case of the ABCD dataset, except as previously explained, the ABCD participants were divided into ten site-clusters. Thus, the split-half reliability was performed between two sets of five non-overlapping site-clusters. In total, this procedure was repeated 126 times as there were 126 ways to divide 10 site-clusters into two sets of 5 non-overlapping site-clusters.

Similar to the HCP, the analyses were repeated with different numbers of split-half participants, ranging from 200 to 1,000 ABCD participants (in intervals of 200). Together with the full training set size of approximately 2,400 participants (corresponding to a split-half sample size of approximately 1,200 participants, there were 6 split-half sample sizes, corresponding to 200, 400, 600, 800, 1,000, 1,200.

The whole procedure was also repeated with different values of T. As there were 10 values of T in the ABCD dataset, there were in total 10 × 6 values univariate BWAS split-half reliability values for each phenotype.

Previous studies have suggested the Haufe-transformed coefficients from multivariate prediction are significantly more reliable than univariate BWAS^14,15. We therefore repeated the above analyses by replacing BWAS with the multivariate Haufe-transform.

A full table of split-half BWAS reliability for each given combination of sample size and scan time per participant is provided in the Supplementary Information.

Statistical analyses

Supplementary Tables 1–3 summarize all quantifications and statistical analyses performed in this study. When statistical tests were performed, multiple-comparison correction was performed within each result section using Benjamini–Yekutieli FDR correction with q < 0.05 (ref. ⁷⁴).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.