Subjects
Three adult male rhesus monkeys (Macaca mulatta), aged 11, 12 and 8âyears, participated in the experiment. Monkeys A, H and J weighed 11, 14 and 12âkg, respectively. All surgical and experimental procedures were approved by the Stanford University Institutional Animal Care and Use Committee and were in accordance with the policies and procedures of the National Institutes of Health.
Behavioural task
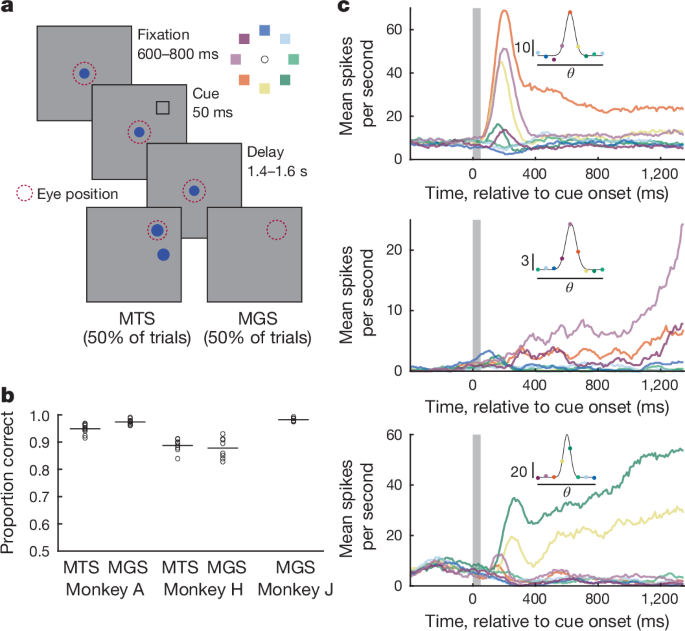
Stimuli were presented on a VIEWPixx3D monitor positioned at a viewing distance of 60âcm using Psychtoolbox and MATLAB (v.R2022a, MathWorks). Eye position was monitored at 1âkHz using an Eyelinkâ1000 eye-tracking system (SR Research). On each trial, the animals were presented with a cue at one of eight possible locations and reported this location after a brief memory delay to receive a fluid reward. Cues were square frames (green for monkeyâA, black for monkeyâH, white for monkeyâJ) measuring 1° of visual angle on a side, and presented at 5â7° of eccentricity (depending on the session).
Monkeys initiated behavioural trials by fixating a central fixation spot presented on a uniform grey background. After the monkeys had maintained fixation for 600â800âms (randomly selected on each trial), a cue appeared for 50âms at one of eight possible locations separated by 45° around fixation. Cue presentation was followed by a delay period that varied randomly from 1,400 to 1,600âms. Following the delay period, the fixation spot disappeared and the animal was presented with one of two possible response screens. On MTS trials, two targets appeared (filled blue circles, radius 1° of visual angle (DVA)): one at the previously cued location and the other at one of the seven remaining non-cued locations. On MGS trials, no targets appeared. In either case, the animals received a reward of juice for making an eye movement to within 5âDVA of the previously cued location and then maintaining fixation for 200âms. MTS and MGS trials were randomly interleaved such that the animals could not predict the trial type. MonkeyâJ was trained on, and performed only, the MGS task. The animals had to maintain their gaze within either 3âDVA (monkeyâA) or 2âDVA (monkeys H and J) from fixation throughout the trial until the response stage. The intertrial interval was 300â1,000âms following each correct response. Failure to acquire fixation, fixation breaks and incorrect responses were not rewarded and were followed by a 2,000âms intertrial interval.
Surgical procedures and recordings
Monkeys were implanted with a titanium headpost to immobilize the head, and with a titanium chamber to provide access to the brain (see ref. 12 for full details). In a previous study66, we identified the frontal eye field based on its neurophysiological characteristics and ability to evoke saccades with electrical stimulation at low currents67. Here we recorded from both areaâ8, within and anterior to the frontal eye field, and the principal sulcus (9/46) (monkeyâA, areaâ8; monkeyâH, areas 8 and 9/46; monkeyâJ, area 9/46), using primate Neuropixels probes39. During each session, we pierced the dura using a screw-driven, 21-gauge pointed cannula and lowered a single probe through this cannula using a combination of custom three-dimensional printed grids and motorized drives (NAN instruments). Probe trajectories spanned several cortical columns, as inferred from the broad distribution of preferred cue locations across neurons. Recordings were allowed to settle for around 30âmin before the start of the experiment, to mitigate drift. We configured probes to record from 384âactive channels in a contiguous block, allowing dense sampling of neuronal activity along a 3.84âmm span.
Neuropixels filter and digitize activity at the headstage separately for the action potential bands (300âHz high-pass filter, 30âkHz sampling frequency) and local field potential (1âkHz low-pass filter, 2.5âkHz sampling frequency). Activity was monitored during experimental sessions and saved to disk using SpikeGLX (https://billkarsh.github.io/SpikeGLX/).
Data preprocessing
Spiking in the action potential band was identified and sorted offline using Kilosort3 (ref. 68). Because we were interested in population-level coding of memory, we analysed both putative single- and multi-unit clusters identified by Kilosort. Spike times were aligned to a digital trigger on each trial, indicating cue onset, and corrected for a lag in stimulus presentation estimated offline using photodiode measurements from the stimulus display and the timing of the cue-evoked response. Neurons that fired fewer than 1,000âspikes in the experimental sessions (each roughly 3âh) were excluded from further analyses. Spike times were converted to smoothed firing rates (sampling interval, 10âms) by representing each spiking event as a delta function and convolving this time series with a 100âms boxcar. For CCG analyses, unsmoothed spikes times were binned with a width and timestep of 1âms. Incorrect trials were rare (Fig. 1b) and were excluded from subsequent analysis. Waveform templates were localized in space using NeuropixelUtilities (https://djoshea.github.io/neuropixel-utils/). Local field potentials (LFPs) were sampled at 2,500âHz. Offline, LFPs were filtered using a 2â200-Hz-bandpass, zero-phase Butterworth, notch filtered at 60âHz and downsampled to 1,000âHz. LFPs were transformed into the time-frequency domain using Morlet wavelets and downsampled to 100âHz.
Statistics and reproducibility
All statistical tests are two-sided unless otherwise specified. Key findings and brainâbehaviour relationships were evident in each of the three animals (Extended Data Figs. 2 and 7), and in each of the 25âindividual experimental sessions (Extended Data Fig. 3). Sample size (three animals, 8,255âneurons) was chosen based on standards in the field. Each animal was exposed to every task manipulation. Within a session, task manipulations were randomized across trials. Neurons were recorded without bias, and electrodes placed to maximize signal-to-noise of the electrophysiological signal.
Functional subtyping
To determine the functional subtype of units69 (Extended Data Fig. 1), we analysed firing rates during three time epochs: visual (0â300âms after cue onset), memory (500â1,400âms after cue onset) and motor (100â300âms post-fixation offset). A unit was labelled as being selective during a given epoch if firing rates during that epoch were significantly modulated by cue location (one-way ANOVA, Pâ<â0.05 criterion). Units were then sorted into functional subclasses based on the set epochs during which each unit was selective.
Classification of cue location
Firing-rate estimates for each unit and time point relative to cue onset were z-scored across trials before classification. We used linear classifiers to quantify the amount of information on the location of the cue in populations of simultaneously recorded units. We held out each trial for test one by one, training a logistic regression classifier (as implemented by fitclinear.m in MATLAB) to predict cue location using the population vector of firing rates. Specifically, classifiers were trained to discriminate the same cue location as the test trial from the opposite cue location, using the applicable subset of trials from the training set. Data were subsampled during training to equalize trial counts for the two conditions. A unique classifier was trained and tested for each time point relative to cue onset. âClassification accuracyâ reflects the proportion of correctly classified test trials (Fig. 2c); âclassifier confidenceâ is the non-thresholded value of the logistic function corresponding to the probability assigned by the classifier to the correct label at test (Fig. 3).
Cross-state classification (Extended Data Fig. 6a) was similar, except that only values from trial time points labelled On or Off (as appropriate) entered the training set or were held out as a test trial. Test confidence values were averaged across the memory delay (500â1,400âms after cue) to yield the final results.
Cross-temporal classification (Fig. 6b) was also similar, except that we used a split-half approach in which the classifiers for each time point were trained on half of the available population of trials and tested (cross-temporally) using the other half.
Mixture modelling of confidence
We used a mixture-modelling approach to test whether confidence during the memory delay (500â1,400âms after cue) was best described as drawn from a one- or a two-state distribution (Extended Data Fig. 5). To do this, for each session and cue location we modelled the probability density function of confidence values during the memory delay as either a single beta distribution,
$$p(c)={\rm{Beta}}(c\,;\alpha ,\beta ),$$
or a mixture of two beta distributions,
$$p(c)=w\times {\rm{B}}{\rm{e}}{\rm{t}}{\rm{a}}(c\,;\alpha ,\beta )+(1-w)\times {\rm{B}}{\rm{e}}{\rm{t}}{\rm{a}}(c\,;{\alpha }^{{\prime} },{\beta }^{{\prime} }),$$
where c is confidence, \(\alpha ,\beta ,{\alpha }^{{\prime} }\) and \({\beta }^{{\prime} }\) parameterize beta distribution(s) and w is the mixing coefficient. The best-fitting parameters of each model were identified by maximum-likelihood estimation using gradient descent in MATLAB. We used fourfold cross-validation on the population of trials to assess the likelihood of each model on held-out test data, and then normalized by the number of trials and changed the log likelihood to baseâ2 to yield the cross-validated score of each model in terms of bits per trial. Finally, we subtracted these two model scores and averaged across conditions to yield the difference in model performance for each session.
Note that our choice of beta distribution here is principled: it is extremely flexible, able to demonstrate a broad range of skewness and kurtosis and naturally accommodates bounded continuous variables such as confidence70. This flexibility makes this analysis conservative, ensuring that the one-state model is capable of describing a broad range of empirical distributions. Nevertheless, results were not dependent on the exact modelling approach: similar results for our one-versus-two-state model comparison were obtained when using either Gaussian mixture or hidden Markov models.
Analysis of microsaccades
The horizontal and vertical eye position records were convolved with a Gaussian kernel (Ïâ=â4.75âms) to suppress noise before taking first derivatives, yielding the eye velocity along each dimension. We then took the root sum of squares of the horizontal and vertical velocities to obtain eye speed. We flagged peaks in this time series with a minimum peak height of 10°âsâ1 and a minimum interpeak distance of 50âms as microsaccades (ref. 71 and Extended Data Fig. 4), which were confirmed by visual inspection of the data.
Labelling of On and Off states
To identify On and Off states (Fig. 4a), we repeated the cue classification analysis described above 50âtimes, randomly shuffling the labels of the training set for each test trial. This yielded, for each trial, a null distribution of 50âconfidence time series (Fig. 4a). We then z-scored each time point of the true confidence time series by the mean and standard deviation of this null distribution. Individually significant (above 1.96) z-values were cluster corrected for multiple comparisons over time72. In brief, we compared the sum of contiguous individually significant z-values with that expected by chance (randomization test). Clusters with a mass greater than the 95% percentile of the null were labelled On states; contiguous z-values falling below a conservative (Pâ>â0.20) threshold for at least five consecutive time points were labelled Off states.
Tuning curves
To test whether On and Off states reflected coordinated changes in tuning across the neural population, we used a split-half approach. First, firing-rate estimates for each unit and time point relative to cue onset were z-scored across trials. Then, for each session, we randomly divided the population of units in half. We used one half of the units to identify On and Off states, as described above. Next, for each unit in the held-out population, we computed mean firing rate during the memory delay for each cue location separately for On and Off states, averaging across relevant time points and across trials. This yielded, for each unit, two eight-element vectorsâthe On and Off tuning functions. To align tuning functions across units, the preferred cue location for each was identified as the condition in which the sum of the On and Off functions was greatest, and assigned an arbitrary value of zero degrees. Alignment of tuning curves to the maximum-valued preferred cue in this way will necessarily produce a peak at zero degrees in the average tuning function, even in the absence of true tuning. To correct for this, for each unit we also computed null On and Off tuning functions by first shuffling cue labels across trials, aligned these to the preferred cue and subtracted them from the true On and Off tuning functions (Fig. 3d).
For demonstration purposes, we fit the average On and Off tuning functions with a difference of Gaussians using gradient descent in MATLAB. Difference of Gaussians is useful for describing tuning curves that show surround suppression73.
Population firing rates
To describe how population firing rates evolved over the course of the trial, we averaged these across all units recorded in the same session and across all trials for the preferred cue location (greatest mean classification confidence during the memory delay), yielding a single time series for each session. We then normalized this time series by the mean and standard deviation of a 400âms baseline period (â400 to 0âms relative to cue onset), yielding a metric of population spiking in units of standard deviations above baseline (Fig. 4e, grey traces). We repeated this analysis for the memory delay, this time including only data points labelled On or Off (Fig. 4e, orange and blue traces).
Phaseâstate relationships
To determine whether the phases of different frequency components of the LFP were predictive of On and Off states, we first extracted the phase from the time-frequency representation of the LFP. Next, we identified the onset time of On and Off states during the memory delay across all trials within a session. Then, for each session, probe channel and frequency (4â60âHz), we computed the (circular) mean phase at On state and Off state onset, and the magnitude of the angular difference between these means. If phase is predictive of state, this difference should be larger than that expected by chance. Accordingly, we obtained a null distribution of phase difference magnitudes by repeating this procedure 1,000âtimes, randomly permuting On and Off labels for each phase measurement on each iteration and used this null distribution to generate a z-score metric. Z-scores were averaged across channels, yielding a phaseâstate metric for each session and frequency of interest. Finally, we tested whether these scores were greater than zero for each frequency of interest (cluster-corrected randomization test).
Standard deviation of background noise
To ensure that changes in recording quality could not account for the presence of On and Off states in our recordings, we measured the standard deviation of background noise42 in the action potential band (0.3â10âkHz). Specifically, for each On and Off state identified using the non-parametric procedure described above, noise standard deviation was estimated as
$${{\sigma }}_{n}={\rm{m}}{\rm{e}}{\rm{d}}{\rm{i}}{\rm{a}}{\rm{n}}\left(\frac{|x|}{0.6745}\right),$$
where x is the time series of raw action potential band values recorded during the state. Noise estimates were averaged across all On and Off states within each session.
Demixed principal components analysis
We used demixed principal components analysis analysis to decompose population activity into different components reflecting cue location, time and their interaction. As with our classification-based analyses, we applied demixed principal components to the smoothed firing rates from each session, focusing on activity during the delay period (500â1,400âms after cue). The proportion of variance explained and components were extracted as described in ref. 50.
Single-neuron ANOVA
We downsampled the smoothed firing rates for each neuron to 100âms steps and modelled firing rate during the delay (500â1,400âms after cue) as a linear combination of cue location, firing rate and their interaction, to estimate the proportion of variance explained by each of these terms.
CCG analysis
To characterize functional connectivity among units, we computed cross-correlations between spike trains of all pairs of simultaneously recorded neurons with mean firing rates greater than 1âHz. CCGs were computed separately for each cue location. Following previous studies46, to mitigate firing-rate effects, we normalized cross-correlation for each pair of neurons by the geometric mean of their firing rates for the cue location condition under consideration. The CCG for a pair of neurons (j, k) in condition c was therefore
$${{\rm{CCG}}(\tau )}_{j,k,c}=\frac{{\sum }_{i=1}^{M}{\sum }_{t=\tau +1}^{N}{x}_{j}^{i}(t-\tau )\times {x}_{k}^{i}(t)}{\sqrt{{\sum }_{i=1}^{M}{\sum }_{t=\tau +1}^{N}{x}_{j}^{i}(t-\tau )\times {\sum }_{i=1}^{M}{\sum }_{t=\tau +1}^{N}{x}_{k}^{i}(t)}},$$
where M is the number of trials collected for cue location c, N is the number of time bins within a trial, \(\tau \) is the time lag between the two spike trains and \({x}_{k}^{i}(t)\) is 1 if neuron j is fired in time bin t of trial i, but zero otherwise.
To correct for correlation due to stimulus locking or slow fluctuations in population response, we subtracted a jittered CCG from the original. This jittered CCG reflects the expected value of the CCG computed from all possible jitters of each spike train within a given jitter window74,75. The jittered spike train preserves both the poststimulus time histogram (PSTH) of the original spike train across trials and the spike count in the jitter window within each trial. As a result, jitter correction removes the correlation between PSTHs (stimulus locking) and those on time scales longer than the jitter window (slow population correlations). We chose a 25âms jitter window, following previous work45,46,76,77.
We classified a CCG as significant if the peak of the jitter-corrected CCG occurred within 10âms of zero and was more than seven standard deviations above the mean of a high-lag baseline period (100 > |\(\tau \)|â>â50)45. Zero-lag CCGs were excluded from the analyses reported here, although their inclusion yielded statistically indistinguishable results.
All CCGs were estimated using spike trains during the memory delay (500â1,400âms after cue) to avoid the influence of visually evoked responses. CCG analyses specific to On and Off states (Fig. 5f) were computed by first setting x(t) to zero for all time points not identified as On or Off (respectively), and then repeating the analysis described above.
Manhattan distance
To determine whether patterns of functional connectivity differed according to the contents of memory, we compared the graphs of significant CCGs across cue locations in a pairwise manner (Fig. 5câf). For each session and cue location, we represented the results of our CCG analyses as a graph in which nodes were units. The edge (connection) between each pair of units was assigned a weight of 1 if the pair had a significant CCG, and zero otherwise. Then, for each possible pair of cue locations, we computed the Manhattan distance, the number of edges with a weight that differed across the two graphs. Finally, we averaged this metric across all 28âpossible pairs of conditions, yielding one summary statistic per session.
To normalize this mean Manhattan distance for comparison across sessions, we shuffled the cue location labels within each pair of neurons for each pair of conditions under consideration across trials, and repeated the entire analysis pipeline 50âtimes (25 for analyses specific to On and Off states), from CCG estimation through Manhattan distance calculation. We then z-scored the mean Manhattan distance for each session by this null distribution and compared these z-scores to zero (Fig. 5f).
Note that CCGs among both single and multi-units have been widely used as a measure of functional connectivity78,79,80,81,82,83,84. Indeed, CCGs based on multi-unit activity may be more sensitive in detection of correlations in spiking than similar analyses of single-neuron pairs78,85,86. Nonetheless, the presence of multi-units in our dataset does limit the conclusions that might be drawn about the specific neuronal subtypes involved in the cue-dependent ensembles that we observeâfor example, putative pyramidal versus non-pyramidal neurons.
Firing-rate-matched control
The geometric mean firing rate of pairs of units varied significantly across the eight cue locations (one-way ANOVA, Pâ=â0.002; Fig. 6a). Geometric mean firing rates were statistically indistinguishable, however, across cue locations 1â4 (Pâ=â0.332) and 5â8 (Pâ=â0.884). Therefore, we repeated the analysis of Manhattan distance described above, this time computing it among only cue locations 1â4 and 5â8 (Extended Data Fig. 6b), to yield a firing-rate-matched variant of the analysis presented in Fig. 5f.
Joint selectivity
To determine the selectivity of units during the evoked response, we averaged each unitâs cue-locked firing rate over time (0â400âms after cue onset), yielding an nTrialsâÃâ1 vector of firing rates. We then performed one-way ANOVA to evaluate the relationship between cue location and firing rate. If the effect of cue location was significant (Pâ<â0.05), the unit was deemed selective to cue location, and the location at which it had the greatest mean firing rate was labelled the preferred location. Pairs of units were deemed jointly selective if they were selective for the same cue location.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.