Interferometric single-shot parity measurement in InAs–Al hybrid devices

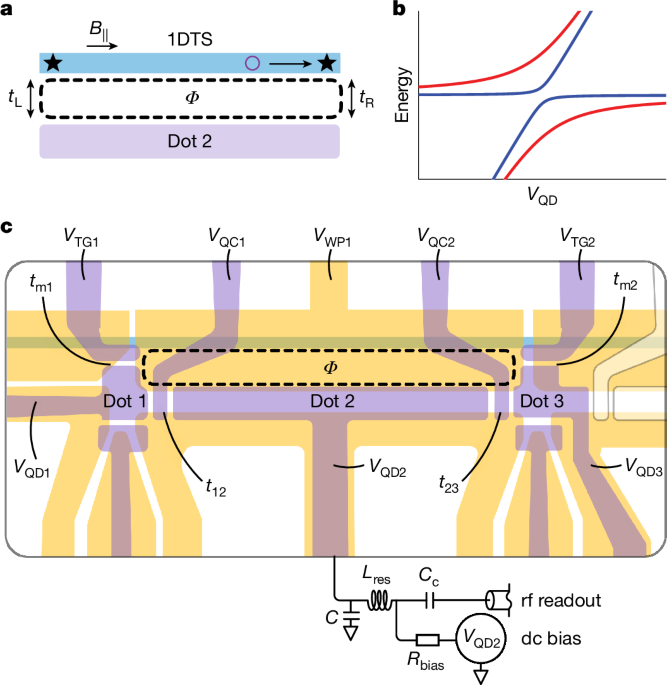
To measure a time record of the fermion parity, we tune up the TQDI and perform a sequence of nearly 1.5 × 10⁴ consecutive measurements of the resonator response, each with an integration time of 4.5 μs, thereby recording a time trace of total length 67 ms. To improve visibility and compare with theoretical predictions, we downsample the time trace by averaging over a 90-μs window. By comparing the measured resonator response with a reference trace (taken with dot 2 in a Coulomb valley), we convert it to a \(\widetildeC_\rmQ\) record, which includes a field-dependent shift of C_Q that cancels out of ΔC_Q (see equation (28) in the Supplementary Information).

We sweep V_QD2 to find charge transitions in dot 2 and, because the normal to the plane of the device is only slightly offset (<1°) from the x axis of the magnet, we sweep the x component of the magnetic field B_x in steps of 0.14 mT to study the dependence on Φ. Our B_x sweep range is offset from 0 so that B_⊥ (which contains a contribution from B_z) is swept symmetrically around 0. We use the topological gap protocol (TGP)¹⁴ to select an in-plane field B_∥ and a wire plunger gate voltage V_WP1 range (indicated, respectively, in Fig. 1a,c) for our measurements, as discussed in Section 4 of the Supplementary Information. The readout system parameters that we achieve are not strongly dependent on these values. For measurement A1 of device A, the relevant regime is B_∥ ≈ 1.8 T and V_WP1 ≈ −1.832 V.

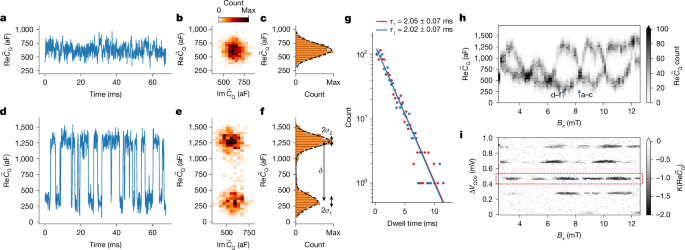
For appropriately tuned quantum dot plungers, in particular for V_QD2 close to resonance, the measured \(\widetildeC_\rmQ\) record exhibits switches between two capacitance values that differ by a ΔC_Q(B_x) that oscillates as a function of B_x. At some B_x, there are no visible switches, as in Fig. 3a, so ΔC_Q(B_x) vanishes. At generic B_x, there is a clear random telegraph signal (RTS), which is shown in Fig. 3d for the B_x that corresponds to maximal ΔC_Q(B_x). From a histogram of all \(\widetildeC_\rmQ\) observed within this time trace, we extract an achieved SNR of 5.01 in 90 μs (Fig. 3e,f) or, equivalently, an SNR of 1 in 3.6 μs (see Section 3.3 of the Supplementary Information). As demonstrated in Fig. 3g, the intervals between switches follow an exponential distribution with a characteristic time τ_RTS ≈ 2 ms. By plotting histograms of the \(\widetildeC_\rmQ\) time traces as a function of B_x, as shown in Fig. 3h, we observe a B_x-dependent bimodal distribution of \(\widetildeC_\rmQ\) values with peaks separated by ΔC_Q(B_x). The oscillation period of ΔC_Q(B_x) is 1.9 ± 0.1 mT, which is consistent with the expected flux of h/2e through the interference loop in this device geometry. We interpret the RTS in C_Q as originating from switches of the fermion parity in the wire; see Section 7.3 of the Supplementary Information for details.

Measurements in device A (measurement A1) in the (B_∥, V_WP1) parameter regime identified through the tune-up procedure discussed in the main text and Section 4 of the Supplementary Information; specifically, V_WP1 = −1.8314 V and B_∥ = 1.8 T. The raw rf signal has been converted to complex \(\widetildeC_\rmQ\) by the method described in Section 3.1 of the Supplementary Information. a,d, Time traces at B_x values corresponding to minimal (panel a) and maximal (panel d) values of ΔC_Q for a fixed choice of V_QD2 close to charge degeneracy. b,e, Histograms of complex \(\widetildeC_\rmQ\) for the time trace shown in panels a and d. c,f, Histograms of the real part \(\rmRe\widetildeC_\rmQ\) with Gaussian fits for an extraction of the SNR = δ/(σ₁ + σ₂) = 5.01, the details of which are given in Section 3.3 of the Supplementary Information. g, Histogram of dwell times aggregated over all values of B_x, in which the signal shows bimodality. Fitting to an exponential shows that the up and down dwell times agree to within the standard error on the fits: 2.05 ± 0.07 ms and 2.02 ± 0.07 ms, respectively. h, Histogram of \(\widetildeC_\rmQ\) values as a function of B_x, showing clear bimodality that is flux-dependent with period h/2e. The vertical arrows indicate the B_x values at which the time traces in panels a and d were taken. i, Kurtosis in the measured quantum capacitance, \(K(\textRe\widetildeC_\rmQ)\), of dot 2 as a function of B_x (which controls Φ) and ΔV_QD2, the change in dot plunger gate voltage from the starting point of the scan (which controls the dot 2 detuning). The dashed red rectangle indicates the ΔV_QD2 value at which the data in the other panels were taken.

The visibility and phase of the oscillations vary between successive charge transitions in dot 2. We illustrate this by showing the kurtosis K(C_Q) (which detects bimodality; see Section 3.2 of the Supplementary Information) of the \(\widetildeC_\rmQ\) time traces for several different charge transitions in Fig. 3i. A similar difference in the visibility of flux-induced oscillations across different charge transitions was recently observed in a double quantum dot interferometer experiment⁴⁷. In Section 6 of the Supplementary Information, we discuss oscillations with different periods that are observed at other points in the parameter space of the device.

We support this interpretation by reproducing our results with quantum dynamics simulations that incorporate rf drive power, charge noise and temperature. To build intuition for those simulations, we use an idealized model (see Section 2.2 of the Supplementary Information) subject to the following assumptions (which we will later relax): the wire is in the topological phase and there are no sub-gap states other than the MZMs; the charging energy and level spacing in the dots are much greater than the temperature; dots 1 and 3 are sufficiently detuned that their influence is fully encapsulated in the effective couplings t_L and t_R to MZMs at the ends of the wire (see Fig. 1a); and the drive frequency and power are both negligible. In this limit, the quantum capacitance as a function of the total fermion parity in the quantum dot–wire system, Z, is given by

in which E_D is the detuning from the charge-degeneracy point, α is the lever arm of the plunger gate to the dot, E_M is the MZM energy splitting and T is the temperature. The net effective tunnelling that results from the interference between different trajectories from the dot to the MZMs and back, t_C(Z, ϕ), is

Here ϕ is the phase difference between t_L and t_R, which is controlled by the magnetic flux Φ through the interference loop created by the dot, the wire and the tunnelling paths between them according to ϕ = 2πΦ/Φ₀ + ϕ₀, in which Φ₀ = h/e and ϕ₀ is a flux-independent offset. To capture the extent to which C_Q can be used to discriminate between Z = ±1, it is convenient to introduce

The interferometer must be well balanced t_L ≈ t_R for ΔC_Q to be large according to equation (1). When E_M = 0, ΔC_Q exhibits maxima along the E_D = 0 line, with flux periodicity h/2e.

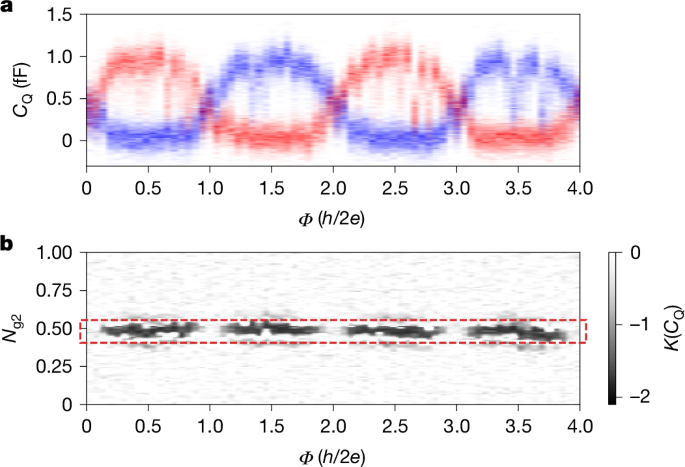
For detailed comparison with experiments, we use the methods discussed in Sections 2.4 and 2.5 of the Supplementary Information to simulate a more complete model of the device and readout chain that includes the full triple-dot system, incoherent coupling to the environment (using parameters inferred from separate measurements; see Sections 9 and 10 of the Supplementary Information) and measurement backaction. Crucially, this approach allows us to incorporate different noise sources in a systematic and quantitative way without any free parameters. The simulated dynamical C_Q, defined in Section 2.3 of the Supplementary Information, is shown in Fig. 4. The C_Q histograms in Fig. 4a reveal two h/e-periodic branches (one shown in red and the other in blue), associated with the two parities of the coupled system. If the fermion parity Z were perfectly conserved, then the device would remain in one of the two parity eigenstates and the Φ dependence would follow either the blue or the red trace in Fig. 4a. However, Z should fluctuate on a timescale given by the quasiparticle poisoning time τ_qpp. Hence, in traces over times longer than τ_qpp, a bimodal distribution of C_Q values is expected, that is, both the blue and red traces in Fig. 4a. Consequently, the kurtosis K(C_Q) exhibits minima at which ΔC_Q is peaked, as shown in Fig. 4b, and time traces taken at these points will exhibit a telegraph signal composed of switches between the values C_Q(1, ϕ) and C_Q(−1, ϕ). Comparing Fig. 4 with Fig. 3h,i, we find good overall agreement of both the histograms and the kurtosis. We find a maximum ΔC_Q(Φ) ≈ 1 fF, which is consistent with our measurements in Fig. 3. This agreement extends to other parameter regimes, such as when the interferometer is poorly balanced or the splitting E_M is sizeable, as discussed in Section 6 of the Supplementary Information.

Simulated dynamical C_Q as a function of magnetic flux and dot 2 gate offset charge N_g2, including the effects of charge and readout noise, as well as non-zero temperature, drive power and frequency, per the discussion in the text. a, Histogram of the two parity sectors for fixed N_g2 = 0.49. Here we used t_m1 = t_m2 = 6 μeV, t₁₂ = t₂₃ = 8 μeV, E_C1 = 140 μeV, E_C2 = 45 μeV, E_C3 = 100 μeV, N_g1 = N_g3 = 0.3, T = 50 mK and E_M = 0. b, Kurtosis of C_Q(t) as a function of N_g2 and flux through the loop. The middle of the dashed red rectangle indicates the N_g2 value used for the linecut in panel a.

A second measurement of device A and a measurement of a second device (device B) give results in qualitative agreement with those of measurement A1, demonstrating the reproducibility of the observed phenomena (Section 5 of the Supplementary Information). We have tested our interpretation by: (1) disconnecting the dots from the wire; (2) measuring at fields of 0.8 T below the region identified by TGP; (3) intentionally injecting quasiparticles into the superconductor and observing the effect on τ_RTS; and (4) comparing the quasiparticle density measured in a separate test structure with that inferred according to the hypothesis that τ_qpp = τ_RTS ≈ 2 ms (Section 7 of the Supplementary Information).

By extending the model introduced above, we have analysed the quasi-MZM scenario discussed in previous works^37,38,39,48. We introduce an extra pair of ‘hidden’ Majorana modes that are weakly coupled to each other and to the visible MZMs, which themselves are coupled to quantum dots 1 and 3. Together, the hidden and visible MZMs form a trivial low-energy state at each end of the wire. This scenario can occur in the trivial phase, in which it requires some fine-tuning to make the couplings small. In Section 2.7 of the Supplementary Information, we show that the hidden Majorana modes suppress ΔC_Q owing to fast fermion tunnelling between them and the visible MZMs. This effect completely washes out the flux-dependent bimodality unless the coupling between the ‘hidden’ Majorana modes and the visible MZMs is less than 1 neV or the hidden Majorana modes are effectively gapped out, as shown in Supplementary Fig. 4.