Impacts of climate change on global agriculture accounting for adaptation

This section provides an overview of the data and methods used to estimate the relation between agricultural yields and variation in weather, accounting for adaptation to climate and economic development.

Agricultural data

Subnational yields, production and harvested area, primarily at the second administrative level, were collected from the statistical offices of 54 countries (Supplementary Fig. 1 and Supplementary Table 1). This includes data that were generously shared for Burma, Cambodia, Laos, Malaysia, Thailand⁵² and Zambia⁵³. This yields a dataset for 6 crops in 12,658 locations (41,186 location–crop pairs) spanning up to 137 years. Wheat varietals, when not identified in the data, were manually assigned to spring or winter wheat based on ancillary country-specific data (Supplementary Table 6). All growing season definitions are from ref. ⁵⁴ and held fixed. Detailed information is provided in Supplementary Information, section A.

Historical weather data

The main weather dataset used in this analysis is the Global Meteorological Forcing Dataset (GMFD v1)⁵⁵. Data are available on a 0.25° × 0.25°-resolution grid from 1948 to 2010. We obtain daily maximum and minimum temperatures and daily total precipitation for all grid cells globally. These data provide surface temperature and precipitation information using a combination of observations and reanalysis, which is downscaled and bias-corrected using several station-based observational datasets to remove biases in monthly temperature and precipitation.

Projected weather data

We use the NASA Earth Exchange (NEX) Global Daily Downscaled Projections (GDDP) dataset for future projections of climate change. This comprises 21 climate projections, which are downscaled to 0.25° × 0.25° resolution⁵⁶ from global climate model (GCM) runs in the Coupled Model Intercomparison Project Phase 5 (CMIP5) archive⁵⁷. NEX-GDDP uses GMFD⁵⁵ and quantile mapping to adjust the GCM outputs (means and variances) in historical and future time periods so that the systemic bias of the GCMs is removed. In contrast to other approaches⁵⁸, NEX-GDDP does not assume a common distribution shape between observed (GMFD) and GCM data. However, NEX-GDDP only assumes that GMFD (versus GCM) variances are correct, which other approaches⁵⁸ do not require. Climate is projected under emissions from Representative Concentration Pathways 4.5 and 8.5 (RCP 4.5 and RCP 8.5) up to 2100 (refs. ^59,60), although the NEX-GDDP outputs of some models lack precipitation data past 2098, so that the ‘end of the century’ in this paper is the year 2098. The CMIP5 ensemble of GCMs is not a systematic sample of possible futures. To provide an ensemble of climate projections with a probability distribution of GMSTs consistent with that estimated by a probabilistic simple climate model, we use the method outlined in ref. ⁶¹ to assign probabilistic weights to climate projections. A full list of models and their weights is given in Supplementary Table 9. For a more complete description, see ref. ²⁹.

Historical income data

We obtain national and subnational income data for 1,503 administrative regions from 83 countries from ref. ⁶². Data are provided by ref. ⁶² at the state/province level for each country. We use these subnational data to allocate national GDP data from the Penn World Tables (PWT) database (https://www.rug.nl/ggdc/productivity/pwt/) under the assumption that the within-country distributions of GDP recorded in ref. ⁶² are accurate, but the exact levels may not be. Using these data, we construct a consistent panel of subnational incomes for all areas in our crop dataset that sum to the national GDP from the PWT database for all countries in the sample.

Projected income data

Future projections of national incomes are derived from the Organization for Economic Co-operation and Development (OECD) ENV-Growth model⁶³ and the International Institute for Applied Systems Analysis (IIASA) GDP model⁶⁴, as part of the ‘socioeconomic conditions’ of the Shared Socioeconomic Pathways (SSPs)⁶⁵. These are the only models that provide GDP per capita projections for a wide range of countries in the SSP database. The SSPs propose a set of plausible scenarios of socioeconomic development over the twenty-first century in the absence of climate impacts and policy. Data are interpolated to annual frequency and downscaled following ref. ²⁹.

Irrigation data

We obtain data on the area equipped for irrigation from AQUASTAT of the Food and Agriculture Organization of the United Nations (FAO)⁶⁶. These data are a single cross-section centred around the year 2000 at 0.08° × 0.08° resolution and we hold the values fixed in climate projections. (Increases in incomes and heat exposure may drive increases in future irrigation, whereas aquifer and reservoir drawdown may drive decreases in future irrigation).

Model overview

We develop a reduced-form approach to modelling crop yields and producer adaptation, allowing us to recover plausibly causal effects of weather on yields based on data from real-world farms, without having to observe all of the biophysical processes in a given crop that mediate these effects. The approach allows us to account for the total costs and benefits of numerous real-world adaptive adjustments that producers undertake, without requiring that we observe or model each adjustment explicitly. This approach builds on ideas and techniques developed in refs. ^4,19,26,27, using the method for capturing the benefits of adaptation in ref. ²⁸ and accounting for its costs based on the revealed preference approach in ref. ²⁹. Following common practice in the literature², our implementation also allows our model to recover local, micro level and instantaneous nonlinear effects of environmental conditions, even though outcome data are only observed at more aggregate spatial scales and temporal frequencies^28,31.

We apply cross-validation techniques common in machine learning but adapted for model selection in a causal inference context. Our approach has three stages: (1) we remove variation that is associated with non-parametric controls to condition out the influence of unobservables; (2) we apply cross-validation to this residualized data to select weather measures; and (3) we again apply cross-validation, modifying the model chosen in the previous step to select dimensions of climate that matter for adaptation. We perform the sequence (1)–(3) for each of the six crops separately to identify the most suitable model for each crop. Having selected and fitted an empirical model that accounts for weather and adaptation, we then apply the model in projections of climate change impacts. Each of these steps is detailed below.

Construction of weather terms

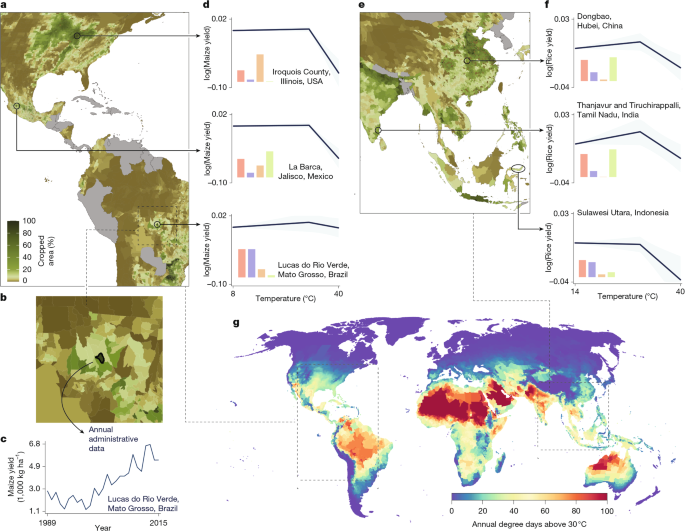
A large number of candidate weather variables are constructed from raw weather data based on previous literature^{5,67,68,69,70,71}. We assemble variables that previous analyses report were influential for at least one crop, although individual variables might not ultimately be included in the specification for all or any crops. All weather transformations were conducted at the pixel level using daily data before aggregation, unless otherwise specified. Encoding pixel-by-day weather data after nonlinear transformations allows a high degree of flexibility in how local daily weather conditions can have an instantaneous and nonlinear impact on crops^28,31. This means that even short periods of environmental stress are resolved and captured by these variables and the model. Degree day terms were constructed following ref. ⁵, with kink points selected for each crop by a tenfold cross-validation search over potential kinks. Growing-season-phase precipitation was summed within month by grid cell and then transformed⁷⁰. Construction of vapour pressure deficit followed ref. ⁶⁹. The count of rain days was calculated by grid cell as days with positive precipitation⁶⁸. Extreme rain was identified by constructing the 1980–2010 rainfall distribution for each grid cell in the GMFD daily precipitation data and aggregating the amount of rainfall or number of days of rainfall in excess of the 95th percentile of this distribution⁶⁸. Count of extreme rain days was measured following extreme rain except grid cell days were counted instead of summed within grid cell⁶⁸. Drought was defined as a binary indicator over administrative unit growing season precipitation, using a tenfold cross-validation search over percentile cut-offs in the administrative unit growing season total precipitation distribution, largely following ref. ⁷¹ (final cut-offs ranged from the 8th to 25th percentiles). Minimum temperatures were calculated as the average of daily grid cell minimum temperatures within each month, following ref. ⁶⁷. For all weather terms, weighting and aggregation to administrative units were done as described in ref. ²⁹ with cropped area weights from ref. ⁵⁴. See Supplementary Information, section D and Supplementary Tables 2–5 for full details on the construction of each weather variable.

Cross-validation step zero: residualizing data for causal inference

We first select non-parametric controls for unobservable factors to isolate plausibly random variation in our set of weather measures^5,22,31. Specifically, we use administrative unit i (typically county), fixed effects \({\mu }_{i}\), absorbing time-invariant confounds such as soil quality; country–year fixed effects \({\rho }_{ct}\), absorbing country-by-year price and trade policy confounds; and state or province quadratic time trends \({h}_{s}(t)\), absorbing slow-moving, local confounds such as the diffusion of new technologies or local variation in prices (equation (1), Supplementary equations (B.12) and (D.1)–(D.6)). We separately partial out the variation in yields y_it and the vector of regressors x_it on these non-parametric controls (Supplementary Information, section B), leaving us with residual variation \({\widetilde{y}}_{it}\) and \({\widetilde{{\bf{x}}}}_{it}\) for our cross-validation procedures.

Cross-validation step one: selection of weather measures

We implement cross-validation over ten random folds to systematically evaluate the importance for yields of the broad range of weather measures previously described in the literature. Each potential model is required to have at least one temperature term and one moisture term. (Temperature and precipitation are known to be correlated, so causal effects estimation of one without controlling for the other is vulnerable to bias⁵. Vapour pressure deficit was treated as a moisture term. Note: these terms may affect moisture demand and/or soil moisture supply). Weather terms are each interacted with a fixed set of covariates: growing season average daily maximum temperature (‘long-run temperature’, \(\overline{T}\)), growing season average monthly precipitation (‘long-run precipitation’, \(\bar{P}\)), log(GDP_pc) (‘income’, \(\bar{I}\)) and the share of cropped area equipped for irrigation (‘irrigation’, \(R\)). This ensures that weather variable selection occurs using models that are at least as flexible as those selected after the second cross-validation step, without having to simultaneously explore the full set of potential combinations of weather measures and covariate interactions (which would number 103,904 separate models). In selecting a candidate set of weather terms over which to study adaptation, we seek to optimize over parsimony and explanatory power, selecting a high-performing model in which additional weather terms do not individually contribute substantial fit gains (see Supplementary Tables 7 and 8).

Not all weather terms can be reliably projected by climate models^72,73,74 and models containing these candidate variables were explored in the cross-validation procedure (Extended Data Fig. 2) but ultimately excluded in projections of climate change because they could not be projected with reasonably high confidence. Overall, this procedure evaluates the out-of-sample (OOS) performance of candidate models that include all combinations of weather variables that we draw from the literature and allows for varying degrees of nonlinearity (Fig. 1, Extended Data Figs. 1a and 2 and Supplementary Information, sections B–D).

Cross-validation step two: selection of variables that capture adaptation

In our second cross-validation step, we select a set of covariate interactions for which covariates reflect the factors that mediate producer adaptation actions^{4,19,26,27,75,76} (equation (B.7)). We take as given the set of weather parameters selected from the first step, allowing for interactions between weather variables and income, irrigation, \(\bar{T}\), \(\bar{P}\) and/or \(\bar{T}\times \bar{P}\). Further, we allow for the nonlinear precipitation response to vary over phases of the growing season or to be constant over the growing season, with ‘phases’ of the growing season defined by a systematic model search (Supplementary Table 4). Finally, we also allow for interaction terms between degree day responses and monthly precipitation.

Accounting for mediating effects of income and irrigation is important because access to resources alters producer actions through several channels—such as access to technology^{77,78,79,80,81}, insurance and credit markets^77,80,82,83, inputs such as fertilizer^77,84 or labour markets^77,79,81 or information⁸⁵. Notably, this minimizes confounding in our estimates, as resources and climate tend to be correlated (for example, poorer nations tend to be located in the tropics⁸⁶) and it allows our model to capture that climate and income jointly determine yields⁸⁷. Further, this allows us to project future changes associated with economic development.

In this step, we use cross-validation with ten folds over random blocks of data grouped by state/province. Here the test of model performance is the ability to model yields for a set of states or provinces that are held out of the data. This matches one of the intended uses of our interaction surface, which is to model the heterogeneous response of yields to weather for locations with no yield data available.

In our climate projections, long-run average precipitation (\(\bar{P}\)) values range more than 17 standard deviations outside the mean in our historical data. To prevent extrapolating adaptation behaviour to \(\bar{P}\) values far outside our data, we imposed a single-knot linear spline in \(\bar{P}\) for each weather measure (\({z}_{a}(\bar{{P}_{i}})\), \({z}_{b}(\bar{{P}_{i}})\) and \({z}_{c}(\bar{{P}_{i}})\) below). These knots were chosen using a within-R² search over knot locations (Supplementary Information, section D). See Supplementary Information, sections B–D for further estimation details.

Example specification for maize

The final maize specification is:

with

in which y_it is log(yields) in administrative unit i in year t, \({{\rm{DD}}}_{it}^{8-31}\) represents degree days from 8 °C to 31 °C, which is interacted with each of average growing season daily maximum temperature (\({\bar{T}}_{i}\)), splines in average growing season total precipitation (\({z}_{[\cdot ]}({\bar{P}}_{i})\)), the interaction between \({\bar{T}}_{i}\) and \({z}_{[\cdot ]}({\bar{P}}_{i})\), average log(GDP_pc) (I_i) and area equipped for irrigation (R_i). The remaining weather terms have similar interactions. prcp_phase[j]_it represents monthly precipitation summed within growing-season-phase j, for j ∈ {1, 2, 3}. μ_i, h_s(t) and ρ_ct are as described previously. Standard errors of all estimated parameters allow for the correlated nature of yields (and weather) across space and over time. Specifically, we estimate cluster-robust standard errors⁸⁸, which allow arbitrary correlations across observations over time within first-level administrative units (that is, autocorrelations within and between counties within a given state) and across all observations within a given country–year. See ref. ³¹ for a discussion of this issue in this context. Note that the terms in equation (1) reflect rows (weather variables) and columns (mediating variables) illustrated in Extended Data Fig. 1b. See Supplementary Information, section D, for full details of the final model specification for each crop.

We note that the overall fit of the above empirical model to the historical data is high, with an R² of 0.85 for maize. For reference, the seminal analysis of maize by Schlenker and Roberts⁵ report a model R² of 0.77 when modelling yields for only the Eastern United States, for which data quality is high relative to much of the globe and the underlying patterns of producer behaviour are probably more homogeneous across locations.

Accounting for adaptation costs

We are able to empirically observe the benefits of adaptive management among producing regions because adaptation decisions have costs^19,26. If adaptations were free, then we would expect all regions to use uniform management practices and varieties using only the most climate-resilient technology available, as this strategy would convey benefits at no cost^19,29. To capture the full impact of climate change on agricultural systems, it is therefore essential that these costs of adaptation are accounted for, as well as adaptation benefits, as these costs would not be incurred in the absence of climate change.

We cannot observe these costs directly but they can be inferred under the assumption that profit-maximizing producers undertake adaptations for which the benefits exceed costs, but not those for which costs exceed benefits²⁹. This is referred to as a ‘revealed preference’ approach and is widely used in economics research⁸⁹. Specifically, we follow the approach developed in ref. ²⁹ to track these costs for each crop and in each region until 2100 (see Supplementary Information, section H, for a derivation, Supplementary Fig. 6 for intuition and Supplementry equations (H.6) and (H.7) for a detailed example). We follow ref. ¹⁹ and deduct these costs from yield changes to develop a complete measure of climate change impacts²⁹. Thus, our projections of climate change impacts on yields should be interpreted as capturing both the costs and the benefits of voluntary producer adaptations in each location.

Intuitively, consider the term \({\gamma }_{6}{\bar{T}}_{i}\) in equation (1), through which long-run average temperature in region i (\({\bar{T}}_{i}\)) modulates the negative effect of extreme heat shocks (\({{\rm{DD}}}_{it}^{31+}\)) on yields. A 1 °C increase in \({\bar{T}}_{i}\) flattens the negative extreme heat slope by γ₆ log points per extreme heat degree day—a benefit of adaptation in hotter climates. If a producer in this example expects ten extreme heat degree days during the growing season, then the expected adaptation benefit for a 1 °C increase in \({\bar{T}}_{i}\) would be 10 × γ₆ log points of yields. This benefit must not be costless, otherwise producers would have already adapted away all extreme heat yield losses. We thus infer marginal adaptation costs as equal to the marginal adaptation benefits that we estimate (an implication of assuming that producers maximize profits; see Supplementary Information, section H for details).

Model estimates

Weather variables that influence crop yields

Many correlated aspects of weather affecting crop biophysical processes have been separately studied^{2,5,36,67,68,69,70,71,101,102,103} and we evaluate which are important drivers of the biophysical processes affecting yields of each crop. We use cross-validation to evaluate more than 8,000 candidate empirical models across all six crops, for which each model predicts residual changes in historical crop yields using a different combination of weather variables proposed by previous studies^{5,67,68,69,70,71}. On the basis of OOS performance, we find that nonlinear degree days are the most important determinant of yields, on average across crops, by a considerable margin (Extended Data Figs. 1a and 2). Degree days increases model OOS fit (Supplementary Table 7) across crops by 51.7% on average (relative to the second-best model), with the largest gain for sorghum (101.6%, a doubling of model OOS fit) and the smallest gains for rice and cassava (9.1% and 9.4%). In general, exposure to cool daily temperatures (<9 °C for wheat and <29–31 °C for all other crops) modestly increase yields, whereas daily temperatures above these thresholds cause sharp declines in yields; for example, lowering end-of-season maize yields by −5% for each day that shifts from a 25 °C to a 40 °C day (Fig. 1g and Extended Data Fig. 3). This finding generalizes previous results from the USA (for example, see ref. ⁵) globally and across crops.

Seasonal precipitation is the second most important determinant of yields across all crops, to the exclusion of a wide range of other candidate weather variables put forward in the literature (Extended Data Figs. 1a and 2). Nonlinear measures of seasonal precipitation increase model OOS fit across crops by 14.5%, with the largest gains for rice and maize (22.8% and 22.2%) and the smallest gains for wheat, soybean and sorghum (7.8%, 9.2% and 9.4%; Supplementary Table 8). Across crops, increasing seasonal monthly precipitation raises yields on average 0.2% per mm at low rainfall levels (<100 mm per month), has little effect at intermediate levels (250–300 mm per month) and reduces yields −0.6% per mm at higher levels (>400 mm per month; Extended Data Figs. 3 and 4).

In contrast to reports from individual empirical studies (for example, refs. ^67,68,69,71), we find that monthly average minimum temperatures (t_min), vapour pressure deficit, drought, the count of rain days, the count of extreme rain days and the amount of extreme rain generally only contribute modest gains to yield model fits (average % gains in OOS fit range from 1.2% to 3.6% excluding drought for cassava, discussed below). Minimum temperatures are important predictors for rice and wheat yields but not other crops (Extended Data Fig. 2 and Supplementary Tables 7 and 8).

There are exceptions for individual crops. Cassava yields are generally insensitive to weather overall (the maximum OOS variance predicted is 2.3%), motivating its cultivation in contexts in which the climate is not conducive to other staple crops that are more sensitive¹⁰⁴. We find that growing season drought is the most important factor for predicting cassava yields (24.0% gain in variance predicted; Supplementary Table 7). Drought is also important for rice yields, as is the count of rain days (6.4% and 8.0% gain in variance predicted; Supplementary Table 7). The count of rain days is also moderately important for maize yields (6.6% gain in variance predicted; Supplementary Table 7). Taken together, these results indicate the importance of nuanced projections of future precipitation distributions for a restricted set of global staple crops.

Adaptation to climate

We find that producers adapt to higher temperatures such that, across crops and around the world, yields are systematically less sensitive to daily temperature and generally more sensitive to seasonal precipitation in locations that are hotter on average (Fig. 1 and Extended Data Figs. 1b, 3a,e and 4a,e). Similarly, yields are less responsive to temperature and more responsive to precipitation in locations that are drier on average (Extended Data Figs. 1b, 3b,f and 4b,f). Because climate-associated adaptations influence numerous—possibly correlated—aspects of weather–crop responses, we estimate the mediating influence of all dimensions of climate simultaneously on all dimensions of weather for each crop, generating a multidimensional function describing these interacting relationships (Extended Data Figs. 3 and 4). This function serves as the basis for projecting adaptation to climate change (Methods and Supplementary Figs. 4 and 5) and has not been previously represented in global process-based models^7,8.

Economic development

We also find that rising incomes enable producers to respond to environmental conditions in important but varied ways, thereby mediating the effects of different climates. For example, maize and sorghum yields become more sensitive to temperature as incomes rise, whereas rice and cassava become less sensitive (Extended Data Figs. 1b and 3c). These differences could be because of differences in how access to improved technologies, infrastructure, banking and credit or insurance^77,78,80,82 influence producer strategies^77,83. Notably, however, we find that higher incomes and access to irrigation are associated with greater resilience to precipitation extremes across all crops (Extended Data Figs. 1b, 3g and 4g), consistent with access to improved irrigation technologies increasing with income^77,80.

Projections and the partial SCC

We integrate our econometric results with the DSCIM^28,29 to develop projections and partial SCC estimates (Supplementary Information, section K.5). Calculations were conducted as described in refs. ^28,29, over 24,378 geographically granular regions, 33 climate models and 1,920 Monte Carlo draws of statistical uncertainty per crop. Following ref. ²⁹, we project the impacts of climate change net of adaptation and its costs, relative to a counterfactual in which incomes grow but the climate is held fixed. Projections in percentage terms represent weighted averages of log yield estimates, converted to percentages. Crop impacts are aggregated over space using cropped area weights (Supplementary Information, section A), over climate models using surrogate model mixed ensemble⁶¹ weights (Supplementary Table 9) and over crops using calorie weights⁹⁰. Yield gains from CO₂ fertilization are difficult to empirically quantify^91,92,93,94 but we adjust our projections to incorporate CO₂ fertilization using previous estimates⁹. Yield projections are robust to restricting future weather projections to be bound within the support of the historical data (Supplementary Table 12 and Supplementary Fig. 12). See Supplementary Information, section G for full details of the projection methodology.

To calculate a partial SCC, we must value climate-induced changes in yields for both producers and consumers (Supplementary Figs. 19 and 21). Our approach to this valuation follows ref. ⁹⁵ and models consumers and producers of calories with constant elasticity of demand and supply, drawing elasticities from the literature^95,96,97. We allow for frictionless crop trade within country but do not allow for trade between countries. We test sensitivity to this assumption by allowing frictionless trade between countries within continents and throughout the globe. We consider the potential impacts of crop switching, shifting of cropped areas and international trade by drawing on the previous model-based literature^75,98,99,100. In calculating the SCC, we follow ref. ²⁸ to calculate results for constant discount rates (2%, 2.5%, 3%, 5%) and refs. ^28,47 for Ramsey discounting (ρ = 0, η = 2). See Supplementary Information, section K, for full details of the valuation methodology.

Methodological challenges

A challenge to this analysis is the limited way in which future resource access has been projected¹⁰⁵, that is, relying on standardized scenarios contained in the SSPs⁶⁵. Numerous types of resources probably influence how staple crops are managed. However, we restricted our analysis to consider only the mediating effects of income and irrigation. We treat income as a proxy measure for access to resources associated with economic development, such as fertilizer or extension services. These variables are intentionally omitted from regression models so that their influence will be captured by the income variable, allowing them to be represented in standard socioeconomic projections for which income is projected and available to us, but these other variables are not⁶⁵. Mediating effects of irrigation are accounted for explicitly because they are influential and irrigation presence is dependent on groundwater geology, local topography and surface water flows, which are not well captured by income nor climate measures. An important area for future work is to develop projections of irrigation for use in crop yield projections.

Another challenge is that our measures of climate used to estimate adaptation are cross-sectional; thus, correlations between climate and omitted variables that determine the shape of the yield–weather response could potentially bias our estimates of adaptation. If such correlations exist, they might be regional in nature or otherwise only affect limited subsamples of our data. As a partial test of this possibility, we examine non-parametric estimates of the association between climate and temperature sensitivity and find that the associations we rely on are systematic throughout the data (Supplementary Fig. 3). This suggests that any unknown omitted variable would have to be consistently correlated with climate throughout our sample to influence our analysis.

We are able to account for some, but not all, potential shifts in crop growing seasons under future climate change. Our parameterization of adaptation implicitly captures effects of shifting the harvest date earlier in the growing season (for example, to avoid late-season heat exposure; see Supplementary Information, section B). However, we cannot capture the effects of planting dates that may shift to a period before the start of our growing season windows nor can we capture crop switching in our yield models (although we do capture it in the valuation of impacts; see Supplementary Information, section K). We note that such shifts may not depend only on temperatures but also on rainfall quantity and timing, which are not yet well modelled by existing GCMs^72,73,74. These are forms of adaptation that some process-based models explicitly include^{7,8,9,18,106,107,108}. Furthermore, unlike process-based models, our reduced-form approach by design does not capture the agronomic mechanisms by which climatic changes influence future yields. Such mechanistic insights can be used to guide crop research in expectation of future climate stresses^41,42,43,44, highlighting an important trade-off in the two methodological approaches (Supplementary Information, section B.1).

For precipitation effects, we do not project some extreme precipitation effects because these precipitation extremes are not well captured by the existing suite of GCMs^72,73,74. We highlight this as an area of need for future research from the climate modelling community, with potentially important implications for our further understanding of climate change impacts to global food security.

Also, we note that our valuation of agricultural damages from climate change and the partial SCC only accounts for the crops in our sample, which account for a large share of global calories but a smaller share of total agricultural revenues. The present analysis does not include effects of climate change on other sources of agricultural revenue, such as livestock, citruses and other specialty crops. We look to future work to incorporate these output categories.