Immigrant–native pay gap driven by lack of access to high-paying jobs

Data and measures

Linked employer–employee administrative records and meta-analytic data

We used recent linked employer–employee administrative records (administrative records that link individual employees directly to their employers and coworkers) from nine countries in Europe and North America (Canada, Denmark, France, Germany, the Netherlands, Norway, Spain, Sweden and the USA). These linked employer–employee administrative records can be used for approved research purposes by individuals with the proper authorizations from the relevant national statistical agencies. We use these administrative records to create a dataset that contains immigrant–native pay differences net of human capital within the same job, occupation, establishment, industry, and in the labour market as a whole. We subsequently analyse these differences using a random effects meta-regression model and report the results of this meta-analysis in our paper. When meta-analysis is conducted on results from the same model across different samples (as is the case here), it is in principle equivalent to running one model for all countries.

Key features and reliability of administrative records

A summary of the key features of the administrative records across countries is provided in Extended Data Table 1. Below, we provide a general description of the measurement of key variables used in the analysis. The administrative records used in our analysis are of high quality, enabling detailed comparisons of workers within the same occupation and employer. However, harmonizing administrative records across countries presents inherent challenges due to variation in sources, definitions, and variable measurements. Extended Data Table 1 highlights cross-national differences in sample size, information sources and key variables such as immigrant background, industry, occupation, employer and job (defined as unique combinations of occupation and employer identifiers) across our nine countries. Given the unique nature of each country’s administrative records infrastructure, we include additional details in the Supplementary Information (Section 6), covering variable measurement, relevant country-specific supplementary analyses and a brief overview of the immigration context in each country.

To address potential biases related to cross-national comparability and the reliability of our findings, we conducted extensive sensitivity analyses, summarized in Extended Data Figs. 6–8 and described in detail in Supplementary Information, section 4 and Supplementary Tables 25–39. These analyses assess the robustness of our results to different methodological choices, including alternative measures of pay (annual earnings versus hourly wages; Extended Data Fig. 6 and Supplementary Table 25–27), varying levels of occupational granularity (four-digit codes versus coarser classifications; Extended Data Fig. 7 and Supplementary Tables 29–31), different methods of identifying employers (establishment-level versus firm-level identifiers; Extended Data Fig. 7 and Supplementary Table 32), the exclusion of control variables (education, geographic region, age; Extended Data Fig. 8 and Supplementary Tables 33–36), varying the age restrictions defining the sample; Extended Data Fig. 8 and Supplementary Table 37, and the inclusion of additional control variables (seniority, part-time/full-time employment; Extended Data Fig. 8 and Supplementary Tables 38–39).

Each sensitivity analysis is discussed below in relation to the specific measurement issue it addresses, with comprehensive descriptions provided in Supplementary Information, section 4. Collectively, these analyses confirm the robustness of our findings to variations in variable definitions, measurement approaches, and modelling specifications.

Earnings and wages

We use the natural logarithm of annual earnings as our dependent variable. The measure of annual earnings is based on pre-tax earnings and is a function of hourly wages, annual hours worked and additional compensation such as overtime pay, performance bonuses and other wage components contributing to take home pay. For the countries where we can isolate hourly wage on contractual hours (Denmark, the Netherlands and Norway) or hourly earnings (France, Spain and the USA), we report estimates using these alternative wage and earnings measures to capture compensation per hour worked (Supplementary Tables 25–27).

Immigrant background

In five countries (Canada, Denmark, the Netherlands, Norway and Sweden), we can identify the country of birth of individuals and their parents. Immigrants are defined as persons who were born abroad, while children of immigrants are defined as persons who were born in their current country of residence to two foreign-born parents; both groups are compared to natives, defined as individuals who were born in their country of residence to native-born parents. In three countries (France, Spain and the USA), only an individual’s country of birth is available (that is, information on their parents’ country of birth is not available), allowing us to compare immigrants (those born abroad) to natives (in this case, those born in their country of residence). For Germany, information on the country of birth is unavailable, and so we identify immigrants and children of immigrants using longitudinal data on citizenship status, nationality and name-based information derived from social security records (details provided in Supplementary Information, section 6.4.2).

World region of origin

For analyses examining differences by world region of origin, immigrants and children of immigrants are grouped into five broad world regions: Asia; Europe, North America, and other Western countries; Latin America; Middle East and North Africa; and Sub-Saharan Africa (Supplementary Table 1 provides a detailed list of countries within each region). For Canada, Denmark, France, the Netherlands, Norway, Spain, Sweden and the USA, region of origin is determined by country of birth for immigrants and parental country of birth for children of immigrants, prioritizing the mother’s country of birth when immigrant parents differ. Information on country of birth is unavailable in Germany, so we use information on nationality upon labour market entry for immigrants and information on first names for children of immigrants to provide a precise categorization for region of origin (details provided in Supplementary Information, section 6.4.2).

Duration of stay

Supplementary analyses (Extended Data Fig. 1 and Supplementary Tables 10–12) report results for immigrants disaggregated by duration of stay in seven countries (Canada, Denmark, France, Germany, Norway, Sweden and the USA). Immigrants are categorized as: recent immigrants (less than 10 years since arrival); established immigrants (10 or more years since arrival); and childhood immigrants (individuals who immigrated at 17 years old or younger).

Industry

Industry refers to the primary economic activity of the esstablishment where an individual is employed, defined by the type of goods and services it produces. For Denmark, France, the Netherlands and Norway, industry is classified using the four-digit nomenclature of the Statistical Classification of Economic Activities in the European Community (NACE), while Germany and Sweden are classified using three-digit NACE codes. For Spain, we rely on two-digit codes from the National Classification of Economic Activities (CNAE). For Canada and the USA, industry is classified using three-digit codes from the North American Industrial Classification (NAICS).

Establishment

Employers are identified using unique establishment identifiers in Denmark, France, Germany, the Netherlands, Norway, Spain and Sweden. Establishments typically refer to distinct workplaces, often defined by a unique postal address, and are distinct from firms except in cases of single-establishment firms. In Canada and the USA, employers are identified using unique firm-level identifiers, which can encompass multiple establishments across geographic locations. For countries with information on both establishments and firms (Denmark, France, the Netherlands, Norway, Spain and Sweden), we report additional results using firm identifiers to assess the robustness of our findings to this alternative employer measure (Supplementary Table 32).

Occupation

We use four-digit codes from national adaptations of the International Standard Classification of Occupations (ISCO) to measure occupations for Denmark, Germany, Norway and Sweden. In Canada, the three-digit Canadian National Occupational Classification system (NOC) is used, while in the USA, occupations are measured using three-digit categories from the Standard Occupation Classification (SOC) system. For the Netherlands, we use ISCO codes measured at the two-digit level due to small sample sizes at the job level (occupation–establishment level). In France, where job-level sample sizes are also small, we use two-digit occupation codes from a coarsened version of Nomenclature des Professions et Categories Socio-Professionelles (CSP) with 30 occupational categories. For Spain, occupation is classified using the employer-reported one-digit grupo de cotización (10 categories) system. To evaluate the impact of occupational granularity for our results, we provide sensitivity analyses coarsening occupational measures to one-, two- and three-digit levels for countries with detailed occupational information (Supplementary Tables 29–31).

Occupation–establishment units

Jobs are defined as the intersection of occupation and establishment (or firms), with the occupation–establishment units representing unique job cells⁵⁸. Within-job pay gaps refer to the estimated pay differences within these occupation–establishment units. This conceptualization of jobs aligns with the understanding of jobs as settings where individuals are hired to do specific tasks—often within the same work group—in the same workplace or company. However, highly detailed occupational and job titles may just reflect wage level indicators instead of distinguishing the actual content of work performed⁵⁸. To address this, we provide results using coarsened definitions of jobs based on one-, two- and three-digit occupational codes when defining occupation–establishment units (Supplementary Tables 29–31). For countries with information on both firms and establishments, we also report results where jobs are defined as occupation–firm units (Supplementary Table 32). We also report results where we restrict the sample in all models to only include individuals working in immigrant–native integrated job cells (that is, excluding workers in jobs occupied only by natives or only by immigrants and their children; Supplementary Table 28).

Covariates

Our main analyses adjust for sex, educational attainment, geographic region, and age. Sex is coded as a binary variable distinguishing men and women (Extended Data Figs. 2 and 3 and Supplementary Tables 13–18 present results from separate analyses for men and women). Educational attainment is categorized into four or five levels: less than upper-secondary education; completed upper-secondary education; short tertiary education (for example, Bachelor’s degrees or equivalent); long tertiary education (for example, Master’s degrees or equivalent); and, where available, doctoral degrees (see Extended Data Figs. 4 and 5 and Supplementary Tables 19–24 for results from separate analyses for highly educated workers and workers with less education). A separate indicator is included for individuals with missing educational information. Geographic region is captured using a set of dummy variables for local labour markets (for example, municipalities or counties; see country-specific descriptions in Supplementary Information, section 6). Age is modelled using both linear and quadratic terms.

Sample restrictions

We use the most recent information available to us, which ranges from 2016 to 2019, depending on the country. We restrict our main samples to workers between ages 25 and 60. For each worker, we select the job observation with the highest annual earnings in the year of observation if the worker is observed with multiple job spells. We exclude workers in marginal jobs, defined as observations with annual earnings below 50% of the lowest decile cutoff.

Statistical analysis

Our analysis is conducted in two steps. First, to create our dataset, we estimate a series of OLS regression models for each country separately, which report earnings differences of immigrants and children of immigrants relative to natives, considering all world regions of origin combined and separately by world region of origin. Second, we use a meta-analytic approach to summarize the average of these country-specific estimates of immigrant–native earnings differences across all countries and separately by world region of origin. We describe this approach in detail below.

Country-specific regressions

To create our meta-analytic dataset, we estimate a series of OLS regression models using five sequential specifications, following the framework of Penner et al.⁵⁸. These models are estimated separately for each country; this allows us to examine country-specific variation in earnings gaps relative to natives among immigrants and children of immigrants at different levels in the labour market.

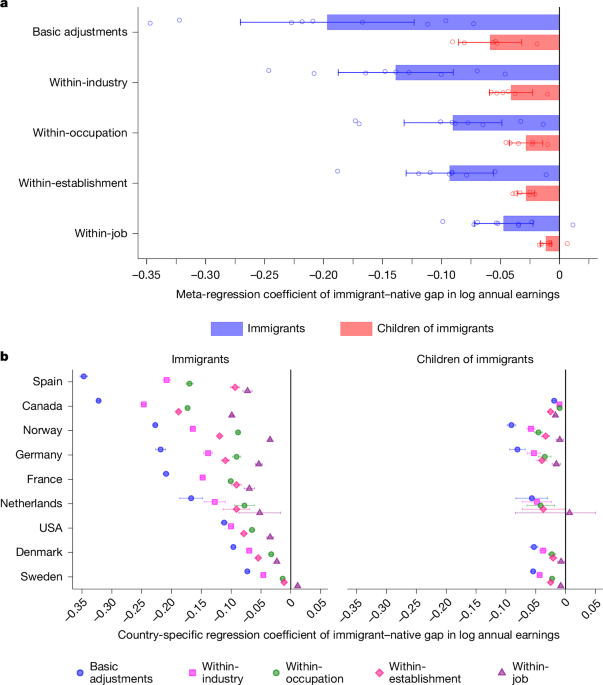
The first model adjusts only for a set of basic covariates (Model 1), providing a baseline estimate of pay gaps between immigrants and natives, and between the native-born children of immigrants and natives. These covariates include educational attainment level, sex, age, and geographic region of employment. This specification provides estimates for the immigrant–native pay gap comparing all workers at the population level, net of basic adjustments for standard human capital controls and unobserved regional labour market characteristics (for example, differences in wage levels between geographic regions). In the subsequent models, we introduce fixed effects that allow us to compare immigrants, children of immigrants, and natives who work in the same industry (Model 2), the same occupation (Model 3), the same establishment (Model 4), and the same job (that is, occupation–establishment unit; Model 5). All models include the basic covariates from Model 1, and comparing the results across these five models enables us to quantify the extent to which immigrant–native differences in earnings are attributable to sorting across industries, occupations, establishments, and specific jobs (occupation–establishment units), relative to within-job pay inequality (that is, different pay for the same job).

The equations estimated for our five core models follow the same general form, using five different specifications:

where the subscripts denote i for individuals, ind for industries, occ for occupations, est for establishments, and occest for occupation–establishment units. The dependent variable is the logarithm of annual earnings (ln(earnings_i)) for individual i and the independent variable I_i is an indicator variable for immigrant background of individual i (coding detailed below), while other covariates are contained in the vector x_i. This vector includes a constant term; the sex, age and age squared of individual i; and a series of indicator variables capturing educational attainment level and geographic region of individual i. The fixed effects η_ind, η_occ, η_est, and η_occest refer to fixed effects for industry, occupation, establishment, and occupation–establishment units, respectively. Our measure of immigrant background (I_i) distinguishes between native workers (the reference category), immigrants, and children of immigrants. In models where we differentiate between the world region of origin of immigrants and children of immigrants, the immigrant background indicators are extended to include categories for world region of origin separately for immigrants and children of immigrants: Asia; Europe, North America, and Other Western; Latin America; Middle East and North Africa; Sub-Saharan Africa.

Model 1 thus provides estimates of the immigrant–native differences in earnings after basic adjustments for sex, age and age squared, education, and geographic region. Model 2 includes these same covariates as well as the fixed effects η_ind representing the industry indicators. Thus, Model 2 provides estimates of immigrant–native differences in earnings obtained from comparing immigrants and children of immigrants to natives who work in the same industry. Intuitively, these results can be thought of as estimating the immigrant–native difference in earnings separately for each industry unit and then taking a weighted average of these immigrant–native differences across all industries. Models 3, 4 and 5 are analogous to Model 2, but contain the fixed effects η_occ, η_est, and η_occest that refer to the unique occupation (η_occ), establishment (η_est), or occupation–establishment (η_occest) unit. The analytic sample for each model is restricted to fixed effect units that are integrated by immigrant background (that is, units that include at least one immigrant or child of immigrants alongside at least one native worker). The subscripts to the γ and θ parameters indicate that these are different coefficients, pertaining to different levels, basic adjustments (BASE), industry (IND), occupation (OCC), establishment (EST) and occupation–establishment (OCCEST).

We use the natural logarithm of earnings as our dependent variable. Following standard conventions, these coefficients on I_i are interpreted as the relative difference on average earnings for immigrants and children of immigrants compared to natives. More formally, our estimates reflect the differences in relative geometric means of unlogged earnings, corresponding to the absolute differences in the arithmetic means of logged earnings⁵⁷.

The country-specific estimates from the five model specifications are presented for immigrants and children of immigrants, both for all groups combined and by world region of origin, separately for each country in the Supplementary Information, section 6 and Supplementary Tables 42–52). The reported coefficients and their corresponding standard errors for each country form the aggregated dataset used in the subsequent meta-analysis.

Meta-analysis of the country-specific regression estimates

Having created our aggregated dataset, we use meta-analysis to analyse the immigrant–native pay gaps across the nine countries. We pool country-specific estimates of differences in earnings between natives and immigrants (and separately, the differences between natives and the children of immigrants) for each of the five regression models described above (Models 1–5). This yields the average immigrant–native earnings difference across all countries, after basic adjustments and within industry, occupation, establishment, and job (occupation–establishment).

The meta-analysis serves two objectives. First, it provides average immigrant–native earnings differences using country-level estimates without differentiating by world region of origin. For each model specification, we include one estimate per country for immigrants (nine countries) and, where information is available, one estimate per country for the children of immigrants (six countries). Second, our meta-analysis provides information on how immigrant–native earnings differences vary by world region of origin, averaged across destination countries we use country-specific estimates differentiating by five world regions for immigrants (45 country–region estimates per model) and for the children of immigrants (30 country–region estimates per model).

To capture sources of cross-country variability, we use a random-effects meta-analysis specification^56,59,60, incorporating a variance component that captures unobserved country-level factors. Random-effects meta-analysis is appropriate when the underlying effect sizes are likely to vary within the population of estimates (that is, we would not expect the country-specific immigrant–native earnings differences to all be identical), rather than representing a single underlying parameter. We specify the random-effects meta-regression models estimated by restricted maximum likelihood, where the general form of this equation is:

where γ_i is the immigrant–native difference in log annual earnings estimated for country i, α is the intercept, μ_i is the random effect for country i, where τ² is the residual between-country variance, and ε_i is the sampling error term with variance σ_i².

To summarize variation in immigrant–native earnings differences by world region of origin averaged across countries, we use in the country–region-specific estimates of immigrant–native differences in log annual earnings. To achieve this, we extend equation (6) by including covariates for world regions, where the equation for the expanded model is:

where γ_k denotes the immigrant–native difference for country–region combination k; β is a vector of coefficients; x_k is a vector of indicators for the five world regions; and μ_k and ε_k are defined analogously as in equation (6).

Figure 1a presents the results from the meta-analysis summarizing the overall pattern of immigrant–native earnings differences, averaged across countries, using the country-specific estimates to fit the model in equation (6). Similarly, Fig. 2a presents corresponding meta-analysis results for immigrant–native earnings differences by world region of origin, averaged across countries, using the country–region-specific estimates to fit the model in equation (7). For all results presented in Figs. 1b and 2b, models are fitted separately for immigrants and children of immigrants across estimates from the five regression specifications. Cochran’s Q, I² and τ² heterogeneity statistics (Supplementary Tables 2 and 4) support the use of random-effects models for the meta-analyses.

Model sensitivity

We also estimated fixed-effect meta-analyses, which assume a common true effect size across studies, to assess the impact of model choice on our results (Supplementary Information, section 2, Supplementary Fig. 2 and Supplementary Tables 8 and 9). To assess whether differences by immigrant generation are sensitive to the sample of countries included, we restricted the random-effects model analysis to the six countries with information about both immigrants and children of immigrants (Supplementary Fig. 1 and Supplementary Tables 6 and 7). In both cases, the results were consistent with our main results.

Statistical software

All analysis was conducted and figures were created using Stata, versions 16–18.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.