High-accuracy laser spectroscopy of $$\bfH_\bf2^\boldsymbol+$$ and the proton–electron mass ratio

Details of the experiment

We use the same apparatus that we used in our previous work²⁰ to perform laser spectroscopy of an E2 transition in \(\rmH_2^+\) and HD⁺. We prepare a cluster of trapped and sympathetically cooled molecular ions, in which the sympathetic cooling is provided by the Coulomb interaction between the molecular ions and the three-dimensional cluster of laser-cooled Be⁺ ions. By loading a small number of molecular ions, they arrange as an ion chain extending along the symmetry axis of the ion trap. The loading occurs by electron impact ionization from background para-H₂ gas. When the direction of propagation of the spectroscopy beam is perpendicular to the chain, a Doppler-free profile can be observed¹⁶.

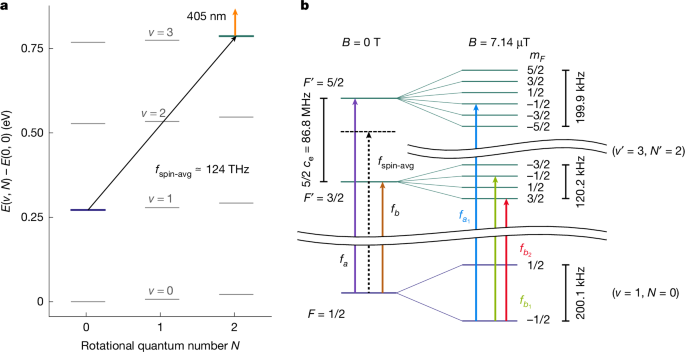
A partial state preparation of the trapped \(\rmH_2^+\) ions is carried out by dissociating those in excited vibrational levels v ≥ 2 (ref. ²⁰), using two lasers at 313 nm and 405 nm. We emphasize that our method does not prepare the population in a specific rotational level.

Following the state preparation, the number of trapped \(\rmH_2^+\) ions is determined by recording the beryllium fluorescence signal accompanying the transverse secular excitation of \(\rmH_2^+\), as a function of excitation frequency. The peak strength of this secular spectrum is proportional to the number of trapped ions. Next, the MHI are subjected to resonance-enhanced, multi-photon dissociation (REMPD). It comprises the excitation of the spectroscopy transition by an optical parametric oscillator (OPO) wave and the dissociation from the upper spectroscopy level by a 405-nm laser wave. To prevent a light shift induced by the dissociation laser, an interleaved shuttering scheme is used. The cycle is concluded with an assessment of the remaining trapped \(\rmH_2^+\) ions. Subsequent cycles alternate between spectroscopy and background measurements (in which the spectroscopy laser is blocked) until sufficient statistics have been gathered. Between cycles, the ion cluster is purged of ions other than Be⁺ and a new \(\rmH_2^+\) ensemble is loaded to ensure that the lower spectroscopy level has sufficient population. Throughout the REMPD, a magnetic field of B_REMPD ≃ 7.14(4) μT was applied, determined as explained in a later section. The spectroscopic signal is derived by comparing the number of trapped \(\rmH_2^+\) ions before and after REMPD. This is computed as the normalized decrease in the ion number.

The spectroscopy laser system has been described previously²⁰. We use the idler wave of the OPO as the spectroscopy wave that is stabilized in frequency by referencing it to an ultrastable optical frequency comb²⁷. The upper-bound linewidth of the idler wave depends on the reference laser used for the optical frequency comb. Over the course of the data acquisition, two different reference lasers were used. Characterization showed that they produce a spectroscopy wave linewidth of approximately 5 Hz and 20 Hz, respectively, on timescales of 1–10³ s. The measurements acquired under nominal conditions and at high-trap RF amplitude were taken with a 20 Hz linewidth. All other systematic measurements (Supplementary Information) were obtained with a 5-Hz spectroscopy wave linewidth. As this linewidth is moderately smaller than the observed linewidths, it seems to contribute to the observed molecular transition linewidths. For long-term frequency stability, the optical frequency comb is referenced to a hydrogen maser. Furthermore, we compare our hydrogen maser with the German national standard using Global Navigation Satellite System (GNSS), thereby ensuring Système-International-traceability of the frequency of the spectroscopy wave. The combined frequency error of the spectroscopy wave for timescales of one REMPD cycle is ≤1 Hz, or ≤1 × 10⁻¹⁴ in relative terms. This includes fluctuations of the laser, statistical errors of the frequency comb measurement and maser frequency corrections (see section ‘Maser shift’).

We deliberately performed a blind experimental search of the transitions, using a value of \(f_\textspin-avg^(\rmtheor)\) as input information with an added offset that turned out to be approximately 80 kHz after unblinding. The narrow linewidth of the transitions and the large Zeeman shifts of the components rendered their discovery tedious. \(f_\textspin-avg^(\rmtheor)\) as reported above was disclosed only after completion of all measurements. Its value was taken into account to identify the observed transitions, which is a necessary step for performing the complete analysis.

Systematics of the \(\bfH_\bf2^\boldsymbol+\) E2 transition

We have measured all systematics effects that we believe to be of significant magnitude compared with our spectroscopic resolution. For each shift, the measurements have been done on a subset of the three Zeeman components \(f_a_1\), \(f_b_1\) and \(f_b_2\). Figures of the corresponding lines are shown in the Supplementary Information. In total, we have measured 11 individual lines, 4 of which were under nominal conditions (Fig. 2). The remaining lines were Zeeman components perturbed by a single parameter setting (a laser intensity or the RF amplitude of the trap). To evaluate all systematic effects as well as \(f_\textspin-avg^(\rme\rmx\rmp\rmt)\) and \(c_\rme^(\rmexpt)\) we performed an adjustment to all observed lines (see section ‘Evaluation of deperturbed values \(f_\textspin-avg^(\rmexpt)\) and \(c_\rme^(\rmexpt)\)’). Below, we first enumerate the shifts that we considered and subsequently discuss the adjustment.

Zeeman shift

To determine the Zeeman shifts of the components, we rely on theoretical results^28,53. The three measured components have substantial linear and small quadratic shifts. The predicted shift coefficients are \(c_\rml\rmi\rmn,a_1=11.2\,\rmk\rmH\rmz\,\rm\mu T^-1\), \(c_\rml\rmi\rmn,b_1=16.8\,\rmk\rmH\rmz\,\rm\mu T^-1\), \(c_\rml\rmi\rmn,b_2=5.6\,\rmk\rmH\rmz\,\rm\mu T^-1\), \(c_\rmq\rmu\rma\rmd,a_1=2.2\,\rmk\rmH\rmz\,\rm\mu T^-2\), \(c_\rmq\rmu\rma\rmd,b_1=-2.2\,\rmk\rmH\rmz\,\rm\mu T^-2\), \(c_\rmq\rmu\rma\rmd,b_2=-1.4\,\rmk\rmH\rmz\,\rm\mu T^-2\). In section ‘Evaluation of deperturbed values \(f_\textspin-avg^(\rmexpt)\) and \(c_\rme^\text(expt)\)’, we use these coefficients as input parameters in the determination of the Zeeman shifts and treat the magnetic field value B as an adjustable parameter. The adjusted value B_REMPD ≃ 7.14(4) μT is in agreement with, but more precise than, the value determined in our previous spectroscopy experiments on HD⁺.

As our total measurement duration extended over several months, the long-term stability of the magnetic field was verified. Measurements of one line, performed a few months apart, yielded no observable frequency shift within experimental uncertainty. Considering the above Zeeman coefficients, we deduce a mean drift rate below 19 pT day⁻¹. This bound has an insignificant impact compared with our overall measurement uncertainty.

The a.c. and d.c. Stark shifts

During the REMPD, two laser waves were present: the spectroscopy wave (2.4 μm) and the Doppler cooling wave (313 nm). These cause a.c. Stark shifts (light shifts) of the transition frequencies.

We have, therefore, measured the component \(f_a_1\) at two different intensities of the spectroscopy wave (Supplementary Fig. 2). The a.c. Stark shift of other components are determined relative to this measurement by making use of the ratios of theoretically calculated polarizabilities (see section ‘Evaluation of deperturbed values \(f_\textspin-avg^(\rmexpt)\) and \(c_\rme^\text(expt)\)’).

We remark that alternatively, an estimate for the shift can be obtained from the theoretical polarizabilities⁵⁴ and an approximate value for the spectroscopy wave intensity. This estimate gives maximum 2.4-μm-light shifts of the order of −60 Hz for both components f_a and f_b, consistent with our observation, but one order smaller than the bounds resulting from our evaluation (Table 2). However, we take a conservative approach, relying more on our experimental data.

Regarding the shift caused by the 313-nm wave, we have measured two components, \(f_a_1\) and \(f_b_1\), at three intensities each. The more detailed investigation of this shift was motivated by the large observed dependence on 313 nm wave intensity. For this wave, we similarly use theoretical polarizabilities to infer the shifts not directly measured.

Moreover, we assume a linear dependence of the transition frequencies on both wave intensities, with common sensitivity parameters k₃₁₃ and k_2.4 for all components (see section ‘Evaluation of deperturbed values \(f_\textspin-avg^(\rmexpt)\) and \(c_\rme^\text(expt)\)’).

We have not measured the shift of the transition frequency arising from a spatial offset of the \(\rmH_2^+\) ensemble relative to the nominal location in the trap. This effect is expected to be negligible, given that the trap is well compensated and that the residual static electric field is small. This expectation is supported by the fact that we have previously investigated the d.c. Stark effect in HD⁺ E2 transitions, and we have not resolved any shift at the level of 90 Hz (ref. ²⁰), and that the static polarizability of the present \(\rmH_2^+\) transition is more than two orders of magnitude smaller than that of the HD⁺ transition⁵⁴. For these reasons, we expect the trap offset effect to be negligible and assign it a zero value and uncertainty.

Radiofrequency trap shift

We have measured the transition frequency \(f_a_1\) at two different trap RF amplitudes. In contrast to HD⁺, in which for an E2 transition we observed shifts of approximately 1.2 kHz for two equivalent Zeeman components of the studied spin component²⁰, here we did not resolve a shift. Although a possible shift would increase with increasing RF amplitude, we were unable to perform measurements at RF amplitudes larger or smaller than those presented, because the background loss of the trapped \(\rmH_2^+\) ensemble then increases. The non-observation of a shift confirms our earlier hypothesis²⁰ that the trap-field-induced shift is smaller for homonuclear MHIs compared with heteronuclear MHIs, because of the absence of off-resonant electric dipole coupling between each spectroscopy level and other rovibrational levels. However, electric dipole couplings to excited electronic states of \(\rmH_2^+\) are nonzero. Therefore, a shift could still occur, but of much smaller magnitude. Therefore, we model the RF trap shift, similarly to the a.c. Stark shifts above, by the use of theoretical polarizabilities, an overall sensitivity parameter k_RF and a quadratic dependence on the RF amplitude of the trap. The quadratic dependence is known from previous experiments²⁰.

Autler–Townes splitting or a.c. Stark splitting

The upper spectroscopy level interacts with two light fields, 2.4 μm and 313 nm, where the latter couples to the continuum. We, therefore, observe a splitting of the line \(f_a_1\). This is known as the Autler–Townes effect (or a.c. Stark splitting)⁵⁵ and has earlier been observed for multi-photon processes in strong laser fields, both continuous-wave and pulsed. For the case of HD⁺, we have previously investigated this effect in our apparatus and determined a square-root dependence on the UV-laser intensity (see Supplementary Information section E), consistent with reports in the literature^56,57. We have measured the splitting of component \(f_a_1\), for nominal and high trap RF amplitudes. Both observed splittings agree within the combined uncertainties. The mean amounts to \(\Delta f_\rmAT,nom,a_1=195(15)\,\rmHz\) at the nominal 313 nm intensity I_313,nom. We assume that the ratio \(\Delta f_\rmAT/\sqrtI_313=\Delta f_\rmAT,\rmnom,a_1/\sqrtI_313,\rmnom\) is the same for all lines.

Black-body radiation shift

The black-body radiation shift of \(\rmH_2^+\) is predicted to be of the order of 10⁻¹⁷ fractionally at room temperature⁵⁴ and is ignored.

Maser shift

As in our previous works^13,15,16,20, the frequency of the spectroscopy wave is measured relative to the 5 MHz output of a hydrogen maser. This frequency is continuously compared with a 1 pulse-per-second signal provided by a GNSS receiver. Common-view GNSS data allow us to determine the maser frequency with respect to the German national time standard. We determined the fractional frequency offset of the maser to be approximately +1 × 10⁻¹¹, and the fractional drift was approximately +3 × 10⁻¹⁵ day⁻¹. The measured laser frequencies are corrected for the time-varying maser offset. The uncertainty of this correction was determined to be approximately 10 mHz.

Recoil shift

This is discussed in Supplementary Information section E.3.

Evaluation of deperturbed values \(\boldsymbolf_\bfs\bfp\bfi\bfn\boldsymbol\mbox–\bfa\bfv\bfg^\bf(e\bfx\bfp\bft)\) and \(\boldsymbolc_\bfe^\bf(e\bfx\bfp\bft)\)

The determination of the quantities of interest in the presence of the above systematic effects is performed by an LSA. To this end, we model a measured transition frequency j as follows:

The dotted equality sign means that the left and right hand sides should agree within estimated uncertainties. The subscript i refers to both a particular spin-rotation component and a particular Zeeman component. The index j denotes individual measurements, that is, for a given i, the superscript j may take on different values. \(f_\rmobs,i^(j)\) is the measured line frequency with a statistical uncertainty given by the half width at half maximum of the line and \(\delta f_\rmA\rmT^(j)\) is its shift due to the Autler–Townes effect. The spin coefficients of the upper spectroscopy level are \(c_\rmspin,i=(F_i^\prime (F_i^\prime +1)-N(N+1)-3/4)/2\) (see main text) and the Zeeman coefficients c_lin,i, c_quad,i of component i are taken to be the theoretical values (see section ‘Zeeman shift’).

For each systematic shift, we define the contribution as \(\delta f_\rmeffect,i^(j)\,=\,\)\(r_\rmeffect,ik_\rmeffectQ_\rmeffect^(j)\), with the relative sensitivity r_effect,i of a spin-rotation Zeeman component i and the global sensitivity k_effect of the rovibrational transition. The parameter \(Q_\rme\mathrmffect^(j)\) is one of the following: the spectroscopy wave power, \(P_2.4^(j)\), the Doppler cooling wave power \(P_313^(j)\) or the squared trap RF amplitude \((V_\rmRF^(j))^2\). The parameters k_effect must be adjusted by the LSA, because we do not know the precise light intensities and electric fields at the locations of the ions.

The values r_effect,i are computed as the ratios of theoretical polarizabilities of the Zeeman components⁵⁴. The total polarizability of a component is the sum of a scalar (spin-independent) polarizability α_s and a tensor polarizability, where the latter can be expressed as a spin-independent value α_t multiplied by a state-dependent factor S and a polarization-dependent factor G. The tensor polarizability is zero when N = 0; hence, it is zero in the lower spectroscopic states. We have \(S(f_a_1\,)=-\,24/5\), \(S(f_b_1\,)=-\,21/5\) and \(S(f_b_2\,)=21/5\). To compute the total polarizability of the transitions, it is necessary to combine the values of the scalar and tensor polarizabilities of the lower and upper levels. Note that the r_i,effect of the same component i are distinct for different effects, because the scalar and tensor polarizabilities are, in general, frequency-dependent. For the case of the RF and 2.4 μm fields, the polarizabilities can be found in refs. ^20,54, respectively, whereas for the 313 nm field, we have computed them to be α_s(v′ = 3, N′ = 2) − α_s(v = 1, N = 0) = 6.9 a.u. and α_t(v′ = 3, N′ = 2)= −1.3 a.u. A table of numerical values r_effect,i used in the adjustment can be found in Supplementary Table 1.

To perform the LSA, the equations should be linearized. The only non-linear contribution is the quadratic Zeeman shift. We linearize the equations by expressing the magnetic field B_REMPD = B₀ + δB as the sum of a constant value B₀, approximately known from previous experiments, and an adjustable small deviation δB. The term quadratic in δB may safely be neglected.

In summary, the LSA includes 11 observational equations to which six parameters are adjusted, \(f_\textspin-avg^(\rmexpt)\), \(c_\rme^(\rmexpt)\), δB, k_2.4, k₃₁₃ and k_RF. All input data are uncorrelated.

The Autler–Townes effect is not considered in the same form as the other systematic effects, because it is a splitting rather than a shift. For those lines, for which we have measured the splitting (note that for these \(I_313^(j)=I_313,\rmnom\)), the shift is simply given by half the observed splitting, \(\delta f_\rmAT^(j)=\mp 1/2\Delta f_\rmAT,\rmnom\). Positive and negative signs correspond to the smaller and larger frequency components, respectively. For the other lines, we present two approaches for accounting for the effect.

In approach 1, as the sign of \(\delta f_\rmAT^(j)\) is unknown for these cases, we set \(\delta f_\rmAT^(j)=0\), but with uncertainty \(u(\delta f_\rmAT^(j))=\Delta f_\rmAT^(j)/2\). Furthermore, the scaling with intensity is \(\Delta f_\rmAT^(j)=\sqrtI_313^(j)/I_313,\rmnom\times \Delta f_\rmAT,\rmnom,a_1\). As \(\Delta f_\rmAT,\rmnom,a_1\) is much larger than the statistical uncertainty of the lines, and combined with the fact that our measurements can resolve a shift neither due to I_2.4 nor due to V_RF, the resulting uncertainty of \(f_\rms\rmp\rmi\rmn\,-\,\rma\rmv\rmg^(\rme\rmx\rmp\rmt)\) and \(c_\rme^(\rme\rmx\rmp\rmt)\) far exceeds our line resolution. The values presented in the main text result from this approach. The values of systematic shifts of individual Zeeman components \(\delta f_\rme\rmff\rme\rmc\rmt^(j)\) given in Table 2 are computed using the resulting sensitivities k_effect.

Approach 2 is described in the Supplementary Information.

Ab initio theory of f
_spin-avg

Theoretical data have been obtained in two steps. First, the spin-averaged transition frequency was calculated as an expansion in terms of the coupling parameter, the fine structure constant α. We started from the nonrelativistic solution of the Schrödinger equation. Second, higher-order corrections were obtained in a perturbative way along the lines of the NRQED effective field theory⁷. The individual contributions are: f⁽⁰⁾ = 124,485,554,550.71 kHz (nonrelativistic three-body Schrödinger solution), f⁽²⁾ = 2,002,698.73 kHz (relativistic corrections in the Breit–Pauli approximation; nuclear radii), f⁽³⁾ = −521,345.53 kHz (leading-order one-loop radiative corrections), f⁽⁴⁾ = −3,689.05 kHz (one- and two-loop radiative corrections; relativistic corrections), f⁽⁵⁾ = 228.67 kHz (radiative corrections up to three loops, Wichmann–Kroll contribution), f⁽⁶⁾ = −1.62 kHz (one- and two-loop radiative diagrams, Wichmann–Kroll contribution), f^other = 0.54 kHz (muon and hadron vacuum polarization). Here, f⁽ⁿ⁾ denotes a contribution proportional to cR_∞αⁿ. The sum of all these contributions, \(f_\textspin-avg^(\rmtheor)\), together with the theoretical uncertainty, is given in the main text. The above values are for CODATA 2022.

The sensitivity of the spin-averaged frequency to m_p/m_e has been reported in ref. ²⁰, ∂f_spin-avg/∂(m_p/m_e) = −0.43976 × f_spin-avg/(m_p/m_e).

In the computation of the QED theory uncertainty of the frequency ratios, correlation coefficients and uncertainties proposed by J.-Ph. Karr have been used.

Ab initio theory of the spin–rotation coupling

\(c_\rme^(\rmtheor)\), given in the main text, is calculated theoretically using the Breit–Pauli Hamiltonian and then including higher-order corrections up to order mα⁷ln α. When higher-order corrections are considered, other spin interaction terms may also appear, for example, proportional to I₁ ⋅ I₂. First, they are a factor \(\alpha ^2(m_\rme/m_\rmp)^2\) smaller than the leading-order hyperfine structure splitting of the state. Second, the total nuclear spin in every rotational state N is fixed and thus also the value of I₁ ⋅ I₂ is uniquely determined. This means that these new terms do not contribute to the splitting, but to the spin-averaged energy. They are included in f⁽⁴⁾ above.

Ab initio theory of the Zeeman interaction

The interaction of para-\(\rmH_2^+\) with an external magnetic field is described by the effective Hamiltonian:

where μ_B = |e|ħ/(2m_ec) is the Bohr magneton, g_N(v, N) is the orbital g-factor and g_e(v, N) ≃ −2.002319 is the bound-electron g-factor. The anisotropy of g_e is neglected. g_N is calculated numerically from the nonrelativistic three-body-bound-state wave function⁵⁸. For the upper level of the transition, g_N(v = 3, N = 2) = 0.48156 × 10⁻³. The computation of the Zeeman shifts is given in the Supplementary Material of ref. ¹.