Goal-specific hippocampal inhibition gates learning

Animals

All procedures involving animals were performed in accordance with the guidelines provided by the Institutional Animal Care and Use Committee at the Georgia Institute of Technology. Our study used C57BL/6J adult male WT mice (n = 9 mice) and PVxAi32 mice (n = 11 mice) at 10–12 weeks of age (3.5–5 months at the time of the recordings). For optogenetics experiments, we crossed male PV-Cre knockin (The Jackson Laboratory, 017320) mice with female homozygous Ai32 mice (The Jackson Laboratory, 024109) to generate PVxAi32 mice (n = 11 mice) that express ChR2 specifically in PV-positive interneurons. The mice were housed in a reverse dark–light-cycle room (07:00 light off, 19:00 light on) with ad libitum access to food and water. Animal housing rooms are equipped with a ventilation system that provides 12 air changes per hour, temperature range of 64–79 °F and 30–70% relative humidity. We performed all behavioural training during the dark cycle. Sample sizes were determined based on sample sizes used in previous studies^23,24,42. We aimed for sample sizes of 5–7 mice per group with a large number of single units per animal. No power analysis was performed. Owing to the nature of experiment monitoring during electrophysiology recording, the experimenter could not be blinded to the condition. Experimenters were blinded to stimulation and novelty conditions for analyses. We used a within-subject design, in which individual animals were exposed to both conditions (novel and familiar or goal and sham stimulation), thus randomization to groups was not relevant.

Graphical illustrations of a mouse in VR were created by B. Mariner for the Singer laboratory. The drawing of mouse head profile (E. Tyler and L. Kravitz, mouse drinking, Zenodo, https://doi.org/10.5281/zenodo.3925985) and brain (F. Claudi, mouse brain sagittal, Zenodo, https://doi.org/10.5281/zenodo.3925911) were adapted from scidraw.io.

Surgery

Mice were handled for at least 3 days before stereotaxic surgery. For head-plate implantations, mice were deeply anaesthetized with isoflurane, and head-plates were affixed to the skull with dental cement (Parkell C&B Metabond). For acute extracellular recordings, craniotomies of 600–900 µm in diameter were made on either hemisphere of well-trained mice 1 day before the first recording. We used the following coordinates to target CA3 stratum pyramidale (from bregma): −1.8 mm anteroposterior (AP), 2.4 mm mediolateral (ML) and about 2.5 mm dorsoventral (DV).

VR spatial-learning task

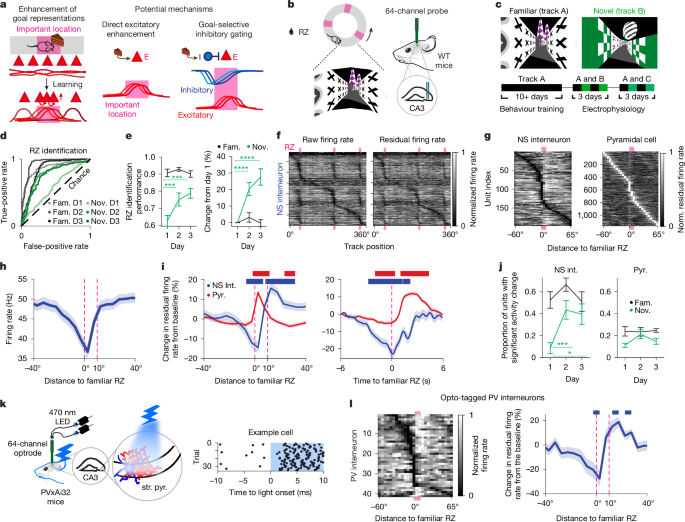
Mice began habituation to head fixation on a treadmill at least 7 days after head-plate implantation. We trained mice to run on either a linear treadmill (n = 4 WT mice; PhenoSys SpeedBelt) or a spherical Styrofoam treadmill floating on air (n = 5 WT mice, 11 PVxAi32 mice) to determine whether changes in interneuron activity were consistent across systems. To increase motivation for running, animals were food-deprived gradually to 85–90% of their original body weight. Mice were head-fixed and trained daily to run unidirectionally on the virtual track for progressively longer periods. Mice received drops of sweetened condensed milk as a reward, delivered through a plastic needle. Licks were detected using either a piezoelectric sensor attached to the reward needle or a custom-built photointerruptor-based system. All virtual tracks were designed and interfaced with animals using the open-source software Virtual Reality MATLAB Engine (ViRMEn) open-source software (in MATLAB v.2015b) as previously described⁵¹. Proximal and distal cues were projected onto a cylindrical screen, creating a rich and immersive environment for virtual navigation. Voluntary movement of a mouse on the linear or spherical treadmill automatically advanced movement in the virtual track environment.

We used three annular tracks (tracks A, B and C; Fig. 1c) of the same size but with distinct visual cues, reward locations and distances between the reward locations. All of the mice were initially trained on track A as the familiar environment and later during recordings were introduced to tracks B and C (not shown) as the novel condition. Speed gain was set such that 1° advancement through the virtual environment was equivalent to the movement of about 1.5 cm on the belt for a total distance of approximately 540 cm around each track. Animals completed a full lap (360°) in 66 s on average (range of 12–346 s). Gain on the spherical treadmill was adjusted to ensure similar virtual experience as with the linear treadmill. Each of the tracks had 36 non-overlapping, equally sized wall cues (10° per cue), and three of them were associated with reward (RZs, each 10°). The RZs were irregularly placed to prevent animals from solely using the inter-reward distances to perform the task across multiple environments.

For the first 3–5 days of training in the virtual environment, mice received rewards automatically when they arrived at the three RZs on the track. After this first phase of training, the mice showed anticipatory licking immediately before the reward delivery. In the subsequent training and recording sessions, the mice were required to lick in the RZs to trigger a reward delivery. To prevent generalized licking irrespective of position on training days, licking more than 25–50 times cumulatively outside the anticipatory and RZs triggered a 4-s time-out period. During a time-out period, the animal was teleported to a grey box and received no reward. After 4 s, the mouse resumed running from the location it had left off before the time-out. We introduced mice to novel tracks on days of recording only after a mouse was deemed to have learned and reached behavioural criteria indicative of good performance in the familiar environment. Mice were required to have 85% correct or higher performance in the familiar environment for at least two consecutive sessions before recording commenced. Behavioural performance criteria were set based on an animal’s propensity to slow down and lick more in the AZs.

Behavioural data analysis

Raw behavioural data were divided based on an animal’s position (in degrees) into either 360° laps around the whole environment or RZ-centred trials that spanned the area 60° before and after each 10° RZ for analyses. Mean speed (in ° s⁻¹) was calculated by dividing the total distance travelled in each 2° position bin by the total time spent in that bin. The lick probability was calculated by taking the ratio of the number of licks per position bin over the total number of licks within the lap or trial. The lick rate (in licks per s) was calculated by dividing the number of total licks per position by the total time spent in that bin over all position bins. Speed and lick behaviour for each lap or trial was smoothed with a Gaussian-weighted moving-average filter (s.d. = 2 bins). Once learned, mice tended to show stereotypical behaviour in all three RZs. Thus, speed and lick behavioural data around all three RZs were concatenated and averaged for each session. We used ROC curves to quantify behavioural performance based on how well mice differentiated between the pre-RZ (AZ) and the non-reward control zone that appeared 30° after the end of each RZ. For lick-latency-based performance, we quantified the time between when an animal entered the RZ and the first lick compared with the control lick latency at the NRZ. We quantified learning over days using area under the receiver-operating characteristic curves in which larger AUC values indicate better behavioural performance. The performance metric using movement speed data tended to be better at position differentiation than licking-based metrics, probably because mice were not required to lick in the AZ to receive a reward and well-trained animals licked very sparsely (Extended Data Fig. 1e).

Electrophysiology

All extracellular electrophysiology recordings were performed using a poly 5 two-shank 64-channel silicone probe or a 64-channel optoelectrode of the same channel geometry (NeuroNexus). Neural data were acquired using either two 32-channel Upright Headstages with Trodes software (v.2-2-3, SpikeGadgets) or two RHD 32-Channel Recording Headstages and Intan RHD2000 Evaluation system (version 1.5.4 with MATLAB file read_Intan_RHD2000_file v.2.0, Intan) at a sampling rate of 30 kHz with a ground pellet used as reference. The location was determined by stereotaxic coordinates, depth and electrophysiological signatures. Electrophysiological features indicative of the CA3 were closely monitored: high-amplitude theta activity during running, prominent sharp-wave ripples during stillness and high-amplitude (100 + µV) action potentials appearing on many channels.

Each recording day consisted of at least two sessions of 15 to 30 min in the familiar (track A) and novel (track B or C) environments (always starting with the familiar environment). Behavioural sessions in the VR environment were separated by a shorter (5–10 min) baseline recording period in the dark. The movement direction was consistent (clockwise) across environments. We performed recordings from the same craniotomy (typically from the right hemisphere first) for three consecutive days, using the same novel track during this period. After the first set of novel learning days, a second craniotomy was made on the contralateral hemisphere on the fourth or fifth day, and mice learned a brand new track for three consecutive days starting on the following day (details on the number of cells recorded per mouse are provided in Supplementary Tables 1 and 2).

Optogenetic stimulation during behaviour

We recorded and stimulated neural activity simultaneously using a customized two-shank 64-channel optoelectrode with two optical fibres terminating 100–200 µm above the top recording site on each shank. Ferrule patch cables (Ø105 µm core, 0.22 NA SMA905 to Ø1.25 mm; Thorlabs, M63L01) were connected to optical fibres on one end through ceramic split mating sleeves (Thorlabs, ADAL1-5) and 470-nm fibre-coupled LEDs (Thorlabs, M470F3) with T-Cube LED driver (Thorlabs, LEDD1B) with a 15 V power supply unit (Thorlabs, KPS101) on the other end. This approach delivered truncated cones of light in the dorsal CA3 that were approximately 2 mm³. On the basis of light spread and attenuation measured in brain tissue in previous work, we estimate a volume of 0.005–0.02 mm³ received light at intensities needed to drive channelrhodopsin (greater than 1 mW mm⁻²)^52,53. Previous studies estimate between 500 and 2,500 PV cells per mm³ in the CA3 (refs. ^54,55). We confirmed the optical targeting of 2–3 PV units on average in a single recording. Consistent with light-induced activation, we observed an increase in PV firing activity within around 3 ms of blue LED light (470 nm) onset (Supplementary Fig. 2c). We controlled the onset, offset and intensity of blue light with a National Instruments data acquisition system and custom MATLAB code. Both fibres were illuminated at the same time and intensity. Position-specific stimulation was triggered in real time by animal position in the virtual environment. In the goal location-specific condition (goal stimulation), light turned on when an animal entered the AZ, the zone immediately before the RZ and stayed on for up to 10 s or until the animal left the RZ, whichever came first. In the sham stimulation condition, the light turned on when the animal entered the NRZ and stayed on for up to 10 s or until the animal left the zone immediately after the NRZ. Sham stimulation controlled for non-specific effects of optogenetic stimulation and for the effects of PV activity on novelty in general as both types of stimulation were in novel environments. A subset of animals was stimulated at the anticipatory or RZ only, or for a fixed duration of 3 s regardless of position. For each of the three stimulation zones, we stimulated at the light intensity of either 0, 5 or 13 mW mm⁻², referred to as no-stim, low-stim or high-stim, respectively, from the fibre tip. The stimulation intensity remained the same for each goal location in the same novel environment over 3 days. We randomized the order of stimulation intensities across three stimulated areas in each environment across animals. Each stimulation session consisted of 20 min of stimulation trials followed by 5 min of stimulation-free trials to assess the potentially lasting effects of stimulation at the end of a session. To examine the effects of goal stimulation in the familiar environment, all PVxAi32 mice received a shorter (about 10 min) session with goal location-specific stimulation trials in the familiar environment (track A) as their final session of the last day of recording.

Behaviour and recording in Y-maze with update cue

To test flexible decision-making in rodents in response to new information, we designed a VR update task that requires animals to perform a memory-guided decision-making task. On most trials, the task presents animals with an initial visual cue that indicates the correct goal location in a Y-maze environment, and the animals must then run down the track to the correct arm to receive a reward. On a subset of trials, a second visual cue appears that indicates that the reward location has either changed (switch trials) or stayed the same (stay trials). On these trials, the mice must choose to keep their original goal destination or switch to the other goal destination. The mice were rewarded at the end of the track if they selected the correct arm, followed by a VR screen freeze for 3 s and then an intertrial interval period of 6 s with a grey screen. On incorrect trials, no reward was delivered and the intertrial interval was 12 s, a longer interval as a form of punishment. Over the course of a session, animals successfully performed the behaviour across all trial types.

Behaviour training and recording methods are described in detail previously⁴¹. Additional eight-week-old C57Bl/6 WT mice (n = 7) were implanted and recovered as described above. Over a period of about 8 weeks (55.43 ± 7.38 days of training, mean ± s.e.m.), food-restricted mice underwent several phases of training for about 1 h per day 5–7 days per week to ultimately learn the task. In brief, animals first learned to run on a linear track, then trained in a short Y-maze, followed by a long Y-maze. In the Y-maze, the visual cues on the walls indicated which goal arm was rewarded. At first, the cues were visible for the entire track. A delay was then introduced between the cue turning off and the choice point when animals had to select a goal arm. This delay got progressively longer. After animals performed well with a long delay, the update cue was introduced. After animals demonstrated mastery of the task with the update cue, recordings were made in CA1 using a 64-channel, dual-shank NeuroNexus probe (targeting −1.8 to –2.0 mm AP, 1.5–1.8 mm ML and about 1.4 mm DV). Recordings were made over 6–12 session per animal (details on the number of cells recorded and trial types performed per animal are provided in Supplementary Table 3). Data were analysed as described above. The RZ onset was defined as when the animal received reward, and the update cue onset was defined as when the update cue was presented.

Histological verification of the probe location

On the last day of recording, the neural probe was dipped in fluorescent dye diI (0.9 mg ml⁻¹) before recording. After recording, the mice were deeply anaesthetized with isoflurane and perfused with 4% paraformaldehyde. The brains were extracted and drop-fixed in 4% paraformaldehyde for 24 h then rinsed in 1× phosphate-buffered saline (PBS) and either sectioned by a vibratome or cryoprotected in 20% sucrose solution overnight before being frozen for sectioning on a cryostat. Fixed brain tissues were cut coronally on a vibratome or a cryostat. Tissue sections were stained for nuclei with DAPI, mounted (Vectashield Antifade Mounting Media) and confocal imaged at ×10 using the LSM 700 laser-scanning confocal microscope (Zeiss).

VR screen freeze manipulation at RZs

A small group of animals (n = 4) was exposed to a behavioural manipulation in VR on the last recording day to control for position-dependent changes in speed and licking activity. In this session, we introduced an automatic screen freeze at the three RZs in the familiar environment for a fixed duration of 3 to 10 s regardless of the animal’s movement on the ball. The goal of this manipulation was to dissociate movement speed from position-specific visual cues. After VR manipulation, we examined the effects of distinct visual cues on firing rates of the same neurons within the same animals at similar running speeds and licking activity.

Preprocessing of LFPs and detection of sharp-wave ripples and theta periods

To obtain LFPs, recorded signals were downsampled to 2 kHz, band-pass filtered between 1 and 300 Hz and interpolated over outliers (noise) defined as 15 s.d. above the mean of the prefiltered signal. In all of our LFP analyses, we used the channel with the highest envelope amplitude for the ripple band signal as the proxy site of the stratum pyramidale⁵⁶. For analyses of theta, gamma and SWR periods, the LFP was band-pass-filtered based on frequency bands (4–12 Hz for theta, 1–4 Hz for delta, 12–30 for beta and 125–250 Hz for SWR) using a finite impulse response equiripple filter. SWR events were detected when the envelope amplitude of the filtered SWR trace (125–250 Hz) was greater than 3 s.d. above the mean for at least 20 ms (refs. ^12,57,58). We excluded any events with a power ratio (power from 100 to 250 Hz/power from 250 to 400 Hz) less than four based on the typically observed frequency range of SWRs⁵⁹. We only included in our ripple analyses the periods with at least one multi-unit spike and excluded periods during which the movement speed was above 5° s⁻¹ during the 2-s time window, 1 s before and after the mid-point of each SWR event. Multi-unit spikes were extracted by band-pass filtering the raw recorded signal between 300 and 6,000 Hz and thresholding the filtered signal above 5 s.d. from the mean. Extracted periods of interest were then visually inspected to ensure accurate detection. The duration of SWRs was defined as the length of time that the SWR envelope was greater than the threshold of 3 s.d. above the mean. SWR power was quantified as s.d. above the mean ripple power for the entire recording session. The SWR rate was quantified by dividing the total number of SWR events by the total duration of stopped periods (movement speed fell below 2° s⁻¹ for at least 2 s) for individual recording sessions with at least ten ripples detected. Coactivation probability during SWRs was defined as the number of SWRs during which both neurons in a pair had spikes, divided by the total number of SWRs⁵⁸. To show the spread of data with individual datapoints, we used violin plots. Violin plots show the kernel density estimate of the distribution (lighter shaded area), individual data points (coloured circles) and box plot indicating the median (white circle), first and third quartiles (thicker lines) and 1.5× the interquartile range (whiskers).

Single-unit isolation

We identified and sorted putative single units using the automatic clustering software Kilosort2⁶⁰, followed by visualization and manual curation using Phy 2.0. Only well-isolated units with the signal-to-noise ratio of greater than 1 and <0.01% refractory period violations (interspike interval < 1 ms) were included in the study. We visually verified the firing rate stability of single units by ensuring the firing rates during periods in between VR sessions did not fall below the threshold set at 10% of the peak firing rate of the entire duration of the recording.

Cell-type classification

We classified single units as pyramidal cells and interneurons with narrow and wide waveforms based on the spike waveform’s trough-to-peak latency, inter-spike interval statistics such as burst index¹⁵ and the autocorrelogram (ACG) fitted with a triple-exponential equation using CellExplorer (v.1.2) software⁶¹:

where c is the ACG τ decay amplitude, d is the ACG τ rise amplitude, h is the burst amplitude and t_refrac is the ACG refractory period (ms). The CellExplorer software automatically identifies putative NS interneurons with trough-to-peak latency ≤ 0.425 ms, wide spike-width (WS) interneurons with trough-to-peak latency > 0.425 ms and ACG τ rise amplitude > 6 ms and the remaining units assigned as pyramidal cells. We visualized all pre-labelled units, and manually excluded bad units or relabelled a cell type based on the ACG and firing characteristics. This process led to some overlap in the distributions of identified cell types, consistent with examples in CellExplorer. We recorded a total of 3,489 well-isolated single units recorded in this study (Supplementary Fig. 1). Among these, we identified a total of 437 NS interneurons, 254 WS interneurons and 2,798 pyramidal cells. We confirmed that PV interneurons verified by opto-tagging had similar waveform properties and firing rates to NS interneurons that we recorded. To identify optically tagged PV-positive interneurons, we used the stimulus-associated spike latency test as previously described⁶² and performed manual verification by visualizing light-evoked firing activity within 1–3 ms of light onset. Putative PV cells in WT animals were identified as NS interneurons with mean firing rate greater than lowest quarter of opto-tagged PV cells in familiar environment (about 20.1 Hz) to capture the population of fast-spiking interneurons contributing to behaviourally relevant network oscillations like theta (intrinsic firing rate, 21 ± 5 Hz)⁶³, gamma (intrinsic firing rate, 32.70 ± 0.793 Hz)⁶⁴ and SWRs (intrinsic firing rate, 122 ± 32 Hz)⁶³.

Previous work has shown that different subtypes of NS interneurons in hippocampus have different firing patterns in relation to theta oscillations and SWRs^27,28,29,30. Thus, to investigate how reward-related firing patterns are related to these network-state related patterns and NS interneuron subtypes, we assessed their preferred spiking phase during theta oscillations and their firing rate around SWRs^27,28,29,30. We assigned cells to putative NS interneuron subtypes using a multi-step process first assessing preferred theta firing phase, then firing patterns around SWR. To assess firing as a function of theta phase, spikes during theta periods (see the ‘Preprocessing of LFPs and detection of sharp-wave ripples and theta periods’ section) for each cell were sorted into 18° theta phase bins, including all theta cycles. For each potential NS interneuron subtype, we performed a one-tailed t-test to compare the raw spike counts between that subtype’s preferred phase (203–339° for PV-expressing basket cells (PVBCs), 130–240° for axo-axonic cells (AACs), 74–236° for cholecystokinin-expressing (CCK) cells and 347–171° for bistratified cells) and the non-preferred phases. Cells with a false-discovery rate (FDR)-corrected P < 0.05, indicating strong preferred theta phase within one or more of the tested subtypes, were sorted by their t-scores for each subtype. For each cell, if the top t-score was more than 0.5 above the next highest t-score, the cell was assigned the single subtype associated with the top t-score. If any of the top three t-scores were within 0.5 of each other, then a cell was assigned multiple subtypes associated with the highest t-scores. The theta-phase assignment was then curated by firing rate around SWRs. For each cell, we assessed the firing patterns as a function of binned time periods during and around SWRs, comparing the spike counts around the SWRs to shuffled non-theta, non-SWR baseline periods, as described previously²⁸. As the SWRs are asymmetrical, we normalized the time around the SWR as follows: the period between the start and middle of the ripple was divided into four bins, and the same bin size was used for the pre-ripple period. Similarly, the period between the middle and end of the ripple was divided into four bins, and the same bin size was used for the post-ripple period. For comparison, we randomly selected 100 non-theta, non-SWR periods baseline periods of the same length as the SWRs. A cell was classified as a PVBC or a bistratified cell if spiking was elevated during SWRs, specifically the spike counts in six bins around the middle of the ripple were higher than the mean + 2 s.d. of the baseline. If a cell exhibited a biphasic pattern, meaning that its spike counts in the four bins around the ripple start was higher than the mean + 1 s.d. of the baseline, and the spike counts in ten following bins was lower than the mean − 2 s.d. of the baseline, then this cell was classified as AAC. As a previous study showed that CCK cells have little change in firing rate during the SWRs³⁰, we assigned CCK to the cell if the spike counts in four bins around the ripple start, and four bins around the ripple end, were both within the range of mean ± 2 s.d. of the baseline. For cells with multiple subtype assignments based on theta phase, if their theta-assigned subtypes overlapped with the SWR-assigned subtypes, then the overlapping subtype was the final subtype assignment. On the basis of these criteria, we identified 137 out of 203 NS interneurons with a single subtype assignment, among which there were 41 AACs, 21 PVBCs, 27 bistratified cells and 48 CCK cells.

Place-field analyses

The occupancy-normalized firing rate map of putative pyramidal cells was quantified from spike counts and time spent in 5° position bins each smoothed with a Gaussian kernel (s.d. = 2 bins), excluding periods of stillness (movement speed <2° s⁻¹). The rate map was constructed by dividing the smoothed spike count by the smoothed occupancy for each bin. The following criteria were used to identify place cells among putative pyramidal cells: (1) mean firing rate of less than 10 Hz to exclude potential interneurons; (2) peak firing rate of at least 1 Hz; and (3) spatial information content greater than the 95th percentile of the information content generated from shuffled (repeated 1,000 times) data. Spatial information, expressed in bits per spike, was computed using the formula⁶⁵:

where p_i is the probability of the animal occupying the position bin i, λ_i is the mean firing rate of the cell in bin i and λ is the mean firing rate across all position bins. Goal-representing cells (goal cells) were pyramidal cells that had a place field peak in the AZ or RZ. Non-goal representing cells (non-goal cells) were defined as pyramidal cells without a place field peak within 20° (2 zones) of the start of the RZ. The field stability of goal or non-goal cells was measured using the Pearson correlation coefficient of trial-by-trial rate map correlations.

Multiple linear regression

To control for the well-documented relationship between movement speed and interneuron activity, we used multiple linear regression. We also accounted for potential effects of position-specific lick rates on firing activity. For each unit, we fit a multiple linear regression model with position-binned trial-by-trial firing rates as the response and position-binned speed, lick rate, and the interaction between speed and lick rate as predictors. We then subtracted the expected effects of speed and lick behaviour from the observed firing rates. The remaining data (residuals) were used in further analyses as estimated neural activity that could not be attributed to position-related changes in speed or lick rate across trials. For visualizing population activity, we first normalized residual firing rates over the binned position by dividing each bin by the peak firing rate per unit and averaged rewarded trials per unit. Thus, the normalized firing was scaled from 0 to 1 with 1 being the peak residual firing of each cell. To illustrate the change in residual firing activity from the baseline, we subtracted the baseline firing rate defined as the mean normalized firing rate of the first two bins (in the position range of [−60, −50]) degrees where zero refers to the start of the RZ. The resulting change in normalized firing is a fractional change (or percentage change) and was shown as the mean and s.e.m. averaged over cells or shown per cell. In heat maps, we then sorted units based on the binned position with the peak or trough activity, for pyramidal cells or interneurons, respectively. We also tested other nonlinear regression approaches and found that the linear regression performed similarly to or better than other methods (Supplementary Table 4).

Quantifying firing activity around goal locations

To quantify the proportion of units with significantly increased or decreased activity in the familiar environment, we first created an occupancy normalized firing rate map (as described above) using a 2° bin size for each RZ-centred trial (from −60° to 70° with zero being the start of the RZ) per unit. We then used a generalized linear model to find the best linear fit for the rate map over the pre-RZ position bins (−60° to 0°) and obtain a P value and estimated coefficient (slope) per unit. Only units with significant adjusted P values after correcting for the FDR of 0.01 were identified as units with significant activity change. This approach was applied to both pyramidal cells and interneurons to find significant changes in firing around goals. On the basis of our observation of decreased activity on average in interneurons and increased activity on average in pyramidal cells around goals, we aimed to identify interneurons with significant decreases in activity and pyramidal cells with significantly increased activity around goals. We included interneurons with significant negative coefficients as interneurons with significantly reduced activity and we included pyramidal cells with significant positive coefficients as pyramidal cells with significantly increased activity.

The firing rate changes around the new RZs in the novel environment tended to be more variable than in the familiar environment. We therefore chose a different approach to identify units with a significant increase or decrease in firing in the novel environment to average over in Fig. 3b. We randomly shuffled both the position-binned trial-by-trial maps of firing rates, movement speed and lick rates used for multiple linear regression. This process was repeated 1,000 times for each unit to generate a shuffled distribution. We compared these shuffled distributions in each position bin against the observed session-averaged residual firing rate in the same position bin. We identified units with a significant decrease or increase at each bin if the observed residual was either less than the 10th percentile (for interneurons) or greater than 90th percentile (for pyramidal cells), respectively, of the shuffled distribution at each position bin. The population averages (Fig. 3b) are the average of units that had at least one bin determined to be significant 10° before and after the RZ. We indicated the first bin within −40° of the RZ with a persistent decrease in firing, meaning that firing decreased below the baseline and stayed below the baseline until the RZ (Fig. 3b (triangles)). The persistent decrease in firing on day 1 started at −45°.

We assessed how goal-selective inhibitory decreases develop within the first day of exposure to the first novel environment. On this first day, animals have already learned the parameters of the VR environment and task from the familiar environment, and now must learn where to lick for reward in a new environment for the first time. We analysed interneuron firing over blocks of 25 trials as animals learned the novel track. ROC curves were generated for the same trial blocks using pooled speeds in the AZ and NRZ across 7 WT animals. The trial-level speeds were min–max normalized per day and aggregated across animals for group-level visualization of the first and last trial blocks.

Ripple content decoding

To control for animal position and position-related variability in behaviour, we included only SWRs that occurred while the animal was in the AZ or RZ in this analysis. To determine the content of individual ripple events, we performed sequenceless decoding to decode each ripple as a single time window⁶⁶. Before the decoding position during ripples, we confirmed decoding of current position during running in the familiar environment as this neural activity would be expected to represent current position. For each ripple, we calculated the spatial probability distribution using a simple Bayesian decoder as previously described^57,66. In brief, the probability of particular positions given the spiking activity at each timepoint (expressed in n_PositionBins × n_Time) was calculated using the formula:

where P(X|\(\bfN_1^C\)) is the probability of position X (distances relative to the RZ using 5° bins) given \(\bfN_1^C\), a vector of spike counts for all C cells recorded simultaneously within the specified time window. For all ripple events, we used a single 250-ms time window centred at the midpoint of each event regardless of its duration, and the decoder was applied to spiking within this window. P(N_i|X), the probability that cell i fires N_i spikes at position X, was computed using the population firing rate map averaged across trials (a n_Units × n_Bins matrix using 5° position bins as a function of distance to RZ, from −60 to 70°) multiplied by the decoding time window. P(X|\(\bfN_1^C\)) was then normalized across position bins to sum to 1. From the single probability estimate, we identified the decoded position bin with the highest spatial probability as the most likely spatial information (expressed as the relative distance to RZ) carried by the population activity during each event.

Theta modulation of firing

Theta modulation was analysed during running periods when the movement speed was greater than 2° s⁻¹ in the AZ. For each cell, the theta phase of spikes occurring in the defined running periods was extracted. The preferred theta phase was calculated as the circular mean of the theta phases for the spikes. The vector strength was calculated for each cell by implementing the ‘circ_r’ function from the ‘Circular Statistics Toolbox (Directional Statistics)’ in MATLAB (v.R2023a).

Immunohistochemistry

We used an additional six PVxAi32 mice (3 females) to verify the expression of ChR2 localized in PV-expressing interneurons. Thirty-micrometre coronal sections were blocked in 5% goat serum in 1× PBS for 30 min followed by 30 min in 5% goat serum with 0.3% Triton X-100. After blocking, the sections were incubated in primary antibody rabbit anti-parvalbumin (Swant, PV27, 1:5,000) at 4 °C overnight, washed in 1× PBS three times for 5 min each, incubated with secondary antibody goat anti-rabbit IgG Alexa Fluor Plus 647 (Invitrogen, A55055, 1:2,000) at room temperature for 1 h and washed three times in 1× PBS. The sections were mounted and imaged at ×10 or ×20 with an LSM 700 laser-scanning confocal microscope (Zeiss). Images were analysed using Zen Blue (v.3.3) microscopy software.

Statistical analysis

For data with repeated samples from the same animal and day, we used LMM analysis in R (v.4.2.2) and lme4 package⁶⁷ (v.1.1.35.1) to evaluate significant differences while controlling for repeated measures from sessions or animals. This approach was used for most analyses including data from multiple cells recorded from the same animal on the same day. Statistically significant differences were first estimated with an ANOVA with Kenward–Roger’s methods using the lmerTest package (v.3.1.3) with F-statistics reported⁶⁸. The emmeans package (v.1.8.9; https://cran.r-project.org/web/packages/emmeans/index.html) was used to adjust P values for multiple comparisons. For pairwise comparisons, we assessed significant differences using estimated marginal means and reported Tukey-adjusted P values and T-ratios (indicating β/s.e.(β), where β is the regression coefficient). To determine statistically significant learning over days in WT mice, we included the areas under the behavioural ROC curves as the dependent variable; day, environment and day by environment interaction terms as fixed effects; and animal IDs as a random effect. Thus, the model specification for WT mice was as follows: AUC ~ day + environment + day × environment + (1|AnimalID). For PVxAi32 mice, our main comparison was between goal stimulation and sham stimulation conditions that occurred in the novel environment only; we therefore included AUC as the dependent variable; day, stimulation condition (not environment) and the interaction between the two as fixed effects; and animal ID as a random effect. Thus, for PVxAi32 mice, we used the following model specification: AUC ~ day + stimulation condition + day × stimulation condition + (1|AnimalID). Comparison of spatial firing (including spatial information, rate-map correlation, effects of position and temporal bins, theta modulation, peak firing rate) between groups were compared using the following model specification: for WT mice, spatial information ~ day × environment + (1|AnimalID/CellID); for PVxAi32 mice with goal and sham stimulation comparisons, spatial information ~ day × stimulation_condition + (1|AnimalID/CellID). To show significant interaction effects, asterisks are indicated between novel days 1–3 and familiar days 1–3 or sham stimulus days 1–3 and goal stimulus days 1–3 in the figures.

For data that were sampled per session, we tested for statistically significant differences using a nonparametric two-sided Wilcoxon rank-sum test for non-uniformly distributed data. This approach applied to things like the proportion of ripples with near versus far goal content, which was computed per day and normalized within animal. Note that P < 2.2 × 10⁻¹⁶ indicates that the computed P value is below the minimum possible value reported by R. Similarly P < 0.001 indicates that the P value is the minimum possible value for tests that control for multiple comparisons.

For nonparametric paired comparisons, we used Wilcoxon signed-rank tests with the Bonferroni method to correct for multiple corrections. To identify position or time bins with firing rate changes significantly different from zero, we used one-sample permutation t-tests (5,000 times) and indicated these with colour coded horizontal bars above plots of cell-averaged firing as a function of position or time.

Data with error bars were reported as mean ± s.e.m. Details on the statistical analyses for each figure panel are reported in Supplementary Tables 5–22.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.