Systematic review
We conducted a systematic review of population-based studies to investigate changes in incidence and prevalence of CD and UC across global regions over time. The systematic review was conducted in accordance with the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) 2020 statement51.
Search strategy
We reassessed population-based studies reporting the incidence and prevalence of IBD from our team’s two previous systematic reviews3,4, covering the period before 2017. We updated the previous systematic reviews by performing a search of Embase, MEDLINE, PubMed and Web of Science for the period covering 1 January 2017 to 8 May 2024 with no language restrictions (the search strategy is shown in Supplementary Table 3).
Study selection
All studies underwent independent title and abstract screening by at least two reviewers. The reference lists were also inspected for additional citations. We included population-based studies published in article form at any time or abstracts from 2020 or later, which reported the incidence and/or prevalence of CD and/or UC separately or provided sufficient information to calculate the corresponding incidence or prevalence. Population-based studies were defined as studies deriving incidence and/or prevalence for the entire population of a specified geographical region or a representative sample. Exclusion criteria were as follows: no defined geographical region, less than 1 year of data, study population limited to paediatric cases only, self-reported cases identified by survey, reviews and clinical trials. Studies published in languages other than English were translated using Google Translate52. All included articles were re-evaluated by authors with local expertise and local language proficiency (see the ‘Data verification’ section below).
Data extraction
Author, publication date, geographical area (region and/or subregion), study period, ages, year (or midpoint of range), total population, data type (incidence or prevalence), rate type (crude or standardized), rate of UC, CD and/or IBD-unclassified (IBD-u) and case counts were extracted from each selected study. Aggregate rates were removed if an annual rate for the mid-period year was available. Missing population values were pulled from publicly available official statistical records53,54,55,56,57,58,59,60,61. For incidence data, we calculated the summed population for the time period; for prevalence data, we recorded the population at a given timepoint or used the mid-period population in cases of period prevalence. Data extraction and verification were conducted by at least two reviewers. In cases of disagreement between reviewers, consensus was reached through discussion.
Quality assessment
The quality of each study was independently assessed by two reviewers using a modified Joanna Briggs Institute Checklist for Prevalence Studies62. An additional quality measure was included to identify studies that were strictly population-based (that is, those that identified the entire population sample). Studies that used a representative sample or may have missed some cases due to the sampling method were of lower quality. The results of the quality assessment are presented in Supplementary Table 4.
Data verification
All steps of the systematic review (abstract review, full-text review, data extraction, quality assessment) were conducted by at least two members of a trained centralized team at the University of Calgary to ensure methodological consistency. Additional data verification occurred through international partners from the International Organization for the study of IBD (IOIBD) and the Global IBD Visualization of Epidemiology Studies in the 21st Century (GIVES-21) consortium. Experts from IOIBD and GIVES-21 confirmed the inclusion of studies, verified data accuracy and suggested additional studies that may have been missed (Supplementary Fig. 1). They confirmed the population-based status of the studies, addressed conflicts in language translation and provided local context (for example, study quality), including explanations for outlier results.
Rate calculation
Crude incidence or prevalence was calculated from case counts and the population of the catchment area. If case counts were not provided or the population of the catchment area was not available, we used the rates reported in the papers, whether presented in text, tables or extracted from plots using OriginPro63 or juicr64.
Temporal data analysis
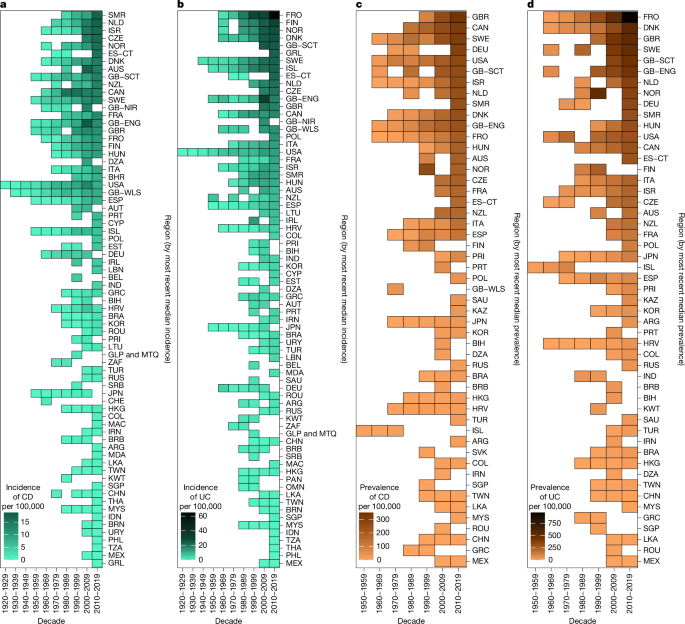
When multiple studies overlapped in region and time, we averaged rates to create a single value for that region and year. Data preprocessing for analysis and visualization of decade-level rates involved weighting the mean rates calculated by region for each year according to the population of that area for that year. Weighted rates were aggregated by decade. This weighting method enabled us to combine regional and subregional data to generate a single value for a region in a particular decade. Aggregated subregional data were treated as representative for a region when no other regional data were available. Missing case counts were back-calculated from provided per 100,000 values and populations. In rare cases in which the catchment area population values were not available, non-weighted means were used in the aggregation. When IBD-u was reported separately, it was combined with UC.
Temporal trends for studies and regions that reported at least three datapoints within a 5-year period were established using Poisson regression (or, if overdispersed, negative binomial regression) models built in R65, with the year as the sole predictor variable and the incidence rate of either CD or UC as the outcome. We determined the average annual percentage change with associated 95% CI for incidence by exponentiating the β coefficients from the regression models (Supplementary Table 1).
Machine-learning classification
Exploratory data analysis
We visually inspected scatterplots of historical trends in incidence and prevalence for early industrialized, newly industrialized and emerging regions to determine epidemiologic stages for a subset of regions with data extracted during the systematic review. On the basis of the assumption that Canada, the United States, most of western Europe, Australia and New Zealand are currently in stage 3, we assigned stage classifications to approximately 65% of our dataset (Supplementary Fig. 16).
k-nearest-neighbors-assisted labelled dataset creation
As regions and subregions do not transition between stages simultaneously, we built a k-NN classification algorithm to support manual data labelling. The k-NN algorithm facilitated an iterative labelling process by classifying regions with robust historical incidence or prevalence data into one of three classifications: stage 1, stage 2 or stage 3. Owing to skewed class proportions (that is, scarcity of stage 1 data) and missing values within classes, we developed four separate models: incidence of CD, incidence of UC, prevalence of CD and prevalence of UC. Each model used two features: incidence or prevalence and the absolute difference in incidence or prevalence from the previously available year of data.
A 75/25 train/test split (n = 1,581/n = 527) was applied. The value of k-neighbours was set to the square root of the number of instances in the training data and adjusted accordingly for each model. A Monte Carlo simulation with 1,000 sampling loops was run for each model. The model accuracy (Supplementary Table 5) was determined using the following formula:
$${\rm{acc}}( \% )=100\times \left(\frac{M}{L}\right)$$
(1)
where M equals the number of misclassifications (that is, instances in which the model’s classification output differed from our manual classification) and L equals the number of Monte Carlo sampling loops. Three iterations were performed in which the k-NN model output was inspected with successive relabelling of the input data, achieved through consensus among three analysts. At each iteration, additional regions and subregions were added to the labelled dataset until approximately 80% of our total dataset was labelled, with the intention of using it for training and validating a random-forest classifier.
Random-forest classifier
A random-forest classifier was built in R65 using the randomForest66 package. Random forests use an ensemble learning method, in which a specified number of decision trees is generated, and the results are aggregated. The class selected by the model most frequently becomes the resulting classification18. Each individual decision tree determines a class prediction based on a random subset of features, which reduces the likelihood of overfitting and improves the accuracy of class prediction67. Random-forest classifiers do not require data scaling and are robust to outliers and noise, which is essential given the heterogeneity and imbalance in our dataset and the complexity of analysing systematic review data.
Features and data imputation
Classifying a region’s stage in a particular year was based on 16 possible features: (1) CD incidence; (2) UC incidence; (3) CD prevalence; (4) UC prevalence; (5) rates of change for incidence of CD; (6) rates of change for incidence of UC; (7) rates of change for prevalence of CD; (8) rates of change for prevalence of UC; and (9–16) indicators of imputed values for each of the preceding eight variables. The structure of the classifier required a value to be specified for each of the above features for each year of available data by region.
Imputation was used to ensure that a value was specified for each of the primary eight features. Imputation was conducted within a single region across all available datapoints for that region. When at least two datapoints were available for a region, linear interpolation was used, using the next observation carried backward and the last observation carried forward to extrapolate missing values outside the available interval. In cases in which only a single datapoint was available for a region, that value was extrapolated to all missing data for that region. Zero imputation was applied to the remaining missing datapoints. Features 5–8 were included to account for the potential increase or decrease in incidence and prevalence over time. As classifications were made by the random-forest model at the level of the region and year, and many regions lacked incidence or prevalence values for certain years, features 9–16 were included so the random-forest classifier could account for unavailable data that were imputed for classification purposes.
Random-forest models provide a measure of feature importance, allowing for an examination of which data types (incidence or prevalence) and which disease types (CD or UC) contributed most to the classifications across the three stages (Supplementary Fig. 20).
Training, validation and model architecture
The random-forest model was trained using a subset of data from the labelled dataset (n = 1,647). Training and validation sets were created using a 75/25 split (n = 1,235/n = 412) of the labelled dataset, with the out-of-bag (OOB) error estimate used to tune model hyperparameters: ntree (number of trees aggregated) and mtry (number of features used at each split in the tree). The model with the smallest OOB error estimate (OOB = 4.86%) used ntree = 1,000 and mtry = 5 (out of 16 possible features). The random-forest’s classification accuracy on the unseen validation data was 95.15% (95% CI = 92.60–97.01); this means that the random forest correctly classified a region-year as stage 1, stage 2 or stage 3 approximately 95% of the time, indicating an appropriate model fit and performance (Supplementary Table 6).
Random-forest output
The output from the random-forest model was used to assign an epidemiologic stage to regions with limited incidence and prevalence data (n = 842), resulting in a complete dataset with stage classifications for all regions in the dataset across time (n = 2,489). As classifications were based on a single year of data, a decade-level stage classification for a region was calculated by identifying the mode class label from the random-forest model output for years within a decade. In cases in which the model provided an even split of stage classifications for a region within a decade (n = 2: Poland, 2010s; China, 2020s), four expert reviewers assessed available incidence and prevalence data and manually assigned a stage classification for that decade. When no regional data were available, the stage classification for a region was determined based solely on subregional data.
Coalescing ranges
The distribution of incidence and prevalence data for each stage was derived from the machine-learning models and used to calculate CRs, defined by the 25th and 75th percentiles. Negative binomial regression models followed by post hoc comparisons of estimated marginal means using the emmeans68 package in R with Tukey adjustment for multiple comparisons were used to evaluate significant differences in CR between stage 1, stage 2 and stage 3 in each of the following: CD incidence, UC incidence, CD prevalence and UC prevalence.
Ulcerative colitis/Crohn’s disease ratio
To calculate the UC:CD ratio, the annual population-weighted mean UC incidence was divided by the annual population-weighted mean CD incidence and assigned an epidemiologic stage on the basis of the output of the machine-learning model. The association between UC:CD ratio and epidemiologic stage was modelled using negative binomial regression. Pairwise comparisons between the stages were performed using the emmeans68 library in R, with estimated marginal means using Tukey adjustment for multiple comparisons.
Societal indicators
Five societal indicators were examined in relationship to epidemiologic stages: the AHDI, obesity rate, percentage urbanization, the Universal Health Coverage Service Coverage Index (UHC) and the WDI. AHDI is an index score (0–1) that captures the geometric mean of normalized life expectancy, mean years of education, gross domestic product (GDP) per capita and Varieties of Democracy’s Liberal Democracy Index20. AHDI is available in 5-year increments, for which we performed inner-linear interpolation to achieve annual measures. Obesity data were extracted from the WHO database, providing a measure of the percentage of an adult population with a BMI > 30 kg m−2 (ref. 69). Percentage urbanization data were extracted from a United Nations database, providing a measure of the mid-year percentage of a population living in an urban setting70. UHC is an index score (0–100) that quantifies various aspects of healthcare, including reproductive health (for example, the percentage of pregnant people with ≥4 prenatal care visits), prevention of communicable diseases (for example, the percentage of 1-year-old children with adequate diphtheria, tetanus and pertussis vaccination), non-communicable diseases (for example, the percentage of cervical cancer screening in women aged 30–49 years) and healthcare access (for example, the number of hospital beds per capita)22. The UHC is also available in 5-year increments, for which we performed an inner-linear interpolation to achieve annual measures. WDI is an index score (0–1) calculated by dividing the available calories per person per day from animal oils and fats, milk, eggs, plant oils and fats, and sugars by the total available calories per person per day, similar to the methodology provided by Azzam in 2021, extended to all regions within our dataset24. Regional calorie availability was extracted from the Food Balance sheets published by the Food and Agriculture Organization71.
Time- and region-specific values from each of these five indicators were stratified by the three epidemiologic stages (as derived by the machine-learning classifier) and statistically compared across stages using Kruskal–Wallis nonparametric tests with post hoc comparisons using Wilcoxon rank-sum tests with adjustment for multiple comparisons.
Modelling stage 4 using PDEs
To explore the potential growth characteristics of IBD prevalence in stage 3 regions, we modelled the time-dependent prevalence using historic prevalence and incidence data, plus population projections from Canada, Denmark and Scotland (Lothian). Calculations were completed using Mathematica (v.13.1)72.
Data sources
Incidence and prevalence of IBD were calculated for Canada, Denmark and Scotland (Lothian) from administrative data provided by each region (Supplementary Table 7).
For Canada, population-based provincial administrative healthcare data were combined from Alberta, British Colombia, Manitoba, Newfoundland and Labrador, Nova Scotia, Ontario, Quebec and Saskatchewan to capture data for 2007–201415. In Denmark, nationwide individual-level healthcare information was obtained from the Danish National Patient Register for 2010–2017 (ref. 73). For Scotland, data for the Lothian region (Edinburgh and surrounding area) were sourced from TrakCare (InterSystems) electronic health records for 2010–201713. Projections of the population age-distribution for 2018–2043 were gathered from Statistics Canada26,53, Denmark27,74 and Scotland (Lothian)28,70 (Supplementary Fig. 21).
Region-specific data transformations
Raw historic prevalence, incidence and population data for Canada, Denmark and Scotland (Lothian) were transformed. All age categories (<10 years, 10–17, 18–24, 25–34, 35–44, 45–54, 55–64, 64–79, 80+) were closed, with an upper and lower bound, except for the highest age category (80+), for which the centre of the age bin was set to the estimated population-averaged mean value (86 years for 80+, 93 years for 90+ and 106 years for 105+). The prevalence up to age 110 was estimated using linear extrapolation, constrained to have a zero or negative slope, and to be equal to or greater than zero, while the historic incidence and population projections were set to zero at age 110.
Deriving the equation
The change in prevalence over time was modelled using a PDE75,76 that has previously been used to estimate the future prevalence of chronic diseases, including diabetes mellitus77,78 and dementia25. The PDE is derived from a compartment model75,76 (Supplementary Fig. 22) and has widespread applicability to diseases where the incidence rate is known or can be modelled.
The prevalence of a disease p depends on both time t and the age distribution of the disease cohort a. The change in prevalence as a function of both time and age is modelled by equation (2)25:
$$\frac{\partial p}{\partial t}+\frac{\partial p}{\partial a}=(1-p)\left[i-m\frac{p(R-1)}{p(R-1)+1}\right]-r\,p+\mu $$
(2)
Here, \(\frac{\partial p}{\partial t}\) and \(\frac{\partial p}{\partial a}\) are the partial derivatives of prevalence with respect to time and age. The incidence rate i, full population mortality rate m, relative mortality ratio R (ratio of those with the disease to those without) and recovery rate r are all functions of both time and age. The migration term μ is a function of time, age and prevalence.
Simplifying the equation
For parsimony, we neglect terms in equation (2) that are not applicable or are small enough to be ignored. IBD is a chronic, incurable disease and we therefore ignored the recovery rate, r. The mortality term, m p(R − 1)/[p(R – 1) + 1] was set to zero owing to the relatively small difference in life expectancy between those living with IBD and the general population79. Similarly, the migration term, μ, was set to zero because immigration to the regions being examined greatly exceeds the emigration80,81,82, and the prevalence of IBD is lower in new immigrants than in the existing population83,84. Omitting these three terms yields the simplified equation
$$\frac{\partial p}{\partial t}+\frac{\partial p}{\partial a}=(1-p)i(t,a)$$
(3)
which makes explicit the age and time dependence of the incidence.
Solving the equation
Given the age distribution of prevalence at an initial time, p0(a), and assuming that the prevalence must be zero at age zero, equation (3) is solved using the method of characteristics85 to yield
$$p(t,a)=\left\{\begin{array}{c}\begin{array}{cc}1-[1-{p}_{0}(a-t)]{{\rm{e}}}^{-{\int }_{0}^{t}i(x,x+t-a){\rm{d}}x}, & 0\le t < a\\ 1-{{\rm{e}}}^{-{\int }_{0}^{a}i(x+a-t,x){\rm{d}}x}, & 0\le a < t\end{array}\,\\ \,\end{array}\right.$$
(4)
To calculate prevalence as a function of time, we multiply by the normalized population age-distribution σ(a) and integrate over age, such that
$$p(t)={\int }_{0}^{\infty }p(t,a)\sigma (a){da}$$
(5)
Equation (5) allows us to extrapolate the prevalence of IBD over the coming decades. To do so, three additional pieces of information are required: the initial prevalence of IBD as a function of age, the incidence rate of IBD as a function of age and time, and projections of the population age distribution.
Age-dependent IBD incidence and prevalence
A linear interpolation of the age-dependent IBD prevalence data for Canada (2014), Denmark (2017) and Scotland (2017) served as the initial prevalence, p0(a), for modelling (Supplementary Fig. 23). Data for IBD incidence during 2007–2014 for Canada and 2010–2017 for Denmark and Scotland were compiled (Supplementary Fig. 24), with the average incidence from these 8 years serving as the age-dependent component of the model incidence rate, f(a). A time-dependent component was added to the incidence, modelled as an exponential growth process with growth rate g:
$$i(t,a)=f(a){{\rm{e}}}^{t\times {\rm{l}}{\rm{n}}(g)}$$
(6)
Model verification
To verify that our model describes the prevalence of IBD, we compared the model’s output to historical data, specifically the age-structured prevalence from 2014 for Canada and 2017 for Denmark and Scotland. Starting with equation (4), p0(a) was taken as the age-structured prevalence from 2002 (Canada), 2010 (Denmark) and 2009 (Scotland), and a time-independent incidence rate f(a) as the average over the years 2007–2014 (Canada) or 2010–2017 (Denmark and Scotland) (Supplementary Figs. 23 and 24). For Canada, the model produced a 2014 prevalence of 0.65%, compared with the observed 0.65% (Supplementary Fig. 25a). For Denmark, the model produced a 2017 prevalence of 0.98%, compared with the observed 0.94% (Supplementary Fig. 25b). For Scotland, the model produced a 2017 prevalence of 0.88%, compared with the observed 0.79% (Supplementary Fig. 25c). The high degree of concordance suggests that the simplified model is reasonably accurate for longer-term modelling of general prevalence trends.
Slopes and central difference approximations
Central difference approximations to the slope of the time-dependent IBD prevalences in Canada, Denmark, and Scotland were calculated to determine the percent change in prevalence for each year of data. The central difference approximations is calculated by:
$$\delta p(x)=\,\frac{p(t+h)-p(t-h)}{2h}$$
(7)
where p(t) is the prevalence at year t, and h is the time-step, set equal to 1 year (that is, the frequency with which the time-dependent prevalence was calculated). Central difference approximations were averaged over 5-year periods to determine whether Canada, Denmark or Scotland had reached prevalence equilibrium by 2043.
Yearly incidence change scenarios
We selected five values of the growth constant g in equation (6): 0.98, 0.99, 1.00, 1.01 and 1.02, corresponding to 2% and 1% incidence rate decreases per year, no change, and 1% and 2% incidence growth per year, respectively. To model current trends, we assume that the incidence rate is constant, as per the 2007–2014 (Canada) and 2010–2017 (Denmark and Scotland) observed data, until 2024 at which time the exponential increases or decreases in incidence begin.
Strengths and limitations
This study represents, to our knowledge, the most comprehensive summation of population-based data on the incidence and prevalence of IBD, spanning a century of historical data that was used to explore spatial and temporal epidemiologic patterns across the world. We used a unique machine-learning approach to classify regions into three epidemiologic stages over time and established benchmarks to define incidence and prevalence ranges for each stage. Furthermore, to our knowledge, this is the first study to model the transition to a theoretical fourth stage, where prevalence growth plateaus due to an ageing IBD population and stable incidence rates. However, the interpretation of our findings should be evaluated in the context of inherent limitations.
We relied on incidence and prevalence data that varied in quality. Historical data from the twentieth century, regions lacking healthcare surveillance systems and fractionated healthcare systems that impair population-based case capture were of lower quality, leading to heterogeneity in the reported data. To address this, we conducted a quality assessment of each paper through a centralized evaluation process, which was further complemented by assessment from regional experts. Regions with administrative healthcare databases can electronically capture IBD cases using coding algorithms (for example, ICD coding); however, validation studies have demonstrated misclassification errors that lead to the inclusion of false positives, potentially inflating incidence and prevalence. By contrast, regions without population-based electronic healthcare surveillance systems relied on medical registries to identify IBD cases. While this approach results in highly accurate diagnoses, it may miss cases (for example, milder cases not followed by gastroenterologists), potentially leading to underestimation of incidence and prevalence.
The primary source of inconsistency in our random-forest model arises from the availability epidemiologic data, leading to an imbalance across stage classes. The scarcity of data from emerging regions and historical data from the earlier part of the twentieth century resulted in fewer studies available to assess stage 1. Moreover, data from stage 1 regions, which are predominantly low-income, often lacked electronic surveillance systems to support case identification. Consequently, we allowed case-ascertainment approaches that may have missed IBD cases such as surveying gastroenterology offices or hospital-based capture systems, provided that the hospitals serve a defined catchment area. However, in our quality assessment, we differentiated population-based studies that met our strict definition (that is, complete capture of cases in a defined region) from those that did not (that is, a representative sample). Our repository (https://kaplan-gi.shinyapps.io/GIVES21/) allows users to subset data by these two categories of population based.
Regional data are missing or limited in many highly populated areas in Africa, Asia and Latin America. Our machine-learning classifier was trained on robust data, enabling us to reliably classify regions during different time periods when data are scarce. Moreover, our GIVES-21 consortium is currently conducting high-quality, population-based epidemiologic research in over 30 regions with limited IBD data from newly industrialized and emerging regions33. Our repository (https://kaplan-gi.shinyapps.io/GIVES21/) is being continuously updated to allow for integration and reanalyses of global epidemiologic data as new information is available. To capture the most recent population-based data available, data from 2020–2024 were included as a partial decade in our analyses. Although this period does not provide a complete decade for stratifying stage classification, its inclusion highlights the best estimate of the current burden of IBD in regions where these years of data are available.
While the model was highly accurate (>95%) in classifying regions into one of three stages, a few regions exhibited unexpected classifications: Ireland was classified as stage 2 during 2010–2019, which contrasts with other contemporary regions in Western Europe. Deviations between the model’s output and expected classifications were primarily observed in regions transitioning between stages, especially in cases in which there was a lack of comprehensive data or when subregional data were used in place of regional values. For example, Ireland’s classification for 2010–2019 was based on data from County Meath in 201086. These discrepancies highlight the need for more recent, population-based studies in such regions to improve the classification accuracy and refine estimates.
Our PDE models were developed with model parsimony in mind, and so did not include the differential mortality between the IBD and non-IBD populations; this implies that the projections serve as a likely upper bound on the future IBD prevalence. Furthermore, our classifier and PDE models did not directly account for immigration. Research shows that individuals immigrating from stage 1 or 2 regions to a stage 3 region eventually assume the IBD risk of their host region, particularly among the first-degree offspring83,84. Finally, we acknowledge that unexpected future events may influence future projections. For example, we varied incidence growth in the model within a range of +2% to −2% over a 20-year horizon; however, events that could result in a more substantial change in incidence (such as the discovery of an IBD cure, or a high-mortality pandemic) are not accounted for in our model. Moreover, we limited our analyses to three regions currently in stage 3 to predict the transition towards stage 4. Future research that includes data from other stage 3 regions are needed to ensure generalizability of these predictions.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.