Functional regimes define soil microbiome response to environmental change

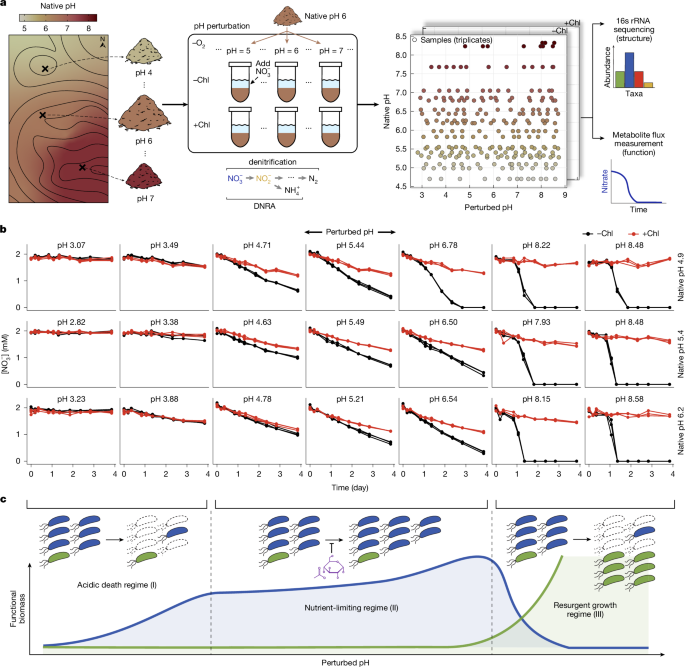
Sample collection, site description and soil characterization

Twenty topsoils were sampled across a range of pH values (4.7–8.32) from the Cook Agronomy Farm (Supplementary Table 1). The CAF (46.78° N, 117.09° W, 800 m above sea level) is a long-term agricultural research site located in Pullman, WA, USA. CAF was established in 1998 as part of the Long-Term Agroecosystem Research (LTAR) network supported by the US Department of Agriculture. Before being converted to an agricultural field, the site was zonal xeric grassland or steppe. CAF operates on a continuous dryland-crop rotation system comprising winter wheat and spring crops. CAF is located in the high rainfall zone of the Pacific Northwest region, and the soil type is classified as Mollisol (Naff, Thatuna and Palouse Series)⁶¹. Sampling occurred from 8 to 12 September 2022, post-harvest of spring crops, to reduce the impact of the plant on soil microbial communities. This period was during the dry season preceding the concentrated autumn rainfall.

Topsoils were collected from the eastern region of the CAF at a depth of 10–20 cm, other than Soil 1 and Soil 2 (depth of 0–10 cm). Eastern CAF practices ‘no tillage’, which eliminates soil inversion and mixing of the soil surface to 20 cm. The N fertilizer in this field has been primarily deep banded to depths of approximately 7–10 cm during the time of application, which creates a spike of nitrate resource in the soil depth we sampled. Each soil sample was obtained by cutting down through the hardened dry soil with a spade in a circular motion to create a cylindrical cake of soil of radius 10–20 cm until the desired depth. Each soil sample was not merged from sampling multiple replicates due to differences in pH in different locations. Samples were collected within a diameter of 500 m within the CAF to minimize the variation of edaphic factors other than pH. The large variation in soil pH comes from the long-term use of ammoniacal fertilizers and associated N transformations, which may undergo nitrification, resulting in the release of H ions. In combination, spatial pH variation increases with field-scale hydrologic processes that occur under continuous no tillage superimposed over a landscape that has experienced long-term soil erosion.

To maximize the coverage of sampled native pH, we used a portable pH meter (HI99121, Hanna Instruments) to directly measure and estimate the soil pH without having to make slurry on site to determine whether to sample the soil before sampling. For accurate pH values, pH was measured in the laboratory using a glass electrode in a 1:5 (soil to water w/w) suspension of soil in water (protocol of International organization for standardization (ISO) 10390:2021), where 7 g of soil was vortexed with 35 ml of Milli-Q filtered water, spun down, and filtered with 0.22 μm pore size. With these pH values, we selected 20 topsoil samples that are spread across a range of pH from 4.7–8.32 with intervals of 0.1–0.6. Twenty soil samples were sieved (<2 mm), removed of apparent roots and stones, and gravimetric water content was determined (105 °C, 24 h). The sieved samples were stored in the fridge for 0–3 months until the incubation experiment. For sequencing the initial community, subsamples were stored in −80 °C until the DNA extraction. The twenty soils were sent to the Research Analytical Laboratory (University of Minnesota, USA) to measure soil texture (soil particle analysis; sand, silt and clay composition), total carbon and nitrogen and cation exchange capacity. The soils were also sent to Brookside Laboratories for a standard soil analysis package (Standard Soil with Bray I phosphorus). Twenty soils had relatively similar edaphic properties: 5–9% gravimetric water content (g per g dry soil), soil texture of silty clay loam with 0% sand and 32–43% clay, and C:N ratio of 12–16 with 10–20 total carbon (mgC per g soil) (Supplementary Table 1).

To demonstrate the generality of our results from 20 CAF soils in other soils, we collected topsoil samples from 8 additional sites spanning natural preserves in IL (LaBagh Woods, Orland Grasslands, Moraine), IN (Pinhook Bog, Ambler Flatwoods) and the Sedgwick Reserve in CA (CL, EL and SCL grassland samples, managed by the University of California, Santa Barbara) in August 2024. Owing to the strong pH buffering capacity of the Orland, Moraine and SCL samples, we proceeded with five soils for which pH perturbations were feasible. Using the same methods as in the experiments conducted on the CAF soils (see below), we performed pH perturbation experiments, dynamic measurements of metabolites, and 16S rRNA sequencing. Of these, we analysed the metabolite dynamics of four soils (LaBagh, Pinhook, CLG13 and ELG13), as the Ambler soil had issues with nitrate retrieval under basic conditions during the Griess assay (for example, we could not reliably recover added nitrate using our extraction methods). Details of these soils and their characteristics are provided in Supplementary Table 1.

Soil rewetting, constructing soil pH titration curves and pH perturbation experiments

To mimic the autumn rainfall in the Pacific Northwest region and minimize the effect of spiking microbial activity by rewetting dry soils⁶², we rewetted the sieved soil for 2 weeks before the perturbation experiments at room temperature with sterile Milli-Q water at 40% of each soil’s water holding capacity. After resetting, a soil slurry was made by adding 2 mM sodium nitrate solution to the soil (2:1 w/w ratio of water to soil). The slurry was then transferred to 48-deep-well plates (2.35 ml of slurry per well) for incubation under anaerobic conditions (950 rpm, 30 °C) for 4 days. Anaerobic incubation was performed in a vinyl glove box (Coy Laboratory Products 7601-110/220) purged of oxygen with a 99%:1% N₂:CO₂ gas mixture, where the gaseous oxygen concentration was maintained below 50 ppm to prevent aerobic respiration⁵⁸.

To perturb the soil pH to desired levels, we constructed each soil’s pH titration curve for the 20 soils with varying native pH to know exactly how much acid or base to add to each soil sample. To do so, separate from the main pH perturbation experiment, we added 23 different levels of HCl (acid) or NaOH (base) in the slurry, final concentrations ranging from 0–100 mM HCl or NaOH. We colorimetrically measured the pH (see section below) immediately after and 4 days after adding each well’s designated amount of acid/base. Owing to natural soil’s buffering capacity, it takes 1–2 days to stabilize its pH level. Thus, we used the endpoint (after 4 days) pH measurements for all pH perturbations. We did a spline interpolation on the titration data points, plotting endpoint pH (y axis) against acid or base input (x axis), to compute how much HCl and NaOH needs to be added to the soil to obtain 13 different levels of pH with ~0.4 intervals ranging from pH 3 to 9, including the pH level without the addition of any acid or base. For Soil 19 and Soil 20, we had only 7 and 3 perturbed pH levels respectively, because the strong buffering capacity of these soils (native pH over 8) limited the range of pH perturbation. We additionally tested whether the anion of acid (Cl⁻) or the cation of base (Na⁺) had a distinctive effect on the nitrate reduction dynamics, which was not the case (for results, see Extended Data Fig. 2g and Supplementary Information, ‘Effect of base cation on nutrient release in soils’).

For the main pH perturbation experiment, the computed levels of concentrated HCl or NaOH were added to the slurry in the 48-deep-well plate with and without chloramphenicol treatment for each perturbed pH level in triplicate. The plates were immediately transferred to the shaking incubator (950 rpm in Fisherbrand Incubating Microplate Shakers 02-217-759, 3 mm orbital radius, 30 °C) inside the anaerobic glove box and incubated for 4 days. For chloramphenicol-treated samples, we added concentrated chloramphenicol solution to the slurry to obtain a final concentration of 1 g l⁻¹, after testing different doses to rule out the possibilities of unwanted growth due to chlormaphenicol resistance or degradation (Extended Data Fig. 2c and see Supplementary Information, ‘Effectiveness of chloramphenicol in preventing microbial growth in the soil’). To gauge the effect of the 2 mM nitrate, we had no-nitrate controls (0 mM nitrate) for both chloramphenicol-treated and untreated treatments in the unperturbed pH conditions. With antifungal cycloheximide controls (200 ppm) for all 20 soils, we confirmed that fungal activity minimally affects nitrate utilization dynamics (Extended Data Fig. 2a,b). We also confirmed that abiotic nitrate or nitrite reduction does not occur by measuring metabolic dynamics of autoclaved soil (120 °C, 99 min, autoclaved 5 times every 2 days; Extended Data Fig. 2d). To offset the effect of increasing metabolite concentration due to evaporation throughout the 4-day incubation period, we used the wells with just 2 mM nitrate, nitrite and ammonium solutions to correct for evaporation in the slurry samples for every time point. The values of the gravimetric water content of each soil were taken into account to correct for the dilution of 2 mM nitrate due to moisture in the soil. After the incubation, the plates were stored in −80 °C for sequencing endpoint communities.

Time-series slurry sampling, extraction, and colorimetric assays to measure nitrate, nitrite, ammonium, WSOC and pH

To obtain the metabolic dynamics, we subsampled 60 μl of the slurry into 96-well plates 10 times throughout 4 days (0, 4, 8, 19, 25, 31, 43, 55, 67 and 91 h), where the initial time point (T₀) is the time of pH perturbation and the start of anaerobic incubation. To measure nitrate and nitrite dynamics, extracts were prepared from the sampled slurries by adding and vortexing for 2 min with 90 μl of 3.33 M KCl solution (final concentration of 2 M KCl) and centrifuging at 4,000 rpm for 5 min. The supernatant was filtered at 0.22 μm with a vacuum manifold to remove soil particles that could interfere with colorimetric assays. Concentrations of nitrate and nitrite in the extracts were determined colorimetrically using the Griess assay⁶³ and vanadium (iii) chloride reduction method, following the protocol outlined previously⁵⁸. We confirmed that 95%–99% of the nitrate in the soil can be accurately retrieved and detected using this method, as verified by nitrate spike-in and extraction experiments in the soil. For all 20 CAF soils, the ammonium dynamics were measured colorimetrically using the salicylate–hypochlorite assay from the soil extracts⁶⁴. Chloramphenicol treatments in the samples led to consistent detection of 0.5 mM \(\rmNH_4^+\) due to its N-H moiety. The salicylate–hypochlorite assay is also affected by the amount of base (NaOH) in the samples, resulting in slightly lower detection of chloramphenicol in the chloramphenicol-treated samples (0.45 mM \(\rmNH_4^+\) in 100 mM NaOH perturbations). Taking advantage of these control measurements, we used the constant \(\rmNH_4^+\) levels in the controls without 2 mM \(\rmNO_3^-\) (no-nitrate controls) in the chloramphenicol-treated samples for each soil to offset the NaOH effect in the non-chloramphenicol samples and subtracted \(\rmNH_4^+\) levels caused by chloramphenicol in chloramphenicol-treated samples.

For WSOC measurements, we subsampled 60 μl of the slurry into 96-well plates at T₀ and endpoint (4 days). Then, soil extracts were prepared by adding, vortexing with 90 μl Milli-Q water, centrifuging at 4,000 rpm for 5 min, and 0.22 μm filtering the supernatant. Concentrations of the organic carbon in the supernatant were measured colorimetrically by the Walkley–Black assay, which uses dichromate in concentrated sulfuring acid for oxidative digestion⁶⁵. We subtracted 0.4 mgC ml⁻¹ from the chloramphenicol-treated samples because chloramphenicol gave rise to a measured value of 0.4 mgWSOC ml⁻¹ without additional carbon. For pH measurements, we subsampled 100 μl of the slurry into 96-well plates at T₀ and the endpoint. Then, soil extracts were prepared by adding, vortexing with 150 μl KCl solution (final concentration of 1 M KCl), centrifuging at 4,000 rpm for 5 min, and 0.22 μm filtering the supernatant. The pH of the 120 μl supernatant was determined colorimetrically by adding 4 ul of the multiple indicator dye mixture via the protocol described previously⁶⁶. The reason we used 1 M KCl method for pH measurement (ISO 10390:2021) was that, contrary to the KCl method, the H₂O method (using water instead of 1M KCl) resulted in a highly yellow colouration of the supernatants in strong basic perturbed samples, which interfered with the wavelength of the colorimetric pH assay. For samples of pH outside the range of the assay (below pH 3 and above pH 9), we used a pH micro-electrode (Orion 8220BNWP, Thermo Scientific). We calculated the endpoint perturbed pH as the average pH of the three biological replicate endpoint samples.

DNA extraction with internal standards, library preparation and 16S rRNA amplicon sequencing

We performed 16S amplicon sequencing on half of all samples: 10 (soils 3, 5, 6, 9, 11, 12, 14, 15, 16, 17; Supplementary Table 1) out of 20 soils were sequenced before perturbation and at the endpoint in both chloramphenicol-treated and untreated conditions, totalling 1,085 amplicon sequencing measurements. Genomic DNA was extracted from 500 μl aliquots in a combined chemical and mechanical procedure using the DNeasy 96 PowerSoil Pro Kit (Qiagen). Extraction was performed following the manufacturer’s protocol, and extracted DNA was stored at −20 °C. To estimate the absolute abundance of bacterial 16S rRNA amplicons, we added known quantities of genomic DNA (gDNA) extracted from Escherichia coli K-12 and Parabacteroides sp. TM425 (samples sourced from the Duchossois Family Institute Commensal Isolate Library, Chicago, IL, USA) to the slurry subsamples before DNA extraction. Equal concentrations of gDNA from these two strains were added. Both strains have identical rRNA copy numbers of 7 and comparable genome sizes of approximately 5,000 kb. DNA library preparation was performed using the 16S Metagenomic Sequencing Library Preparation protocol with a 2-stage PCR workflow (Illumina). The V3–V4 region was amplified using forward primer 341-b-S-17 (CCTACGGGNGGCWGCAG) and reverse primer 785-a-A-21 (GACTACHVGGGTATCTAATCC)⁶⁷. We confirmed using gel electrophoresis that the negative samples containing all reagents did not show visible bands after PCR amplification. Sequences were obtained on the Illumina MiSeq platform in a 2× 300-bp paired-end run using the MiSeq Reagent Kit v3 (Illumina) with 25% PhiX spike-ins. A standardized 10-strain gDNA mixture (MSA-1000, ATCC) was sequenced as well to serve as a positive control, which was confirmed to have relatively uniform read counts after assigning taxa.

Model and fitting

Consumer-resource model

Consider a consumer-resource model with one consumer variable (functional biomass x(t), biomass) and two resource variables (nitrate A(t) and carbon-nutrient C(t), mM), which evolves in time (t, day). The ordinary differential equations of the consumer-resource model can be expressed as:

The first two equations represent the resource consumption rates, which are determined by the functional biomass (x (g biomass)), the maximum consuming rates per unit biomass (r_A and r_C (mM per g biomass per day)), and the Monod functions (A/(A + K_A) and C/(C + K_C) (dimensionless)). Here we assume the affinities (K_A and K_C (mM)) to be fixed and small. So the Monod functions are 1 when A ≫ K_A or C ≫ K_C, and 0 when A→0 or C→0. The third equation represents the growth of functional biomass, which is determined by the maximum growth rate per biomass (γ (day⁻¹)) and the multiplication of two Monod terms indicating the fact that nitrate and carbon are non-substitutable (electron acceptor and donor, respectively). The growth is exponential (x(t) = x(0)e^γt) when both A ≫ K_A or C ≫ K_C, but growth stops when either A→0 or C→0. Therefore, in this model, the growth of biomass is limited by both resources, but the consumption of one resource can continue when the other resource runs out and the biomass growth stops. For example, we believe this happens when C→0 in Regime II and the consumption of A continues (Fig. 2). For a discussion of models that consider multiple biomasses and carbon sources, see Supplementary Information ‘Justifying the effective 1-biomass model despite the diversity of denitrifying taxa’.

Solution for nitrate dynamics

To find the solution for nitrate dynamics, we rescale the equations by combining parameters: \(\widetildex=r_A\,x\), \(\widetildeC=Cr_A/r_C\), \(\widetildeK_C=K_Cr_A/r_C\). Therefore, the equations become:

In the rescaled equations (2), the units of parameters and variables are: \([\widetildex]\) (mM day⁻¹) and \([\widetildeC]=[\widetildeK_C]\) (mM). Therefore, the solution of nitrate dynamics only depends on three parameters (γ, K_A and \(\widetildeK_C\)) and three initial conditions (A₀, \(\widetildeC(0)\) and \(\widetildex(0)\)). Since the affinities are very small (K_A ≈ 0.01 mM, \(\widetildeK_C\approx 0.01\,\rmmM\)), the solution of biomass activity approximately equals \(\widetildex=\widetildex(0)\rme^\gamma t\) before the time at which growth stops t* (Fig. 2). So the resource dynamics before t* are approximately \(A\,=\) \(A_-\widetildex(0)(\rme^\gamma t-1)/\gamma \) and \(\widetildeC=\widetildeC(0)-\widetildex(0)(\rme^\gamma t-1)/\gamma \). Accordingly, the time at which growth stops is given by \(t^* =\log (\min (A_,\widetildeC(0))\gamma /\widetildex(0)+1)/\gamma \). If \(\widetildeC(0) < A_\), the nitrate dynamics after t* and before running out are given by \(A=A(t^* )\,-\,(\gamma \widetildeC(0)\,+\) \(\widetildex(0))(t-t^* )\). As a result, the nitrate consumption rate after t* is \(\gamma \widetildeC(0)\) larger than the initial rate \(\widetildex(0)\). Therefore, the two key parameters of the model are \(\widetildex(0)\) and \(\gamma \widetildeC(0)\) which are both rates (in mM day⁻¹).

Least-squares fitting scheme

To infer the model parameters from the metabolite measurement, we use the least-squares fitting scheme to find the closest dynamic curves to the time-series data. Our metabolite measurement including the time points (\(\underlinet^-=[t_1^-,t_2^-,…,t_N^-]\)) and nitrate amount (\(\underlinea^-=[a_1^-,a_2^-,…,a_N^-]\)) for each CHL- sample, and the measurements of \(\underlinet^+\) and \(\underlinea^+\) for a corresponding chloramphenicol-treated sample. We set up the loss function as the mean-squared error:

Here, the functions A(t) and A^c(t) are theoretical solutions of the consumer-resource model (2) for non-chloramphenicol and chloramphenicol conditions, respectively. Because the nitrate dynamics A(t) and A^c(t) are determined by the parameter set \(\Theta =\\widetildex(0),\widetildeC(0),A_,A_^c,\gamma ,K_A,\widetildeK_C\\), we minimize the loss function L(Θ) to get the optimal model parameters Θ*. We note to the readers that three parameters are fixed (γ = 4.8 day⁻¹, \(K_A=\widetildeK_C=0.01\,\rmmM\)) as justified by the sensitivity analysis in the following paragraph. Note that these parameters were globally fixed across all the data for CAF soils. For other soils (IL, IN, CA), γ is fixed within each site but may vary for soils from different sites, the value of which is chosen in the regime where fit quality is insensitive to γ (see next section). The optimization algorithm is the interior-point method, which is built in the MATLAB fmincon function. The codes and data are available at the Open Science Framework (https://doi.org/10.17605/OSF.IO/CTF8K). The fitting errors over all samples are shown in Extended Data Fig. 3a,b, in which the root-mean-squared error (RMSE, \(\sqrtL(\Theta ^* )\)) and the error per data point (\(| A(t_k^-)-a_k^-| \) or \(| A^c(t_k^+)-a_k^+| \)) are normalized by the input value of nitrate (2 mM).

Sensitivity analysis on model parameters

Here we justify the decision to globally fix γ, K_A and \(\widetildeK_C\). We analysed the sensitivity of γ, K_A and \(\widetildeK_C\) on simulated dynamic data. To reflect the three typical dynamics (regimes) observed from the measurement, we simulated three nitrate curves by setting up the initial conditions to be \(\widetildex(0)=0.01,0.1\,\)\(\rmand\,0.001\,\rmmM\,\rmday^-1\) and \(\widetildeC(0)=0.005,0.05\,\rmand\,2\,\rmmM\), respectively. Other parameters are given by \(A_=A_^c=2\,\rmmM\), \(K_A=\widetildeK_C=0.01\,\rmmM\), γ = 4 day⁻¹. We then used different fixed parameter values to fit the three examples. In the first row of Extended Data Fig. 3c, we used different fixed γ values—from γ = 2 day⁻¹ to γ = 6 day⁻¹—to fit three simulations. We demonstrate very small mismatches (RMSE <5%) from these variations of parameter values, which are almost invisible in Regime I and Regime II fittings. In the second and the third row of Extended Data Fig. 3c, we use different fixed K_A and \(\widetildeK_C\) values—from 10⁻⁴ mM to 1 mM—to fit three simulations. When K_A < 0.1 mM or \(\widetildeK_C < 0.1\,\rmmM\), the mismatches were again very small (RMSE <1%) and invisible. These results indicate that the fixed values of γ, K_A and \(\widetildeK_C\) are insensitive in large ranges.

Determination of regime boundary with model parameters

To define the regime boundaries, we examined the distributions of each parameter’s value. \(\widetildex(0)\) had a bimodal distribution (Extended Data Fig. 3d). This bi-modality becomes more evident when we separately observe its distribution from the left half (perturbed pH < 4) and right half (perturbed pH > 6) of the parameter space displayed in the perturbed pH versus native pH grid in Fig. 3c (Extended Data Fig. 3e). Therefore, we set the threshold for the \(\widetildex(0)\) boundary where these two modes are separated (\(\widetildex(0)\) = 0.05). The distribution of \(\gamma \widetildeC(0)\) exhibited a significant mode around 0, prompting us to set the threshold (\(\gamma \widetildeC(0)\) = 1.5) at the tail region, where the \(\gamma \widetildeC(0)\) threshold also separated the Regime III samples in the top left quadrant of the \(\widetildex(0)\) versus \(\gamma \widetildeC(0)\) scatter plot (Fig. 3a). The separation of Regime I and Regime II data points may not be clear cut in the \(\widetildex(0)\) versus \(\gamma \widetildeC(0)\) scatter plot (Fig. 3a).

Sequence data analysis

Sequencing data preprocessing and assigning taxonomy to ASVs with DADA2

Raw Illumina sequencing reads were stripped of primers, truncated of Phred quality score below 2, trimmed to length 263 for forward reads and 189 for reverse reads (ensuring a 25-nucleotide overlap for most reads), and filtered to a maximum expected error of 4 based on Phred scores; this preprocessing was performed with USEARCH v.11.0⁶⁸. The filtered reads were then processed with DADA2 v.1.18 following the developers’ recommended pipeline⁶⁹. In brief, forward and reverse reads were denoised separately, then merged and filtered for chimeras. For greater sensitivity, ASV inference was performed using the DADA2 pseudo-pooling mode, pooling samples by soil. After processing, the sequencing depth of denoised samples was 10⁴–10⁶ reads per sample. Low-abundance ASVs were dropped (≤10 total reads across all 1,085 samples), retaining 34,696 ASVs for further analysis. Taxonomy was assigned by DADA2 using the SILVA database v.138.1, typically at the genus level, but with species-level attribution recorded in cases of a 100% sequence match. R scripts used for DADA2 sequencing data preprocessing were deposited at the Open Science Framework (https://doi.org/10.17605/OSF.IO/CTF8K).

Computing absolute abundance with internal standards of each ASV per sample

As an internal control, we verified that the ASVs corresponding to the two internal standard genera Escherichia–Shigella and Parabacteroides were highly correlated with each other as expected (Pearson correlation (ρ) = 0.94). These ASVs were removed from the table and combined into a single reference vector of ‘spike-in counts’. The spike-in counts constituted 8.9 ± 8.8% of the total reads in each sample. For downstream analysis, the raw ASV counts in a sample were divided by the spike-in counts of the internal standard per sample to obtain the absolute abundance of the ASV in a sample. Total biomass per sample was obtained by dividing the total raw read counts with the spike-in counts of the sample.

Differential abundance analysis to identify enriched ASVs

We conducted differential abundance analysis to statistically determine which ASVs were significantly enriched in the nutrient-limiting regime (Regime II) or the resurgent growth regime (Regime III), respectively. To do so, we identified enriched ASVs for each perturbed pH condition in each native soil comparing endpoint chloramphenicol-untreated samples with endpoint chloramphenicol-treated samples. For each native soil, we then compiled a list of enriched ASVs by aggregating a union set of enriched ASVs across perturbed conditions that belong to Regime II (or Regime III). To remove ASVs that could be false-positive nitrate reducers, we similarly performed differential abundance analysis to identify ASVs that are enriched in no-nitrate controls (nitrate⁻) by comparing endpoint chloramphenicol-untreated (−Chl, nitrate⁻) samples with endpoint chloramphenicol-treated (+Chl, nitrate⁻) samples. This filtering was done when inferring nitrate reducer biomass (Extended Data Fig. 4e,f) and inferring the Regime III strains (Extended Data Fig. 6c–e). For each native soil, we only had nitrate⁻ controls for the condition without acidic/basic perturbation. We assumed that these enriched ASVs in no-nitrate conditions (NNresponders) without acid/base perturbation would also be false-positive nitrate reducers in other acidic or basic perturbation levels. For each native soil, we filtered out these false-positive NNresponders from the aggregated list of Regime II (or Regime III) enriched ASVs.

To identify the ASVs enriched for each perturbed pH level, it was necessary to determine what change in recorded abundance constitutes a significant change, relative to what might be expected for purely stochastic reasons. The relevant null model would combine sampling and sequencing noise with the stochasticity of ecological dynamics over a four-day incubation, and cannot be derived from first principles. However, since all measurements were performed in triplicate with independent incubations, the relevant null model can be determined empirically. The deviations of replicate–replicate comparisons from 1:1 line were well-described by an effective model combining two independent contributions, a Gaussian noise of fractional magnitude c_frac and a constant Gaussian noise of magnitude c₀ reads, such that repeated measurements (over biological replicates) of an ASV with mean abundance n counts are approximately Gaussian-distributed with a standard deviation of \(\sigma (c_,c_\textfrac)=\sqrt(c_\textfracn)^2+c_^2\) counts. In this expression, c_frac was estimated from moderate-abundance ASVs (>50 counts) for which the other noise term is negligible; and c₀ was then determined as the value for which 67% of replicate–replicate comparisons are within ±σ(c₀, c_frac) of each other, as expected for 1-sigma deviations. This noise model was inferred separately for each soil and each perturbed pH level, as the corresponding samples were processed independently in different sequencing runs. For example, the parameters in Soil 11 were c_frac = 0.21 ± 0.04 and c₀ = 4.5 ± 0.7 counts (Extended Data Fig. 9i).

The model was used to compute the z-scores for the enrichments of absolute ASV abundances in non-chloramphenicol treatments against chloramphenicol-treated controls (three independent z-scores from three replicate pairs; rep1–rep1, rep2–rep2 and rep3–rep3). The median z-score was assigned to each ASV for each perturbed condition. In consideration of ASVs with 0 read count in samples with or without chloramnphenicol treatment, all raw ASV counts were augmented by a pseudocount of 0.5 and divided by the per-sample spike-in counts, yielding values that can be interpreted as the absolute biomass of each taxon (up to a factor corresponding to the copy number of the 16S operon), measured in units where 1 means as many 16S fragments as the number of DNA molecules in the spike-in. Significantly enriched ASVs were identified in each perturbed condition as those with z-scores greater than z = Φ⁻¹(1 − α/2n_ASV), where Φ⁻¹(x) is the inverse cumulative distribution function of the standard normal distribution, α = 0.05, and n_ASV is the number of non-zero ASVs in a given sample. This critical z-score (z = 4.2, when n_ASV = 2,000 for enriched ASVs and z = 4.3, when n_ASV = 2,500 for filtering no-nitrate responders (NNresponders)) corresponds to a two-tailed Bonferroni-corrected hypothesis test at significance level α under the null hypothesis that counts in the chloramphenicol-treated and untreated conditions are drawn from the same distribution. These analyses were performed using custom MATLAB (Mathworks) and R scripts, which are deposited at the Open Science Framework (https://doi.org/10.17605/OSF.IO/CTF8K); for additional technical details, the reader is referred to the detailed comments in these scripts.

NMF analysis on phylum-level growth folds

To analyse the abundance change at the phylum level, we compute the growth fold of each phylum at each condition. For each phylum, we compute the absolute abundance by aggregating the abundances of all ASVs within that phylum. Taking chloramphenicol-treated abundance (Abs⁺) as the reference abundance and non-chloramphenicol abundance (Abs⁻) as the endpoint abundance (where Abs denotes taxon abundance normalized to internal standard), the logarithm of the growth fold for phylum i and condition j is given by \(g_ij=\log (\rmAbs_ij^-+1^-3)-\log (\rmAbs_ij^++1^-3)\). Note that we use chloramphenicol-treated abundance as reference instead of the initial abundance (at T₀), to account for any effects on read counts unrelated to growth which would be common between chloramphenicol-treated and untreated conditions (for example, direct effect of acid/base addition), allowing us to focus only on growth-mediated abundance changes. We also set all negative g_ij to 0 since we are focusing on growth. For all 130 conditions (10 soils × 13 perturbations) and 40 phyla, the phylum-level growth folds G is a 40 × 130 matrix. For each phylum, the row vector \(\overrightarrowg_i\) represents how it grows under different conditions (see Extended Data Fig. 5b for the growth vectors of the first 10 phyla). In order to reduce the dimensionality of the growth matrix and extract the main features of the growth vectors, we use NMF to decompose the growth matrix G = W × H into 2 factors, which retain 93.36% of the original G matrix variation. Here, the feature matrix H is of size 2 × 130, and the 2 rows \(\overrightarrowh_1\) and \(\overrightarrowh_2\) are 2 modes of growth vectors (shown in Extended Data Fig. 5c). Therefore, the growth vector of phylum i is thus decomposed as \(\overrightarrowg_i\approx w_i1\overrightarrowh_1+w_i2\overrightarrowh_2\), while the weights w_i1 and w_i2 are from the 40 × 2 weight matrix W. The weights of all 40 phyla are plotted in Extended Data Fig. 5c, showing that Bacillota is mostly composed of the second mode \(\overrightarrowh_2\) and other phyla are mostly composed of the first mode \(\overrightarrowh_1\). Additionally, Bacteroidota and Pseudomonadota show the most significance in the first mode.

Genotyping enriched ASVs with PICRUSt2

To understand what traits make resurgent growth strains unique, we used PICRUSt2 v.2.5.2²⁸ to infer putative genotypes of the enriched ASVs in the resurgent growth regime (Regime III) (Extended Data Fig. 6g). Using the script place_seqs.py from PICRUSt2, we matched the representative 16S rRNA sequences of each ASV to PICRUSt2’s curated reference genome database (multiple sequence alignment). Then, using the hsp.py script from PICRUSt2 with default parameters, we predicted KEGG orthologues (KO) abundance of each ASV with the matched reference genome (hidden-state prediction). To narrow down to KOs or genes related to denitrification and DNRA, we focused on nitrate reductase in denitrification (narG/K00370, narH/K00371, narI/K00374, napA/K02567 and napB/K02567) and nitrite reductase to ammonium (nirB/K00362, nirD/K00363, nrfA/K03385 and nrfH/K15876). To track which KOs were enriched at which pH in the 89 families used in the peak pH analysis (see Supplementary Information, ‘Determination of peak pH for each family’), we summed the relative abundance (reads/total reads of each perturbed pH level in non-chloramphenicol condition) of the ASVs belonging to each family that possessed at least 1 predicted gene respectively for narGHI, napAB, nirBD and nrfAH. Then, we plotted their relative abundance values across pH for all soils, indicated by the intensity of the point’s colours (Extended Data Fig. 6g).

Taxonomy of growing strains in Regime III varies with soil native pH

To further investigate whether the taxonomic identity of resurgent growth (Regime III) strains varies across natural pH environments, we performed a regularized regression analysis to see if we can predict the native pH level of the source soil from the presence or absence of taxa that grow in Regime III at the ASV, species, genus, family, or higher taxonomic levels. The resurgent growth strains were determined by the differential abundance analysis as described previously. We used the sequencing data to build a matrix where the rows are samples (including three biological replicates) belonging to the resurgent growth regime (Regime III), where each row has a corresponding native pH value of the original soil. There are ten source soils with different native pH levels, and each soil has 3–6 pH-perturbed samples (replicates) of which metabolite dynamics are classified as Regime III. The matrix’s columns are different taxa belonging to the identified Resurgent growth strains, either in ASV, species, genus, family or higher levels. Each element of the matrix is 0 if absent and 1 if present in the sequencing data of the sample. Because the presence and absence of taxa can randomly depend on the random sampling depth of each sample, we test varying threshold values (0, 0.001 or 0.005 relative abundance) to call the taxa present if their relative abundance is greater than the threshold (effects shown in Extended Data Fig. 8k).

The regularized regression was performed to predict the native pH of the source soil of the samples from the presence and absence of taxa using only additive terms and LASSO regularization to avoid overfitting⁷⁰. To estimate the regularization hyperparameter, tenfold cross-validation was performed on the samples from ten different soils with different native pH levels. All models were fit using the package glmnet in R v.4.1.4. To make predictions of the native pH, we used two strategies. First, ‘in-sample’ predictions used all available data points to fit the regression coefficients and predicted native pH using those coefficients. Second, to ask whether we can still predict the native pH without the model seeing the samples belonging to that specific native pH level, we implemented a leave-one-soil-out (LOSO) procedure, where all the perturbed samples from one native soil were left out as a test set, and the model was trained on the remaining data to fit the regression coefficients. Then, we used the model to predict the native pH of the left-out samples (out-of-sample prediction). The observed versus predicted pH values are shown in the scatter plots (Extended Data Fig. 8h). The prediction quality (R²) was computed using the mean predicted and mean observed native pH levels for each soil (for different taxonomic levels and prediction strategies, see Extended Data Fig. 8j,k; negative R² values indicate the predictions are worse than just predicting the pH as the mean predicted pH). To ascertain that our high prediction quality was not a random artefact, we randomly permuted the native pH values of our soils 1,000 times and then predicted in-sample the native pH to obtain 1,000 R² values under permutation and used this distribution to compute a P value (0.012) for the observed R² obtained with our true native pH values (black arrow, Extended Data Fig. 8l).

Testing the effect of different bases and salts on nutrient release

To see the effects of different bases (NaOH and KOH) on nitrate reduction dynamics, we added different concentrations of NaOH and KOH (final concentration of 0, 8, 16 and 24 mM in the slurry), following the same protocol previously described (without chloramphenicol), to measure the nitrate and nitrite dynamics (Extended Data Fig. 2g, using Soil 6; Supplementary Table 1). In addition, to test the effects of Na⁺, K⁺ and Cl⁻ separately, we added different concentrations of salts (NaCl and KCl) (without chloramphenicol and without adding any acid or base) and measured the metabolite dynamics (Extended Data Fig. 2g).

Nutrient amendment experiments with slurries

To experimentally determine what nutrient was limiting growth in the nutrient-limiting regime, we conducted nutrient amendment experiments respectively with glucose, succinate, sodium acetate, ammonium chloride (NH₄Cl), monosodium phosphate (NaH₂PO₄) and sodium sulfate (Na₂SO₄) (for results, see Fig. 5d and Extended Data Fig. 2h). Among them, succinate (pK_a = 4.21 and 5.64, 25 °C), acetate (pK_a = 4.76, 25 °C), and phosphate (pK_a = 2.2, 7.2 and 12.4, 25 °C) were strong candidates for the limiting nutrient according to our soil nutrient release hypothesis, due to their anionic nature in mid-range pH (5–7). The incubation was conducted following the same protocol using Soil 6 (Supplementary Table 1) without chloramphenicol and without adding any acid/base. Concentrations were either in mM C, mM N, mM S or mM P with final concentrations in slurry varying from 0 to 5 mM, each in triplicate. Because we have previously tested the effect of Na⁺ and Cl⁻ to be negligible in nitrate dynamics, the effect of these amendments can be attributed solely to C, N, S or P nutrients other than Na⁺ and Cl⁻.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.