Functional connectomics reveals general wiring rule in mouse visual cortex

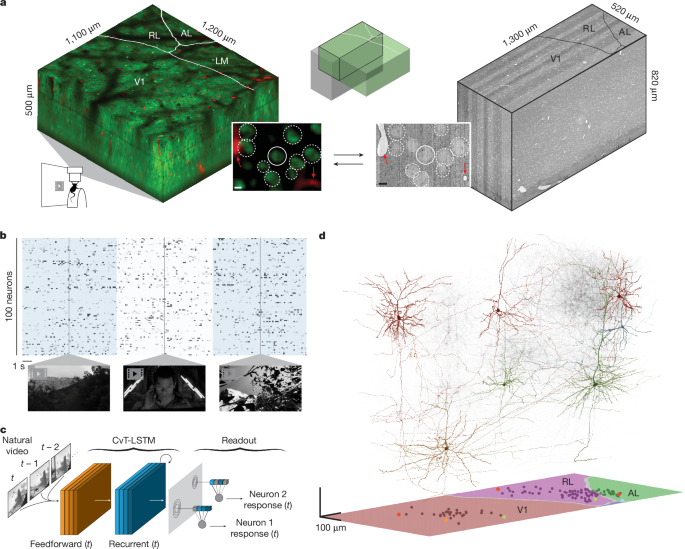
The MICrONS dataset

The MICrONS dataset was collected in a single mouse as described in ref. ¹⁴, including neurophysiological data collection, visual stimulation, stimulus composition, EM data collection, automatic EM segmentation and reconstruction, EM synapse detection, manual EM proofreading, volume coregistration and manual soma–soma matching between the functional and EM volumes. The sections ‘Neurophysiological experiments’, ‘Visual stimulation’ and ‘Validation of the digital twin model’ below are specific to additional experiments described in Extended Data Figs. 2, 4 and 8.

Neurophysiological experiments

All procedures were approved by the Institutional Animal Care and Use Committee of Baylor College of Medicine. Animals were housed in a room with 20–22 °C, 30−70% humidity, 12 h light:12 h dark cycle room, with experiments performed during the subjective night. Ten mice (Mus musculus, 3 female, 7 males, 78–190 days old at first experimental scan) expressing GCaMP6s in excitatory neurons via Slc17a7-Cre and Ai162 transgenic lines (provided by H. Zeng; JAX stock 023527 and 031562, respectively) were anaesthetized and a 4-mm craniotomy was made over the visual cortex of the right hemisphere as described previously^47,48.

Mice were head-mounted above a cylindrical treadmill and calcium imaging was performed with a mesoscope¹⁵ as described¹⁴, with surface power not exceeding 20 mW, depth constant of 220 μm, and greatest laser power of ~86 mW used at approximately 400 μm from the surface.

The cranial window was levelled with regard to the objective with six degrees of freedom. Pixel-wise responses from a region of interest spanning the cortical window (3,600 × 4,000 μm, 0.2 pixels per μm, 200 μm from surface, 2.5 Hz) to drifting bar stimuli were used to generate a sign map for delineating visual areas³⁰.

For the validation data in Extended Data Figs. 2, 4 and 8, our target imaging site was a 1,200 × 1,100 μm² area spanning L2–L5 at the conjunction of lateral V1 and three lateral higher visual areas: AL, LM and RL. This resulted in an imaging volume that was roughly 50% V1 and 50% HVA. This target was chosen in order to mimic the area membership and functional property distribution in the MICrONS animal. Each scan was performed at 6.3 Hz, collecting eight 620 × 1,100 μm² fields per frame at 0.4 pixels per μm xy resolution to tile a 1,190–1,200 × 1,100 μm² field of view at 4 depths (2 planes per depth, 40−50 μm overlap between coplanar fields). The 4 imaging planes were distributed across layers with at least 50 μm spacing, with two planes in L2/3 (depths: 180 μm, 230 μm), one in L4 (325 μm), and one in L5 (400 μm).

Video of the animal’s eye and face was captured throughout the experiment. A hot mirror (Thorlabs FM02) positioned between the animal’s left eye and the stimulus monitor was used to reflect an IR image onto a camera (Genie Nano C1920M, Teledyne Dalsa) without obscuring the visual stimulus. The position of the mirror and camera were manually calibrated per session and focused on the pupil. Field of view was manually cropped for each session. The field of view contained the left eye in its entirety, 212–330 pixels height × 262–424 pixels width at 20 Hz. Frame times were time-stamped in the behavioural clock for alignment to the stimulus and scan frame times. Video was compressed using Labview’s MJPEG codec with quality constant of 600 and stored the frames in AVI file.

Light diffusing from the laser during scanning through the pupil was used to capture pupil diameter and eye movements. A DeepLabCut model⁴⁹ was trained on 17 manually labelled samples from 11 animals to label each frame of the compressed eye video (intraframe only H.264 compression, CRF:17) with 8 eyelid points and 8 pupil points at cardinal and intercardinal positions. Pupil points with likelihood >0.9 (all 8 in 69.8−99.2% of frames per scan) were fit with the smallest enclosing circle, and the radius and centre of this circle was extracted. Frames with <3 pupil points with likelihood >0.9 (<1.1% frames per scan), or producing a circle fit with outlier >5.5 × s.d. from the mean in any of the three parameters (centre x, centre y, radius, <0.1% frames per scan) were discarded (total <1.2% frames per scan). Gaps were filled with linear interpolation.

The mouse was head-restrained during imaging but could walk on a treadmill. Rostro-caudal treadmill movement was measured using a rotary optical encoder (Accu-Coder 15T-01SF-2000NV1ROC-F03-S1) with a resolution of 8,000 pulses per revolution, and was recorded at ~100 Hz in order to extract locomotion velocity.

Visual stimulation

For the validation data in Extended Data Figs. 2, 4 and 8, monitor size and positioning relative to the mouse were as described¹⁴, with the exception of replacing the dot stimulus for monitor positioning with 10 × 10 grid tiling a central square (approximately 90° width and height) with 10 repetitions of 200 ms presentation at each location.

A photodiode (TAOS TSL253) was sealed to the top left corner of the monitor, and the voltage was recorded at 10 kHz and time-stamped with a 10 MHz behaviour clock. Simultaneous measurement with a luminance meter (LS-100 Konica Minolta) perpendicular to and targeting the centre of the monitor was used to generate a lookup table for linear interpolation between photodiode voltage and monitor luminance in cd m⁻² for 16 equidistant values from 0–255, and 1 baseline value with the monitor unpowered.

At the beginning of each experimental session, we collected photodiode voltage for 52 full-screen pixel values from 0 to 255 for 1-s trials. The mean photodiode voltage for each trial was collected with an 800-ms boxcar window with 200-ms offset. The voltage was converted to luminance using previously measured relationship between photodiode voltage and luminance and the resulting luminance versus voltage curve was fit with the function L = B + A × P^γ, where L is the measured luminance for pixel value P, and the γ of the monitor was fit as 1.73. All stimuli were shown without linearizing the monitor (that is, with monitor in normal gamma mode).

During the stimulus presentation, display frame sequence information was encoded in a three-level signal, derived from the photodiode, according to the binary encoding of the display frame (flip) number assigned in order. This signal underwent a sine convolution, allowing for local peak detection to recover the binary signal together with its behavioural time stamps. The encoded binary signal was reconstructed for >93% of the flips. Each flip was time-stamped by a stimulus clock (MasterClock PCIe-OSC-HSO-2 card). A linear fit was applied to the flip time stamps in the behavioural and stimulus clocks, and the parameters of that fit were used to align stimulus display frames with scanner and camera frames. The mean photodiode voltage of the sequence encoding signal at pixel values 0 and 255 was used to estimate the luminance range of the monitor during the stimulus, with minimum values of approximately 0.003–0.60 cd m⁻² and maximum values of approximately 8.68–10.28 cd m⁻².

Preprocessing of neural responses and behavioural data

Fluorescence traces from the MICrONS dataset and the additional data for Extended Data Figs. 2, 4 and 8 were detrended, deconvolved and aligned to stimulus and behaviour as described²⁶, and all traces were resampled at 29.967 Hz. Possible redundant traces, where a single neuron produced segmented masks in multiple imaging fields, were all kept for downstream model training. We elected to remove one of the 14 released scans from the analysis (session 7, scan_idx 4) due to compromised optics (water ran out from under the objective for ~20 min), leaving 13 scans.

Model architecture and training of the digital twin model

The model architecture and training for the digital twin model used for assessing in silico signal correlation, feature weight similarity, and RF centre distance is the same as the CvT-LSTM model described in ref. ²⁶.

In brief, the core network of the CvT-LSTM models was trained on eight scans collected from eight mice with natural video stimuli to capture cortical representations of visual stimuli shared across mice. The parameters of the core network are then frozen, and the rest of the network parameters are trained for each scan with trials where natural videos are shown in the MICrONS dataset. Trials were excluded from model training if more than 25% of their pupil frames were untrackable. This issue most commonly arose when the animal closed its eye, rendering the functional relationship between neural activity and the visible stimulus ambiguous. The number of excluded trials varied across scans, ranging from 2 to 123 per scan, representing 0.6–38.0% of total trials.

To assess orientation tuning similarity (Extended Data Figs. 8, 9, 10 and 13), the parameters of the core of the CvT-LSTM model above were frozen, and the rest of the network parameters are fine-tuned with both natural videos and oriented noise stimuli available from the MICrONS dataset to improve alignment between in vivo and in silico orientation tuning.

Functional unit inclusion criteria

In order to focus our analyses on neurons that are visually responsive and well modelled by the digital twin, we applied a dual functional threshold over two metrics (in vivo reliability and model prediction performance) prior to all analyses related to signal correlation, RF centre distance and feature weight similarity.

In vivo reliability threshold

In order to estimate the reliability of neuronal responses to visual stimuli, we computed the upper bound of correlation coefficients for each neuron (CC_max; Schoppe et al.⁵⁰) across 60 s of natural video stimuli repeated 10 times across the stimulus period (10 min total). CC_max was computed as:

where y is the in vivo responses, and N is the number of trials. A threshold of CC_max >0.4 was applied. Where more than one 2P functional unit was matched to a given EM unit, the functional trace with the higher oracle score was used for analysis.

Model prediction performance threshold

In order to focus our analyses on neurons for which adequate model performance indicated sufficiently accurate representation of the neuronal tuning features, we computed the test correlation coefficient on the withheld oracle test dataset, which was not part of the training set. Test correlation coefficients (CC_abs) were computed as:

where x is the in silico response and y is the in vivo response. A threshold of CC_abs >0.2 was applied.

144 out of 148 presynaptic neurons and 3,920 out of 4,811 postsynaptic neurons passed the dual functional unit inclusion criteria.

Oracle score

The oracle score was computed for all units as described in the accompanying Article¹⁴. Oracle score is later used to select presynaptic neurons for morphological proofreading.

2P–EM matching

The matching between 2P functional units and EM cells aligns closely with table coregistration_manual_v4¹⁴ with some additional restrictions applied. First, the matches to the excluded scan described in ‘Preprocessing of neural responses and behavioural data’ were removed. Then, two thresholds were applied directly to the table (residual <20 and score >−10).

Morphological proofreading

Whereas automation of the EM segmentation has progressed to where dense reconstruction is possible at the millimetre scale, even state-of-the-art methods still leave imperfections in the graph relative to human expert performance. The two categories of reconstruction error are false merges (the incorrect grouping of segmented objects, such as including an axon or dendrite that does not belong to a specific soma) and false splits (the incorrect separation of objects, such as excluding an axon or dendrite that does belong to a specific soma). These errors lead to incorrect associations between pre- and postsynaptic partners and ultimately an incorrect connectivity graph. Proofreading corrects false merges by ‘cleaning’ the reconstruction (removing incorrectly associated segments), and corrects false splits by ‘extending’ the reconstruction (adding back missing segments). We used two proofreading approaches in this study: manual and automatic. ‘Manual proofreaders’ were trained to both clean and extend reconstructions to a high degree of accuracy, as validated by expert neuroanatomists. All of the presynaptic cells in this study were manually proofread. The manual proofreading protocol can be found in the primary dataset Article¹⁴. For the rest of the cells (postsynaptic and control neurons), we used the NEURD package²⁸ to perform automated proofreading. Automated proofreading cleans reconstructions to a high degree of accuracy relative to manual proofreaders, but it does not extend reconstructions.

Dendritic proofreading

At baseline, reconstructed dendrites were generally complete and required little extension⁵¹. However, they often contained false merges that required cleaning⁵¹. The dendrites of all of the presynaptic neurons were manually cleaned and extended. The dendrites of other neurons were cleaned with NEURD²⁸.

Axonal proofreading

At baseline, reconstructed axons require both cleaning and extension⁵¹. Only the axons of presynaptic neurons were manually cleaned and extended. In order to balance morphological completeness (per neuron) and coverage (across projection types), we extended axons to varying degrees of completion. Specifically, we performed full manual proofreading on a subset of neurons (n = 84), which involved thoroughly cleaning and extending all axonal branches throughout the dataset. For the remaining neurons (n = 64), we applied partial proofreading, focusing exclusively on extending axonal branches that were pre-screened to feedback from HVA to V1. The full list of proofread presynaptic neurons, their area and layer membership, and whether they were fully or partially proofread is included in Supplementary Table 1, and a subset of proofread axons are shown in Extended Data Fig. 1.

Manual proofreading completion

As part of manual proofreading protocol¹⁴, proofreaders were instructed to leave annotations at the termination of every neurite indicating its status, whether natural or incomplete. From these annotations, we estimate the frequency of untraceable ends, a rough indicator of incompleteness. For dendrites, the median neuron had a percentage of untraceable ends of 1% (n = 148 fully proofread dendritic arbors). For axons, the median neuron had a percentage of untraceable ends (not including those at dataset boundaries) of 43% (n = 84 fully proofread axonal arbors).

Presynaptic neuron selection

Our approach for selecting presynaptic neurons for manual proofreading was designed to enrich for higher-order connectivity motifs within and (especially) across visual areas. Because connection probability drops off with distance⁵², we elected to initially focus proofreading efforts on spatially clustered cells in two cylindrical columns spanning cortical layers 2–5, with the first column located in V1 and the second located in RL. Column centres were chosen according to retinotopic maps, as it has been shown that inter-areal projections are retinotopically matched^29,43. During the proofreading process we added an additional column in V1 and another spanning the RL and AL border, to increase coverage of the volume. Finally, a few HVA cells that were postsynaptic to proofread V1 cells were chosen to enrich for higher-order motifs (n = 9).

All neurons selected for proofreading had an oracle score greater than 0.25 and model test correlation (model predictive performance from an intermediate version of the digital twin) greater than 0.15. The first 40 neurons were selected by experienced neuroscientists unblinded to functional properties for an emphasis on functional diversity. All remaining neurons were chosen blind to functional properties.

Anatomical controls

In order to control for anatomy at the axonal scale, we recruited all visually responsive, well predicted, functionally matched excitatory neurons (CC_max >0.4, CC_abs >0.2) that are located in the same region as the postsynaptic target, but are not observed to form a synapse with the presynaptic neuron (same-region control). Area membership labels per neuron were used from the MICrONS release¹⁴. Additionally, control candidates that meet criteria for both the same-region control and the ADP control (described below) will only be included in ADP control.

In order to control for anatomy at the synaptic scale, we recruited all visually responsive, well predicted, functionally matched excitatory neurons (CC_max >0.4, CC_abs >0.2) with a dendritic skeleton passing within 5 μm of the presynaptic neuron axonal synapse in the presynaptic axonal arbor (3D euclidean distance), but which are not observed to form a synapse with the presynaptic neuron (ADP control). Presynaptic axonal skeletons were computed using the pcg_skel package developed by collaborators at the Allen Institute for Brain Science^53,54. For postsynaptic dendritic skeletons, we used the automatically proofread and skeletonized dendritic arbors as described²⁸.

To compute the axon–dendrite co-travel distance (L_d) between a pair of neurons, we first discretized both the axonal skeleton of one neuron and the dendritic skeleton of the other neuron so that no edge exceeded a length of 1 μm. Next, we identified all pairs of vertices from the two skeletons that were within 5 μm of each other by performing spatial queries using the KDTree query_ball_tree method from the scipy.spatial module in SciPy⁵⁵. From these proximal vertices (proximity), we identified the associated dendritic edges. The lengths of these dendritic edges were summed to obtain L_d.

Synapses were obtained from Table synapses_pni_2¹⁴ and were assigned to an ADP if they were within 3 μm of any vertex in the proximity.

In the case of the joint area and layer analysis (Fig. 4), candidates in both the same-region and ADP controls must additionally match the same layer classification as the postsynaptic target in order to be included. Layer assignment was performed as described⁵⁶.

Measuring functional similarities

In silico response correlations

To characterize the pairwise tuning similarity between two modelled neurons, we computed the Pearson correlation of their responses to 2,500 s of natural videos. The natural videos were fed in to the model as trials of 10 s. Model responses were generated at 29.967 Hz and Pearson correlations were computed after binning the responses into 500 ms non-overlapping bins and concatenating across trials.

In silico feature weight similarity and RF centre distance

The digital twin model architecture includes a shared core which is trained to represent spatiotemporal features in the stimulus input, and a final layer where the spatiotemporal features at a specific readout location are linearly weighted in order to produce the predicted activity of a specific neuron at the current time point²⁶. The readout location and linear feature weight are independently learned for each neuron. In order to measure the feature weight similarity between two units, we extract the linear feature weights from this final step as vector of length 512, and take the cosine similarity between the two vectors. In order to measure the RF centre distance between two units, we extract the readout location as 2D coordinates on the monitor, and take the angle between them with respect to the mouse’s eye, assuming the monitor is centred on, 15 cm away from, and normal to the surface of the mouse’s eye at the closest point.

In silico difference in preferred orientation

Two hundred and forty blocks of parametric directional visual stimuli (Monet) are shown to the model, with each 15-s block consisting of 16 trials of equally distributed and randomly ordered unique directions of motion between 0 and 360°. A modelled neuron’s direction tuning curve is computed as its mean responses to 16 directions averaged across blocks. We calculated the gOSI and the orientation selectivity index (OSI) from the modelled neuron’s tuning curve as follows:

where θ is the direction of the stimulus, R_θ is the mean modelled response to the stimulus at direction θ, and R_po and R_ortho are the mean modelled responses at the preferred and orthogonal orientation, respectively. The gOSI metric is based on the 1 − CircVar metric in ref. ⁵⁷, which is a vector-based method designed to reduce the uncertainty in quantifying orientation selectivity of responses, especially in cases where high throughput, unbiased recording methods return many cells with low orientation selectivity, as is the case with calcium imaging. Only neurons with gOSI >0.25 were included in the analyses in this Article. For neurons selected with our gOSI threshold >0.25, the computed OSI ranges from 0.43 to 0.99, with mean of 0.56. For both thresholds, the fraction of cells considered orientation tuned (57.4% of co-registered V1 neurons has gOSI >0.25, 62.7% of co-registered V1 neurons has OSI >0.4) is similar to those reported in other studies (72% in V1 layer 2/3 (ref. ¹), 62.9% in V1 layer 2/3 and 58.0% in V1 layer 4 (ref. ⁵⁸)). Unit-wise direction tuning curves are then parameterized by a mixture of two von Mises functions with an offset as described in²⁶. In brief, the model has the following form:

where α and β are the amplitudes of the two von Mises function, μ is the preferred direction, κ is the dispersion, and γ is the offset. The parameters are estimated through least squares optimization, minimizing \(\sum _\theta \mu ,\kappa \alpha ,\beta ,\gamma )-R_\theta )^2\). The preferred orientation of a neuron is taken as the modulus of μ to 180°.

Validation of the digital twin model

Validation of in silico signal correlations

To validate the in silico signal correlations generated by our digital twin model, we first established a benchmark for in vivo signal correlations. We began by determining the optimal number of stimulus repetitions for measuring in vivo signal correlations. Two mice were presented with 6 unique 10-s natural video clips, each repeated 60 times over a 60-min period. Based on the results shown in Extended Data Fig. 2a, we determined that ten repetitions per clip provided a reliable estimate of in vivo signal correlation while maintaining a reasonable experimental time for presenting a large number of clips in subsequent experiments.

With this optimal repetition count established, we conducted experiments with three mice using an expanded set of visual stimuli. These stimuli contained those presented in the MICrONS dataset as described¹⁴, including natural videos, global directional parametric stimuli (Monet), and local directional parametric stimuli (Trippy). Additionally, we presented 36 unique 10-s natural video clips, each repeated 10 times, totaling 60 min of stimulation. To facilitate comparison with the MICrONS dataset and establish a robust ground truth, we divided these 36 clips into two sets: a benchmark set of 30 clips repeated 10 times, serving as our ‘ground truth’ for signal correlation, and a MICrONS-equivalent set of 6 clips repeated 10 times, mimicking the amount of repeated natural clip data available in the MICrONS dataset.

For each mouse, we trained a digital twin model using the same architecture and training data as the MICrONS digital twin. This allowed us to generate three signal correlation matrices for comparison: an in vivo matrix computed from the MICrONS-equivalent set, an in silico matrix generated by the digital twin model using 250 novel natural video clips, and a benchmark matrix computed from the 30-clip set. To compare these matrices, we randomly sampled submatrices of signal correlations between 1,000 neurons. We then performed hierarchical clustering using Ward’s method on the benchmark matrix and used the resulting dendrogram to sort neurons. This sorting was applied to the MICrONS-equivalent and in silico matrices for visual comparison, as shown in Extended Data Fig. 2b. Following this initial comparison, we calculated the Pearson correlation coefficient between the corresponding entries in the lower triangles of the three matrices. To assess statistical significance, we employed a resampling approach, performing 1,000 random splits of the benchmark and MICrONS-equivalent sets, from which we estimated the standard deviation and resampling-based P value of the Pearson correlations. This comprehensive approach enabled us to evaluate how well our digital twin model’s in silico signal correlations matched the ground truth compared to in vivo measurements with limited data, thus validating the model’s performance in replicating neural response correlations.

Validation of RF centre

To validate the RF estimates of our digital twin model, we conducted additional experiments and analyses comparing in vivo and in silico RF measurements. We collected three additional functional scans using an expanded set of visual stimuli. These stimuli contained those presented in the MICrONS dataset¹⁴, including natural videos, global directional parametric stimuli (Monet), and local directional parametric stimuli (Trippy). Additionally, we presented 57.6 min of sparse noise stimuli. The sparse noise stimuli consisted of bright (pixel value 255) and dark (pixel value 0) square dots, each approximately 6° in visual angle, presented on a grey background (pixel value 127) in a randomized order. These dots were presented at 12 positions covering 70° of visual angle along both the horizontal and vertical axes of the screen. Each presentation lasted 200 ms, and each condition was repeated 60 times.

We computed the in vivo STA RFs by cross-correlating the visual stimuli with deconvolved calcium traces. STAs for bright dots (on-STAs) and dark dots (off-STAs) were estimated independently and then combined by taking the pixel-wise maximum of the on- and off-STAs. We then presented the same sparse noise stimuli to the digital twin model and computed in silico STA RFs using the model responses. To assess STA quality, we generated response predictions by multiplying each neuron’s STA with the stimulus frames and compared these predictions to either the in vivo trial-averaged responses or model responses using Pearson correlation coefficients. Neurons with correlations greater than 0.2 were considered well-characterized. We then extracted the STA RF centres by fitting a 2D Gaussian to the STAs, with fits yielding an r-squared value over 0.5 considered well fit. Our analysis revealed that 44% of all imaged neurons had well-characterized, well-fit in vivo STAs.

To visualize the retinotopic maps measured with either in vivo STA or in silico STA, we converted the STA RF centres to azimuth and elevation angles, assuming the mouse was looking at the centre of the monitor. To exclude partially measured STAs, we included only neurons with well-characterized and well-fitted STA centres located in the central 8 × 8 square of the entire 12 × 12 stimulus grid (27% of all imaged neurons) for the analysis presented in Extended Data Fig. 4a–d,f,h. For the analysis in Extended Data Fig. 4e,g,i, we included neurons with the bottom 25% of response correlations that have STA centres located in the central 8 × 8 square.

Finally, we quantified the coherence of the retinotopic maps as Spearman’s correlation between cortical distances and retinotopic distance of 10,000 randomly sampled neuron pairs in a cortical region that does not contain a retinotopic reversal (shown as the dotted circled region in the retinotopic maps visualized in Extended Data Fig. 4).

Validation of orientation tuning

To validate in silico orientation tuning with in vivo orientation tuning, we collected three additional functional scans with an expanded set of stimuli. These stimuli contained those presented in the MICrONS dataset¹⁴, including natural videos, global directional parametric stimuli (Monet), and local directional parametric stimuli (Trippy). In addition, each stimulus contained an additional 40 min of trials, randomly intermixed, as follows:

• Unique global directional parametric stimulus (Monet): 120 seeds, 15 s each, 1 repeat per scan, 30 min total. Seeds conserved across all scans.

• Oracle global directional parametric stimulus (Monet): 4 seeds, 15 s each, 10 repeats, 10 min total. Seeds conserved across all scans.

We characterized both the in vivo orientation tuning in response to 30 min of global directional parametric stimulus (Monet; Extended Data Fig. 8a), as well as the in silico orientation tuning as described above for digital twin models with shared cores and readouts trained on neurons from the same scans, in response to stimuli matching the composition and duration of the MICrONS release scans (Extended Data Fig. 8b). When we applied a threshold of gOSI >0.25, we found that 95% of cells had an absolute difference between their in silico and in vivo preferred orientations less than 19.7°.

Statistics and reproducibility

All functional and anatomical data used for functional connectomics analysis in this Article were collected from a single mouse. No sample size calculation was performed a priori for this mouse, and sample sizes (number of connections tested) were determined by using all available data for each experimental group, matching or exceeding previous studies of similar design. Within the context of this single mouse, we treated pairs of neurons as independent samples for statistical analysis. For the validation of in silico properties in Extended Data Figs. 2, 4 and 8, we reproduced the validation results in three mice, with this number of validation mice chosen empirically without formal sample size calculations.

Statistical analysis of mean signal correlations

We employed paired t-tests to compare signal correlations between presynaptic neurons and three groups of potential target neurons: connected postsynaptic neurons, ADP neurons, and same-region control neurons. Our analysis focused on presynaptic neurons with more than ten postsynaptic targets for each projection type to ensure robust comparisons. For each presynaptic neuron, we computed mean signal correlations with its synaptically connected postsynaptic targets, ADP neurons (neurons with dendrites in proximity to the presynaptic axon but not synaptically connected), and same-region control neurons (neurons in the same brain region but without proximal axon–dendrite contacts). We then performed paired t-tests to compare these mean correlations. For example, to compare connected and ADP neuron pairs, we conducted a paired t-test between each presynaptic neuron’s mean signal correlation with its postsynaptic targets versus its mean signal correlation with ADP neurons. This approach allowed us to control for variability across presynaptic neurons while directly comparing their correlations with different target groups. All statistical analyses were performed using the scipy package in Python. We set the significance level (α) at 0.05 for all tests. To account for multiple comparisons, we adjusted P values using the Benjamini–Hochberg procedure as implemented in the statsmodels package.

Visualization of the relationship between L
_d, N
_syn/L
_d and the functional similarities

Visualization of L
_d

To quantify the changes in L_d as a function of functional similarities, we restrict our analysis to neuron pairs with no synaptic connections observed between them. We then follow these steps:

1. (1)

   We compute the mean L_d and mean functional similarities for each presynaptic neuron across all other neurons that no synaptic connections with the presynaptic neuron were observed.

2. (2)

   We subtract the presynaptic mean from each of the pairwise L_d and functional similarities between every neuron pair to compute ΔL_d and Δsimilarity .

3. (3)

   The neurons pairs are then binned by Δsimilarity and the average ΔL_d is computed for each bin.

4. (4)

   The standard deviation of average ΔL_d is estimated by bootstrapping. Specifically, we resampled the neuron pairs 1,000 times with replacement and repeated steps 1–3.

Only bins with more than ten connected neuron pairs and more than ten presynaptic neurons are included in the visualization.

Visualization of N
_syn/L
_d

To quantify the changes in synapse density, N_syn/L_d, as a function of functional similarities, we restrict our analysis to neuron pairs with positive L_d observed between them. We then follow these steps:

1. (1)

   We compute the mean N_syn/L_d and mean functional similarities for each presynaptic neuron across all other neurons that no synaptic connections with the presynaptic neuron were observed.

2. (2)

   We subtract the presynaptic mean from each of the pairwise N_syn/L_d and functional similarities between every neuron pair to compute ΔN_syn/L_d and Δsimilarity.

3. (3)

   The neurons pairs are then binned by Δsimilarity and the average ΔN_syn/L_d is computed for each bin.

4. (4)

   The standard deviation of average ΔL_d is estimated through bootstrapping. Specifically, we resampled the neuron pairs 1,000 times with replacement and repeated steps 1–3.

Only bins with more than ten connected neuron pairs and more than ten presynaptic neurons are included in the visualization.

Statistical modelling of like-to-like rules for different anatomical measurements

Axon–dendrite co-travel distance

L_d measures the distance dendrites of one neuron travel within 5 μm from another neuron’s axon. Most pairs of neurons’ axons and dendrites never come into close proximity with each other, and their L_d is zero. Thus, the L_d distribution is a non-negative continuous distribution with a substantial non-zero probability measure at zero L_d. Thus, we modelled L_d as a random variable following the Tweedie exponential dispersion family (with Tweedie index parameter ξ ∈ (1, 2)). Tweedie distributions with such index parameters are Poisson mixtures of gamma distributions, commonly used to model continuous data with exact zeros. We assume two neurons’ axons and dendrites travel within 5 μm at N proximity points, where N ~ Pois(λ^*), λ^* is the mean number of axonal dendritic proximal contacts of the Poisson distribution. When N > 0, we assume the distance dendrites travel within 5 μm at each proximal point z_i(i = 1, …, N) follows a Gamma distribution Gam(μ, ϕ). Under these assumptions, the total potential synapsing distance

where L_d = 0 when N = 0, follows a Tweedie distribution with 1 < ξ < 2. We then model the relationship between L_d, functional similarities Sim (for example, signal correlation, feature weight similarity and RF location distance between two neurons), and projection types Proj using a Tweedie-distributed GLMM with a log link function. For analysis at the brain area level, Proj is a nominal variable with four categories: V1 intra-area, HVA intra-area projections, feedforward projections and feedback projections. Similarly for analysis at the brain area and layer level, Proj is a nominal variable that contains categories of all area and layer projection types. We apply GLMMs for modelling as they have been recommended for accounting for multi-level data dependencies in datasets⁵⁹, such as the projection types and presynaptic neuron proofreading progress in our study. We specify the model as follows:

where:

• \(L_\rmd_ij\) is the axon–dendrite co-travel distance between presynaptic neuron i and postsynaptic neuron j.

• Sim_ij is the functional similarity between the neuron pair.

• Proj_k(i, j) is the projection type of the neuron pair (i, j).

• β₁, β₂ and β₃ are the fixed effect coefficients of the functional similarity, projection type and their interaction term, respectively.

• β₀ is the intercept.

• u_k(i, j),i is the random effect accounting for the projection type k and the proofread status associated with presynaptic neuron i.

• ϵ_ij is the error term, following a Tweedie distribution.

The coefficients β₁, β₂ and β₃ represent how functional similarities and projection types affect connectivity at the axonal scale. We fit the models for each functional similarity independently using the glmmTMB R package. The goodness-of-fit of the estimated models is reported as Nakagawa’s R squared, computed with the performance R package. We define the axonal-scale like-to-like coefficients for each functional similarity and projection type as the estimated linear association between each category of functional similarity conditioned on the projection type. The coefficient estimates and the corresponding significance tests are computed for the fitted GLMM using the emtrends function from the emmeans R package.

Number of synapses

N_syn measures the number of synapses between two neurons. We model it as a Poisson-distributed random variable and its relationship to functional similarities as a GLMM model with the following specifications:

where:

• \(N_\rmsyn_ij\) is the number of synapses between presynaptic neuron i and postsynaptic neuron j.

• Sim_ij is the functional similarity between the neuron pair.

• Proj_k(i, j) is the projection type of the neuron pair (i, j).

• β₁, β₂, and β₃ are the fixed effect coefficients of the functional similarity, projection type, and their interaction term, respectively.

• β₀ is the intercept.

• u_k(i, j),i is the random effect accounting for the projection type k and the proofread status associated with presynaptic neuron i.

• ϵ_ij is the error term, following a Poisson distribution.

The coefficients β₁, β₂, and β₃ estimate how the functional similarities and projection types affect connectivity regardless of the spatial scales (axonal or synaptic). We fit the models for each functional similarity independently using the glmmTMB R package. The goodness-of-fit of the estimated models is reported as Nakagawa’s R squared, computed with the performance R package. We define the axonal-scale like-to-like coefficients for each functional similarity and projection type as the estimated linear association between each category of functional similarity conditioned on the projection type. The coefficient estimates and the corresponding significance tests are computed for the fitted GLMM using the emtrends function from the emmeans R package.

Synapse conversion rate

N_syn/L_d measures the number of synapses per millimetre axon–dendrite co-travel distance for each neuron pair. To quantify its relationship to functional similarities, we adopted the following GLMM model:

where:

• \(N_\rmsyn_ij\) is the number of synapses between presynaptic neuron i and postsynaptic neuron j.

• \(L_\rmd_ij\) is the axon–dendrite co-travel distance between the neuron pair.

• Sim_ij is the functional similarity between the neuron pair.

• Proj_m(i, j) is the projection type of the neuron pair (i, j).

• β₁, β₂ and β₃ are the fixed effect coefficients of the functional similarity, projection type and their interaction term, respectively.

• β₀ is the intercept.

• u_k(i, j),i is the random effect accounting for the projection type k and the proofread status associated with presynaptic neuron i.

• ϵ_ij is the error term, following a Poisson distribution.

The above equation can be re-arranged to:

Thus, β₁, β₂ and β₃ model how the functional similarities affect synapse conversion rate (N_syn/L_d) at the synaptic scale. We fit the models for each functional similarity independently using the glmmTMB R package. The goodness-of-fit of the estimated models is reported as Nakagawa’s R squared, computed with the performance R package. We define the like-to-like coefficients of each functional similarity for each projection type as the estimated linear association between each category of functional similarity conditioned on the projection type. The coefficient estimates and the corresponding significance tests are computed for the fitted GLMM using the emtrends function from the emmeans R package. To avoid fitting models to projection types with little data or dominated by few presynaptic neurons, for all the models described above, we only include and report like-to-like coefficients to projection types with more than 30 synapses observed, more than 5 presynaptic neurons, and with none of the presynaptic neurons contributing more than half of all synapses observed.

Statistical analysis of functional similarities and synaptic anatomy

We investigated the relationship between functional similarities of neurons and the anatomical features of their synaptic connections. Our analysis accounted for the confounding effect of axon–dendrite co-travel distance (L_d), which correlates with both functional similarities and synaptic measurements. To isolate the effect of synaptic anatomy on functional similarity, we employed a two-step regression approach:

First, we condition our analysis on the effect of L_d from the functional similarity measure. This process involves:

1. (1)

   Fitting a linear regression model with functional similarity as the dependent variable and L_d as the independent variable.

2. (2)

   Calculating the residuals from this model, which represent the variation in functional similarity that cannot be explained by L_d alone.

These residuals become our new measure of functional similarity, adjusted for the influence of L_d. Next, we constructed a linear regression model using these residuals as the dependent variable. The independent variables in this model included anatomical measurements of synaptic connections, the total number of synapses between neuron pairs and the mean synaptic cleft volume.

This approach allows us to test whether synaptic measurements significantly predict functional similarities between neurons, beyond what can be explained by their physical proximity (as measured by L_d).

Relationship between like-to-like connectivity and somatic distance

To quantify how like-to-like connectivity changes with the physical distance between neuron somas within V1, we measured the 3D EM somatic distances between connected neuron pairs compared to all other unconnected functionally co-registered neuron pairs that shared the same presynaptic neuron population. We then assessed how several measures of functional similarity varied with somatic distance. These measures included in vivo signal correlation, in silico signal correlation, feature weight similarity, and RF centre distance. Somatic distances were binned into 100-μm intervals for this analysis.

RNN model

The RNN model used to produce the results in Fig. 6 consisted of a vanilla RNN layer with 1,000 hidden units and a hyperbolic tangent activation function simulated over 20 time steps. Static inputs were obtained by passing MNIST images through a linear layer. Outputs were obtained by passing the hidden activations at the last time step through another linear layer. All three layers were trained for 10 epochs, a batch size of 512, the categorical cross entropy loss function, and the Adam optimizer in PyTorch. A pre- and postsynaptic neuron pair was classified as connected if the associated weight was in the top 35th percentile of all weights, specifically if the weight larger than 0.01. In Fig. 6d, weights were chosen as candidates for ablation if the weight was above 0.01 and the neurons’ signal correlation was above 0.2. About 10.5% of the weights met these criteria, and ablated weights were selected randomly from this set. Changing the thresholds for weights and signal correlations did not change our conclusions. For several different hyperparameters (number of hidden units, number of time steps, and batch size), we tested sensitivity by varying the hyperparameter across a fourfold range of values. Our overall findings did not change. We also verified that the results are similar when the model is trained on FashionMNIST in place of MNIST.

Common input analysis

Functional similarity among all postsynaptic neurons sharing one common input

For a connectivity graph G, we define

where i is a presynaptic neuron and j, k are any two neurons in the volume. ρ measures the average similarity of all postsynaptic neurons of the presynaptic neuron i.

Estimation of ρ expected by pairwise like-to-like connectivity rules

With the observed connectivity graph G, we estimated the relationship between N_syn and the functional similarities (in silico signal correlation, feature weight similarity and RF centre distance) with GLMM similar to the specifications for modelling the number of synapses described above. Instead of modelling each functional similarity independently, we included all functional similarities and their interaction with projection types in a single model to account for as much pairwise connectivity rule as possible. We then estimated the expected functional similarity among all postsynaptic neurons sharing one common input i as:

where \(N_\rmsyn_ij^\prime \) is the predicted number of synapses between neurons i and j given their functional similarities by the GLMM.

Common input analysis in the RNN model

To replicate the common input analysis in the RNN model, we applied the same methodology described above. We first binarized connections in the RNN model with the same threshold described in the RNN section above. The relationship between connectivity and signal correlations is then modelled as a logistic regression model. The average postsynaptic neuron similarity and the expected similarity is estimated as:

where W_i,j is the binarized weight between artificial neurons i and j.

where P_i,j is the connection probability between artificial neurons i and j predicted by the logistic regression model.

Software

Experiments and analysis are carried out with custom built data pipelines. Our custom data pipeline (https://github.com/cajal/pipeline) is developed in Matlab (2016a, 2018b), Python (3.6, 3.8) and R (4.3.3) with the following tools: PsychToolBox 3, ScanImage (2017b), DeepLabCut (2.0.5), CAIMAN (1.0) and Labview (2016) were used for data collection; DataJoint (0.12.9), MySQL (5.7.37) and CAVE (4.12,4.14,4.16) were used for storing and managing data; Meshparty (1.16), NEURD (1.0.0) and pcg_skel (0.3,0.2) were used for morphology analysis; Numpy (1.23.5), pandas (1.5.3), SciPy (1.10.1), statsmodels (0.13.5), scikit-learn (1.2.1), PyTorch (1.12.1), tidyverse (2.0.0), glmmTMB (1.1.10), performance (0.12.2) and emmeans (1.10.3) were used for model training and statistical analysis; Matplotlib (3.7.0), seaborn (0.12.2), HoloViews (1.15.4), Ipyvolume (0.5.2) and Neuroglancer (https://github.com/seung-lab/neuroglancer) were used for graphical visualization; and Jupyter (ipykernel:6.21.2), Docker (23.0.1) and Kubernetes (1.22.11) were used for code development and deployment.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.