Fully forward mode training for optical neural networks

Experiments

Free-space experimental system

In the free-space FFM system, the light source of the optical computing was generated using a solid-state laser (MFL-FN-532) at a working wavelength of 532 nm. The coherent light wavefront was expanded using a beam expander and then split into two paths by a beam splitter (BS013, Thorlabs). One path was directed towards spatial light modulators (SLMs) for data/error complex field loading, while the other path served as the interference beam with light intensity attenuated by two polarizers (LPNIR100-MP2, Thorlabs). The SLM for field loading (X15213-01, Hamamatsu Photonics) was configured to work in the amplitude modulation mode, which consists of 1280 × 1024 modulation elements with a pitch of 12.5 µm and 8-bit programming depth. It can modulate incident light at a maximum speed of 60 Hz. The amplitude modulated optical field was then 1:1-relayed to the design space SLM (E-Series, Meadowlark Optics) by 4 f system for phase modulation, after polarization adjustment with a half-wave plate and a linear polarizer. The design space SLM was a reflective liquid crystal on silicon device with a high zero-order diffraction efficiency of 91%. It contained 1920 × 1200 modulation elements, each with a size of 8 µm and 8-bit precision, and operated at a maximum frame rate of 60 Hz, with an update time of 17 ms. The phase modulation SLM worked both for electric field loading and design phase loading. The wavefront carrying the input light field and the design phase then probed the symmetry propagation system to perform specific tasks. The output beam was split towards two separate sensors before propagating over a length of 0.388 m. A CMOS sensor (BFS-U3-89S6M, FLIR) was utilized to measure the complex field, with decent quantum efficiency (63.99%) and low dark noise (2.47 e^−). Two sensors were employed to respectively measure the amplitude and phase of the results. The CMOS sensor can achieve a maximum frame rate of 42 Hz with pixel settings of 4096 × 2160, where each pixel has a size of 3.45 µm and the readout values are configured as 8-bit. To measure the complex field, we employed phase-shifting holography, where the phase difference between the reference beam and signal beam is shifted 0,0.5π radian, and 1.0π radian, for the reconstruction of the phase and amplitude of the signal light. A free-space optical system is illustrated in Supplementary Fig. 15. In photon number-limited all-optical NLOS processing, a scientific CMOS sensor Andor Zyla 4.2 with 0.9 e^− read noise and 82% quantum efficiency was used for evaluation. The photon number was controlled with a variable neutral density filter.

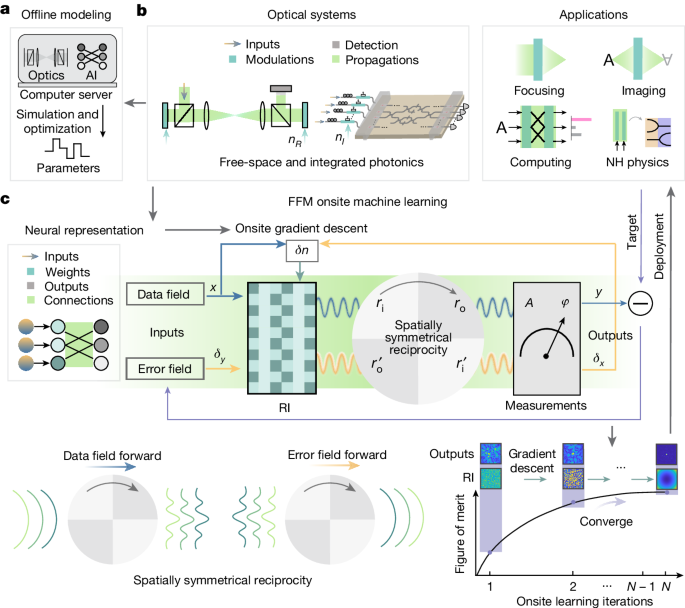
We configured 2/4/6/8 layers of networks, with a propagation distance of 0.388 m for each layer. For imaging through scattering experiment, the distance between the modulator and the scattering medium was 0.194 m, while the distance between the scattering medium and the output sensor was also 0.194 m. The computational operations within each layer of the ONN in section consisted of two stages (Fig. 2a): optical modulation in the design region and fixed free-space propagation. Taking advantage of the symmetry of free-space propagation (indicated by dashed grey lines), the FFM learning method is employed to optimize the effective index of the liquid crystal in the spatial modulators. The liquid crystal is configured in the pure-phase module; hence, the optimization is in essence on the real parts of the effective refractive index n_R. Specifically, in the design process, the data field (shown in blue) undergoes propagation through the physical systems. The resulting outputs from this data propagation are compared with the target outputs to generate error fields (represented in orange). These error fields are then forward propagated through the symmetrical system to obtain error field outputs. Gradients of each designed layer are computed using the data inputs and error outputs. Before FFM learning is conducted, spatially symmetrical reciprocity is validated through a two-step propagation (Supplementary Note 4). The experimental setup illustrated in the bottom panel of Fig. 2a implements layer-by-layer data and error propagation with a 0.388 m propagation distance and 160,000 optical neurons (400 × 400). The complex output light field is probed by interfacing the signal beam with a reference beam, and phase-shifting holography is employed to retrieve the complex light field. The ground truth target was set as the one-hot encoding with the ones designating the right categories. In the error propagation, layer parameters are loaded in reverse order.

For results in Fig. 3, the input wavefront covering an area of 3.2 mm × 3.2 mm was divided into 400 × 400 pixels and concurrently optimized to achieve focused imaging through the scattering media. The designed focal points were subsequently utilized to evaluate point-scanning of an object located beyond the scattering media. The resolution was calculated from \(d=0.5\,\lambda /{\rm{N}}{\rm{A}}\) (ref. ⁴⁸), with NA standing for numerical aperture; see also the illustrations in Supplementary Fig. 11. Two types of scattering media were used in the experiment. The first type was generated using a kilohertz high-speed phase modulator projected with a random phase pattern. The degree of scattering can be adjusted by binning the granularity of the scattering patterns into different sizes. The second type of scattering medium was made of a used scotch tape (Supplementary Fig. 8). In the dynamic parallel NLOS experiment, the distance between the modulator and the objects in the scene, and the distances between the objects and the camera were both 0.194 m. Two different NLOS systems were used in the experiment. For results in Fig. 4b, the input and output light were double reflected by a diffusive reflector, with the ‘T’, ‘H’ and ‘U’ targets placed 0.04 m away (Supplementary Fig. 16). For phase imaging and all-optical processing, to accommodate the large training data number, the diffusive reflector and the targets were projected with another SLM. All the experiments had 8 µm neurons with neuron number of 400 × 400.

Additionally, in Extended Data Fig. 4a, we illustrate the application of FFM learning for imaging phase images with a resolution of 28 × 28. Through FFM learning, the phase targets projected with SLM at the NLOS region are converted into intensity images on the camera at the line-of-sight (LOS) region. Alongside FFM learning, an ANN for image reconstruction (Supplementary Note 7) was trained for the same task, with four handwritten digits employed for learning. At the bottom of Extended Data Fig. 4a, we characterize the structural similarity between the recovered image and the original image under different signal-to-noise ratio levels. With a 15 dB signal-to-noise ratio, FFM learning achieved an SSIM index of 0.81, while the ANN only recovered an image with a 0.40 SSIM similarity. Furthermore, we employed the rotation of the scattering phase around its central point (Supplementary Fig. 14). The system operates at two rotating speeds, denoted as v₁ = 1.0 degrees per iteration and v₂ = 2.5 degrees per iteration. The results are shown in Extended Data Fig. 4b; with the low rotating speed, the in silico ANN eventually converged to the same accuracy as the FFM, albeit requiring a larger number of iterations. As the rotational speed increased from v₁ to v₂, (ν, rotation velocity) the ANN model synchronously degraded with changes in the scattering medium. By contrast, FFM learning continued to advance its accuracy as the learning process evolved.

Integrated photonic experiment system

The integrated photonic chip was tapped out in a commercial silicon photonics foundry. To facilitate an end-to-end incoherent matrix-vector multiplication, the chip realizes a photonic core, incorporating four grating coupler arrays for on- and off-chip optical coupling, 220 nm fully etched strip waveguides for signal routing, four multimode interferometers for optical fan-in and fan-out, and four p–i–n VOAs for weight programming.

The die cores were first diced from the fabricated 8 in. wafer. Then optical inputs and outputs (I/Os) were packaged with fibre arrays and electrical input pads were bonded off-chip to a dedicated printed circuit board. The chip under the packaging was shown in Fig. 5b. Details of the packaging methods are also described in Supplementary Note 6. After packaging, in the integrated photonic experiment system, as illustrated in Extended Data Fig. 3, two lasers with output powers of 10 dBm were utilized as two-channel input sources. For incoherent matrix operations, one laser operated at a precise wavelength of 1,550 nm, while the other operated at 1,551 nm. The polarization of light within the fibre was adjusted using polarization controllers, ensuring its alignment with the transverse electric coupling mode of the grating coupler. Following the polarization control, two microelectron-mechanical-systems variable optical attenuators (V1550A, Thorlabs) were employed to encode the input signal and the weight of the imaginary refractive index. The outputs of the variable optical attenuators were then coupled into the photonic chip through fibre arrays. On the chip, four p–i–n VOAs controlled by an arbitrary waveform generator attenuated the fanned-out two-channel input light, and fanned-in the signal into two separate output paths. The attenuated light was subsequently coupled off-chip and detected by 5 GHz photodiodes with around 1.0 A/W calibrated photoresponsivity over the 1,500–1,600 nm optical band. The captured photocurrents were amplified with transimpedance amplifiers (AMP100, Thorlabs) of 100 kΩ transimpedance, and the amplified output voltage signals were finally measured and read out by a multichannel oscilloscope.

This network presented in the main text comprises five layers with neuron counts of 16, 16, 16, 8 and 8, respectively, from the first to the last layer. Within each layer, input data are partitioned into pairs, each containing two elements. These input pairs are encoded using mutually incoherent wavelengths and passed through the symmetrical cores. The resulting outputs are detected using high-speed photodiodes, where the mutually incoherent signals are added together. Consequently, each core performs a matrix-vector multiplication operation. To facilitate interlayer connections, the outputs of the neurons are shuffled before being connected to the subsequent layer.

The FFM learning procedure

In both free-space and integrated systems, FFM learning unfolds sequentially into four steps: data propagation, final loss calculation, error propagation and gradient calculation. As elaborated in Supplementary Note 5, the complete FFM learning protocol entails a synergy between optical and electronic systems, with compute-intensive propagations executed on site. On the electronic front, it oversees optoelectronic nonlinear activation between layers, final loss and gradient calculation, and input data loading. Furthermore, we have confirmed that loss and gradients can be computed using onsite optics and electronics, as outlined in Supplementary Note 13. Additionally, the nonlinear function can be realized entirely optically or optoelectronically without the need for digital electronics.

Dataset preparation

MNIST dataset

The MNIST dataset⁴⁹ is a collection of ten-category handwritten digits, comprising 60,000 training samples and 10,000 testing samples. Each original sample was converted into an image with a resolution of 392 × 392 and then zero-padded to a resolution of 400 × 400. In the multilayer classification experiment, each sample in the ten categories was utilized to construct the input complex field with a phase set to zero. In the NLOS tasks, the samples were treated as invisible objects and modelled as a phase-only mask for the imaging and classification.

Fashion-MNIST dataset

The Fashion-MNIST dataset⁵⁰ comprises fashion products of ten different categories, consisting of a training set with 60,000 samples and a test set with 10,000 samples. Each original sample was transformed into an image with a resolution of 392 × 392 and then padded to a resolution of 400 × 400. In the multilayer classification experiment, each sample was used to create the input complex field with a phase set to zero.

CIFAR-10 dataset

The CIFAR-10 dataset⁵¹ is a subset of the 80 million tiny images dataset, containing 50,000 training images and 10,000 test images. Each original sample was converted into a greyscale image and resized to a resolution of 400 × 400. In the multilayer classification experiment, each sample was used to construct the input complex field with a phase set to zero.

ImageNet dataset

The ImageNet dataset⁵² is an image database organized according to the WordNet hierarchy, in which each node of the hierarchy is depicted by hundreds and thousands of images and in total there are 120 million images for training and 50,000 images for testing. Each original sample was converted into a greyscale image and resized to a resolution of 400 × 400. In the multilayer classification experiment, each sample was used to construct the input complex field with phase values set to zero.

MWD dataset

The MWD dataset⁵³ comprises weather condition images of four different outdoor scenes: sunrise, shine, rain and cloudy. It contains a total of 1,125 samples, with 800 samples used for training and 325 samples for testing. Each original sample is converted into a greyscale image with a resolution of 400 × 400. In the multilayer classification experiment, these greyscale images were utilized to construct the input complex field, with the phase set to zero for all samples.

Iris dataset

The Iris dataset⁵⁴ consists of three Iris species, with 50 samples for each species, along with several properties describing each flower. One of the flower species is linearly separable from the other two, while the other two species are not linearly separable from each other. For our experiment, we used 120 samples, with 40 samples from each species, for training, and 30 samples for testing. Each original sample in the dataset contains four entries that describe the shape of the Iris species. In the PIC experiment, each entry was duplicated to create four identical data points, resulting in a total of 16-channel input data.

Chromium target dataset

The real scene dataset is specifically designed for NLOS scenarios involving real-world objects. It consists of glass chrome plates with distinct regions: reflective and translucent. The reflective areas represent the physical scene itself (letter targets ‘T’, ‘H’ and ‘U’). During the training process, a single reflective area is used, and it is systematically moved within the same plane to generate nine different training scenes. The test data consist of three letters composed of multiple reflective areas. During testing, the scene plate was translated with motor stage to position different letters within the illuminated regions.

Embedded photonic neural network architecture

Free-space neural network

The input data \(X\in {C}^{\mathrm{160,000}}\); the input is per-point weighted by designed complex weight \(M\in {C}^{\mathrm{160,000}}\) and propagated to the outputs. Denote the propagation matrix as \(T\in {C}^{\mathrm{160,000}\times \mathrm{160,000}}\); each layer propagation is \(Y=T(M\cdot X)\). In the deep free-space neural network, the network model is \(Y=({\Pi }_{i=1}^{L}{T}_{i}{M}_{i})X\), where L is the total number of layers. In imaging through scattering media, Y = TSTMX, where S represents the transportation of the scattering media. In the NLOS imaging system, \(Y={TR}_{{\rm{ref}}}T{R}_{{\rm{ob}}}T{R}_{{\rm{ref}}}TMX\), where R_ob represents the NLOS object reflectance and R_ref represents the reflector (refer to Supplementary Note 3 for derivation of symmetry in transportation matrices).

The loss function used in the free-space neural networks is the mean squared error (MSE) loss, which calculates the average squared difference between the predicted outputs and the ground truth. In classification tasks in deep ONNs, for Fig. 2c,d, we respectively used 60,000, 60,000, 30,000 and 800 samples for training, and 10,000, 10,000, 5,000 and 325 samples for testing when using the MNIST, CIFAR-10, Fashion-MNIST and MWD datasets. For Fig. 2f,g, we used 10,000, 8,000 and 5,200 samples for training, and 500, 200 and 200 samples for testing, on MNIST (categories ‘0’, ‘2’, ‘4’, ‘6’, ‘8’), CIFAR (categories ‘automobile’, ‘dog’, ‘frog’ and ‘horse’) and ImageNet (categories ‘tabby’, ‘basketball’, ‘castle’ and ‘envelope’). The targets were configured as binary images where the maximal values are normalized to 1.0 in the detected regions corresponding to the respective categories and 0 in the remaining regions. The MSE loss was employed to measure the discrepancy between the intensity of the output diffraction field and the desired target. When calculating testing accuracy, we tested five times for each experiment and got the mean value of the convergence results. In high-resolution imaging systems, the focusing target was a binary image with a value of 1.0 in the central region of the image, with a diameter of 10 pixels and 0 in the surrounding regions. The intensity of the output field was compared with the desired target to compute the MSE loss. In parallel dynamic NLOS imaging and processing systems, the target for the 3 × 3 square grid array imaging was a binary image with a value of 1.0 (high reflectance) in specific regions of the grid that formed letters such as ‘T’, ‘H’ or ‘U’. In high-resolution phase imaging, the target is obtained by binarizing greyscale images of the object to be detected. For phase object imaging, we selected objects from four different categories—‘0’, ‘2’, ‘7’ and ‘9’—of the MNIST dataset and mapped the pixel values to phase range 0–π. The output targets were the original intensity images. For the phase object classification task in NLOS system, we used two categories, ‘0’ and ‘7’, from the MNIST dataset, 2,000 samples for training and 200 samples for testing. The targets were one-hot vectors similar to those used in deep optical neural networks. The MSE loss was employed to quantify the discrepancy between the predicted intensity outputs and the desired targets for the imaging and classification experiments. The optimizer used to optimize the parameters of free-space neural networks is the Adam optimizer⁵⁵, which incorporates exponentially weighted averaging and accelerates gradient descent.

PIC network

In the PIC network, the 16-channel input \({x}_{0}=[{x}_{1},{x}_{2},\ldots ,{x}_{16}]\) is multiplied by a 16-channel modulation mask M₁ and the results are connected to the next layer through a local 2 × 2 matrix. In the 16-channel output \({y}_{1}=[\,{y}_{1},{y}_{2},\ldots ,{y}_{16}]\), each adjacent pair of outputs \([\,{y}_{2n-1},{y}_{2n}]\,(n=\mathrm{1,2},\ldots ,8)\) is only related to the corresponding pair of inputs \([{x}_{2n-1},{x}_{2n}]\), which can be calculated by \(\left[\begin{array}{c}{y}_{2n-1}\\ {y}_{2n}\end{array}\right]=\left[\begin{array}{cc}{w}_{n1} & {w}_{n2}\\ {w}_{n3} & {w}_{n4}\end{array}\right]\left[\begin{array}{c}{x}_{2n-1}\\ {x}_{2n}\end{array}\right]\). The \({w}_{n2},{w}_{n3}\) of the modulation mask are the same to satisfy the symmetry condition. Afterwards, the 16-channel output undergoes a specific shuffling process. The output is rearranged according to a predetermined table: T_1 = [0,2,1,3,4,6,5,7,8,10,9,11,12,14,13,15] and the resulting arrangement determines the 16-channel input for the next layer by \({x}_{1}[i]={y}_{1}[{T}_{1}[i]]\,(i=\mathrm{1,2},\ldots ,16)\). Layer 2 follows a similar structure as the first layer, and the shuffling table for the output is defined as T_2 = [0,4,8,12, 1,5,9,13, 2,6,10,14, 3,7,11,15]. Accordingly, layer 3 transforms the modulated 16-channel input into an 8-channel output by summing adjacent channel inputs \(\left[{x}_{2n-1},{x}_{2n}\right]\) to obtain a single output channel, y_n. Then the output is shuffled based on another predefined table T_3 = [0,2,1,3, 4,6,5,7]. Layer 4 is similar to the first layer but has only eight channels, and a new shuffling table is used: T_4 = [0,4, 1,5, 2,6, 3,7]. The last layer, similar to layer 3, converts the modulated eight-channel input into a four-channel output. The final output is used to determine the category corresponding to the input data. The network architecture is visualized in Supplementary Fig. 16.

The loss function of a photonic integrated neural network is cross-entropy loss, which aims to minimize the difference between the predicted probability distribution and the true probability distribution. It can be calculated in the following way:

with given final output probability distribution y₅, the target label gt, the number of training samples N, and the number of categories K. In a photonic integrated neural network, the output is the magnitude of the voltage signal received from the oscilloscope and the target is the label of the input data. The dataset contains 120 training samples and 30 testing samples in total. Cross-entropy loss is used to measure the difference between the output and the target, and the loss is optimized with an Adam optimizer.

Self-designing non-Hermitian system

Traditionally, the study of exceptional points in a non-Hermitian system requires numerically solving an a priori model⁵⁶. Here we numerically demonstrate that the FFM can self-design non-Hermitian traversing over the exceptional point without resorting to physical models. As shown in Extended Data Fig. 1, we study the wave propagation in symmetrical dual waveguides, where one waveguide is for the gain and the other for the loss. In the case studied, while we can probe the system by feeding in optical signals, we do not explicitly know the formulation of the Hamiltonian. To design the gain and loss, we use as a target the breaking of the lateral reciprocity of the system, that is, control the asymmetry of the output signal by feeding input to symmetrical channels but maximize the output of one waveguide (Supplementary Note 8). It was observed that with FFM learning, the system output could switch from a reciprocal to a nonreciprocal regime, or vice versa. When comparing with the knowledge of non-Hermitian optics, we discovered that the switching guided by FFM self-design was accompanied with the spontaneous parity-time symmetry-breaking, and the learning process corresponded to the non-Hermitian braiding group \({{\mathbb{B}}}_{2}\). The FFM design provides a target-oriented way to solve complex topological systems.

Comparison with state-of-the-art high-performance optical systems

Deep ONNs

Realizing neural networks with deeper layers and a larger scale is of vital importance for optical computing to gain higher performances. As shown in Extended Data Table 1, the depth of reconfigurable optical neural networks reported in previous works is at most five for free-space neural networks and three for PICs^{17,18,19,24,34,38}. Further increasing the network depth would cause error accumulation and degrades the performances of the neural networks²⁴. The FFM onsite machine learning method alleviates the necessity of a numerical model, and thus is without the issues of imprecise modelling. Accordingly, FFM learning achieved ONNs with a depth of at least eight for free-space neural networks with millions of parameters, and reached a depth of five for integrated photonic circuits. During FFM learning, the network performances stably increase. A more detailed discussion on emerging neural network training methods^57,58 is presented in Supplementary Note 10.

Focusing through scattering media

Focusing through scattering media with high precision has applications in microscopic as well as macroscopic imaging^59,60. Existing focusing through scattering methods relies on optimization with feedback, which is not optimal and is slow to converge⁶¹. FFM learning transforms the focusing system into a target-oriented onsite neural network and learns to focus with gradient descent. Our results reach the theoretical limit of optical resolution.

NLOS scene imaging and processing

NLOS is a difficult scenario whereby objects are hidden beyond the line of sight. As shown in Extended Data Table 2, due to the lack of direct photons, imaging is challenging in NLOS and requires dedicated scanning such that the speed is usually limited to seconds to minutes per frame^62,63,64. FFM learning inherently models the highly diffusive propagation into part of the imaging system, and enables parallel imaging of the object at a single shot. Our system demonstrates 1 ms exposure time, but the speed can be further accelerated with high-speed cameras. FFM learning can also transform the NLOS propagation into part of the onsite processing system, so that the hidden object can be all-optically processed with as few as <1 photon per pixel.

Exceptional point searching

FFM learning supports analysis of the topological photonics system on site. We achieved results on a non-Hermitian system that agreed well with the theoretical analysis. Previous studies needed to first model the system offline and carefully approach the theoretical results on site by carefully tuning the gain and loss^56,65,66,67. Our findings show that the symmetry-breaking of the non-Hermitian system can also be realized on site without careful offline modelling, which presents a new way to study optics and may help in designing topological systems of larger scale and higher order.