Fluctuating DNA methylation tracks cancer evolution at clinical scale

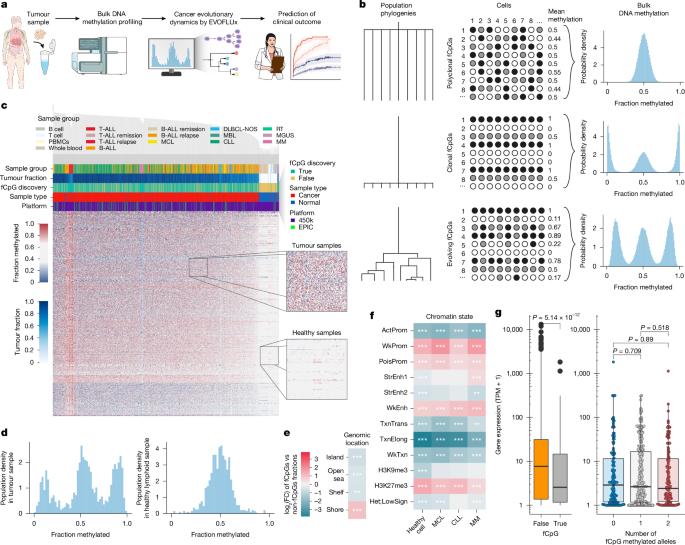
Assembly and quality control of DNA methylation data

We assembled and processed with a harmonized pipeline¹⁴ (v4.1; see Code availability section) 2,430 bulk sample Illumina methylation array data of normal and neoplastic lymphoid cells from previous publications^{14,21,22,23,24,25,26,27,28,29,30}. As healthy control samples, this dataset contained sorted CD19⁺ B cells (n = 40), CD3⁺ T cells (n = 35), peripheral blood mononuclear cells (n = 6) and whole-blood samples (n = 6). As tumour samples, we included precursor 797 B-ALLs and 90 T-ALLs at diagnosis, 28 B-ALLs and 2 T-ALLs at relapse, as well as 74 B-ALLs and 12 T-ALLs at complete remission (that is, normal blood); 149 MCLs; 722 CLLs, 55 of its precursor condition MBL and 6 samples from patients with CLL undergoing a DLBCL transformation called Richter transformation; 62 primary DLBCL, not otherwise specified; and 104 multiple myeloma and 16 of its precursor condition monoclonal gammopathy of undetermined significance. In brief, raw idat files were loaded and processed with R (v4.3.1) using the minfi package^50,51 (v1.46.0) in batches as specified in the column ‘SSNOB_NORMALIZATION_BATCH’ of Supplementary Table 2. In brief, the data were processed for each batch as follows. First, idats files were loaded into a RGChannelSet object, and minfi quality metrics using the qcReport function were performed, removing samples with unexpected distributions of methylation values (that is, distributions markedly distinct from a bimodal centred around 0 and 1 β-values and/or from the remaining samples) and low signal intensities of internal control probes for each sample, including bisulfite conversions I and II, extension hybridization, hybridization, non-polymorphic, specificities I and II, and target removal probes.

Next, further quality metrics were derived using the function minfiQC on the unnormalized RGChannelSet obejct. Those samples with median signal intensities of unmethylated and methylated channels of at least 10.5 in log₂ scale were considered as having good signal intensities. Subsequently, detection P values were calculated across all CpGs and samples using the detectionP function for the unnormalized RGChannelSet object. Samples were considered as good if having a mean detection P value across all CpGs of P ≤ 0.01. On a CpG level, we retained CpGs with a detection P ≤ 1 × 10⁻¹⁶ in 90% or more of the samples, which has been shown to improve the quality of downstream analyses^52,53. The RGChannelSet object was normalized with the single-sample batch-independent preprocessNoob function with dye bias correction. We next retained only CpGs (excluding CH probes) that did not contain any SNP neither in the interrogated CpGs nor in the probe extension using the dropMethylationLoci and dropLociWithSnps functions with default options (minor allele frequency (MAF) = 0). Further analyses using long-read nanopore data, Illumina array control probes, annotation packages and a data-driven approach were used to ensure the lack of any genetic confounding in the methylation values of the resulting fCpGs (see the next sections).

Furthermore, CpGs with any previous evidence of potential cross-hybridization were excluded⁵⁴ and only CpGs mapping to autosomal chromosomes were subsequently retained for downstream analyses. Finally, to further confirm the accuracy of the filtering criteria, we checked the distribution of normalized methylation values and performed principal component analyses separately for samples passing all quality checks as well as those considered as bad samples. The final DNA methylation matrix contained 2,204 samples and 389,180 CpGs passing all the aforementioned quality controls, and included 2,054 patients (22 technical replicates, 3 synchronic and 125 longitudinal samples from the same patients)⁵⁵ (Supplementary Table 2).

To determine the purity of samples, we used our previously deconvolution strategy to infer tumour cell content by DNA methylation¹⁴, which was used as a consensus purity in all the tumour samples except for DLBCL and multiple myeloma. In these two tumour entities, we have previously identified a DNA methylation signature loss causing inaccurate tumour purity predictions using DNA methylation data, and therefore we used available genetic or flow cytometry data for DLBCL and multiple myeloma, respectively.

Pipeline to select fluctuating CpGs

We constructed a pipeline to identify fCpGs in lymphoid tumours, based on the following criteria:

1. (1)

   Heterogeneous across different participants with the same disease (by accepting CpG loci with the top 5% of standard deviation of methylation value within a cancer type).

2. (2)

   Equally likely to be methylated or unmethylated (by selecting CpGs with average methylation of approximately 0.5 within a cancer type).

3. (3)

   Unlikely to be associated with specific cell or cancer types. We used an unsupervised Laplacian score feature selection metric⁵⁶ to rank CpG loci by their tendency to preserve the nearest-neighbour graph, and accepted the 5% least-informative CpGs.

Exclusion of genetic confounding on fCpGs

We performed a series of analyses to exclude the potential genetic confounding (germline SNPs and somatic SNVs) on our fCpGs. We first excluded the possibility that common germline SNPs caused methylation heterogeneity at fCpG sites between individuals. We observed very distinct methylation dynamics of array control probes containing SNPs (which had been removed during the initial array processing) versus fCpGs. SNP probes showed the same distribution in all samples (Extended Data Fig. 2c), including longitudinally followed cases (Supplementary Fig. 3), whereas fCpGs only showed a W distribution in cancer samples with ongoing fluctuations over time. Thus, although SNPs reflect the stable genetic identity of the individual, fCpGs reflect the identity of a single cell and its evolving lineage. In addition, we used the packages SNPlocs.Hsapiens.dbSNP155.GRCh38 (v0.99.24) and MafH5.gnomAD.v4.0.GRCh38 (v3.19) to check for any known significant germline or somatic genetic confounding on the resulting 978 fCpGs. We found approximately 60% of fCpGs reported in the gnomAD v4 database (with the array background having approximately 65%), but with a very low MAF (median of 1 × 10⁻⁵ and mean of 1 × 10⁻³). To exclude the possibility of unknown or very rare genetic confounding, we used the data-driven gaphunting algorithm⁵⁷ available in the minfi R package, which further discarded a possible cancer-specific single-nucleotide variation (SNV) that could confound the methylation values at the 978 identified fCpGs. Finally, Oxford Nanopore long read of a subset of normal and neoplastic samples further validated that fCpGs represent de/methylated cytosines (Extended Data Fig. 2d,e; see next section).

Generation and analyses of long-read nanopore data

For long-read methylation sequencing in CLL and Richter transformation samples, concentration was assessed using the Qubit assay and DNA integrity was analysed either with the Femto Pulse System (Agilent) or the Fragment Analyzer (Agilent). When more than 6 µg of material with good integrity was available, DNA was additionally treated with the Short Fragment Eliminator Kit XS (PacBio) and eluted in EB buffer. Approximately 4 µg of DNA was used for library preparation according to the standard LSK114 kit and protocol from Oxford Nanopore. The time for DNA repair and end-prep was increased up to 30 min at 20 °C and 30 min at 65 °C. Adapter ligation was performed for 1 h at room temperature. All elutions were performed at 37 °C for 1.5 h, and 550–600 ng of DNA was loaded onto a FLO-PRO114M (CLL cells) flow cells. Flow cells were washed (EXP-WSH004) after 1–2 days, if pore count decreased to less than 30%. A total of 1–4 washes were performed for each flow cell. Flow cells were run for 100 (CLL cells) hours in total with the Fast model (MinKNOW 23.11.7, Dorado 7.2.13). The raw data were rebasecalled using dorado duplex (v0.5.3) and applying the SUP and modified call to detect 5mC and 5hmC, (model [email protected]_5mCG_5hmCG@v1).

In normal B cell samples, 1–3 µg of DNA was used for WGS. Libraries were prepared with the DNA ligation kit LSK110 with no modifications. Libraries were loaded onto a flow cell version FLO-PRO002 (R9.4) and were run for 90–110 h. The basecalling was performed on live mode with the Guppy basecaller (v6.2.7), included in the MinKNOW (v22.08.6), using the SUP model for base modification detection of 5mC and 5hmC (dna_r9.4.1_450bps_modbases_5hmc_5mc_cg_sup.cfg).

In all samples, the generated unmapped BAM files after the basecalling were converted to FASTQ files using the SAMtools fastq -T Mm, Ml command. The FASTQ files were then mapped to BAM files using the command minimap2 -ax map-ont -y../GCA_000001405.15_GRCh38_no_alt_analysis_set.fna.mmi. The methylation values were extracted from the BAMs into bedMethyl files using the in-house tool bam2bedmethyl (v0.3.2) and compressed/indexed using bgzip/tabix. Reads from each strand were combined to generate DNA matrices for each CpG and were used for obtaining the methylation values of all fCpGs.

In addition, mini BAM files containing all reads from the 976 fCpGs were generated (in hg38 genome assembly). The reads showed excellent mappability, with a mean of perfect nucleotide matches (NM tag; Levenshtein distance) for all fCpGs across samples of 96.41% (range of 73.31–97.90), and mean mapping quality (MAPQ) of all the reads covering all fCpGs across samples of 59.510 (range of 2–60). Subsequently, long reads were phased using variants called using Clair 3 (v1.0.9, model r941_prom_hac_g360 + g422)⁵⁸ with the Longphase package (v1.7)⁵⁹. The methylation status of each CpG was called using the modcall function within the Longphase package. At fCpGs, only 2.7% of the reads were non-canonical bases (Extended Data Fig. 2d). The variant allele frequency (VAF) of these mutations tended to be low and was negatively correlated with the coverage at that site (Supplementary Fig. 4a). Hence, the majority of these non-canonical base pairs are probably due to errors in nucleotide assignment. There is also no association between the methylation status of different reads and the variants present within a 50-bp window of each fCpG locus (Supplementary Fig. 4b). Hence, assessment of fCpG methylation via bead array was not majorly confounded by miscalled variants. The fCpG methylation patterns seen in the bead array data were replicated in the long-read data (Extended Data Fig. 2e) and the correlation between the fraction methylated measured via bead array and long-read sequencing at fCpGs was excellent (Extended Data Fig. 2e). The same correspondence was observed in WGBS data (Extended Data Fig. 2f).

To assess the intra-sample long-read diversity for each sample, the pairwise Hamming distances were calculated between every read on both haplotypes. The two lists of Hamming distances were concatenated, and the mean calculated as a summary statistic of the read diversity for each sample. One normal B cell sample contained only two reads from one haplotype, and zero from the other, and so was excluded from further analysis.

Analysis of scRRBS data

Previously published single-cell reduced representation bisulfite sequencing (scRRBS) data were obtained⁶ and the fCpG methylation values extracted methylation values for normal B cells from 6 donors and CLL cells from 12 patients. There was a high dropout rate, so to extract meaningful patterns we plotted a subset of 40 cells and 20 fCpGs with a high density and overlap of fCpGs across single cells as examples (Supplementary Fig. 5a,b).

To compare the full set of data accounting for the high degree of missing data, we used a metric of heterogeneity at a given fCpG that weights by the number of non-missing fCpGs according to:

Where n_i is the number of non-NaN values for the ith fCpG, \(\frac{n(n-1)}{2}\) is the total possible pairwise comparisons between a set of n objects and σ(β_i) is the standard deviation across the methylation values of the ith fCpG (Supplementary Fig. 5c).

Characterization and annotation of fCpGs

To characterize the genomic and regulatory context of fCpGs, we used a series of statistical analyses and database annotations. We annotated fCpGs using Illumina manifest and other genomic annotation packages available at Bioconductor including IlluminaHumanMethylation450kanno.ilmn12.hg19 (v0.6.1) and IlluminaHumanMethylationEPICanno.ilm10b2.hg19 (v0.6.0). We additionally used the packages SNPlocs.Hsapiens.dbSNP155.GRCh38 (v0.99.24) and MafH5.gnomAD.v4.0.GRCh38 (v3.19) to check any possible germline or somatic genetic confounding on the resulting 978 fCpGs. We found approximately 60% of fCpGs reported in the gnomAD v4 database (with the array background having approximately 65%), but with a very low MAF (median of 1 × 10⁻⁵ and mean of 1 × 10⁻³). In addition, we used the Illumina 450k and EPIC array internal SNP probes and showed a dramatically distinct methylation dynamics compared with fCpGs in single-timepoint (Extended Data Fig. 2c) and longitudinal (Supplementary Fig. 3) samples. Finally, the data-driven gaphunting algorithm available in the minfi R package was applied with all the previously published thresholds and cut-offs⁵⁷, which further discarded possible cancer-specific SNV that could confound the methylation values at the 978 identified fCpGs.

We used Chi-squared tests to assess the enrichment of fCpGs in distinct genomic regions or elements. We performed gene-set enrichment analysis on the fCpG-associated genes using gProfiler⁶⁰, specifically focusing on the Gene Ontology biological processes⁶¹ and the Human Protein Atlas⁶². The statistical domain space was limited to genes targeted by at least one CpG in the 389,180 candidate CpG set and significance was determined using the g:SCS algorithm⁶³. Previous chromatin segmentation of normal and neoplastic B cells was used to assess the chromatin-state enrichment of fCpG^14,64.

fCpGs were checked for their overlap with previous ‘epigenetic clocks’, including mitotic^{14,65,66,67,68}, chronological age^{69,70,71,72,73,74,75,76,77,78}, gestational age^{79,80,81,82,83}, biological age and mortality^84,85,86 and trait predictors^87,88. The package methylCIPHER (https://github.com/MorganLevineLab/methylCIPHER) was used to obtain the CpGs for most of the epigenetic clocks. The package methylclock (v1.10.0) was used to calculate all epigenetic clocks but epiCMIT, which was derived as previously described¹⁴.

CLL RNA sequencing data

Previously available RNA sequencing data for 294 patients with CLL were obtained³³ and processed as previously described²⁶. Matched RNA sequencing data and DNA methylation data for the same patients at the same timepoint were available for 224 patients with CLL. Transcript per million counts were used to represent differential gene expression values across genes and samples. We used the gene annotation provided in the R Bioconductor package IlluminaHumanMethylationEPICanno.ilm10b2.hg19 to classify genes associated with fCpGs. Genes targeted by any fCpG were considered as ‘fCpG genes’.

In each methylation sample, the 978 fCpGs were discretized as homozygous demethylated, heterozygous methylated or homozygous methylated (coded as [0,1,2], respectively). This was done by separately fitting a β-mixture model with three components to each sample using Stan⁸⁹ and extracting the component mixture probability. The gene expression value for genes classified as having and fCpG with 0, 1 or 2 alleles methylated were plotted as previously described.

DNA methylation data from normal blood samples

External DNA methylation data were download from the Gene Expression Omnibus database using the GEOquery R package (v2.72.0). For sorted immune cells, these include GSE137594 and GSE184269. For whole-blood samples, these include GSE72773, GSE55763, GSE40279 and GSE36054. Data were analysed with the normalization procedure used in each study together with the metadata provided. Mean and standard deviation for fCpGs were calculated with fCpGs present in the provided normalized matrices.

A stochastic model of fCpGs in a growing population

We built a generative computational model of how the patterns of fCpGs vary over time (t) according to the evolutionary history of a cancer. Initially, our model focused on neutral evolution, before expanding to non-neutral modes of tumour evolution below. For the full explanation of the model, see the Supplementary Information.

Our model was parameterized in terms of the age of the patient at which the MRCA emerged (τ), the exponential growth rate of the cancer (θ) and the epigenetic switching rates of the fCpGs (μ, ν, γ and ζ). The model was partitioned into two phases: before and after the emergence of the MRCA. At time t = 0, the fCpGs were assumed to be equally likely to be homozygously methylated or demethylated. The fCpG status of the MRCA at time t = τ was calculated by applying matrix exponentiation.

The second phase of the model consisted of a discrete time Markov process. The effective population size of the growing cancer was modelled as growing according to a deterministic exponential growth equation, N_e = e^{θ(T − τ)}. Each fCpG was considered independently; at each time step, t → t + δt, the number of homozygous-methylated (m), heterozygous-methylated (k) and homozygous-demethylated cells (w) at a specific fCpG was updated according to the epigenetic switching rates.

At the time of sample, T, the fraction methylation of each simulated fCpG was calculated by summing the number of methylated alleles and normalizing by the total number of alleles in the population:

We further accounted for contaminating normal cells and the technical noise introduced by the methylation bead array. The methylation of the contaminated samples was assumed to be an average of the cancer methylation, β_c(t), weighted by the tumour purity ρ, and the average of the normal population, β_n, weighted by 1 − ρ. Following our previous work, the bead array was assumed to saturate at extreme methylation values, shifting the minimum and maximum methylation by δ and ε, respectively⁴. The noise of the bead array was assumed to be β-distributed, with precision parameter κ.

Non-neutral models of tumour evolution

Alongside our model of neutral exponentially growing cancer populations, we devised two alternative models of cancer growth:

1. (1)

   A subclonal selection model in which a single cell within the cancer develops a selective advantage and begins to grow at an increased growth rate.

2. (2)

   An independent clonal origins model, in which a patient has developed two distinct cancers concurrently.

For the subclonal selection model, we replaced the growth rate (θ) and the time of the MRCA (τ) with the growth rates and time of the MRCA of the initial, slower-growing population (θ₁ and τ₁, respectively), and that of the more recently emerging, faster-growing population (θ₂ and τ₂), constraining τ₁ < τ₂ and θ₁ < θ₂ (Extended Data Fig. 8a). We assumed that the initial cancer population began exponentially growing at τ₁ as above, but at time t = τ₂, we selected a single cell with a set of fCpG states drawn according to the cancer population and allowed this second population to grow concurrently with a growth rate θ₂.

The independent-cancer model followed the same scheme as the nested subclonal selection model, except the methylation status of the emerging cancer was that of an independent cell that experienced random fluctuations between t = 0 and t = τ₂.

If we let the number of cells in the less fit subclone in each methylation state be {m₁, k₁, w₁} and in the fitter subclone be {m₂, k₂, w₂}, following the convention above, then in both cases the measured methylation patterns at the time of sample are:

Where \({N}_{e}(T)={e}^{{\theta }_{1}(T-{\tau }_{1})}+{e}^{{\theta }_{2}(T-{\tau }_{2})}\).

Adaption of simulations to a longitudinal setting

We modified the simulations of how the fCpG methylation distribution changes over time to allow for multiple sequential sample collections. These simulations allow for neutral, independent clones, a single subclonal expansion or two subclonal expansions, which can either be nested or emerge from the clonal trunk in parallel. This required pre-specification of sampling times, along with the emergence times of any subclones or independent clones, which we collected to form a set of ‘landmark times’. The discrete time steps of the simulation were split into phases between the landmark times, which evolved according to the discrete time Markov process outlined above. At each sampling time, the fCpG methylation fraction was calculated as above and stored as a column in the output matrix.

Prior functions

For each methylation array blood sample, we had matched age (T) and purity (ρ) information. Hence, the parameters to be inferred are the growth rate (θ), the age of the patient when the MRCA emerged (τ), the epigenetic switching rates (μ, ν, γ, ζ), the average fraction methylated of contaminating normal cells (β_n), the β-offsets from 0 and 1 due to the background noise on the methylation array (δ and ε, respectively) and the precision of the β-distributed noise (κ).

These parameters are constrained either to be positive (θ, μ, ν, γ, ζ, κ > 0) or to lie within a specified range (0 < τ/T, δ, ε < 1), which we achieved using appropriate prior distributions. To better allow for priors to be set on a biologically meaningful scale, the priors for the log-normal distribution were set in terms of the real scale mean and standard deviation, rather than the standard log-scale. To reduce correlations in the posterior and make sampling more efficient, the variables ν and ζ were normalized by μ and γ, respectively.

The priors are as follows:

When fitting non-neutral models of tumour growth, the inference was parameterized in terms of the relative growth of the fitter subclone, \({\tilde{\theta }}_{2}=\frac{{\theta }_{2}}{{\theta }_{1}}\), and the fraction of the population consisting of the fitter subclone, \(f=\frac{{e}^{{\theta }_{2}(t-{\tau }_{2})}}{{e}^{{\theta }_{1}(t-{\tau }_{1})}+{e}^{{\theta }_{2}(t-{\tau }_{2})}}\). The age at which the second clone emerges is then:

This parameterization induces less correlation in the resulting posterior, which greatly improves the sampling efficiency. The priors on these additional parameters are:

All the other priors were the same as in the neutral case.

Bayesian inference

We developed a stochastic estimator of the log-likelihood function at a given set of parameters by simulating the fCpG methylation distribution a large number of times, correcting for the bias inherent with using a finite number of simulations and penalizing the log-likelihood for extreme values of the N_e (see Supplementary Information for details).

The standard Bayesian algorithms developed to infer the posterior for a given set of data (for example, Markov chain Monte Carlo (MCMC), nested sampling) are typically used when the log-likelihood is analytically tractable and can be calculated exactly. It has been shown that, as long as the stochastic approximation of the log-likelihood is unbiased, MCMC methods can obtain an exact Bayesian inference of the true posterior, as in pseudo-marginal Metropolis–Hastings⁹⁰.

Here we used a nested sampling approach using the dynesty package^91,92,93. Unlike pseudo-marginal Metropolis–Hastings, nested sampling is able to efficiently explore multimodal posterior landscapes (which can occur under the subclonal and independent cancer models).

Model selection for the mode of tumour evolution

We used an expected log pointwise predictive density⁹⁴ approach to compare our competing models of evolution for each sample using the arviz Python package⁹⁵, which uses PSIS-LOO-CV to compare the out-of-sample prediction accuracy between models while naturally penalizing more complex models. This required the log-likelihood per data point and the posterior predictive for every point in the posterior. The weights of the respective models were calculated using pseudo-Bayesian model averaging using Akaike-type weighting, stabilized using the Bayesian bootstrap⁹⁶.

CLL and Richter transformation genomic analyses

Previous mutated annotation files from WES⁴⁶ and WGS²⁷ data were used to further validate our distinct EVOFLUx evolutionary modes (that is, neutral, subclonal and independent) and Richter transformation phylogenies.

Subclonal deconvolution of WES and WGS data

To detect subclones in bulk WES and WGS data, we used MOBSTER⁴³, which fits the VAF spectrum with a mixture model containing a Pareto distribution to account for the neutral tail⁹⁷ and a variable number of β-distributions to account for the clonal and subclonal peaks.

We ran MOBSTER using the default parameters, except using a minimum 5% VAF threshold and lowering the minimum number of mutations to compose a cluster to five in WES samples due to the low number of mutations. We then manually quality controlled all 377 WES samples and 10 WGS, tuning the fitting parameters to better represent the data (for instance, when the clonal peak had been called at a low frequency despite the median tumour purity being 95%).

Phylogenetic inference of longitudinal methylation data

A novel Bayesian phylogenetic method was used to reconstruct the evolutionary relationships and the time to MRCA of longitudinal samples from the same patients. This was carried out in the BEAST (v1.8.4) framework^98,99 using custom models implemented in PISCA¹⁰⁰ (v1.1; available from https://github.com/adamallo/PISCA).

EVOFLUx provided an estimate of the age of the patient when the MRCA of each bulk sample emerged. To estimate the methylation status of each fCpG at the MRCA of the sample in each of our longitudinal samples, we discretized the fCpGs as described above (see the section ‘CLL RNA sequencing data’).

We implemented a four-parameter biallelic binary substitution model analogous to the pre-growth EVOFLUx model in PISCA. This plugin contains all the required statistical machinery to use this model for somatic phylogenetic estimation. The biallelic binary substitution model has three relative rate parameters: (1) heterozygous methylation \(\tilde{\upsilon }\), (2) homozygous demethylation \(\tilde{\gamma }\), and (3) heterozygous demethylation \(\tilde{\zeta }\), where homozygous methylation \(\tilde{\mu }\) was normalized to 1. For all relative transition rate parameters, a log-normal prior with mean of 1 and standard deviation of 0.6 was used, with a half-normal prior with mean of 0 and standard deviation of 0.13 for the molecular clock rate, using a strict clock model for the rate of evolution across the tree. Two demographic tree models, constant population size¹⁰¹ and exponential growth¹⁰², were compared by marginal likelihood estimation using path-sampling¹⁰³ and a constant population model was deemed more appropriate.

MCMC chains were run for 100 million generations sampled every 100,000 generations and convergence was assessed using Tracer (v.1.7)¹⁰⁴, ensuring effective sample sizes (ESS) greater than 500 for all parameters. Maximum clade credibility trees were then made using 10% burn-in and medium node heights. The resulting trees were plotted using ggtree¹⁰⁵.

Phylogenetic inference of SNVs from WGS data

Each bulk sample is represented by a set of clonal mutations found during the deconvolution of WGS data (see above). Where a mutation was deemed absent in the clonal peak, the reference nucleotide was used. Mutational signature assignment¹⁰⁶ was used to select mutations in the clock-like SBS1 channel¹⁰⁷. BEAST (v1.10)¹⁰⁸ was then used with the simple binary substitution model (as SBS1 effectively represents just C-to-T substitutions), a strict clock model, a constant population size prior¹⁰¹ and a flat prior on the age of MRCA (from zero to earliest patient sample), with ancestral state estimation at the root. Chains were run and ESS values assessed as described above. The distances between the ancestral state of the root at each MCMC state and the clock rate were used to calculate the expected evolution distance between the root and the known germline. This was used to inform the length of the branch between germline (at birth) and the MRCA of the samples.

Survival analysis

Clinical analyses were performed in CLL for TTFT and overall survival from the time of sampling. Tumour growth rate (θ), effective population size (N_e) and epigenetic switching rates were analysed as continuous variables in univariate Cox regression models for both TTFT and overall survival. The effect size of HRs for each evolutionary variable were analysed considering different scaling factors. In particular, the growth rate was analysed assuming exponential growth (that is, for θ = 1, the population is e = 2.71 times bigger per year), the N_e was considered per million cells, and the cancer age or time from the MRCA was analysed for each 10 years. Individual switching rate parameters (μ, ν, γ and ζ) were largely uninformative of prognosis and were summarized into a mean epigenetic switching rate, which was scaled by a factor of 100. In addition, growth rate and effective population were analysed as continuous variables in multivariate Cox regression models together with TP53 aberrations (considering mutations and deletions together), IGHV gene mutational status and the age of patients at sampling. Kaplan–Meier curves were generated for low and high growth rates and effective population size within IGHV subtypes using maximally selected log-rank statistic using the maxstats package (v0.7-25). P values from Kaplan–Meier curves were derived using the log-rank statistic. Survival (v3.5-7), survminer (v0.4.9) and ggsurvfit (v0.3.1) packages were used under R (v4.3.1). Plots were generated using ggplot2 (v3.5.2).

Estimating the rate of change in lymphocyte counts

Historical records of the absolute number of lymphocytes in blood obtained via haemocytometer were collected for patients with CLL over the whole disease course (that is, an approximate of the number of malignant CLL cells in blood). In 231 patients with CLL, we could obtain at least 10 sample timepoints (that is, at least 10 medical appointments, median n = 27 and mean n = 34) before the first treatment, allowing us to track the natural history of the disease before treatment intervention for the tumour (Supplementary Fig. 10). We fitted a linear model to all 231 cases and obtained the slope of the observed log number of lymphocytes (that is, the coefficient of the univariate linear model) and compared it with growth rate estimates derived from EVOFLUx.

Statistical analysis

Statistical tests performed throughout the study were performed as two-sided. Appropriate multiple test correction, such as the Holm–Sidak correction, is noted when applied.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.