Flexible perceptual encoding by discrete gamma events

Animals

Male and female C57BL/6 mice were kept on a 12-h light–dark cycle, provided with food and water ad libitum, and housed individually following headpost implants. A subset of mice used for optogenetic experiments were heterozygous for PV-ires-Cre (PV–Cre⁺; strain 008069, Jackson Laboratory) or for SST-ires-Cre (SST–Cre⁺; strain 013044, Jackson Laboratory). Mouse cohorts are detailed in Supplementary Table 2. All animals were between 3 and 6 months of age at the time of the experiment. All animal handling and experiments were performed according to the ethical guidelines of the Institutional Animal Care and Use Committee of the Yale University School of Medicine.

Surgery

Mice were anaesthetized with isoflurane (1.5% in oxygen) and maintained at 37 °C for the duration of the surgery. Analgesia was provided with subcutaneous injections of carpofen (5 mg kg⁻¹) or buprenorphine (0.05 mg kg⁻¹). Lidocaine (1% in 0.9% NaCl) was injected under the scalp to provide topical analgesia. Eyes were protected from desiccation with ointment (Puralube, Dechra). The scalp was resected, and the skull was cleaned with betadine. A surgical screw was implanted on the skull between the eyes and nuts were glued to the skull above the bregma suture, allowing the fixation of a headplate with bolts.

For chronic electrophysiology, two craniotomies were performed above V1 on the left hemisphere (approximately 0.15 mm in diameter; 3.75 mm posterior and 2.5 mm lateral from Bregma) and above the cerebellum (0.4 mm diameter; approximately 6 mm posterior from Bregma), respectively. An A16 probe with a CM16 connector (Neuronexus) was lowered into V1. Ground and reference wires were inserted above the cerebellum.

For acute electrophysiology, a circular plastic ring (approximately 2.5 mm in diameter) was glued on the skull above V1. The skull inside the ring was protected with cyanoacrylate.

For optogenetic inactivation of V1 coupled to behaviour, ChR2 was expressed in PV-expressing interneurons as previously described^65,66,67,68. Craniotomies were performed in PV–Cre⁺ mice above V1 (3.75 mm posterior and 2.5 mm lateral from Bregma) on each hemisphere and 1 µl of AAV5-Ef1a-DIO-ChR2-eYFP (Addgene) was injected 300 µm deep at a concentration of approximately 10¹² vg ml⁻¹. Optical canulae (Doric Lenses) were positioned above the dura.

For optogenetic activation of dLGN terminals, ChR2 was expressed in dLGN neurons. 150 nl of AAV1-hSyn-hChR2(H134R)-EYP (Addgene) was injected at approximately 10¹² vg ml⁻¹ on the left hemisphere 2.3 mm posterior and 2.2 mm lateral from Bregma at a depth of 2.7 mm. Mice were then prepared for acute electrophysiology as described above. Alternatively, an optical canula was positioned above the V1 to stimulate dLGN terminals during behaviour.

For optogenetic modulation of dLGN, ChR2 AAV5-Ef1a-DIO-ChR2-eYFP was injected at approximately 10¹² vg ml⁻¹ in the left TRN of SST–Cre⁺ mice 1.3 posterior and 2.05 mm lateral from Bregma as previously described⁵⁰. Two 400-nl injections were performed at 3-mm and 2.65-mm depth. An optical canula was then lowered above the dLGN (2.3 mm posterior and 2.2 mm lateral from Bregma at 2.6 mm deep) and the mouse was prepared for acute electrophysiology as described above.

Craniotomies were protected with Gelfoam (Pfizer), and all implants were affixed to the skull with dental cement.

Electrophysiology

Mice were habituated to handling and head fixation for 3–5 days before electrophysiological recordings. For chronic recordings, mice were head fixed on a wheel and their implants were connected to the recording apparatus (DigitalLynx System, Neuralynx). The most superficial contact point was used as a reference.

For acute silicon probe and patch-clamp recordings, a small craniotomy (0.1–0.5 mm in diameter) was performed above V1 under isoflurane anaesthesia. Analgesic was provided as described above and mice were moved back for more than 2 h in their home cage to recover from anaesthesia. Mice were head fixed on the wheel. The ring situated above V1 was filled with saline, an AgCl reference electrode placed in the bath and an A16 probe (Neuronexus) was lowered into V1.

For optogenetic activation of dLGN terminals, an optic fibre, connected to a 470-nm blue photodiode (Thorlabs) was lowered above the dura on the side of the A16 probe. For dLGN inactivation, the fibre was connected directly to a canula implanted above the dLGN allowing the local optogenetic activation of the terminals of TRN neurons expressing SST. Light power was calibrated before each recording.

For patch-clamp recording, a second craniotomy (approximately 0.1 mm in diameter) was made for patch pipettes of less than 0.1 mm from that used for the A16 probe. The ring above the V1 was filled with artificial cerebrospinal fluid (135 mM NaCl, 5 mM KCl, 5 mM HEPES, 1 mM MgCl₂ and 1.8 mM CaCl₂ (adjusted to pH 7.3 with NaOH)). Glass pipettes (4–6 MΩ) were pulled from borosilicate capillaries (outer diameter of 1.5 mm; inner diameter of 0.86; Sutter Instrument) and filled with an internal solution (135 mM potassium gluconate, 4 mM KCl, 10 mM HEPES, 10 mM phosphocreatine, 4 mM MgATP and 0.3 mM Na₃GTP (adjusted to pH 7.3 with KOH; osmolarity adjusted to 300 mOsmol)). Pipettes were lowered into the V1 and whole-cell or cell-attached patch-clamp configurations were obtained at a depth ranging from 164 to 742 µm. After achieving intracellular access, a minimum delay of 5 min was included before recording to allow cortical activity to recover normal dynamics. Intracellular recordings were amplified with a Multiclamp 700 B amplifier (Molecular Devices).

In all experiments, pupil¹¹ and facial motion⁶⁹ were recorded at 10 Hz using an infrared camera (FLIR). LFPs, wheel motion and timing signals for face movies, visual stimulus and behaviour were acquired at a 40-KHz sampling rate.

Visual stimulation and behavioural hardware

Visual stimuli were generated using the Psychtoolbox MATLAB extension⁷⁰ and displayed on a 17″ × 9.5″ monitor situated 20 cm in front of the animal (visual detection task) or 15 cm from the right eye (all other behavioural tasks; passive visual stimulation). The screen display was linearized, and maximum luminance was adjusted to approximately 140 cd.sr m⁻². An iso-luminant grey background was displayed between visual stimuli. Task-related actions were implemented through sensors and actuators interfaced with a microcontroller (Arduino Due; Teensy 3.2) connected to a computer running custom routines in MATLAB. Waterspouts were positioned using a servomotor (Hi-tec). Responses were detected through an optical sensor (Optex-FA), and water delivery was controlled using solenoid valves (Asco). When behaviour was performed during electrophysiological recordings, timing signals for spout movement, response and reward delivery were sent from the microcontroller to analogue ports on the DigitalLynx System (Cheetah Software versions 5.6.0, 5.7.4 and 6.4.2).

Optogenetic stimulation protocol

Optogenetic stimulation was delivered in 2-s trains separated by 3-s inter-stimulus intervals. For dLGN terminal activation, light output was calibrated at approximately 1–5 mW mm⁻² and 1-ms pulse trains were either regular (20 Hz), Poisson (λ = 24.3 Hz) or drawn from the inter-event interval distribution of gamma events detected by CBASS (Extended Data Fig. 2i; mean of 24.3 Hz). For dLGN inactivation, light was delivered at approximately 50 mW mm⁻² continuously.

Visual stimulation protocol

The visual response of single units was tested using vertical gratings drifting leftwards with a 1-Hz temporal frequency and centred on the receptive field at the recording site. Gratings were presented for 3 s and separated by a 2-s inter-stimulus interval. Unit response properties were investigated at all combinations of 4, 8, 32 and 100% contrasts, 0.01, 0.04, 0.16 and 0.64 cycle per degree spatial frequencies, and 10°, 20°, 40° and 80° diameters (64 combinations total).

Behavioural experiments

For behavioural training, mice were water rationed and maintained between 85% and 88% of their initial weight. Reward consisted of 3 µl water droplets. All visual stimuli were full-screen drifting gratings with a spatial frequency of 0.04 cycle per degree and temporal frequency of 2 Hz and were displayed for 1 s. Auditory stimuli consisted of 2-kHz pure tones. On trials in which mice responded by licking, the stimulus was displayed for an additional 2 s during reward consumption.

Visual detection task

Training was divided into five stages. (1) Mice were first trained to collect water freely from the waterspout. Reward was given at regular intervals. Mice were moved to the next stage when they made 100 responses in a 20-min session. (2) Mice were habituated to the trial structure and to associate reward to high-contrast (100%) visual stimuli. The waterspout was moved within reach, and after a 4-s delay, a pure tone (4 kHz at 200 ms) signalled the onset of a trial. Visual stimuli were displayed after a randomized interval (0.5–1.2 s) and a reward was delivered at stimulus onset. Mice could collect an additional reward if they licked during the visual stimulus. The spout was moved out of reach at the end of trial for an additional interval (1.5–3.5 s). Mice were moved to the next stage after two 30-min sessions. (3) Mice had to lick during visual stimulus presentation (100% contrast) to receive a reward. Mice were moved to the next stage when they responded correctly on more than 80% of trials within a 30-min session. (4) No-go trials were introduced. Stimuli were omitted after the tone on 30% of trials. If animals made a response when stimuli were not present on the screen, the waterspout was moved away, and mice incurred a 10-s timeout. Mice were moved to the next stage when their hit rate was more than 80% and their false alarm rate was less than 20%. Sessions lasted 45 min. (5) Contrast was varied to test psychophysical performance. Task structure was otherwise identical to stage 4.

Visual detection and optogenetics

Mice were trained on the visual detection task until stage 5. After 2–5 days on stage 5, optogenetic stimulation was delivered on 30% of trials through an insulated multimode optical fibre (200 µm in diameter, 0.53 NS, Thorlabs) coupled to a 473-nm solid-state laser (Opto Engine) or through a 470-nm photodiode (Thorlabs). Pulse timing was controlled through transistor-transistor logic (TTL) pulses or a shutter (Thorlabs). Stimulation started 300 ms before stimulus onset and was maintained until the end of the trial. To test the role of V1 in task performance on PV–Cre^+/0 mice, laser power was adjusted to produce an output of approximately 100 mW mm⁻² and 55-ms pulses were delivered at 10 Hz. To test the role of dLGN activation, 1-ms pulses were delivered at an intensity of 3 mW mm⁻² or 5 mW mm⁻² that were either regular (20 Hz), Poisson (λ = 24.3 Hz) or drawn from the inter-event interval distribution of gamma events detected by CBASS (Extended Data Fig. 2i; mean of 24.3 Hz). To test the role of dLGN inactivation on SST–Cre^+/0 mice, light was delivered continuously at an intensity of 50 mW mm⁻².

To investigate how the gamma event rate at response time depended on reward contingencies, we used training schedules consisting of combinations of the following paradigms: spontaneous, task 1 visual, task 2 auditory and forced reward.

Spontaneous paradigm

No stimuli were displayed. Mice were given rewards at Poisson-distributed time intervals (λ = 10 s) to ensure a flat hazard rate. Lick responses made at any time led to additional rewards with an 80% probability.

Task 1 visual paradigm

Rewards were given only when lick responses were made during visual stimuli. Stimuli appeared on the screen at Poisson-distributed time intervals (λ = 9 s).

Task 2 auditory paradigm

Rewards were given only when lick responses were made during auditory stimuli (2-kHz pure tone). The task structure was otherwise identical to task 1.

Forced reward paradigm

Rewards were passively given at the onset of visual stimuli. An additional reward was given upon reward collection. The task structure was otherwise identical to task 1.

Training schedules were always initiated with the spontaneous paradigm in mice having no previous experience in behavioural experiments other than habituation to head fixation and handling.

Preprocessing

Data were analysed in MATLAB 2018b (Mathworks) using custom scripts. All time series were downsampled to 2 KHz (patch-clamp recording) or 1 KHz (chronic recordings) and aligned. LFP recordings were high-pass filtered at 1 Hz using a second-order Bessel filter and z-scored across channels. LFP channels were mapped onto cortical layers using the CSD profile of visual responses (Extended Data Fig. 1l). Recordings of membrane potential (V_m) were curated using a custom-made procedure to delineate epochs suitable for processing. Epochs were retained if (1) the spike threshold was within −40 ± 2 mV, (2) the spike peak was above −20 mV, and (3) V_m values outside spikes stayed in the −85 to −40-mV range. Junction potentials were not corrected but were estimated as −14.9 mV as previously described⁴¹. For event-triggered averages of V_m, spikes were removed from −2 to 5 ms from peak and missing values were interpolated with cubic splines. Pupil diameter was measured from movies with a custom procedure¹¹. Pupil diameter was normalized to the average pupil diameter during locomotion for comparison between recordings. The first principal component of whisker pad motion energy was computed from the same movie using FaceMap⁶⁹. Pupil diameter and facial motion were linearly interpolated and aligned to the other time series. Epochs of running and whisking activity were defined using a change point algorithm detecting local changes in the mean and variance of running speed and whisker pad motion¹¹. Briefly, moving standard deviations of speed and facial motion energy were computed with a defined temporal window. The length t of this window determined the temporal resolution of the change-point analysis and was set to 4 s for running speed and 500 ms for facial motion. A first estimate of locomotion or whisker motion onset or offset times were then taken as the time when the moving standard deviations exceeded or fell below 20% of its range above minimum. Estimates were refined in a window t around each onset or offset time by computing the time points corresponding to the maximum of the t-windowed moving forwards or backwards z score.

Single-unit clustering

Single units were extracted from LFP recording using spikedetekt and clustered using klustakwik2 (Python v2.7.16 and NumPy v1.11.3)⁷¹. Clusters were visualized and sorted using the phy-gui (https://github.com/cortex-lab/phy; Python v3.11.9 and NumPy v1.26.4) together with a custom MATLAB GUI to compute quality metrics. Single-unit clusters were generally retained if less than 0.2% of inter-spike intervals were inferior to 2 ms and if their isolation distance and L-ratio were superior to 15 and inferior to 0.01, respectively⁷². Isolation distance and L-ratio are biased by spike number so deviations to those rules were occasionally allowed for units of low firing rate (less than 200 spikes) if their waveform was well above noise.

Fast-spiking and regular-spiking units were defined as previously described¹¹. In brief, the average normalized waveforms of all units were clustered with the k-means method based on two parameters: peak-to-trough time, and repolarization (that is, defined as the value of the normalized waveform 0.45 ms after peak). Fast-spiking units had higher repolarization values and shorter peak-to-trough times than regular-spiking units.

CBASS

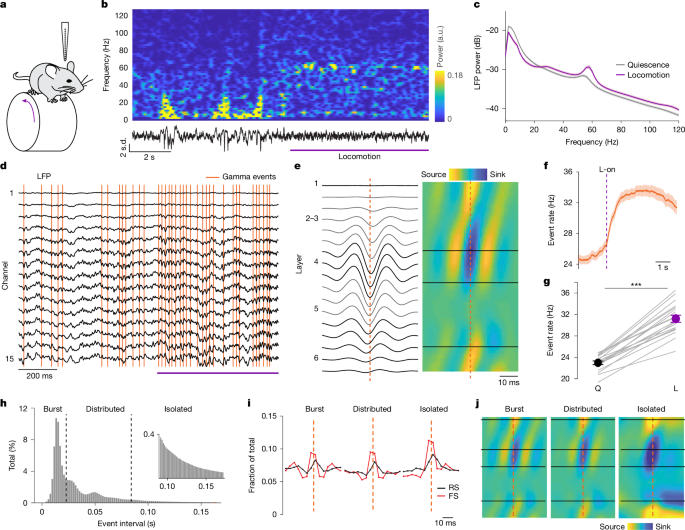
CBASS ties a power increase in a defined frequency band (that is, gamma (30–80 Hz)) during a particular state (that is, locomotion) to the occurrence of defined events in the temporal domain. A detailed description is available in the Supplementary Information and implementations in MATLAB and Python are available on GitHub (https://github.com/cardin-higley-lab/CBASS). In brief, the multichannel LFP is filtered in the band of interest and candidate events are selected at the troughs of the filtered signal in a reference channel (Extended Data Fig. 1a,b). The spectrotemporal dynamics underlying each candidate event were parameterized using the real and imaginary part of the analytical representation (MATLAB function hilbert) of the filtered signal in each channel (Extended Data Fig. 1c). Candidate events form a cloud in this parametric space where neighbours have similar spectrotemporal dynamics (Extended Data Fig. 1d). The event cloud was split randomly into n partitions and a binomial test was performed in each partition to determine whether events happened during the state of interest (that is, locomotion) at higher frequencies than overall. Partitioning was repeated N times (Extended Data Fig. 1e). A state enrichment score was calculated for events as the fraction of time they fell into an enriched partition (Extended Data Fig. 1f). An optimization procedure was then applied to find the threshold yielding the most significant distance between events having a low and a high enrichment score in the feature space (Extended Data Fig. 1g). Events above threshold are retained (Extended Data Fig. 1h). Here we used n = 20 partitions and N = 1,000. Different settings for these parameters have only a marginal influence on the result of the procedure.

To check the validity of the event partition, a state enrichment score was computed as described above on surrogate data having a spectrum and channel covariance matched with that of each recording (Extended Data Fig. 1i). These surrogate data were constructed by decomposing the original LFP recording into principal components across channels (MATLAB function pca), randomizing the phase of their Fourier transform and remixing them. The fraction of candidate events above threshold on surrogate data indicates how likely the pattern may be associated to the state of interest (that is, locomotion) given the statistics of the signal (Extended Data Fig. 1j,k).

Layer alignment of LFP and CSD across recordings

To compute the average field potential around CBASS events across recordings, the LFP was linearly interpolated across channels to a common grid of laminar position. The CSD was derived as the second spatial derivative of the LFP across interpolated laminar positions.

Comparison of naturally occurring and evoked gamma events

The similarity between naturally occurring gamma events and responses to 1–5 mW 1-ms optogenetic stimulation of dLGN terminals was quantified for each session by computing the average CSD, respectively, in a −10 to 10-ms and −5 to 15-ms interval around each. Gamma events were excluded if they fell during a train of optogenetic stimuli to avoid overlap. The cosine similarity between the two average CSD was computed as:

Where \(A_n\) and \(B_n\) are the nth elements of the vectorized CSDs. Significance was estimated by repeating this calculation after randomizing the timing of gamma events in each session and testing for differences between the real and randomized cosine similarities across sessions.

Activity within and outside CBASS event cycles

CBASS events are aligned to the trough of the bandpass-filtered LFP in a reference channel. We defined the boundaries of each event as the peaks surrounding the trough of the event. Peak and troughs were determined as the 0 and π valued time points of the argument (MATLAB function abs) of the analytic representation (MATLAB function hilbert). Activity inside the event boundaries thus fell within a cycle centred on the trough. Epochs during and outside all CBASS event cycles were pooled separately and compared.

Correlation

Correlation between average CBASS events rate, pupil diameter, membrane potential or extracellularly recorded unit firing rate was calculated across 200-ms chunks of the data.

Spike distribution around CBASS events

Spike distribution around CBASS events was computed as follows. For a selected unit, the lag separating each spike from the nearest CBASS events was estimated. A histogram of lag values was then computed and normalized by total spike count. Histograms were averaged across units.

Event rate normalization

Normalized rates for CBASS-detected events were calculated as follows. A baseline event rate p was computed over samples. The variance of the rate over a window of n samples was estimated assuming a binomial distribution as \(s_n^2=np(1-p)\). The normalized rate of events over a window of n samples was then taken as \(r_n=(r-p)/\sqrts_n^2\) where r is the event rate over samples and can be thought of as the number of standard deviations away from baseline.

Unit firing modulation by visual stimulation

Modulation of single-unit action potential firing by visual stimulation was calculated similarly to the normalized event rate. A baseline firing rate r was computed over samples outside visual stimuli. The variance of the rate over a window of n samples was estimated assuming a binomial distribution as \(s_n^2=nr(1-r)\). The modulation of event firing for each stimulus modality samples was then taken as \(r_s=(r_\rmvis-r)/\sqrts_s^2\) where r_vis is the visually evoked firing rate and s is the number of samples within the visual stimulation period. Firing modulation can be thought of as the number of standard deviations away from the mean baseline rate. The baseline firing rate of each unit was computed separately within and outside CBASS event cycles.

Spectral analysis

The spectral power of a given time series was derived with Welch’s method. Each channel was divided into 500-ms overlapping segments (75% overlap). Each segment was multiplied by a Hamming window and their Fourier transform was computed (MATLAB function fft). Power was derived as 10 times log₁₀ of the squared magnitude of the Fourier transform and expressed in dB. Power was averaged over segment and channels.

The spectral power of event-triggered averages was derived with a minimum bias multitaper estimate⁷³. This differs from a classical multitaper estimate in that Slepian tapers were replaced by a sinusoidal taper sequence defined as:

where N is the number of samples in the triggered average, n is the sample number and k is the order of the taper. Sinusoidal tapers produce a spectral concentration almost comparable with that achieved with a Slepian sequence while markedly reducing local bias. The number of tapers was chosen to yield a bandwidth of 0.8 Hz following the formula: \(K=\rmround((4\pi NB/r)-1)\) where B is the bandwidth and r is the sample rate. Triggered averages were multiplied by each taper. Spectral power was then computed as described above and averaged over tapers.

For coherence and spike-phase locking estimation, spectrotemporal representations were first derived either for a set of frequencies using a wavelet transform (MATLAB function cwt) and a Morlet wavelet (MATLAB identifier cmor1-2) or across a full frequency band by computing the analytical representation of the filtered signal (MATLAB function Hilbert). Coherence was defined as:

where S_k(n) is the spectrotemporal representation of signal k for sample n at the frequency f. κ_f has a positive bias of (1 – κ_f)/N where N is the number of samples^74,75. The bias was subtracted from the estimate. Spike-phase locking was estimated using the PPC⁷⁶ defined as:

where θ_k is the phase of the signal for frequency f at the time of spike k and N is the total number of spikes. PPC provides an unbiased estimate of spike-phase locking. However, estimates can be noisy if the spike number is inferior to 250. Thus, population estimates of PPC were derived by pooling spikes from all selected neurons and the variance over neurons was estimated with a leave-one-out Jackknife procedure⁷⁷.

Logistic regression

Logistic regressions of trial outcome in our visual detection task were performed using the MATLAB function glmfit and a logit transfer function. Logistic regression models return an estimation of the probability of response for each trial. The log-likelihood of regression models was calculated by summing the log-likelihood of the outcome of each trial given the probabilities returned by the model and assuming a Bernoulli distribution. Model performances were tested using likelihood ratio tests and quantified with McFadden’s R² and a sensitivity metric (d′). McFadden’s R² was defined as:

where LL_model represents the log-likelihood of the regression and LL₀ represent the log-likelihood of the null model (that is, the likelihood of the data assuming that all trials have an equal probability of success corresponding to the mean hit rate). Sensitivity was defined as

where Z is the inverse standard normal distribution, and P_resp and P_rej represent the average probability of response returned by the model for response and rejection trials, respectively. The impact of each regressors was assessed in two ways. (1) Regression was recomputed 1,000 times after shuffling the values of the regressor over trials. A P value for the significance of the impact of each regressor was derived as the percentage of R² on shuffled values superior to the actual R² of the model. (2) Regression models were compared with a model in which each regressor was taken away and the significance of the contribution of the regressor was estimated with a likelihood ratio test. The magnitude of the contribution of a regressor was measured using the increase in deviance. Deviance represents the difference of predictive power from a saturated model giving a perfect prediction (that is, the likelihood of each trial is 1). It was defined as:

where LL_model is the log-likelihood of the model and LL_sat is the log-likelihood of the saturated model. Significance was estimated separately for each mouse. Statistical significance across mice was assessed by pooling P values using the Fisher’s method.

Statistics and reproducibility

A detailed description of the statistical test in each figure panel and of statistical samples is provided in Supplementary Tables 1 and 2, respectively. Except where otherwise noted, tests were performed using mice as the statistical unit. All t-tests were two-sided Student’s t-tests. When indicated, independent P values derived on individual mice were pooled using the Fisher’s method. Multiple comparisons were corrected using the Benjamini–Yukutieli procedure for false discovery rate⁷⁸.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.