JWST observations and data reduction and analysis
Data
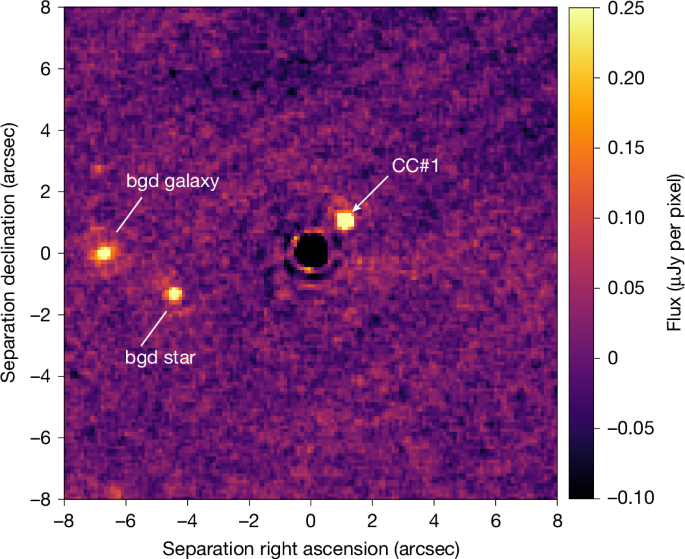
Coronagraphic observations were performed with the 4QPM_1140 coronagraph paired with the F1140C filter. The details of the observations are given in Extended Data Table 1. We obtained two roll angles (difference of 7.835°) to mitigate the attenuation of the coronagraph in the field of view, in case an object falls close to one phase transition of the 4QPM. Each coronagraphic observation was 2 h long, hence a total of 4 h on the science target. Background observations were observed immediately after the science exposures in a two-point dithering mode, for a total of 4 h.
A reference star, CD-23-9765, was observed back-to-back with the target in the same configuration with the aim to subtract the starlight diffraction after the coronagraph. The reference shares similar brightness and spectral type with the target, and is angularly close. It was observed with nine-point small-grid dithering (SGD) to apply post-processing algorithms such as principal component analysis (PCA)36. In total, the reference star was observed for about 1 h and comes with dedicated background observations.
Using comparison with simulated coronagraphic images, as in ref. 37, we were able to estimate a pointing accuracy on the 4QPM of about 2 mas per axis, significantly lower than the 10-mas step of the SGD. We also confirmed the detector coordinates of the 4QPM_1140 mask (119.758, 112.158 as provided in the JWST Calibration Reference Data System).
Data analysis
The data reduction follows the steps described in refs. 21,38. Level 1 data are retrieved from the Mikulski Archive for Space Telescopes (MAST), processed with v1.14.0 of the pipeline together with Calibration Reference Data System file 1241. Images are registered to the coronagraph centre. Calibrated files (‘cal’ files) are produced in-house with the JWST pipeline for each roll, by subtracting the background and converting the photometric units (data numbers per second to mega-janskys per steradian). The background is built from the minimum per pixel of the two dithers. We skipped the flat-field correction, which is not appropriate for the MIRI coronagraph22.
We took advantage of the diversity brought by the SGD mode to build a reference frame to subtract the stellar diffraction. We tested various algorithms and retained a linear combination (which uses the downhill simplex minimization) of the nine SGD reference star images, as well as the PCA, as the two algorithms providing the best detection of CC#1. To mitigate the over-subtraction effect, a numerical masking is implemented to ignore some parts of the image. We obtained the best compromise by selecting the annular region between 0.5 arcsec and 3 arcsec, and the three sources were masked with a 1 λ/D patch, with λ representing the observing wavelength and D the telescope diameter (we checked that the CC#1 flux measurements are similar with a different region: 2–3 arcsec). We proceeded similarly for the PCA, using eight components to build the final image that is subtracted to the data, in an annular region from 0.5 arcsec to 5 arcsec (point sources not masked). Despite the bad-pixel correction applied on the raw coronagraphic images, the subtracted images with the reference star are still affected by a few bad pixels, both with the linear combination and PCA. We further apply a σ-clipping function to correct for these remaining bad pixels. Finally, the images are rotated to align north up, considering the aperture position angles: 121.45° for roll 1 and 129.27° for roll 2, as well as the V3 axis orientation on the detector (4.835°).
Next, extracting the flux and position of the CC#1 requires modelling its point spread function (PSF), which can vary spatially and nonlinearly owing to the attenuation of the coronagraph for which the phase transitions extend across the whole field of view. We used both the diffraction code developed in refs. 39,40 and WebbPSF41 to simulate the MIRI PSF, taking into account the coronagraph, considering the configuration of mask, stop and filter (‘FQPM1140’, ‘MASKFQPM’ and ‘F1140C’, according to the WebbPSF terminology). The position of CC#1 is approximated with a Gaussian fit, passing the sky coordinates to the former diffraction code and detector coordinates to WebbPSF to calculate the PSF of CC#1 accounting for the coronagraph attenuation. We measured the coronagraph transmission with both PSF estimates. The flux of the PSF model at the position of CC#1 is integrated in a 1.5 λ/D aperture (to match the aperture used for photometric measurements), and compared to that at 10 arcsec (far away from the coronagraph influence). The two approaches give similar transmissions: 0.66 and 0.62 in roll 1 and 0.31 and 0.28 in roll 2. Therefore, CC#1 is significantly closer to one 4QPM transition in roll 2 than in roll 1, so both its astrometry and photometry can be affected (Extended Data Fig. 1). We measured a signal-to-noise ratio of 30 and 18, respectively, for roll 1 and roll 2, using the linear combination method. In the roll 2 image, the PSF is more asymmetrical as the planet is closer to the quadrant edge in comparison to roll 1, so we decided to consider only roll 1 data for the photometric analysis.
On the basis of these CC#1 PSF models, we extracted the flux and the photometry of the object by minimizing the residuals between the reduced JWST data and a PSF model in a 1.5 λ/D area with three free parameters (positions and flux) and using either a downhill simplex algorithm or the Nelder–Mead algorithm42. For comparison, we also used aperture photometry, but this required implementation of an aperture correction based on simulated PSF (ratio of the total flux in the PSF to the flux integrated in the 1.5 λ/D aperture).
The flux extraction is applied both on the photometrically calibrated files (.cal), which directly provides CC#1 flux in mega-janskys per steradian, and on the uncalibrated files (.rate), which requires to measure a contrast with respect to the non-coronagraphic image of the star. As detailed previously22, the contrast measurement relies on commissioning data either on target acquisition images that come with the telescope pointing procedure but are obtained with a neutral density filter, or from images obtained on and off the coronagraph on another star. The method using target acquisition shows some net discrepancies, probably because the target acquisition filter is very broad (about 8–18 μm) and the targets have different spectral types (M3 for TWA 7 and K0 or K5 for the commissioning targets). Besides, the emission of the TWA 7 disk is expected to become significant beyond 15 μm. As a result, we did not use the target acquisition method in the following. The final photometric values are based on the linear combination and PCA technique to suppress the starlight. We averaged the values of the different methods (calibrated files and contrast, aperture and PSF model for the photometric extraction) and the error bar is built from the extreme values ((max − min)/2) for being conservative. We measured a flux density of 5.60 ± 0.97 × 10−19 W m−2 μm−1 for CC#1. The fluxes of the other sources are given in Extended Data Table 2. Note that we also tested the typical ‘injection–recovery’ method directly in the raw data, but did not notice any significant differences for the extracted flux of the planet.
Estimation of the probability for an intermediate-redshift star-forming galaxy
To estimate the probability that the source labelled CC#1 is a galaxy, we have taken into account the three constraints on the fluxes or upper limits at 1.6, 11 and 870 μm. The source has a flux of 22 μJy at 11 μm, and is not detected with ALMA at 870 μm, but with a tapered resolution of 2 arcsec. The measured 3σ upper limit for an unresolved source at the position of the MIRI source is 96 μJy (ref. 21). Combining all ALMA observations (see Extended Data Fig. 5), the 3σ upper limit is 76 μJy, in a beam of 0.29 arcsec × 0.24 arcsec (see a detailed analysis and estimation in the Supplementary Information). The third constraint is from the non-detection at 1.6 μm with VLT SPHERE, with an upper limit of approximately 0.6 μJy for a point source (about 60 mas in size). However, we have to take into account the fact that a low-z galaxy could be extended in the calculation of its maximum flux at 2 μm. Indeed, the size of a galaxy is expected to vary from one wavelength to the other: at 1.6 μm, the disk of old stars dominates, so the source is more extended, of the order of 10 kpc, whereas at 11 μm and 870 μm, the nuclear star-forming region dominates, and will appear more concentrated, of the order of 100–500 pc. We therefore considered the flux limit of an extended (0.6 arcsec) source in the SPHERE data (that is, 60 μJy).
Two types of galaxy might comply with these three constraints: star-forming galaxies or active nucleus (AGN) or a combination of both, with a redshift between z = 0.1 and 1. For such galaxies, at lower redshifts, where 1 arcsec is smaller than 2 kpc, the source would probably look extended (up to 5 arcsec) for wavelengths between 1 and 4 μm (ref. 43). At higher redshifts, the peak of the emission usually located at 100 μm will enter the ALMA domain at about 1 mm, and it should have been detected by ALMA44.
As the density of the cosmic star formation rate increases considerably with redshift between z = 0 and 1, starbursts at z = 0 are good templates for star-forming galaxies at z = 0.1 to 1. The starburst is in general nuclear. It can be highly peaked in the centre, or distributed in a ring of about 100-pc radius (like in M82), but the emitting size at 100-μm rest frame will be no more than typically 1 kpc. This corresponds to an angular size of about 0.55 arcsec at z = 0.1, about 0.16 arcsec at z = 0.5, and about 0.12 arcsec at z = 1. We also considered AGN templates. The nucleus is then a point source at long wavelengths, while the galaxy host is extended (about 10 kpc) at the shortest wavelengths.
The probability to find a z = 0.1 to 1 star-forming galaxy with a flux at 11 μm of 22 ± 3.8 μJy (hence, within a range of 7.6 μJy) in a field of view of 10 × 10 arcsec can be estimated readily through the source counts, from refs. 45,46,47,48. A probability of 50% is found in the redshift range z = 0.1 to 1.
To take into account the other constraints at 1.6 and 870 µm, we used the Spitzer Wide-Area Infrared Extragalactic Survey (SWIRE) templates, from ref. 49, http://www.iasf-milano.inaf.it/~polletta/templates/swire_templates.html which include 14 templates of starbursts and AGN, representative of star-forming and active intermediate-redshift galaxies. These templates were computed for a half-dozen redshifts, and calibrated to have a flux of 22 μJy at 11 μm. An illustrative plot of their spectral energy distribution (SED) is shown in Extended Data Fig. 2, in which the flux constraints at 1.6 and 870 µm are also indicated by black symbols (square and triangle).
We used the rest-frame 8-μm luminosity function of galaxies at redshifts between z = 0.1 and z = 1 in the Great Observatories Origins Deep Survey (GOODS) fields50 to estimate the abundance of these star-forming galaxies. The 8-μm luminosity was deduced from the templates. This led to a probability of 12% to find such a galaxy in the right redshift range (z = 0.1 to 1) in the 10 × 10 arcsec field of view. We estimated that there are about 80% star-forming galaxies and 20% active nuclei, including low-luminosity ones such as Seyfert galaxies51,52. As can be seen in Extended Data Fig. 2, all templates comply with the three constraints below z = 0.5, and some starbursts are found brighter at 870 μm above this redshift. We therefore reduced the probability accordingly for z > 0.5, attributing each star-forming template equal probability, as shown by the observations53. The final probability to find such a galaxy in the 10 × 10 arcsec field of view is about 5%, with significant uncertainties: +3/−2%. Hence, in a radius of 1.5 arcsec around TWA 7, the probability to have such a galaxy is about 0.34% (+0.22/−0.14%). We note that the distribution of galaxies on the sky might be clustered in some rare places, and our error bars should be increased, but no more than 30% given the typical errors on luminosity function of galaxies45,47,50. Altogether, the probability of having a galaxy satisfying the various constraints within 1.5 arcsec would be 0.34% (+0.29/−0.18%). Note that the current calculation applies to these specific observational constraints. The probability for CC#1 to be a rare type of background galaxy compatible with the JWST, ALMA and SPHERE observational constraints is therefore low. Such a low-probability event can admittedly arise would a large number of independent datasets be analysed. However, this is not the case for this study. Indeed, only two datasets among about 30 JWST MIRI datasets dedicated to exoplanet searches are analysed. Moreover, most of the other datasets are not as deep as the present ones, and there are no corresponding 1.6- and 870-μm data available. Hence, the likelihood that any research group would have found such a peculiar background galaxy contaminant within the whole corpus of relevant JWST data is much lower than the simple 10.2% (30 × 0.34%) one could derive.