Efficient quantum thermal simulation | Nature

We provide the explicit form of our construction and explain how exact detailed balance can be achieved through the key algorithmic subroutines and circuits.

Constructing the full Lindbladian

Recall that our main result considers the following Lindbladian in the Schrödinger picture:

Roughly, it resembles the Davies generator (equation (5)) but is carefully modified to maintain quantum detailed balance while ensuring locality and efficiency. We begin by reviewing the detailed balance condition for the Davies generator to illustrate the key ingredients and differences in our construction. We may regroup the above according to the jumps \(\mathcalL=\sum _a\in A\mathcalL^a\), and study each term individually, so in what follows we drop the label a for simplicity, that is, substitute A^a ← A.

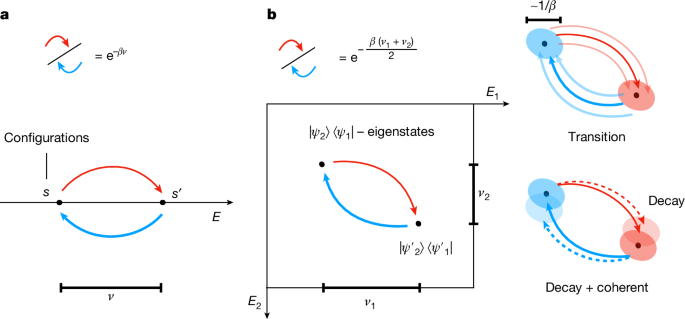
Detailed balance of the Davies generator

For a Hermitian jump A, recall that the Davies generator \(\mathcalL_Davies[\cdot ]\,:= \,\sum _\nu \gamma (\nu )A_\nu [\cdot ]A_\nu ^\dagger -\) \(\frac\gamma (\nu )2\A_\nu ^\dagger A_\nu ,\cdot \\) satisfies the KMS-detailed balance condition (equation (4)), that is, satisfies the superoperator equation

where \(\mathcalL^\dagger \) is the superoperator adjoint of \(\mathcalL\) defined by \(\rmTr[(\mathcalL[X])^\dagger Y]=\rmTr[X^\dagger \mathcalL^\dagger [Y]]\) for all X, Y. Here, detailed balance hinges on the following exact operator-valued symmetries: for all Bohr frequency ν ∈ B(H), 

The conjugation identity is rooted in that A_ν are eigenoperators [H, A_ν] = νA_ν of the commutator [H, ⋅ ], highlighting a special role played by the Bohr-frequency decomposition A_ν. The adjoint property says that for a Hermitian jump A, the transition amplitudes associated with energy difference ν are paired with the reverse difference –ν, reminiscent of a Fourier transform symmetry of real functions.

As a consequence, the decay part readily satisfies detailed balance by itself because of the adjoint property, because the operator \((A_\nu )^\dagger A_\nu =A_-\nu A_\nu \) in the decay part preserves the energies and commutes with the Hamiltonian (and hence with ρ). For the transition part,

The second equality uses the Kubo–Martin–Schwinger condition (in the frequency domain) for the transition weights

The main obstacle towards a Lindbladian with exact detailed balance and efficient implementation is the lack of algorithmic access to A_ν in the presence of a dense spectrum, as approximations to A_ν can easily break the exact symmetry conditions in detailed balance^18,20,51.

Operator Fourier transforms

The key to both efficiency and exact detailed balance is a careful relaxation of A_ν that preserves some aspects of the symmetries using the operator Fourier transform damped by a Gaussian filter \(f(t)\,:= \,\rme^-\sigma ^2t^2\sqrt\sigma \sqrt2/\rm\pi \) (normalized by \(\int _-\infty ^\infty f(t)^2\rmdt=1\)) with a tunable width ∝ 1/σ (setting \(\sigma =\frac1\beta \) recovers (equation (6)):

Like A_ν in the Davies generator (equation (5)), our operator Fourier transforms \(\widehatA(\omega )\) are labelled by energy differences, but here the parameter ω ∈ [−∞, ∞] takes continuous values, without referring to the true Bohr frequencies. When the uncertainty vanishes σ → 0, we recover \(\mathop\mathrmlim\limits_\sigma \to 0\sqrt\sigma \sqrt2\rm\pi \widehatA(\omega )=\sum _\nu \in B(H)\mathbb1(\nu =\omega )A_\nu \); when the energy uncertainty is finite σ ≠ 0, the operator Fourier transforms still maintain exact algebraic properties crucial for detailed balance. First, conjugating with the Gibbs state preserves the form of operator Fourier transforms, albeit causing a shift and rescaling

which reflects the fact that multiplying a Gaussian distribution by an exponential weight must shift the mean \(\rme^(x-a)^2-2bx=\rme^(x-a-b)^2-2ab-b^2\). Second, even though the operator Fourier transform is a linear combination of different Bohr frequencies, the adjoint property holds exactly when A = A^† as

The above two exact symmetries appear to be absent in previous approaches that attempted to directly measure energy differences. Now we show that quantum detailed balance is a consequence of these exact symmetries and related algebraic properties of the Gaussian uncertainty in operator Fourier transforms, which hold exactly despite not measuring energies to high precision.

Exact detailed balance with finite uncertainty

Although the operator Fourier transform does not yield an exact representation of A_ν, the uncertainty has a specific structure with distinctive symmetries—arising from the interplay between the Gaussian weighing and the exponential form of the Boltzmann factors—and consequently can be exactly compensated by an appropriate shift in the transition weights. In the following, we prove that the transition part (equation (9)) satisfies detailed balance (equation (10)): \(\mathcalT\,[\cdot ]=\rho ^\frac12\mathcalT^\dagger [\,\rho ^-\frac12\cdot \rho ^-\frac12]\rho ^\frac12\). The above shift-rescale and adjoint symmetries yield

showing that we may compensate for the uncertainty by imposing a shifted KMS condition (equation (12))

Therefore, we can take any transition weight function satisfying the KMS condition γ₀(ν)e^βν = γ₀(−ν) and pretend we underestimated the Bohr frequency by \(\frac\sigma ^2\beta 2\), that is, substitute \(\nu \leftarrow \omega _+:= \omega +\frac\sigma ^2\beta 2\) to obtain our shifted γ(ω). The canonical examples include the Metropolis and Glauber weights

See ref. ³³ for the original step-by-step detailed derivation; the above streamlined derivation draws partly from subsequent simplification and development (Lemma 7.1 of ref. ⁵² and Lemma IX.2 of ref. ⁴⁹).

Under the natural normalization γ(ω) ∈ [0, 1], the shifted symmetry (equation (15)) implies a low transition rate \(\gamma (0)\le \exp (-\sigma ^2\beta ^2/2)\) around ω = 0. Therefore, to avoid unnecessary idling of the process, it is imperative to choose an uncertainty σ ≤ 1/β not exceeding the temperature; in the main text, we have simply set \(\sigma =\frac1\beta \). This is why implementing a single step uses ~β Hamiltonian simulation time in our construction. By contrast, for classical or commuting systems with gapped periodic spectrum, the uncertainty can be discretized, and there is no need to scale the Hamiltonian simulation time with β.

Achieving full detailed balance by tuning the coherent term

Even if the transition part (equation (9)) satisfies detailed balance exactly, the decay part D of the Lindbladian may still break detailed balance when it does not commute with the Hamiltonian H.

A second insight of our construction is to prescribe and efficiently implement a dedicated coherent term C that perfectly cancels out the deviation from quantum detailed balance in a uniquely quantum way, as shown by the following lemma.

Lemma 1: prescribing the coherent term

(Lemma II.1 of ref. ³³) For any full-rank density operator \(0\,\prec \,\rho \in \mathbbC^d\times d\) and Hermitian operator \(D\in \mathbbC^d\times d\), there is a unique Hermitian operator \(C\in \mathbbC^d\times d\) (up to adding any scalar multiples of the identity I) such that the superoperator

satisfies ρ-detailed balance. For a Gibbs state \(\rho \propto \exp (-\beta H)\), we can express C as

Proof

The detailed balance condition is equivalent to the following matrix being self-adjoint:

This is self-adjoint because \((D_\nu )^\dagger =D_-\nu \), \(\cosh (x)=\cosh (-x)\), and B(H) = −B(H). □

See also ref. ⁵³ on prescribing fixed points in general, without necessarily assuming detailed balance. The coherent term C is a Hermitian matrix obtained by reweighing the given D operator with the profile \(\rmi\,\tanh (\beta \nu /4)/2\) on each Bohr frequency component D_ν. The coherent term is completely determined by ρ and D (ref. ⁵⁴), and we found a particularly simple and useful closed-form representation in the time domain (recall \(\rmsinhc(x)\,:= \,\sinh (x)/x\) for real x ≠ 0)

which in turn implies the algorithmic efficiency and quasi-locality of the coherent term. The above integral form and the exponential decay in t allow using the linear combination of unitaries technique to implement a block encoding of C (refs. ^33,55) by truncating and discretizing the time integral. For the Davies generator (equation (5)), we have that [H, D] = 0. Therefore, the dissipative part readily satisfies detailed balance, and D_ν = 0 for all ν ≠ 0, implying that the above coherent term prescription simply vanishes.

Quasi-locality

A salient feature of our construction is the quasi-locality of the Lindbladian terms, inherited from the operator Fourier transform in systems that feature a Lieb–Robinson bound. For all \(\omega \in \mathbbR\) and geometrically local jump A, truncating the Hamiltonian to a local Hamiltonian patch H_ℓ within distance ℓ from the jump yields an error

For a wide variety of local Hamiltonian systems, off-the-shelf Lieb–Robinson bounds³⁰ for the Heisenberg dynamics e^iHtAe^−iHt state that the integrand in equation (21) exponentially reduces with the distance ℓ but degrades with the evolution time t. As the Gaussian weight function f(t) of equation (13) effectively dampens the integral to small values of t ~ 1/σ, the operator \(\widehatA_(H)(\omega )\) is well-approximated by a Hamiltonian patch with radius scaling with the energy uncertainty σ, which can be independent of the system size. See, for example, Appendix A of ref. ⁴⁹ for a quantitative estimate for both the transition and coherent parts. Of course, after truncation, the resulting strictly local Lindbladian may no longer satisfy exact quantum detailed balance.

Fixed point and its uniqueness

The detailed balance condition (equation (10)) directly implies that the Gibbs state ρ is a fixed point for the Lindbladian \(\mathcalL\).

where the last equality used the trace-preservation property \(\mathcalL^\dagger [I]=0\) of Lindbladians.

We now explain why the Gibbs state is the unique fixed point whenever the set of jump operators has no (nontrivial) invariant subspaces, which holds, for example, when the jumps include all single-site Pauli X and Z operators. Decomposing each jump operator by the operator Fourier transform \(A^a\propto \int _-\infty ^\infty \widehatA^a(\omega )\rmd\omega \) cannot create new invariant subspaces; likewise, multiplying by strictly positive transition weights γ(ω) cannot. Thus, the resulting set of Lindblad operators \(\sqrt\gamma (\omega )\widehatA^a(\omega )\) has no invariant subspaces, which is known⁵⁶ to imply the uniqueness of the fixed point. But this uniqueness argument says little about the quantitative convergence rate, and the mixing times can depend on the particular Hamiltonian.

A single-qubit example

Let us illustrate the details of our Lindbladian construction through a pedagogical example. Consider a single-qubit Hamiltonian with a single jump:

The eigenvalues of the Hamiltonian are ±1, and the Bohr frequencies, their differences, are B(H) = 2, 0, −2. We can decompose the jump by the Bohr frequencies, into the ν = 2 and ν = −2 components as follows:

We can then directly obtain the Davies generator for any transition weights satisfying γ(2)e^2β = γ(−2). By contrast, our operator Fourier transform yields

Thus, for all \(\omega \in \mathbbR\) the resulting \(\widehatA(\omega )\) has contributions coming from both the A₂ and A₋₂ components; these components only get separated in the σ → 0 limit. Nevertheless, detailed balance still holds at every finite uncertainty σ with suitable choices of γ(ω) (equation (15)) and the additional coherent term.

Recovering the Davies generator

As we show here, our Lindbladian exactly recovers the Davies generator in the σ → 0 limit. Moreover, the Davies generator reduces to Glauber dynamics when the Hamiltonian H is a classical function of bitstrings and the jumps A map a bitstring to another: in this case, inputs that are a probabilistic mixture of bitstrings undergo a classical Glauber dynamics (see section ‘Quantum MCMC by master equations for thermalization’).

For any bounded, continuous function γ₀ satisfying the KMS condition γ₀(ν)e^βν = γ₀(−ν), consider the shift \(\gamma _\beta \sigma (\omega )\,:= \,\gamma _\left(\omega +\frac\beta ^2\sigma ^22\right),\) then the transition part (similarly for the decay term) converges to

When we expand the left-hand side as a sum over \(A_\nu _1[\cdot ](A_\nu _2)^\dagger \), the coefficients for each ν₁, ν₂

approach the corresponding value in the Davies generator. By contrast, the coherent term vanishes, because the decay term commutes with the Hamiltonian in the σ → 0 limit and tanh(0) = 0 (see Lemma 1).

Implementation

In this section, we give low-level quantum algorithmic implementations of our Lindbladian dynamics.

A phase estimation for operators

The most general form of the discrete operator Fourier transform is a subroutine similar to quantum phase estimation: it combines controlled Hamiltonian simulation with the quantum Fourier transform, as shown in Fig. 3a, acting on the time–frequency and system registers. To approximately implement the (continuous) operator Fourier transform, we need to discretize the time integral by introducing a time mesh \(\bart\in S_t_\) and a corresponding frequency mesh \(\bar\omega \in S_\omega _\) for the QFT, each having M points, resulting in the discretized operation

As given in Corollary C.2 of ref. ²², choosing

the above equation (25) recovers the advertised continuous operator Fourier transform (equation (13)) in the M → ∞ limit. As f is a smooth Gaussian function, we can achieve any finite precision ϵ-approximation of the dissipative part of \(\mathcalL\) with a moderately scaling dimension \(M \sim \rmPoly(\parallel H\parallel ,\beta ,1/\epsilon ,\sigma +1/\sigma ,| A| )\), which requires only \(\log (M)=\widetilde\mathcalO(1)\)-many ancilla qubits, and no more than \(\mathcalO(\sqrt\log (1/\epsilon )\,/\sigma )\) (controlled) Hamiltonian simulation time, because of the truncation of the Gaussian tail.

A general-purpose Lindbladian simulation algorithm

Another key algorithmic component is an improved black-box Lindbladian simulation subroutine. It achieves the sought nearly linear dependence on t even for Lindbladians with high Kraus rank, as long as the Lindblad operators are given in a block-encoded form, which represents an improvement on previous Lindbladian simulation algorithms^51,57.

Definition 1: block encoding for Lindblad operators

(Definition I.2 of ref. ²²) We say that a unitary U is a block encoding for Lindblad operators L_j: j ∈ J, if

In particular, discretized operator Fourier transforms (equation (25)) naturally give block encodings of this form, where J refers to the discretized set of frequency labels \(S_\omega _\). Given a block encoding U of the Lindblad operators as above, we can directly obtain a block encoding of the decay term D by a single use of U and U^† by standard multiplication of block-encoded matrices¹¹. As a consequence of the exponentially decaying tails in the integral representation of equation (20), by using an additional ~ β-time controlled Hamiltonian simulation and the linear combination of unitaries (LCU) technique⁵⁵, we can also obtain a sufficiently good approximate block encoding of the coherent term C.

We begin with a brief analysis of the first-order simulation circuit shown in Fig. 3b. Assuming the system register is in the pure state |ψ⟩, the first three gates act as follows (for simplicity, we drop the superscripts A^a ← A):

where \(| ^q\perp \rangle \) is a quantum state such that \(\parallel | ^q\perp \rangle \parallel \le 1\) and \((\langle ^q| \otimes I)\cdot | ^q\perp \rangle =0\), see Theorem III.1 of ref. ²², for details.

Let \(| \psi ^\prime \rangle \) be the resulting state in equation (28), and let us denote the dissipative part \(\mathcalL^\prime := \mathcalL^a+\rmi[C^a,\cdot ]\). Tracing out the first q + 1 qubits, we get that \(| \psi ^\prime \rangle \) is \(\mathcalO(\delta ^2)\)-close to the desired state, ignoring the coherent term. We now show that

by observing that

Convexity and the triangle inequality imply that equation (29) also holds for mixed input states. By including the δ-time Hamiltonian simulation for C^a, we get an \(\mathcalO(\delta ^2)\) approximation of δ-time evolution by \(\mathcalL^a\). Once again, owing to linearity and the triangle inequality, this also implies that performing the circuit Fig. 3b for a uniformly random jump A^a we get a δ-time evolution by \(\frac1A\sum _a\in A\mathcalL_a\) up to \(\mathcalO(\delta ^2)\) error in trace distance, see Corollary III.1 of ref. ²². Repeating the entire argument after replacing the jump operators A^a by A^a ⊗ I, we can see that actually the above results in a \(\mathcalO(\delta ^2)\)-precise implementation of the quantum channel \(\exp \left(\frac\delta A\sum _a\in A\mathcalL_a\right)\) in the completely bounded 1-1 superoperator norm, that is, the diamond-norm.

Choosing \(\delta =\varTheta \left(\frac\epsilon t\right)\) ensures that the error in a single time step is bounded by \(\mathcalO\left(\frac\epsilon ^2t^2\right)\), and repeating the process \(\varTheta \left(\fract^2\epsilon \right)\)-times induces an error that is bounded by ϵ for the entire time-t evolution. The complexity is then \(\varTheta \left(\fract^2\epsilon \right)\) times the cost of implementing the circuit in Fig. 3b.

Building on the compression techniques in ref. ⁵⁷, we can bootstrap the first-order weak-measurement circuit of Fig. 3b by observing that for very small time steps, the circuit is very close to identity. Exploiting this by effectively only using the circuit Fig. 3b in parts of the trajectories that are nontrivial, we can achieve almost linear scaling in t and polylogarithmic scaling in the desired diamond-norm accuracy of the simulation. However, we need to apply some modifications, as it turns out the original compressed measurement scheme described in ref. ⁵⁷ does not work as intended. Thus, we use a variant of the analogous measurement scheme described in ref. ⁵⁸ (see Appendix F of ref. ²², for more details). This amounts to our ultimate near-linear-time simulation result.

Theorem 2: almost linear-time Lindbladian simulation

(Theorem III.2 of ref. ²²) Suppose U is a unitary block encoding of the Lindblad operators of \(\mathcalL\) as in Definition 1, and V is a block encoding of the coherent term C. Let t ≥ 1 and ϵ ≤ 1/2, then we can simulate the map \(e^\mathcalLt\) to error ϵ in diamond norm using

where q is the number of ancilla qubits used for the block encodings.

To place the above general result in context, we give some simple bounds on the resources required for implementing our Lindbladian. For instance, if the jump operators are K different Pauli strings, then \(q=\log _2(K)+1\) ancilla qubits suffice for block encoding them. The overall gate complexity should be dominated by the controlled Hamiltonian simulation subroutine. Thus, we focus on estimating the required Hamiltonian simulation time per call to U and V (assuming an operator Fourier transform width \(\sigma =\frac1\beta \)). Under the normalization \(\parallel \sum _a\in AA^a\dagger A^a\parallel \le 1\), the Lindblad operators from our construction (equation (7)) can be ϵ-accurately block-encoded by discretized operator Fourier transform using \(\mathcalO(\beta \sqrt\log (1/\epsilon ))\) (controlled) Hamiltonian simulation time by truncating the Gaussian integrand in equation (6). Meanwhile, as implied by Corollary III.2 of ref. ³³, a slightly subnormalized coherent term C/α for \(\alpha =\mathcalO\left(\log \left(\frac\beta \,\parallel \,H\,\parallel \epsilon \right)\right)\) can be ϵ-accurately block-encoded by LCU by using a mere \(\mathcalO(\beta \,\log (1/\epsilon ))\) (controlled) Hamiltonian simulation time. The extra subnormalization factor α can be absorbed into the number of uses of the block encoding V using state-of-the-art block-encoded Hamiltonian simulation techniques^4,11.

To approximate \(e^\mathcalLt\) to ϵ-diamond distance, we can control the accumulation of errors by setting an increased accuracy goal of \(\rmpoly(\epsilon /(t\beta \parallel H\parallel ))\) for the approximate block encodings U, V. This results in an overall \(\mathcalO(\beta \sqrt\log (t\beta \parallel H\parallel /\epsilon ))\) and \(\mathcalO(\beta \log ^2(t\beta \parallel H\parallel /\epsilon ))\) (controlled) Hamiltonian simulation time overhead for implementing sufficiently accurate block encodings U and V, respectively.

Comparison with physically derived master equations

Our synthetic Lindbladian is mainly presented as an algorithmic construction. In this section, we compare it with physically motivated master equations derived from first-principles open-system calculations. Overall, we believe that our Lindbladian can serve as a self-contained toy model of thermalization. Nevertheless, for quantitative modelling of particular system–bath interactions, the role of strict detailed balance is less clear, and it may be preferable to use a physically derived master equation.

The textbook setup in open-system thermalization^24,59 considers a system governed by a Hamiltonian H_S that couples weakly to a large thermal bath with Hamiltonian H_B, which are together governed by the total Hamiltonian \(H_\rmtot=H_\rmS\otimes I_\rmB+I_\rmS\otimes H_\rmB+\lambda \sum _a\in AA^a\otimes B^a\). The Hermitian operators A^a: a ∈ A act on the system (mirroring our jump operators, hence the same notation) and B^a: a ∈ A acts on the bath, whereas λ represents the coupling strength. Tracing out the bath, we can obtain an effective master equation governing the system dynamics under the assumptions that the thermal bath is Markovian and the coupling λ is sufficiently weak.

The aforementioned Davies generator was originally derived in the weak-coupling limit λ → 0 (relative to all other energy scales). In this limit, the rotating-wave approximation (or the secular approximation) removes the cross terms \(A_\nu _1[\cdot ]A_\nu _2^\dagger \); this perfect isolation of Bohr frequencies causes the Davies generator to satisfy detailed balance, but at the same time, makes it implausible for many-body systems with exponentially small level spacings. To focus on issues related to detailed balance, here we studied only the simplest form of the Davies generator. In principle, different jumps A^a may have different transition weights, as they correspond to the Fourier transform of the bath correlation function \(\langle \rme^\rmiH_BtB^a\rme^-\rmiH_BtB^a\rangle \), but for algorithmic purposes, it is natural to use universal transition weights. Also, we have studied only the dissipative part of the Davies generator (equation (5)). However, the full Davies generator also includes a Lamb-shift term that somewhat resembles our coherent term, but depends on additional details of the bath correlation functions. As the Lamb-shift term commutes with the Hamiltonian, adding this term keeps the Gibbs state stationary.

Recently, there have been several attempts to derive more realistic master equations for many-body systems by avoiding the λ → 0 limit needed for the rotating-wave approximation. This essentially translates to introducing Lindblad operators with a finite energy uncertainty, or, equivalently, in the time domain, integrals over Heisenberg-evolved jump operators weighted by a finite-width window function. In particular, the coarse-grained master equation⁵⁹ takes a very similar form as ours (equation (7)), but its operator Fourier transform features a uniform integral \(\frac1\sqrt2\rm\pi T\int _-\fracT2^\fracT2\rme^\rmiHtA^a\rme^-\rmiHt\rme^-\rmi\omega t\rmdt\), and its coherent term also resembles ours (equation (19)) but does not seem to strictly enforce detailed balance. The universal Lindblad equation⁶⁰ combines (square root of) the transition weights into the operator Fourier transforms and is closer to subsequent constructions^61,62. Very recently⁶³ derived a master equation with exact KMS-detailed balance using slightly different operator Fourier transform weights compared with ours. All the above recent master equations feature some finite energy uncertainty, derived from various system–bath parameters, that parallels our tunable Gaussian width σ.