Early-twentieth-century cold bias in ocean surface temperature observations

Global mean temperature reconstruction method

To predict global temperature metrics from the LSAT or SST records with incomplete coverage, we invoked a regularized linear regression method known as ridge regression, a key tool in statistical learning²³. Training of the statistical models was based on climate model simulations from the CMIP6 archive⁵⁰ with complete coverage, from which we calculated the target metrics of the statistical model. In the main text, we focus on GMST as the target metric (that is, Y^GMST), but we also reconstructed global mean sea surface temperature (GMSST; Supplementary Fig. 3) and global mean land surface air temperature (GMLSAT; Supplementary Fig. 4). For the land data, we additionally reconstructed regional SSTs of the West Pacific (Fig. 4), Indian Ocean (Fig. 4) and West Atlantic (Fig. 4). The selected target metrics represent key metrics of global temperature change¹¹ and regional ocean temperature change for the comparison with ocean palaeoclimate reconstructions³³. Monthly coverage maps of non-infilled data were taken from the CRUTEM5 dataset for the LSAT record²⁴, and from HadSST4 for the SST record¹⁴. For each target metric and for both land and ocean, the conceptual reconstruction set-up was conducted using a linear statistical model that relates incomplete spatial LSAT or SST patterns to the respective target metric (Y_mod),

In equation (1), Y_mod represents a vector of length n (the number of training time steps in the multi-annual monthly time series) of the target metric we seek to reconstruct in climate models used for training. The respective climate models’ spatial patterns of LSATs or SSTs are stored in matrices X_mod of dimension n × (p + 1), and ϵ represents the error terms. Each row contains the spatial pattern for a given training time step (n in total), and each column contains the values of a given location (grid cell) as predictor (p spatial predictors in total, and an additional column of ones that account for the intercept). As SST and LSAT coverage varies over time, the training (equation (1)) is repeated for each monthly coverage mask from January 1850 to December 2020 as the statistical model contains a different number of predictors p for each monthly coverage mask. The training for each monthly coverage mask is based on 93 historical climate model simulations (covering the historical time period 1850–2014, or extended to 2020 where available, with in total n = 15.626 model-years, trained for each month separately) from the CMIP6 archive. During the training process, a vector of regression coefficients \(\widehat{{\boldsymbol{\beta }}}\) is estimated, representing a weight for each local SST or LSAT time series. Hence, the estimated regression coefficients seek a representation that optimally reconstructs the target metric from the available incomplete spatial pattern of the time series across the climate models used for training. The statistical model and reconstruction set-up is illustrated in Extended Data Fig. 1.

Specifically, for a given coverage mask, here, for example, June 1895, and for GMST as the target metric, the training of our statistical reconstruction model was set up for LSATs and SSTs as:

It is noted that despite the fact that the coverage is restricted to the June 1895 masks in this example, we still used all months of June in the full time period of 1850–2014 (partly extended to 2020) from the historical simulations of climate models for training the regression models (that is, the estimation of regression coefficients). For example, \({X}_{{\rm{mod}},{\rm{Land}}:1895{\rm{\mbox{–}}}06}\) has the dimensions n = 15.626 and (p + 1) = 297, as the land-coverage mask in CRUTEM5 has p = 296 non-missing values in June 1895.

After estimating the regression coefficients, we predicted each target metric at each time step based on SST or LSAT observational datasets, and the actual coverage. For example, for June 1895, LSAT and SST predictions of GMST would read as

where X_{CRUTEM5:1895-06} is now a 1 × (p_Land:1895-06 + 1) matrix that contains the actual CRUTEM5 data for June 1895, and \({\widehat{{\boldsymbol{\beta }}}}_{{\rm{CRUTEM5}}:1895\text{-}06}^{{\rm{GMST}}}\) is a vector of length (p_Land:1895-06 + 1, with p reflecting the number of grid cells that contain values in June 1895), which was obtained in the training step (equation (2)). By repeating this step analogously for all time steps from January 1850 to December 2020, we generated an observational reconstruction for each target metric and for the LSAT and SST record, for example, denoted for GMST as \({\widehat{{\bf{T}}}}_{{\rm{CRUTEM}}5}^{{\rm{GMST}}}\) and \({\widehat{{\bf{T}}}}_{{\rm{HadSST}}4}^{{\rm{GMST}}}\). The reconstruction target (GMST) is denoted as the superscript, and the origin of the observational dataset as the subscript. In a similar way, we achieved a reconstruction of each historical CMIP6 model simulation’s GMST by projecting masked temperature patterns on the respective regression coefficients (for example, \({\widehat{{\bf{T}}}}_{{\rm{CMIP}}6,{\rm{Land}}}^{{\rm{GMST}}}\) and \({\widehat{{\bf{T}}}}_{{\rm{CMIP}}6,{\rm{Ocean}}}^{{\rm{GMST}}}\)). We averaged the monthly output to annual means. This yielded a CMIP6 global temperature reconstruction that covers 1850–2020 based on only observed coverage, and thus provides a ‘like by like’ masked comparison with observations (in Fig. 2). The reconstruction as described above in equations (1)–(5) does not account for observational uncertainties and biases in the training process (‘no uncertainties and biases in training’).

Including observational biases and uncertainties in GMST estimation

Recent studies have used statistical or machine-learning algorithms, trained on climate model simulations, for optimal infilling of incomplete observations²⁶. State-of-the-art climate models indeed represent key modes of ocean–atmosphere variability and forced response patterns³⁰. Statistical and machine-learning algorithms thus typically assume that the training distribution (that is, climate models or reanalyses) and the testing distribution (observations) follow the same probability distribution²³. This is also assumed in the reconstruction method outlined in equations (1)–(5) above. However, the observed temperature record contains substantial measurement uncertainties and systematic biases, in both observed SSTs^6,15 and LSATs^13,24 (summarized in the main text), which climate models do not represent. If those uncertainties and biases were disregarded, our reconstruction algorithm would risk being ‘overfitted’—that is, too specifically tailored—to climate model simulated patterns and variability. Hence, it would probably perform rather poorly on observations, even if the relationship between local predictors and GMST was reproduced correctly in the climate model. This phenomenon is known as covariate shift in statistical learning⁵¹. For example, grid cells in the tropics often carry a high signal for estimating global-scale variability, but precisely those grid cells are sparse in the early observational record, and potentially affected by measurement uncertainties and biases. In addition to the reconstruction method described by equations (1)–(5), we account for measurement uncertainties and biases in our reconstruction by making use of the existing, comprehensive uncertainty and bias models for CRUTEM5 and HadSST4. In HadSST4, uncertainties are modelled in the form of three structurally different components^13,14: prevalent systematic errors with a complex temporal and spatial correlation structure (biases, denoted ϵ_b,Ocean(s, t)); systematic partially correlated errors from individual ships or buoys (ϵ_p,Ocean(s, t)); and uncorrelated errors from individual measurements or incomplete sampling of grid-boxes (ϵ_u,Ocean(s, t)); indices s and t reflect that the error terms vary in space and time, respectively. The three error terms are treated as statistically independent. The time–space systematic errors are represented by a 200-member ensemble that represents different realizations of these potential biases. Systematic errors from ships or buoys are represented by spatial error covariance matrices, and uncorrelated errors are estimated as gridded error fields.

In CRUTEM5, uncertainties are encoded following the method given in ref. ⁵². A 200-member ensemble of potential realizations of known, temporally and spatially correlated uncertainties in near-surface air temperature has been produced as part of the HadCRUT5 Noninfilled Data Set¹³ (that is, ϵ_b,Land(s, t)). The corresponding ensemble of CRUTEM5 LSAT anomalies has been extracted from this, using the HadSST4 ensemble to unblend SST and LSAT anomalies in coastal grid cells. The ensemble realization of biases encompasses uncertainties such as station-based homogenization errors and uncertainty in climatological normals, as well as regional urbanization errors and non-standard sensor enclosures (full description provided in refs. ^13,24,52). Uncorrelated uncertainties (measurement errors or incomplete sampling of grid cells) are available in the form of gridded error fields (that is, ϵ_u,Land(s, t)).

To take into account these comprehensive error structures, we adjust the matrices that store the appropriately masked model simulated SST or LSAT patterns (X_mod) for training by randomly adding one systematic error realization (ϵ_b(s, t)) of the HadSST4 or CRUTEM5 ensemble to each CMIP6 historical model simulation used for training. We further generate realizations of the uncorrelated gridded fields (ϵ_u(s, t)), for HadSST4 and CRUTEM5, and in addition a realization of the spatially correlated fields (ϵ_p,Ocean(s, t)) for HadSST4. Hence, for a specific coverage mask such as June 1895, we adjust each CMIP6 historical ensemble member in the training sample, obtaining:

From these perturbed climate model patterns, we train our statistical model as indicated in equations (2) and (3), that is, to optimally predict the simulated (unperturbed) target metric (\({{\bf{Y}}}_{{\rm{mod}}}^{{\rm{GMST}}}\)). This yields a new set of regression coefficients based on the perturbed data (\({\widehat{{\boldsymbol{\beta }}}}_{{\rm{Land}}:1895\text{-}06}^{* {\rm{GMST}}}\) and \({\widehat{{\boldsymbol{\beta }}}}_{{\rm{Ocean}}:1895\text{-}06}^{* {\rm{GMST}}}\)). By adding the error terms, the algorithm optimally predicts the target metric as in equations (1)–(5) while taking into account ‘real-world’ estimates of uncertainties and biases in the estimation of the regression coefficients. This results in lower coefficient weights for grid cells that are strongly affected by uncertainties and biases (Extended Data Fig. 2). Finally, following equations (4) and (5), we obtain observation-based reconstructions of each target metric (\({\widehat{{\bf{T}}}}_{{\rm{CRUTEM}}5}^{* {\rm{GMST}}}\) and \({\widehat{{\bf{T}}}}_{{\rm{HadSST}}4}^{* {\rm{GMST}}}\)), and analogously based on CMIP6 models (\({\widehat{{\bf{T}}}}_{{\rm{CMIP}}6,{\rm{Land}}}^{* {\rm{GMST}}}\) and \({\widehat{{\bf{T}}}}_{{\rm{CMIP}}6,{\rm{Ocean}}}^{* {\rm{GMST}}}\)). An ensemble of 200 observational reconstructed time series (\({\widehat{{\bf{T}}}}_{{\rm{CRUTEM}}5}^{* {\rm{GMST}}}\) and \({\widehat{{\bf{T}}}}_{{\rm{HadSST}}4}^{* {\rm{GMST}}}\)) is thus obtained, where the input for each reconstruction contains a different error realization. For ease of notation, we drop the asterisks in the main text, as all observations-based reconstructions are trained with bias and uncertainty realizations added to CMIP6, unless noted otherwise. For CMIP6 reconstructions (\({\widehat{{\bf{T}}}}_{{\rm{CMIP}}6,{\rm{Land}}}^{* {\rm{GMST}}}\) and \({\widehat{{\bf{T}}}}_{{\rm{CMIP}}6,{\rm{Ocean}}}^{* {\rm{GMST}}}\)), individual model members (without error realizations) generally serve as input for GMST reconstructions, with one exception: for the temporal correlations within single reconstructions shown in in Fig. 2d,e, model members are treated as observations, meaning a random error and bias realization is added to each model member. The reconstruction uncertainty ranges in Figs. 1 and 2 are based on the reconstructions ensembles obtained as described above (that is, conditional mean predictions based on our statistical models from 200 different bias and uncertainty realizations). An illustration of the performance of our statistical reconstruction on CMIP6 models based on sparse coverage (June 1895 for land and ocean, respectively), and more extensive coverage (June 1995 for land and ocean, respectively) is shown as Extended Data Fig. 3. An evaluation of the approach with and without uncertainties and biases is provided in Supplementary Information.

Statistical learning technique and cross-validation of statistical models

Equation (1) represents a linear regression problem with a relatively high dimensionality, where the number of predictors p can be substantial (for example, p > 1,000). Conventional methods such as ordinary least squares aim to minimize the residual sum of squares (\({\rm{R}}{\rm{S}}{\rm{S}}={\sum }_{i}^{n}{({{\bf{Y}}}_{i}-{X}_{{\bf{i}}}{\boldsymbol{\beta }})}^{2}\)). However, in high-dimensional settings, relying on this single objective may be problematic because regression coefficients lack proper constraints⁵³. To address such collinearity issues, we turn to ridge regression, a statistical learning technique designed for such scenarios^23,53. Ridge regression prevents overfitting by incorporating a penalty for model complexity through the shrinkage of regression coefficients. The shrinkage is based on the sum of squared regression coefficients (referred to as L2 regularization) and a ridge regression parameter λ that governs the degree of shrinkage. Consequently, ridge regression addresses a joint minimization problem expressed as

This results in small yet non-zero regression coefficients, and these coefficients are relatively evenly distributed among correlated predictors²³. The tuning parameter λ determines the extent of shrinkage and is determined through cross-validation, as discussed in the following paragraph. The intercept of the linear model is not shrinked.

Cross-validation

We used a standard cross-validation approach to determine the ridge regression parameter (λ) and to obtain the regression coefficients. Cross-validation is a common practice in data science, dividing the raw dataset into different, distinct folds. This ensures that model fitting and validation occur on distinct data subsets, preventing biased performance evaluations. In the context of climate science, the cross-validation method used here adopts a ‘leave one model out’ strategy, resembling an iterative perfect model approach. In this process, for a total of k CMIP6 models, the ridge regression model is iteratively fitted on k − 1 models and validated on the kth model (referred to as ‘leave-one-model-out cross-validation’). This iterative approach guarantees that the regression coefficients generalize effectively to an unseen model, ensuring the robustness of the statistical model across the CMIP6 multi-model archive. The tuning parameter λ is then selected during cross-validation to minimize the mean squared error on out-of-fold data, and the corresponding regression coefficients are extracted. The final set of regression coefficients is obtained as the average across the k model fits. As several climate models provide different numbers of ensemble members, we weight the regression such that each climate model receives equal weight for the extraction of regression coefficients.

Data pre-processing and observational data

For the gridded fields as regression predictors, we extracted the variables ‘tas’ (near-surface air temperature) and ‘tos’ (sea surface temperature) from climate model historical (1850–2014) and 2014–2020 simulations following the Shared Socioeconomic Pathway (SSP) 2-4.5 scenario that contributed to the CMIP6 multi-model archive⁵⁰. All simulations were regridded to a regular 5 × 5° longitude–latitude grid, which is identical to the CRUTEM5 and HadSST4 grid. All climate model data were centred based on a 1961–1990 reference period, in accordance with CRUTEM5 and HadSST4 data processing.

We computed the target metrics of our regression models as follows from the models’ native grids. Global mean surface air temperature (GSAT) is the area-weighted global mean of near-surface air temperature from the spatially complete gridded fields. Global mean surface temperature (GMST) is the blended area-weighted average of SSTs over ocean areas, and surface air temperatures over land areas and areas with sea ice. We follow a standard blending procedure⁵⁴, where blending is conducted based on the absolute temperature values (including sea-ice masks from CMIP6 models). GMSST and GMLSAT are determined analogously as the global area-weighted average of SSTs and LSATs, respectively. We also computed regional target metrics for the comparison of instrumental observations with palaeoclimate reconstructions, following ref. ³³. The tropical SST reconstruction target metrics cover the (area-averaged) Indian Ocean (20° N–15° S, 40–100° E, in total 25.5 × 10⁶ km²), western Pacific (25° N–25° S, 110–155° E, 26.9 × 10⁶ km²) and western Atlantic (15–30° N, 60–90° W, 5.1 × 10⁶ km²) oceans. All target metrics are centred based on the 1961–1990 reference period.

For the training of our regression models, we selected three historical ensemble members from each CMIP6 model, and the time period 1850–2020 (historical simulations and SSP2-4.5 simulations are concatenated up to 2020). The training dataset consisted in total of 15,626 model-years, and an overview of the CMIP6 models used for training is given in Supplementary Table 4. As the optimal reconstruction coefficients may vary seasonally, training of the regression models for each month m was based on monthly data only from the same month in CMIP6 models (that is, the 15,626 model-years correspond to 15,626 monthly training samples).

Once regression coefficients were extracted following the methodology described above, we obtained observation-based predictions for all target metrics by using the spatially incomplete CRUTEM5 and HadSST4 data as inputs to the regression models (equations (4) and (5)). The comparison of our observation-based reconstruction with CMIP6 models in Fig. 2 was based on 602 CMIP6 historical simulations that contain ‘tas’ and ‘tos’ data, that is, 98.835 model-years (overview in Supplementary Table 4), which were masked and reconstructed with observational coverage for each time step.

Additional observation-based reconstructions

The focus of this paper is to understand and compare the global temperature reconstructions obtained independently from the HadSST4 dataset¹⁴ and the CRUTEM5 LSAT dataset²⁴, which are both subject to varying incomplete coverage and affected by complex time-evolving uncertainties and biases. Both datasets and their uncertainties have been developed and maintained over decades^14,24, and both are key datasets that inform the Intergovernmental Panel on Climate Change process⁴. However, several other SST, LSAT and night-time marine air temperature datasets have been developed, and our goal is to compare those data on a ‘like by like’ basis with our reconstructions: we derived a land-based reconstruction using an alternative LSAT dataset (Berkeley Earth Land²⁷) instead of CRUTEM5 as the predictor. These reconstructions (\({\widehat{{\bf{T}}}}_{{\rm{BEST}}{\rm{\mbox{–}}}{\rm{land}}}\)) used the model trained with CRUTEM5 coverage, and a few missing grid cells were filled using nearest-neighbour interpolation. Berkeley Earth Land is based on the Global Historical Climatology Network Monthly Temperature Dataset⁵⁵, Version 4, with a much higher number of weather stations than CRUTEM5, and compares favourably to a recently homogenized land dataset¹⁸. Similarly, we used three alternative SST datasets (COBE-SST2⁵⁶, ERSST5⁵⁷ and an unadjusted version of HadSST4), and we projected all three datasets onto the regression coefficients obtained for the CMIP6 SSTs masked to HadSST4 coverage. COBE-SST2 and ERSST5 in general have larger coverage than HadSST4, but again a few missing grid cells were filled using nearest-neighbour interpolation.

In addition, we trained three global-scale reconstructions based on other datasets for comparison. We followed the reconstruction method outlined above but with different training and observational datasets. First, a reconstruction was trained on CMIP6 marine air temperatures (‘tas’ over the ocean), and the regression model was subsequently used to derive a reconstruction for observed night-time marine air temperature data (ClassNMAT²⁵; that is, reconstructions denoted \({\widehat{{\bf{T}}}}_{{\rm{ClassNMAT}}}\) in the main text). Second, we derived a reconstruction based on the CoastalHybridSST dataset⁷ (\({\widehat{{\bf{T}}}}_{{\rm{CoastalHybridSST}}}\)), that is, a SST dataset with corrections derived from co-located coastal weather stations. The training steps were identical to the training of HadSST4, but using the coverage masks from HadSST3 (on which the ‘CoastalHybridSST’ dataset is based) and its uncertainties. Third, we trained our regression models on CMIP6 data masked to HadSST4 coverage as above, but with the global mean removed individually for each time step. We subsequently used this regression model with HadSST4 with the global mean removed at each time step as predictors (shown in Supplementary Fig. 5). This approach is similar to ref. ⁵⁸, and allows to test whether large-scale atmosphere–ocean climate variability (which is still largely present if the global mean at each time step is removed) may explain part of the cold anomaly. A full overview of all reconstructions analysed in this paper is provided in Supplementary Table 1, and an overview of the gridded datasets in Supplementary Table 2.

In addition, we compared our observational GMST reconstructions to several widely used blended GMST datasets (Extended Data Fig. 4). In addition, we used the machine-learning method for climate reconstructions by ref. ²⁶ as an independent technique to evaluate and compare the main method of this study (without including estimates of uncertainty and biases at training time) (Extended Data Fig. 4a). Similarly to above, CMIP6 historical experiments were trained with the missing value masks of HadSST4 and CRUTEM5. Subsequently, each observational dataset was infilled by the convolutional neural network using partial convolutions and an updated mask mechanism. An overview over all observational datasets used is provided in Supplementary Table 3.

Palaeoclimate data

We compared our reconstructions with two palaeoclimate reconstructions (Supplementary Table 3).

First, we analysed a reconstruction of annual GMST that uses the PAGES 2k temperature multi-proxy data collection³² (version 2.0.0) as presented in ref. ¹². The proxy records undergo screening based on regional temperature, resulting in a subset of 257 records, of which 81% are from trees or corals. The calibration period spans ad 1850–2000, and calibration is based on the Cowtan–Way kriging interpolated HadCRUT4 dataset¹⁹. Various reconstruction methods are used to reconstruct 2,000 years (ad 1–2000) of annual GMST: composite plus scaling (CPS), principal component regression (PCR), M08⁵⁹ (based on a regularized expectation maximization algorithm), pairwise comparison (PAI), the OIE method (derived from CPS but with more comprehensive uncertainty estimation), BHM (a statistical model of GMST depending on external forcing and additive noise), and DA (fusing proxy records and climate model simulations). Four methods (CPS, PCR, BHM and DA) are based on only annually resolved proxies, whereas the other three methods also include low-frequency proxies. Each method generates an ensemble of 1,000 GMST reconstructions for uncertainty quantification; thus, in total, 7,000 ensemble members that cover different proxy types and different statistical reconstruction methods. Method-specific details and adaptations, as well as an evaluation and discussion of uncertainties, are outlined in ref. ¹².

Second, we analysed a regional SST reconstruction³³, which is based on only ocean proxy records. The ocean proxy records are derived exclusively from annually or seasonally resolved tropical coral archives. Temperature estimation is based mainly on oxygen isotopic composition (δ¹⁸O of coral carbonate), but records based on the skeletal Sr/Ca ratio and coral growth rate are also included. Reconstruction targets are regionally averaged tropical SST anomalies at the annual timescale for four large-scale ocean basins: the western Atlantic, the eastern Pacific, the western Pacific and the Indian Ocean. The study uses a weighted CPS approach, using a nesting procedure to address the changing number of available observations over time. Palaeoclimate proxies are not screened, but weighted. Each record’s contribution to the composite is scaled by its relationship with instrumental target SST anomalies, considering both magnitude and significance of variance. An ensemble of reconstructions accounts for uncertainties in the CPS method, different weighting schemes and calibration periods. The ‘best’ reconstruction is selected based on the highest cumulative reduction of error score over the validation period. Finally, we analysed individual palaeoclimate proxies in Extended Data Fig. 6 and Supplementary Information.

Analysis methods and evaluation metrics

Timescale separation and attribution

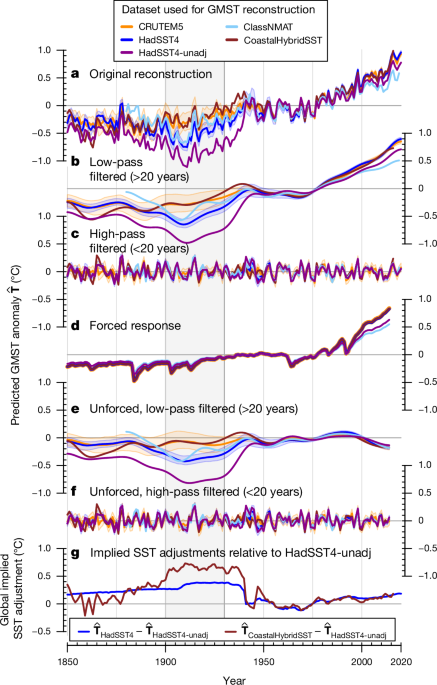
To analyse our GMST reconstructions, we apply a timescale filtering and an attribution method in Fig. 1. We use a low-pass Butterworth filter with a period of 20 years to separate our original reconstruction in a low-pass filtered and high-pass filtered time series (Fig. 1b,c) based on the R package ‘dplr’⁶⁰.

To further analyse forced and unforced components of the reconstructions, we apply an attribution method²⁸ for global mean temperature. The reconstructed \({\widehat{{\bf{T}}}}^{{\rm{GMST}}}\) (or other target metric) is regressed on the multi-model mean of CMIP6 in the 1850–2014 time period (that is, the ‘forced response’ of the CMIP6 multi-model mean in historical simulations). Internal variability is assumed to follow a simple stochastic AR(1) process, which conceptually represents atmospheric white noise dynamics that force a damped and slower system of the oceans²⁸. The regression model is solved following the Hildreth–Lu method⁶¹. The scaled forced responses for the different reconstructions are shown in Fig. 1d, and unforced residual components in Fig. 1e,f. All data processing and statistical computations as well as figures were created using the R software for statistical computing, version 4.2.2 (ref. ⁶²). For creating the maps in Fig. 3 and Extended Data Figs. 1, 2 and 6, we used the ‘sp’^63,64 and ‘raster’⁶⁵ packages. The land contours and country polygons of the figures that show maps were obtained from Natural Earth (naturalearthdata.com).

Evaluation metrics and constraints on ocean warming

Several evaluation metrics are derived from our land- and ocean-based reconstructions, and we compare those with climate models and palaeoclimate reconstructions:

• Temperature difference of ocean- versus land-based GMST reconstruction. We analysed the difference between the ocean- and land-based reconstructions at each time step for a given target metric, \(\Delta {\hat{{\bf{T}}}}_{{\rm{O}}\text{-}{\rm{L}}}^{{\rm{G}}{\rm{M}}{\rm{S}}{\rm{T}}}={\hat{{\bf{T}}}}_{{\rm{H}}{\rm{a}}{\rm{d}}{\rm{S}}{\rm{S}}{\rm{T}}4}^{{\rm{G}}{\rm{M}}{\rm{S}}{\rm{T}}}-{\hat{{\bf{T}}}}_{{\rm{C}}{\rm{R}}{\rm{U}}{\rm{T}}{\rm{E}}{\rm{M}}5}^{{\rm{G}}{\rm{M}}{\rm{S}}{\rm{T}}}\). The observationally derived \(\Delta {\widehat{{\bf{T}}}}_{{\rm{O}}\text{-}{\rm{L}}}^{{\rm{GMST}}}\), including the error realizations, was compared with the equivalently masked reconstruction range of ocean and land temperatures in the CMIP6 models (\(\Delta {\widehat{{\bf{T}}}}_{{\rm{O}}\text{-}{\rm{L}},{\rm{CMIP}}6}^{{\rm{GMST}}}\)), and shown in Fig. 2 along with a low-pass and a high-pass filtered version.

• Pearson correlation between ocean- and land-based reconstructions. We calculated the Pearson correlation between the original land and ocean reconstructions (\(r({\hat{{\bf{T}}}}_{{\rm{H}}{\rm{a}}{\rm{d}}{\rm{S}}{\rm{S}}{\rm{T}}4}^{{\rm{G}}{\rm{M}}{\rm{S}}{\rm{T}}},{\hat{{\bf{T}}}}_{{\rm{C}}{\rm{R}}{\rm{U}}{\rm{T}}{\rm{E}}{\rm{M}}5}^{{\rm{G}}{\rm{M}}{\rm{S}}{\rm{T}}})\)) and for the high-pass filtered versions in a 50-year moving window. We compared the time series of \(r({\hat{{\bf{T}}}}_{{\rm{H}}{\rm{a}}{\rm{d}}{\rm{S}}{\rm{S}}{\rm{T}}4}^{{\rm{G}}{\rm{M}}{\rm{S}}{\rm{T}}},{\hat{{\bf{T}}}}_{{\rm{C}}{\rm{R}}{\rm{U}}{\rm{T}}{\rm{E}}{\rm{M}}5}^{{\rm{G}}{\rm{M}}{\rm{S}}{\rm{T}}})\) with the range of Pearson correlations obtained from reconstructions of CMIP6 model simulations (\(r({\hat{{\bf{T}}}}_{{\rm{O}}{\rm{c}}{\rm{e}}{\rm{a}}{\rm{n}},{\rm{C}}{\rm{M}}{\rm{I}}{\rm{P}}6}^{{\rm{G}}{\rm{M}}{\rm{S}}{\rm{T}}},{\hat{{\bf{T}}}}_{{\rm{L}}{\rm{a}}{\rm{n}}{\rm{d}},{\rm{C}}{\rm{M}}{\rm{I}}{\rm{P}}6}^{{\rm{G}}{\rm{M}}{\rm{S}}{\rm{T}}})\)) masked and processed in the same way as observations, including observational error realizations, in Fig. 2.

• Turn-of-the-twentieth-century temperature change (1901–1920 averages compared with 1871–1890 averages). Because ocean-derived temperatures deviate from the land-derived temperatures from the 1890s onwards, we compared the multidecadal period before the ocean cold anomaly (1871–1890) with a period during the cold anomaly (1901–1920). We computed multidecadal temperature changes around the turn of the twentieth century as the difference between temperature averages in both periods, \(\Delta {\widehat{{\bf{T}}}}^{{\rm{GMST}}}=\overline{{\widehat{{\bf{T}}}}_{1901-1920}}-\overline{{\widehat{{\bf{T}}}}_{1871-1890}}\). These temperature differences are computed for co-located coastal SST and LSAT data (Fig. 3), and for the global reconstructions and palaeoclimate reconstructions (Fig. 4). A t-test for significant differences between co-located coastal land and coastal marine grid cells was conducted for all large-scale regions shown in Fig. 3c.

• Emergent constraints on SST trends. We derived emergent constraints on global mean SST trends in the period 1871–1910 (ocean cooling) and for the early-twentieth-century-warming period (1901–1940). Constraints were derived based on HadSST4 (\({\widehat{{\bf{T}}}}_{{\rm{HadSST}}4}^{{\rm{GMSST}}}\)) and the CoastalHybridSST dataset⁷ (\({\widehat{{\bf{T}}}}_{{\rm{CoastalHybridSST}}}^{{\rm{GMSST}}}\)), as well as from land temperature change based on CRUTEM5 (\({\widehat{{\bf{T}}}}_{{\rm{CRUTEM}}5}^{{\rm{GMLSAT}}}\)), and based on the PAGES 2k GMST reconstructions and the Ocean2k tropical SST reconstruction. We related all datasets to global mean SST trends using an emergent constraint technique⁴⁴ explained in the next paragraph.

Derivation of observational constraints on historical ocean warming

In Fig. 5, we constrained the ranges of global mean SST trends in the 1871–1910 and 1901–1940 periods using the different observation-based datasets (longer periods, 1871–1920 and 1901–1950, are shown additionally in Supplementary Fig. 8). To derive those uncertainty ranges, we applied the method of emergent constraints⁴⁴, which uses the relationship between an observable metric (predictor metric) and a target metric across an ensemble of climate model simulations to constrain the target metric based on the observable climate metric. In our application, the predictor metrics and the target metric consisted of temperature trends from the same time period but for different large-scale regions. Our target metric in Fig. 5 was the GMSST trend in the periods 1871–1910 and 1901–1940, respectively. The predictor metrics were the predicted GMSST trends (\({\widehat{{\bf{T}}}}^{{\rm{GMSST}}}\)) for the HadSST4 and CoastalHybridSST datasets, predicted GMLSAT trends (\({\widehat{{\bf{T}}}}^{{\rm{GMLSAT}}}\)) for CRUTEM5, GMST (\({\widehat{{\bf{T}}}}^{{\rm{GMST}}}\)) for the PAGES 2k reconstructions, and tropical mean SSTs as the weighted average across the tropical Ocean2k regions³³. We first verified that CMIP6 historical simulations (including individual ensemble members to capture internal variability) show a strong linear relationship between our target metric and the respective predictor metrics. We found that relationships are linear with Pearson correlations of temperature trends of \(r({{\bf{T}}}^{{\rm{G}}{\rm{M}}{\rm{S}}{\rm{S}}{\rm{T}}},{\hat{{\bf{T}}}}^{{\rm{G}}{\rm{M}}{\rm{S}}{\rm{S}}{\rm{T}}})=0.98\), \(r({{\bf{T}}}^{{\rm{G}}{\rm{M}}{\rm{S}}{\rm{S}}{\rm{T}}},{\hat{{\bf{T}}}}^{{\rm{G}}{\rm{M}}{\rm{L}}{\rm{S}}{\rm{A}}{\rm{T}}})=0.84\), r(T^GMSST, T^TMSST) = 0.82, and r(T^GMSST, T^GMST) = 0.96 in the 1901–1940 period across the CMIP6 historical simulations. The linearity between land and ocean warming is expected from physical theory⁴³. Second, we used least-squares linear regression to derive prediction intervals for our target metric based on each individual predictor metric, following ref. ⁴⁴. Linear regression between two univariate variables y and x is given by y = β₁x + β₀ + ϵ, where β₁ is the regression slope and β₀ is the intercept. Least-squares linear regression minimizes the least-squares error

where N is the number of available samples. The minimization yields an estimate of the regression slope, \(\widehat{{\beta }_{1}}=\frac{{\sigma }_{xy}^{2}}{{\sigma }_{x}^{2}}\), where \({\sigma }_{xy}^{2}\) and \({\sigma }_{x}^{2}\) are the covariance between x and y, and the variance of x, respectively. The ‘prediction error’ of linear regression is given by⁴⁴:

Hence, for an observations-based temperature trend (x_obs), we predict the mean conditional GMSST trend as \({\widehat{y}}_{{\rm{obs}}}={\beta }_{1}{x}_{{\rm{obs}}}+{\beta }_{0}\), and we obtain the 2.5th to 97.5th percentile prediction ranges as \({\widehat{y}}_{{\rm{obs}}}\pm 1.96{\sigma }_{f}\). In cases where observational uncertainty estimates are available as an ensemble (x_obs,i, we derived the mean conditional GMSST trend as above for each member i of the observational ensemble (with n_ens denoting the ensemble size), and subsequently we sample for each member k = 100 times from a Gaussian distribution (\({\mathcal{N}}(\mu ={\widehat{y}}_{{\rm{obs}},i},{\sigma }^{2}={\sigma }_{f}^{2})\)) to capture the prediction uncertainty around each ensemble member \({\widehat{y}}_{{\rm{obs}},i}\). Finally, we obtain the constrained range of GMSST trends as the empirical 2.5th and 97.5th percentiles across the n_ens × k samples. The obtained prediction ranges thus account for internal variability in the relationship between our respective predictor metrics and our target metric.

Implications of early-twentieth-century global ocean cold anomaly for unforced variability estimates

In the main text, we discuss the implications of the ocean cold anomaly for the early-twentieth-century land and ocean warming, including the apparent ocean cooling before and up to around 1910 that is not supported by the land data. An additional aspect that requires attention in future work is the representation of decadal-to-multidecadal variability in models and observations. Some long-standing concerns have been raised that climate models may underestimate the magnitude of multidecadal variability at global or subglobal scales^66,67,68, whereas others argue that global-scale temperature variability on interannual to centennial timescales is plausibly represented^{12,69,70,71,72,73}. Yet, the range of unforced interdecadal variability in CMIP6 models is large⁷⁴. Recent studies have found that global temperature variability is well explained by known anthropogenic and natural forcings, but the cold anomaly in the early twentieth century remains a marked cold residual^2,3. If the ocean cold anomaly arises partly owing to uncorrected SST biases, it would imply improved agreement between models and observations in the instrumental period, and thus a smaller role for internal unforced variability than previously thought owing to a reduced cold residual in the early twentieth century^2,3.