3D printer assembly
Version 1
The DIP system components were mounted on two orthogonal optical breadboards to ensure precise alignment of the vertical and horizontal components (Supplementary Information section 1 and Supplementary Fig. 2a). Cross-sectional images were captured using a high-power projection module (LRS-WQ, Visitech) with a resolution of 2,560âÃâ1,600âpixels and a pixel size of 15.1âμm. The projection module and print head were positioned in the z direction using a 100âmm linear stage (MOX-02-100, Optics Focus) affixed to the vertical breadboard. The position of the airâliquid interface was controlled by a 50âml syringe connected to the print head with a silicone tube and pressurized using a 50âmm linear stage (MOX-02-50, Optics Focus). Two further linear stages (MOX-02-100, Optics Focus) enabled precise positioning of the cuvette or well plate for sequential or multi-step printing. Motion control was managed using a commercially available 3D printer control board (BIGTREETECH, SKR 3) with a custom DB9 breakout board. Orthogonal videos of the printing process were captured with a 4K CCD camera (AmScope, HD408) equipped with a 16âmm lens (Raspberry Pi, RPI-16MM-LENS).
Version 2
A second system iteration was developed for in situ imaging, with modifications to allow the printing container to move relative to a stationary probe (Supplementary Fig. 3). The system incorporated a custom CoreXY motion system and a NEMA 23 ball-screw linear stage to translate the entire CoreXY stage relative to the stationary print head. In situ imaging was facilitated by a blue reflective dichroic mirror (35-519, Edmund Optics) and a 50:50 beam splitter for illumination (43-359, Edmund Optics). Illumination was provided either coaxially or with a custom well-plate holder with a red collimated backlight. To maintain physiological temperatures and sterility during printing, the motion components and print head were enclosed within a custom heated chamber. Sterility was maintained by continuous HEPA filtration during printing, surface sanitization with 70% ethanol and sterilization with UV-C before use.
Print head
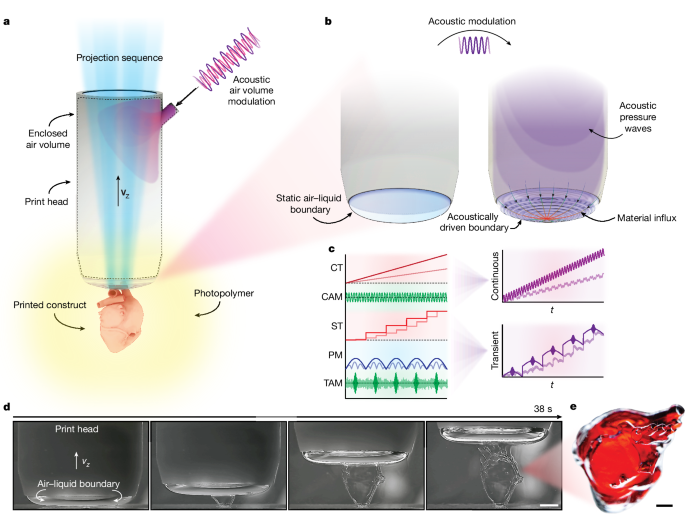
In this study, the size of the print head was tailored contingent upon the desired dimensions of the resin container. For almost all configurations, we used axisymmetric cylindrical print heads to simplify the computation of the interface shape, although other (arbitrarily shaped) print-head boundary contours were feasible as demonstrated. For more complex print-head topologies resulting in complex interface shapes, numerical methods such as Surface Evolver54 or SE-FIT55 can be used. Here, we used print heads ranging from 30 to 5âmm. An objectâs extent in the x and y directions was limited by the projectorâs total field of view at the focal plane. Additionally, an objectâs height was limited by the length of the print head, which was intrinsically coupled to the projection focal length and the ratio of the container volume to the volume displaced by the print head. For our set-up, the total submergible print-head length was approximately 70âmm. Note that much taller structures are conceptually feasible by submerging the projection and illumination optics or by increasing the working distance of the projection system. The print head was fabricated using a commercial 3D printing system (Form 3+, Formlabs). The print heads have an SM2 threaded insert, which allows us to quickly interchange print heads in version 2 of the system. A glass window was clamped between a gasket and the top of the print head to maintain an airtight enclosed volume while facilitating the transmission of light down its centre (Supplementary Fig. 1a,b). The print head also included an internal channel to enable gas to be delivered into the print-head cavity through the syringe system and acoustic modulation device. This port was used to either maintain or modulate the shape of the airâliquid interface during printing.
Acoustic modulation device
Acoustic modulation of the airâliquid interface was achieved by direct volume manipulation of the air volume within the print head. Conceptually, the approach was straightforward. The set-up consisted of a 3âinch 15âW voice coil driver (Techbrands, AS3034) affixed to an enclosed 3D printed manifold containing an inlet and outlet port (Fig. 3a and Supplementary Information section 2 and Supplementary Fig. 1c,d). The voice coil was driven by a commercially available amplifier (Adafruit, MAX9744) using the supplied auxiliary port, with specified waveforms sent by the MATLAB GUI. The frequency ranged between 1 and 500âHz when possible, with fixed or transient frequency or amplitude switching. By specifying a waveform for each degree of freedom, it was straightforward to synchronize the acoustic modulation with the remainder of the motion, optical and pressure control (Fig. 1c).
Material composition and preparation
PEGDA materials
Various concentrations of PEGDA were used in this study, ranging from 10% to 100%âw/v. For each formulation, we followed the same protocol. The required weight fraction of PEGDA Mn 700 (455008, Sigma) was dissolved in the corresponding volume fraction of 40â°C deionized water (excluding 100%âw/v) and thoroughly mixed for 10âmin. Subsequently, 0.035âw/w% of tartrazine (T0388, Sigma) and 0.25%âw/w of LAP (900889, Sigma) were added to the mixture and stirred until complete dissolution. The materials were then stored in light-safe Falcon tubes until required.
HDDA material
A solution of 500âmg of phenylbis(2,4,6-trimethylbenzoyl) phosphine oxide (511447, Sigma) and 50âg of 1,6-hexanediol diacrylate (246816, Sigma) was prepared by warming the mixture to 40â°C and stirring for 30âmin. To control the resolution in the z direction, the photo-absorber Sudan I (103624, Sigma) was added in various quantities ranging from 0 to 0.04%âw/w. The materials were then stored in light-safe Falcon tubes until required.
GelMA material
GelMA was synthesized following a previously reported protocol56, yielding a degree of substitution of 93% (confirmed by nuclear magnetic resonance). A 10%âw/v GelMA solution was prepared by dissolving 1âg of GelMA in 10âml of cell culture media (Freestyle 293 Expression Medium, Thermofisher) preheated to 37â°C. After complete dissolution of the GelMA, 3.5âmg of tartrazine and 25âmg of LAP were added to the solution, which was maintained at 37â°C until complete dissolution. The mixture was sterilized by passing it through a 0.22âµm sterile filter within a biosafety cabinet and subsequently stored in refrigerated light-safe Falcon tubes until required.
Alginate material
Norbornene-functionalized sodium alginate was synthesized based on a previously reported protocol57. In short, 10âg of sodium alginate were dissolved in 500âml of 0.1âM 2-(N-morpholino) ethane-sulfonic acid buffer (145224-94-8, Research Organics) and fixed to pH 5.0. Then, 9.67âg of 1-ethyl-3-(3-dimethylaminopropyl) carbodiimideâ¢HCl, 2.90âg of N-hydroxysuccinimide and 3.11âml of 5-norbornene-2-methylamine were added. The pH was fixed at 7.5 with 1âM NaOH. The reaction was carried out at room temperature for 20âh. The mixture was dialysed against water for 5âd before lyophilization. The degree of norbornene functionalization was determined to be 16.2% by 1H nuclear magnetic resonance. A 7%âw/v sodium alginate solution was prepared by dissolving 1âg of the sodium alginate in 14.29âml of phosphate-buffered saline solution. Next, 5âmg of tartrazine, 36âmg of LAP and 122.7âµl of 2,2â²-(ethylenedioxy)diethanethiol were dissolved in 5.59âml of phosphate-buffered saline, added to the sodium alginate solution and mixed until it was homogeneous. The pH was adjusted with 1âM NaOH until the solution was visibly opaque.
Diurethane dimethacrylate (UDMA) support material
A solution of 50âmg of phenylbis(2,4,6-trimethylbenzoyl) phosphine oxide (511447, Sigma) and 5âg of diurethane dimethacrylate (436909, Sigma) was prepared by warming the mixture to 45â°C and stirring for 30âmin. To remove trapped air bubbles, the mixture was transferred to a light-safe Falcon tube and centrifuged at 4,000ârpm for 10âmin to remove residual air bubbles.
Cell printing
Human embryonic kidney 293-F cells (Freestyle 293-F, Thermo Fisher) were used in a preliminary determination of the cell viability of the DIP 3D printing system. In this work, a cell solution with 7.2 million cells per millilitre was used for both the model of the kidney and the cell-viability measurements. To determine cell viability, a thin 500âµm wall (5âmmâÃâ0.5âmmâÃâ10âmm) was printed to minimize the effect of cell death due to insufficient media diffusion, which was imaged using a live/dead viability/toxicity kit (L3224, Invitrogen). Three structures were printed (nâ=â3), and measurements were taken after 24âh to determine the preliminary viability of the technique. Cell viability was determined at three locations for each sample (sâ=â3), with the total viability being an average of all collection points (Supplementary Fig. 18).
To create the cell-loaded bioink, the GelMA solution was warmed to 37â°C followed by the resuspension of cells into the solution. The solution was passed through a cell strainer (0877123, Thermo Fisher) and stored in a water bath at 37â°C when not in use. The printing process involved pipetting approximately 3âml of the GelMA ink into a single well of a 12-well plate and lowering the print head into the well. During each print, acoustic modulation (50âHz, Pâ=â0.3) was used to homogenize the suspension and mitigate cell settling. As the printed wall had a high aspect ratio and low contact area, a relatively slow print velocity of Vzâ=â150âµmâsâ1 was used to mitigate unwanted detachment. This resulted in an object creation time of approximately 30âs.
Data preprocessing, printing and postprocessing
Three-dimensional design models of Bowmanâs capsule, a tri-helix structure and a Kelvin cell were created using nTop. Tricuspid, heart and buckyball models were downloaded from Thingiverse.com. For each geometry, the STL file was extracted and sliced using Chitubox into a stack of PNG images. As the frame rate of the HDMI signal was limited to 120 frames per second (fps), we commonly used projection frame rates that matched the acoustic driving frequencies to minimize motion blurring. The object was discretized into a voxel array according to the desired linear print speed and frame rate. The layer height (Lh) was determined as \({L}_{{\rm{h}}}={v}_{z}/f\), where vz is the linear print speed and f is the acoustic excitation frequency, which matched the projection frequency. The image stack was further corrected using the convex-slicing algorithm to produce a secondary optimized image stack, with the sequence being sent to the projector over HDMI using Psychtoolbox-3 (ref. 58). The print sequence started by moving the print head to a defined distance above the print surface (or high-density material). The interface was then automatically brought coplanar with the image plane contingent on the selected print head. The MATLAB GUI was operated by first sending a signal to turn on the LED module and subsequently controlling the location of the airâliquid interface by modulating the pressure, acoustic driving and translation location. The optical power of the projection module was automatically set depending on the selected print velocity using the parameter space matrix. For prints made with HDDA, the printed structures were removed from the print volume and washed with isopropyl alcohol. For soft structures made from PEGDA and GelMA, the excess material was gently removed using a pipette (and recycled if PEGDA) and resuspended in deionized water or cell culture media to remove unpolymerized material. If required, the structures were fluidically detached from the bottom of the container and stored in an appropriate solution.
Convex-slicing algorithm
The developed convex-slicing algorithm aims to correct for geometrical discretization differences between a traditionally flat construction surface and the curved surface used in this work. A detailed explanation of the convex-slicing process is given in the Supplementary Information. However, the main components will be briefly restated here. First, the general shape of the interface was determined by the YoungâLaplace equation, \(\Delta p=-\,\gamma \nabla \cdot \widehat{n}\), which describes the Laplace pressure difference (\(\Delta p\)) sustained across a gasâliquid boundary dependent on the material surface tension (\(\gamma \)) and surface normal (\(\hat{n}\)). Here, we used axisymmetric print containers such that \(\hat{n}\) can easily be found by substituting the general expressions for principal curvatures. The capillary length \(l=\sqrt{\gamma /\rho g}\), where γ is the material surface tension, Ï is the material density and g is the acceleration due to gravity, was used to normalize the radial and vertical coordinates of the interface as \(x=r/l\) and \(y=z/l\). The resulting ordinary differential equation for the interface shape was \(\frac{{y}^{{\prime\prime} }}{{(1+{({y}^{{\prime} })}^{2})}^{3/2}}+\frac{{y}^{{\prime} }}{x{(1+{({y}^{{\prime} })}^{2})}^{1/2}}-y=0\).
This equation can be readily solved using numerical integration with appropriate boundary conditions (Supplementary Information section 4). However, using this method would require numerical integration for the steady-state case, and moreover, we would need to solve each intermediate state during compression with the associated boundary conditions. We, instead, opted to approximate the solution using cubic Bézier curves for the steady-state case and approximating the compressed profiles by geometrically deforming the Bézier curve while ensuring volume equivalency (Supplementary Information section 7). This is computationally faster given the large number of intermediate surfaces within the transient region. To convert the 2D Bézier solution into a 3D surface, the half-profile was revolved about the print headâs central z axis (Supplementary Information section 5). This produced a sequence of surfaces starting at the compressed state and transitioning to the steady-state interface profile. The corresponding convex projection(s) were determined by minimizing the Euclidean distance between the Cartesian voxel grid and the surface arrays (Supplementary Information section 6). Reconstruction accuracy was validated by âreplayingâ the projections over an empty voxel array and computing the Jaccard index between the reconstructed voxel array and the input voxel array (Supplementary Information sections 8 and 9).
Optical modelling
To determine our theoretical optical model (Supplementary Information section 10), we employed a similar approach to Behroodi et al.59, who modelled the in-plane resolution as the spatial convolution of the point spread function (\({\rm{PSF}}(x,y)\)) and the micro-mirror spatial arrangement (\(f(x,y)\)), where \(f\left(x,y\right)\ast {\rm{PSF}}\left(x,y\right)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }f({\tau }_{1},{\tau }_{2})\,\cdot \,{\rm{PSF}}\left(x-{\tau }_{1},y-{\tau }_{2}\right)\,{\rm{d}}{\tau }_{1}\,{\rm{d}}{\tau }_{2}\), and Ï1 and Ï2 represent spatial shifts, summed over all possible displacements, during convolution. To determine the effective delivered energy and depth of cure across the meniscus, a ray incident on the meniscus was decomposed into reflective and transmissive components, described by a transmissive efficiency η, dependent on the relative angle and refractive index mismatch \(\eta ({n}_{1},{n}_{2},\hat{{\bf{u}}},\hat{{\bf{n}}})\). Here, n1 and n2 represent the refractive index of the air and liquid, respectively, and \(\hat{{\bf{u}}}\) is the normal vector at a given point on the meniscusâs surface. The energy intensity along the transmissive vector \({\gamma }_{z}\) was approximated as a material-dependent BeerâLambert decay \({\mathcal{H}}({{\boldsymbol{\gamma }}}_{x},{{\boldsymbol{\gamma }}}_{y},{{\boldsymbol{\gamma }}}_{z})\,=\,\eta ({n}_{1},{n}_{2},\hat{{\bf{u}}},\hat{{\bf{n}}})\cdot \hat{{\bf{E}}}\,\exp \left(\frac{-{{\boldsymbol{\gamma }}}_{z}}{{\varepsilon }_{{\rm{d}}}\left[D\right]+{\varepsilon }_{{\rm{i}}}\left[S\right]}\right)\) (Supplementary Information section 11), where, εd and εi are molar absorption coefficients of the photoinitiator and the light absorber, respectively, and D and S are the concentrations of the photoinitiator and light absorber of the photopolymer resin, respectively. As the interface is curved, the effective resolution is spatially dependent on the local height of the meniscus relative to the focal plane. For each pixel at the focal plane, we mapped its local coordinate to the corresponding coordinate on the meniscus surface, resulting in a contour map of the effective pixel size across the interface. This map was used to theoretically predict the accurate area fraction the contingent on print headâs size and material properties (Supplementary Information section 12).
Acoustically driven flow
Analytical solution
To understand the formation of acoustically driven capillary-gravity waves, we used many established analytical approaches that describe the induced velocity and secondary streaming effects32 created by the meniscus (Supplementary Information sections 13â15). This analysis, therefore, establishes the velocity scaling laws for capillary-gravity waves dependent on the dominance of capillary- or gravity-driven effects. The dispersion relation for capillary waves, \({\omega }^{2}=\frac{\gamma }{\rho }{k}^{3}+{gk}\), relates the wave frequency (Ï) to the wavenumber (k). We, therefore, show that \({(\lambda /{l}_{{\rm{cap}}})}^{2}\) is a unitless quantity that relates the dominance of surface tension and acoustic parameters on the flow magnitude (Supplementary Information section 14). Here, lcap denotes the capillary length of the material. Thus, the flow velocity U scales as \(U\propto \frac{{h}_{0}^{2}\rho g\phi }{\lambda \mu }\) for \((\lambda /{l}_{{\rm{cap}}}) > 1\) and \(U\propto \frac{{h}_{0}^{2}\gamma \phi }{{\lambda }^{3}\mu }\) for \((\lambda /{l}_{{\rm{cap}}}) < 1\), where, h0, Ï and μ represent the surface perturbation, wave amplitude and viscosity, respectively. Supplementary Fig. 19 shows the effect of material and acoustic parameters on velocity scaling.
Experimental investigation
PIV was employed to understand the 3D flow field produced below the airâliquid boundary under acoustic excitation. A high-speed camera (Kron Technologies, Chronos 1.4 Camera) was used to capture footage of 20â50âµm poly(methyl methacrylate) particles during excitation, both normal and orthogonal to the airâliquid boundary. Particle tracing and velocity reconstruction were performed on the captured video sequences using PIVLab (ref. 60) for MATLAB. The exact parameters and methodology used can be found in Supplementary Information section 18. The velocity profiles for top-down and side are shown in Fig. 3câe and Supplementary Figs. 8 and 9.
Interface restabilization
To determine the transient interface restabilization in the bulk flow, high-speed photography under a uniform backlight was captured at 5,000âfps (Supplementary Fig. 7). Restabilization was determined by segmenting the meniscus edge and tracking the minimum y pixel location of the video stream during excitation and subsequent stabilization. The interface settling time was determined by applying an exponential criterion set at 1/e2 of the starting amplitude.
Image analysis of the material influx rate
The material influx rate with and without acoustic excitation was determined by filling a glass cuvette with materials doped with black dye to prevent light transmission. The cuvette was placed on top of a red backlight, such that when the airâliquid boundary formed against the base of the cuvette, the transmitted light was observed by a CCD (Supplementary Information section 19). The material influx rate was measured by raising the airâliquid boundary with and without acoustic excitation and tracking the influx of dyed material, which occluded the backlight transmission (Fig. 3f and Supplementary Information section 20 and Supplementary Fig. 11).
Print parameter space
To identify the ideal parameter space for DIP, a range of print speed and optical dose combinations were tested using three materials: PEGDA, GelMA and HDDA. For each combination, triplicate (nâ=â3) structures with dimensions of 5âÃâ5âÃâ15âmm3 were printed, with successful outcomes being defined by the presence of a sharply delineated structure and a smooth surface finish. Structures that did not meet these requirements, either because they were only partially resolved or because no structure had been produced, were removed from the parameter map. Generally, the print-speed parameter space was not only constrained by the optical dosage but also by the rate at which new material can âwetâ the interface. Inadequate wetting typically caused the interface to fluidically âpinâ to the underlying structure as the polymerization rate exceeded the mass transport of new material.
Microscopy
Micro computed tomography
Micro computed tomography images were acquired using a Phoenix Nanotom M scanner (Waygate Technologies, voxel size of 10âµm3, 90âkV tube voltage, 200âµA tube current and 8âmin scan time). For hydrogel samples, the structures were briefly dried with tissue paper and mounted into a Falcon tube for imaging. For hard materials such as HDDA, the structures were placed on a plastic cap to provide good contrast between the printed structure and the supporting medium. An STL surface mesh was extracted and imported into Keyshot 11 (Keyshot, Luxion) to render the final micro computed tomography representation.
Fluorescence microscopy
Fluorescence microscopy images were captured using a Zeiss Axio Observer Z1 (Zeiss) using either a Ã4 or a Ã10 objective. For constructs that were larger than the objectiveâs field of view, the images were stitched within the Zeiss Zen software to create a large-format image. Once the fluorescence images were acquired, cell-counting was performed on each live/dead image pair using a custom MATLAB script.
Scanning electron microscopy
Scanning electron microscope images were acquired on a FlexSEM 1000 (Hitachi High Technologies). Printed structures on glass slides were mounted directly on the microscope stage with no further sample preparation. The samples did not have a conductive coating applied. The electron microscope was operated in variable-pressure mode at 50âPa. Images were acquired with a 15âkeV beam using the ultra-variable detector. To cover the field of view needed for the large structures, the working distance was typically 40â50âmm, and several images were collected in a tiled manner and stitched together in postprocessing.
Helium-ion microscopy images
Helium-ion microscopy images were acquired with a Zeiss NanoFab using a helium source. During imaging, the flood gun was used to actively neutralize the surface, thus removing the need for a conductive coating. All structures were imaged using an accelerating voltage of 30âkV, a beam current of between 1 and 2âpA, and a field of view of 1,100âµm. Structures were printed directly onto a silanized glass slide and were mounted on the stage using the integrated mounting clips. To facilitate the capture of structures larger than the field of view, several images were taken and later stitched using ImageJ/Fiji.