Dopaminergic action prediction errors serve as a value-free teaching signal

Animals

Male and female adult mice, aged between 2 and 7 months old, from the following mouse lines were used: C57BL/6 J wild-type (Charles River), Drd1-Cre (Gensat: EY262), Adora2a-cre (Gensat: KG139), Slc6a3-cre (JAX: 006660), Ai14 (tdTomato, JAX: 007914), Ai35 (Arch-GFP, JAX: 012735) and Ai32 (channelrhodopsin-2/EYFP, JAX: 024109).

Mice were housed in HVC cages with free access to chow and water on a 12 h:12 h inverted light:dark cycle and tested during the dark phase. The ambient temperature of the rooms was kept between 20–24 °C and the humidity was maintained between 45–65%. Mice used in the COT task were water deprived. Mice had access to water during each training session, and otherwise 1 ml water per mouse was administered. Water was supplemented as needed if the weight of the mouse was below 85%. All experiments were performed in accordance with the UK Home Office regulations Animal (Scientific Procedures) Act 1986 and the Animal Welfare and Ethical Review Body (AWERB). Mice in test and control groups were littermates and randomly selected.

Surgical procedures

Viruses

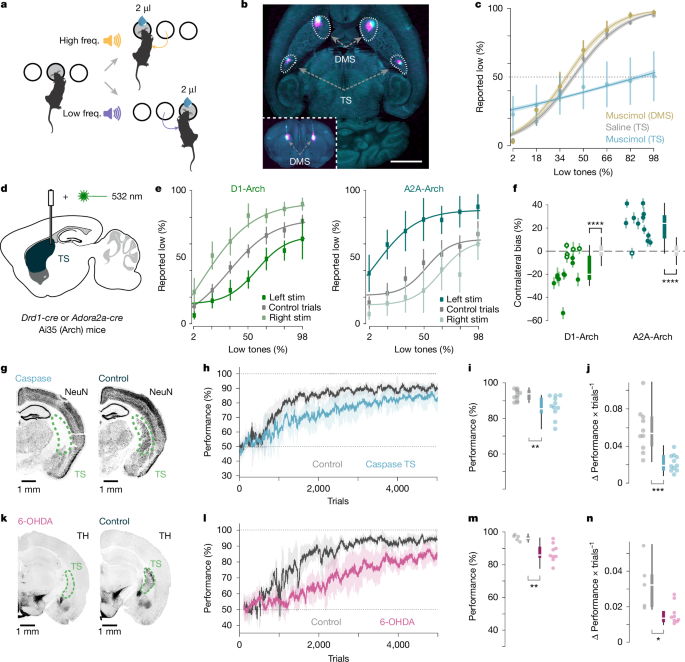
All viruses were made in house except for pAAV5-CAG-dLight1.1 (Addgene, 111067), which was used for the photometry recordings. dLight1.1 expression was induced by injecting 30–100 nl of pAAV5-CAG-dLight1.1 in the TS and 90 nl in the VS. Chronic lesions of the TS were achieved by injecting a 1:1 mix of AAV2/1-hSyn-Cre at 10¹⁴ viral genomes (vg) per ml and AAV2/5-EF1a-DIO-taCasp3-T2A-TEVp at 10¹⁴ vg ml⁻¹. The mix was diluted five times in saline buffer prior to injection. The same surgical procedure, using the virus AAV2/5-CAG-EGFP (3 × 10¹² vg ml⁻¹), was used for the control group. For all chronic lesion experiments, 4 injections (30 nl each) were made in each hemisphere at 4 or 5 different depths to distribute the viruses as evenly as possible and to provide enough coverage.

Viral injection and implant surgeries

Mice were anaesthetized with isoflurane (0.5–2.5% in oxygen, 1 l/min), also used to maintain anaesthesia. Carpofen (5 mg kg⁻¹) was administered subcutaneously before the procedure. Craniotomies were made using a 1-mm dental drill (Meisinger, HP310104001001004). Coordinates are measured from the extrapolated intersection of the straight segments of the coronal sutures between the parietal and the frontal bones. This point usually lies slightly frontal to bregma and is more stereotypic than bregma itself with respect to the brain. The following coordinates were used: TS: 1.8 posterior, 3.45–3.55 lateral, 3.4–3.5 depth; VS: 1.0-1.1 anterior, 1.65 lateral, 4.4–4.5 depth; DMS: 0.5 posterior, 1.45 lateral, −2.0 depth. Viral injections were delivered using pulled glass pipettes (Drummond, 3.5 inch) in an injection system coupled to a hydraulic micromanipulator (Drummond, Nanoject III) on a stereotaxic frame (Leica, Angle Two), at approximately 10 nl min⁻¹. For optogenetic experiments, we used flat optical fibres of 200 μm diameter (Newdoon: FOC-C-200-1.25-0.37-7) and tapered optical fibres (Optogenix, Lambda Fiber Stubs) of 200 μm diameter with 1.5 mm active length, 4 mm implant length. For photometry experiments, flat fibres (Doric Lenses 0.57NA, 200 or 400 μm diameter, 4 to 7 mm long) were implanted vertically, 0.1 to 0.15 mm dorsal of the injection site of dLight1.1. Eight mice that were targeted for TS recordings were not used in any experiments as initial investigation revealed they had reward responses which have not been observed in the TS^44,45. To confirm these fibres were outside the TS in six out of eight of these mice we performed serial two-photon microscopy and confirmed that in all cases the fibres were located outside of the TS. For chronic d-AP5 cannulation experiments, we used 26-gauge guide cannulas (Plastics One, C200GS-5), that were cut to 5 mm below the pedestal. We implanted the guide cannulas in the TS (coordinates: 1.82 posterior, 3.55 lateral, 3.0 depth) and then fit them with a dummy cannula with no projection (Plastics One, C200DCS). All implants were affixed using light-cured dental cement (3 m Espe Relyx U200), which was also used to attach a headbar. In mice that received only injections the wound was either sutured (6-0, Vicryl Rapide) or glued (Vetbond). For photometry experiments a subset of mice had fibres implanted in both the TS and the VS to compare how the signals in these regions developed throughout learning.

Pharmacological manipulations

For muscimol injections, bilateral cranial openings were performed over the DMS and the TS, and a headbar was positioned stereotactically. A landmark that aligned to bregma allowed for future injections in stereotactic positions. Closures of cranial openings were prevented by covering the exposed brain with Duragel (Cambridge Neurotech). Skull was covered with Kwiksil (World Precision Instruments), which was removed before every injection. Before each training session, mice were head-fixed while awake and 30 nl of either muscimol (Sigma-Aldrich) at 0.2 mg ml⁻¹ or saline were injected for experimental and control sessions, respectively, co-injected with cholera toxin B (Cambridge bioscience) of different colours to trace injection sites during histology. After a 15-min period, mice started the training session.

For chronic d-AP5 infusion experiments, we head-fixed the mice for 6 min and then habituated them in the training boxes for the first two days using the protocol described above. Starting from day 3, we administered either saline or 20 mM d-AP5 (Tocris, 0106) bilaterally in the TS using internal cannulas (Plastics One, C200IS) with 0.6 mm projection using a custom-built set up. The mice were awake and head-fixed during the infusion and received an infusion of 500 nl of 20 mM d-AP5 per hemisphere in 3 min, which was followed by a 3 min wait time before internal cannulas were retracted to be replaced by dummy cannulas again. The mice were then immediately put in the behavioural boxes to train in the auditory protocol. After the mice completed ≥3,000 trials, we administered saline in both groups in the following session. For acute d-AP5 infusion experiments, we let these mice train without infusion till they reached expert-level performance. We then infused either saline and d-AP5 in different sessions using the same method described above and measured their performance in the perceptual auditory two-alternative forced choice task.

For dopamine neuron ablations we followed the protocol in ref. ⁴⁴. In brief, we first injected intraperitoneally (10 mg kg⁻¹), a solution made of 28.5 mg desipramine (Sigma-Aldrich, D3900-1G), 6.2 mg pargyline (Sigma-Aldrich, P8013-500MG), 10 ml water and NaOH to pH 7.4. Subsequently, mice underwent surgery, and a solution of 10 mg ml⁻¹ 6-hydroxydopamine (6-OHDA; Sigma-Aldrich, H116-5MG), dissolved in saline buffer was injected. Once prepared, we kept the solution on ice covered from light and injected it within 3 h. If the solution turned brown, it was discarded. For controls we only injected saline buffer. For all manipulation experiments cage mates were assigned to either control or manipulation groups prior to surgery, this was not done through an explicit randomization procedure. Power calculations were not used to define the size of the groups prior to experiments. Experimenters were not blinded to whether mice were in the control or manipulation groups.

Transcardial perfusions

Mice received a lethal intraperitoneal injection of pentobarbital (0.1 ml per 10 g) inducing unconsciousness and death. Once unresponsive, mice were first perfused with phosphate-buffered saline (PBS) followed by 4% paraformaldehyde (PFA). The mice were decapitated, and the brains were extracted and fixed in 4% PFA for 24 to 48 h at 4 °C. Subsequently, brains were stored in PBS until further processing.

Behavioural procedures

Training box

Mouse training was carried out in a sound-isolated box containing the behavioural chamber, which consists of a closed arena of 19 cm × 15 cm with 3 ports located in a wall (1.95 cm from the floor, each port 3 cm from the next). To better separate cues and actions and to increase variability in movement times, the three ports were spaced further apart for photometry experiments. The centre port was located in the middle of one of the long sides of the arena and the choice ports were located in the centre of the shorter sides. The ports are equipped with LEDs so they can be illuminated, and photovoltaic infrared sensors to detect poke events. Water can be delivered through each of the side ports. Ports were purchased from Sanworks or constructed in house to the same standards. Controlling chips were purchased from Sanworks. The chamber was illuminated exclusively with infrared light. Mice were monitored through standard webcams without the infrared filter. Sounds were delivered through one central speaker (DigiKey: HPD-40N16PET00-32-ND) and amplifiers (DigiKey: 668-1621-ND). Bpod (Sanworks) was used to control the state machine, and the software was run using Matlab.

COT task

The COT task is a self-initiated two-alternative-choice paradigm. For behavioural experiments the possibility to start a new trial is signalled by turning on the centre port LED. This LED cue was not present for mice that were used for photometry. Mice start a trial by poking in the centre port and holding their position for 100 to 300 ms. The centre port LED is turned off after that required time has elapsed. In between 0 and 50 ms after poking in the centre port, sound is triggered, lasting for 500 ms. Following poking out from the centre port, mice were trained to poke in either of the two side ports. Two microlitres of water was delivered in only one of the two ports, contingent on the stimulus.

Training procedure

Depending on the training stage, pokes in the wrong port abort the trial. During the first day of training, mice were habituated to the box and the poking sequence by doing a visual version of the task in which both side ports delivered water in every trial. Water amounts were decreased from 5 μl to 2 μl during the first 3 days of training. All photometry recordings started after the initial habituation day and after the reward amount was decreased, but before the performance of the mice improved beyond chance.

For the simple version of the task (not the psychometric), we included an anti-bias protocol to force the mouse to sample from the two ports. The protocol samples every ten trials for the proportion of error trials and calculates the percentages of port choices on those trials, adjusting the target port on the next ten trials to overcome any potential bias, proportionally to the errors and the bias. Therefore, this protocol engages progressively more as the mouse becomes more biased and disengages if the mouse becomes unbiased. This protocol was only active during the initial phases of learning as it uses the proportion of error trials for engagement and calibration. All the experiments using the psychometric version of the task were performed once mice were experts (>85% performance on the simple task). The simple version of the task delivered only the easiest possible trial types, with 98% of tones being from one of the two octaves. For the psychometric experiments, seven equally spaced ratios of high or low tones were used. From the beginning of training, the trial types were randomly interleaved, affected by the anti-bias protocol described above.

Variations of COT task in photometry experiments

Several variations of the COT task were used during photometry recordings. In the outcome value change experiment, unexpected large rewards (6 μl) and omissions were introduced randomly on both sides with a probability of 0.1 each. Mice experience multiple sessions of this protocol to get enough trials of each type.

In the predicted value change experiment, the value of one port was changed 100 trials into a session. This port delivered 6 μl rather than 2 μl, whilst the other port still delivered 2 μl. Mice did multiple sessions of this protocol and experienced both sides becoming the large reward size.

The state change experiment was performed only once per mouse. 150 trials into a training session, the sound that had previously corresponded to the contralateral choice to the recording fibre was changed for a white noise stimulus. This new white noise stimulus overlapped with the original COT frequencies. This white noise was louder than the background white noise and was clearly detectable. The mice were required to make a contralateral response to the white noise to receive a reward.

To test whether the dopamine signals were dependent on an auditory stimulus being present, the sound indicating contralateral turns was omitted in expert mice (silence trials).

In the sound-on-return task, the sound indicating a contralateral turn was played during the return from either side port instead of at the centre port. The sound lasted until the mouse returned and poked into the centre port or at most for 2.5 s. If the mouse did not return to the centre port within 5 s, the subsequent trial would be a classic COT task trial with the sound being played upon poke in into the centre port.

The response to passive sounds was always tested at the end of a classic COT or a sound on return session. Mice were left inside the training box for an additional 10 min while all three ports were covered with custom made lids. During that time both high and low frequency sounds or white noise lasting 500 ms were presented at random time intervals (mean interval 5 s) and in a random sequence.

Sound stimuli

Sounds consist of a stream of 30 ms pure tones presented at 100 Hz (each tone was introduced 10 ms after the previous one). One of two octaves (5 to 10 kHz, or 20–40 kHz) was selected as the target octave to indicate the side port where water was available on that trial. Each 30 ms tone was randomly drawn from 16 logarithmically spaced frequencies on each octave. The difficulty of the trial was controlled by varying the proportion of 30 ms tones from each octave. For example, in a trial catalogued as 82% of high tones, for each 30 ms tone there are 82% chances of playing a tone from the 20–40 kHz octave, and 18% (100% − 82%) chances of playing a tone from the 5–10 kHz octave. These probabilities are independently computed, so two tones from different octaves can sound simultaneously. The overall amplitude of the sound is randomly selected between 60 and 80 dB. The amplitude of the sound during the passive exposure experiments was also 60–80 dB and the sound duration was 0.5 s.

Water delivery

Water was delivered into the two side ports for correct choices using a solenoid valve that was carefully calibrated. As previous studies have suggested that the neurons in the TS are responsive to valve click noises⁴⁵, for the photometry experiments we placed valves outside the training boxes and muffled them using sound insulation foam. In addition, we played quiet white noise constantly inside the training box. We confirmed with a microphone that the valve clicks could not be detected with these precautions.

Photometry and video acquisition in the COT task

Fluorophores were stimulated using 465 nm and 405 nm LEDs (Thorlabs) of max power 0.2 mW. The 465 nm and 405 nm LED amplitudes were modulated using a sinusoid of 211 and 531 Hz respectively. The 405 nm light falls at the isosbestic point for fluorophores of the type used in this study⁶⁰. This enabled separation of signal from movement artefacts and bleaching as done by ref. ⁶¹. Light was passed from the LED source through optical fibres with NA 0.57, through a commutator (Doric Lenses, FRJ 1 × 1 PT 0.15) to a patch cord (Doric Lenses, FC-ZF1.25 LAF). A mini cube and photodetector (Doric Lenses) were used to collect the signal. The signal was then passed to a NIDAQ (National Instruments) and recorded and analysed using custom Python scripts as described in ‘Statistical analysis’. Behaviour was controlled with a Bpod which sent TTL pulses to the NIDAQ at the start of each trial.

Mice were filmed from above during training and recording sessions using a Basler acA640-750um USB 3.0 camera. Videos were acquired at 30 Hz and synchronized with the photometry acquisition using the NIDAQ. For ease of analysis, mice were always trained in the same box and cameras were never moved.

Open-field stimulations

For this experiment we used a 40 cm × 40 cm square arena, and experiments were conducted with ambient light. Sessions lasted for 30 min. See ‘Optogenetic manipulations’ for specifics about the triggered stimulations.

Open-field photometry recordings

For this experiment we used a 50 cm × 20 cm × 28 cm (L × W × H) arena. Mice were allowed to explore the setup for 20 min, during which video footage and photometry recordings were acquired.

Optogenetic manipulations

For opto-inhibition of either the D1 or the D2 SPNs, in 15–25% of trials, randomly selected, a sustained pulse of green (532 nm) light was delivered after mice initiated the trial, always preceding the onset of sound delivery by at least 50 ms and lasting longer than the sound duration. Light intensity was calibrated to 12 mW at the fibre tip.

For dopamine opto-excitation, during the COT task, the first 150 trials of each session were done without stimulation to get a baseline behaviour, and subsequently, stimulated trials were introduced with these parameters: blue (473 nm) light delivered starting at the time of poking and lasting 150 ms in 5 ms pulses at 33 Hz of 4 or 8 mW intensity measured at the fibre tip. For the state–action experiment, stimulation was delivered unilaterally in the centre port for trials in which the state predicted a movement contralateral to the stimulated hemisphere. For the state–outcome experiment, stimulation was delivered bilaterally on one of the two side ports (for the whole duration of the session) every time the mice chose that port (correct and incorrect trials), coupled with water during correct trials. No anti-bias protocol was employed during these experiments. To test for effects on movement initiation, we performed an experiment similar to the one in ref. ⁹. We placed mice in an open field where mice received a blue (473 nm) light stimulation (5 ms pulses at 33 Hz during 500 ms of 4 or 8 mW intensity measured at the fibre tip) if they were immobile for at least one second. For each of these events, there was a 50% chance of triggering the laser. Trials in which light was not delivered were used as within-animal control.

Threat experiments

All mice used in the threat experiment were individually housed in the three to four weeks preceding the experiment⁶². Mice were placed in an arena (50 cm × 20 cm × 28 cm, L × W × H) with a white opaque floor allowing reliable tracking of the dark coated mice. At one end, the arena contained a rectangular shelter (10 cm × 20 cm) made of red Perspex. The other end of the arena constituted the threat zone (20 cm × 20 cm), in which visual stimuli were presented on a computer monitor (51 cm × 33 cm) that was centred above the arena at a height of 30 cm. IR LEDs provided diffuse illumination of the arena. Mice were allowed to explore the entire arena including the shelter for at least 7 min before any looming stimuli were triggered upon their next entry into the threat zone. Visual stimuli were generated using PsychToolBox and MATLAB. A single looming stimulus consisted of five high contrast expanding spots, which expanded linearly from 3°–50° over 0.2 s (235° s⁻¹) and remained at maximum radius for 0.25 s. The inter-spot-interval was 0.4 s. Each mouse was presented with three looming stimuli in one session. All looming stimuli trials were manually triggered for these mice. Minimum inter-trial interval was 90 s.

Photometry and video acquisition in the threat experiment

Data acquisition was controlled using custom scripts in MATLAB or Python and a NIDAQ (National Instruments). Fluorophores were stimulated as described above. Videos were acquired at 30 frames per second using an IR sensitive camera (Basler acA460-750 um USB 3.0) positioned 70 cm away from the arena and 70 cm above its floor. Frame acquisition was triggered using a NIDAQ generated TTL that was also recorded and used for post-hoc synchronization. Real-time stimulus presentation onsets were determined post-hoc using a photodiode (Thorlabs APD430C) and the TTL trigger acquired at 10 kHz.

Imaging

Whole-brain imaging

We imaged the fixed brains using serial section⁶³ two-photon⁶⁴ microscopy. Our microscope was controlled by ScanImage Basic (Vidrio Technologies) using BakingTray, a custom software wrapper for setting up the imaging parameters (https://github.com/SainsburyWellcomeCentre/BakingTray, https://doi.org/10.5281/zenodo.3631609). Images were assembled using StitchIt (https://github.com/SainsburyWellcomeCentre/StitchIt, https://zenodo.org/badge/latestdoi/57851444). The 3D coordinates of the injections and fibre placements were determined by aligning the brains to the Allen Reference Atlas–Mouse Brain (available from https://atlas.brain-map.org) using brainreg⁶⁵ and visualized using custom functions and brainrender⁶⁶.

Immunohistochemistry

Brain slices were all stained following the same procedure: Blocking was performed in staining solution (PBS + 1% BSA + 0.5% Triton X-100) for 15 min. Primary antibodies (1:1,000 in staining solution) were incubated for 2–4 h at room temperature or overnight at 4 °C with rocking. Washes were performed for 15 min with a staining solution. Secondary antibodies (1:500 in staining solution) and DAPI were incubated for 2 h at room temperature while rocking. Slices were then washed in PBS and mounted using Mount Medium. Primary antibodies used were NeuN (abcam, ab104225), tyrosine hydroxylase (TH) (Sigma-Aldrich, AB152) and GFP (Aves labs, GFP-1020) (to reveal dLight-expressing cells). Secondary antibodies used were Alexa-488 anti-mouse (Invitrogen, AB_2534069), Alexa-567 anti-chicken (Invitrogen, AB_2535858), and Alexa-647 anti-rabbit (Invitrogen, AB_2535813).

Quantification of chronic lesions

Brains were sliced using a cryotome at a thickness of 30 μm. Fifteen to 20 slices covering the entire striatum at regular intervals were selected for NeuN staining. Slices were mounted in standard glass slides using standard mounting medium and subsequently imaged in the Slide Scanner (Zeiss) using a 20× objective. Individual slices were registered to the Allen Reference Atlas–Mouse Brain (https://atlas.brain-map.org) using ABBA (https://github.com/BIOP/ijp-imagetoatlas), and the NeuN channel was thresholded automatically, per slice, based on the intensity levels in the cortex. The coverage of NeuN staining in the striatum was determined for each slice, and the inverse was determined as lesioned area.

Quantification of dopamine neuron ablation

Brains were sectioned and mounted as described for the chronic lesions but stained for TH to specifically label dopamine cell processes. Slices were imaged using the Axio Scan (Zeiss). Manual regions of interest were drawn for the striatum, the cortex, and the background in each slice. For each slice, the mean intensity in the striatum was normalized to the cortex following background subtraction, and the relative intensity between the striatum and cortex was calculated. For the analysis of the correlation with the performance, data was normalized within each mouse (posterior striatum ratio/anterior striatum ratio). One mouse was removed from the analysis owing to lack of ablation (except in Extended Data Fig. 3j).

Statistical analysis

Behavioural data pre-processing for learning rate experiments

Sessions with less than 60 trials were omitted, the first 5 trials of each session were discarded, and trials in which the mouse was not engaged (defined as having an inter-trial interval longer than 3 times the median value of that session) were not considered for analysis. Together, this amounts to less than 2% of data discarded. The remainder of the trials were ordered chronologically. Mice that did not learn the task (end performance less than 55%) were discarded from the analysis. This amounts to a total of three mice in the whole study.

Psychometric fitting

The LogisticRegressionCV from scikit-learn package in Python was used to fit the data from the psychometric version of the task. This was only used for visualization purposes.

Learning rate experiments

The first 5,000 trials for each mouse were used for analysis. To calculate individual learning parameters, per mouse, we modelled the performance of every mouse using a modified Weibull function^67,68: \({\rm{performance}}=50+a(1-{2}^{{(\frac{-{\rm{trials}}}{l})}^{s}})\). The maximum performance was defined as the maximum of the median of the trials, binned using a window of size 200. Parameters were fitted using the scipy package in Python (optimize.minimize function). Statistical differences between the groups for these parameters were calculated using the non-parametric test Kruskal–Wallis from scipy.stats.kruskal. Significance of the behavioural correlation with the lesion size was performed using the scipy.stats.linregress function. To calculate the differences in performance at different times in learning, we first removed those trials in which mice were extremely biased towards one of the two ports. Bias was determined as described in ‘Behavioural procedures’, and extremely biased trials were defined as those having a value larger than twice the standard deviation for the whole dataset. This correction was not applied to calculate the significance of the observed differences. Two mice (one experimental and one control) were removed for the chronic lesions experiment as they did not learn the task at all, and we suspected that they were deaf. Additionally, the two last sessions of one control and one experimental mouse were removed as the performance dropped to chance. One experimental mouse was excluded from the dopamine cell ablation experiment as the lesion quantification showed no ablation (this mouse performance was comparable to controls). At each point in training, performance was defined as the performance of the past 100 trials. To assess the significance of the differences between the two groups, the data were binned using a window of 100 trials, and the differences between the means of each group were calculated. To generate a shuffled dataset, experimental labels (for example, lesion or control) were randomly assigned to each mouse, always maintaining the proportion of labels on the original dataset, and differences between groups were calculated the same way. We did this 10,000 times. The same procedure was used to analyse the data from the dual-controller model comparisons. The global significance of the dataset was assessed as the likelihood of the cohorts being different at any time, in comparison to the shuffled groups. Mixed ANOVA was used from the pingouin package.

Opto-inhibition experiments

Each individual session contains a few hundred trials, seven trial types, and between 15 and 25% of stimulated trials. A session of 300 trials can have as few as 6 (300 × 1/7 × 0.15) stimulated trials for a particular type. This can generate a large variability when calculating the proportion of binary choices, as each individual trial will have a large influence (17% in our example). To assess the significance of the biases caused by the optogenetic manipulations, we generated, for every session, a baseline distribution (1,000 shuffles) of port choice proportions for every unstimulated trial type (proportion of high versus low tones), using the same number of trials that were stimulated for that trial type. This generated the natural variability in the potential choices for each trial type and was used to assess the significance of the biases for individual sessions. The total bias for each session was defined as the average difference between opto-stimulated and unstimulated trials for all trial types. Only sessions with more than 150 trials in total were selected for analysis. For mice in which more than data for more than one session and stimulation type was available, we selected the one with the best performance, which is a good indicator of how well a mouse was doing on the task and we reasoned would offer the most stable control to compare the effect of the stimulation to. This resulted in only 3 sessions removed from the dataset, from a total of 30. Including all sessions or changing the session selection method did not alter the significance of the results. The statistical significance for each group was calculated using the non-parametric test Kruskal–Wallis from scipy.stats.kruskal, comparing the observed biased values of every session against a randomly-sampled counterpart, per session, using the variance described above. Only sessions in which the mice did the psychometric version of the task were included in this analysis.

Dopamine photometry pre-processing

The raw data were demodulated offline using custom Python scripts to produce traces that corresponded to the signal (465 nm) and background (405 nm) channels⁶¹. Then the data were processed according to the methods described in ref. ⁶⁹. In brief, the demodulated traces were denoised using a median filter and a low-pass Butterworth filter (10 Hz cut off). The resulting signal and background channel traces were high-pass filtered at 0.001 Hz to correct for photo-bleaching. To correct for motion artefacts, the background channel data were fitted to the signal channel data using a linear regression. The proportion of signal that was explained by the background channel was then subtracted from the signal channel component, such that only the signal specific to the 465 nm excitation frequency remained. Finally, dF/F was calculated by dividing this signal by the baseline fluorescence (the signal channel trace filtered using a low-pass filter with a cut off at 0.001 Hz). All traces were z-scored to allow better comparison across mice and sessions.

Peak dopamine responses were calculated using the Python package PeakUtils or by taking the maximum value of the trace if no peak was found in a given window. For cue responses, the window was between the cue onset and entry into the choice port. For action (APE) responses, the window was between the time of exiting the centre port and entry into the choice port. For outcome responses (used in the outcome value manipulation experiment) the window was between the time entry into the choice port and 200 ms later. As VS dopamine clearly dips to omitted rewards, instead of calculating peaks, the mean of the dopamine response within this window was used as an estimate of the response.

Kernel regression model of photometry signal

Following ref. ¹², we built a linear regression model to predict the photometry signal at each time point from the behavioural events around this time. In this model, the predicted dLight response is calculated as the convolution of a time series a,b, etc., representing different behavioural events as series of 0 s and 1 s, where 1 s represent the occurrence of the behavioural event. This means that at time t, the predicted dLight response g(t) is given by the weighted sum of the different behavioural events shifted in time within a set window. The model can be expressed as follows:

where \([{\tau }_{x}^{-},{\tau }_{x}^{+}]\) gives the shifted time window in which behavioural event x is allowed to influence the predicted photometry signal. k^a, k^b, etc. are the kernels for the behavioural events, or equivalently, the linear regression weights for the events at each different time shift. When plotted as a time series, these regression weights form the estimated response profile for the dLight signal due to a given behavioural event. These regression coefficients were estimated using the linear regression function of the Python package scikit-learn.

Behavioural events were selected from trials in which the mouse did not repeat events (for example, did not repeatedly poke their head in the centre port). The model was fitted for each mouse for each session as the signal in the TS and VS evolved over learning. As the choice movement initiation time is unclear and may start prior to the withdrawal of the head from the centre port is detected, the movement kernels were allowed to extend 0.5 s prior to the event. As the movement duration was longer than the cue and outcome responses, the movement kernel was allowed to extend 1.5 s after the event, whereas the cue and outcome kernel windows were limited to 1 s after the event.

Calculation of explained variance by behavioural variable in kernel regression model

The calculation of the percentage variance explained by the full model was performed per session per mouse and then averaged across sessions. To calculate the percentage variance explained by each regressor, the predicted dLight signal was recalculated without that particular regressor, inspired by ref. ⁷⁰. The explained variance of the new prediction compared to the true signal was then calculated. Finally, the percentage variance explained by the removed regressor was calculated by comparing the explained variance of the full model, v_full, to the explained variance when that regressor is removed from the prediction calculation v_partial, using the following equation:

Although this method does give a decent comparative measure of the contribution of each regressor to the explained variance of the data by the prediction, it can result in percentages larger than 100 if the predicted dLight signal without that regressor performs worse than the intercept at explaining the data. This can be seen for some of the VS recordings without the outcome regressor.

In Fig. 2g the full photometry trace was used to estimate the percentage variance explained, both for the full model and the individual regressors. This includes extended periods with no behavioural events as the task is self-paced. This may lead to an underestimate of the percentage of the photometry signal that is explained by the task. To account for this the percentage variance explained was recalculated solely on the portions of the photometry trace for which there were behavioural events, a process we refer to as ‘trimming’. This trimming was only done in Extended Data Fig. 4m.

Additionally, we explored including return to centre movements as behavioural events for the kernel regression model. These events were taken from the time of the mouse leaving the choice port and taking a ‘direct’ route back to the centre port. To assess how direct the path taken by the mouse to the centre port was, we used the tracking data (see below) and computed the cosine similarity between the optimal path from the side port to the centre and the path taken by the mouse. Return vectors with a cosine similarity ≥0.9 to the optimal vector (within the first 10 s of leaving the choice port, or when the mouse entered the centre port) were included in Extended Data Fig. 4j,k and were considered for inclusion in the regression. Return event kernels had a window from 0.2 s prior to and 1.5 s after leaving the side port. This was chosen to be conservative so as to avoid crossover with the next trial/prior choice movement and to be comparable to choice movements within the task, which had a mean duration of 0.68 ± 0.53 s (ipsi) and 0.68 ± −0.61 s (contra), for which the kernel window also extended 1.5 s after leaving the port.

For ease of visualization and alignment, only short return movements (≤1 s) were included for the averages in Extended Data Fig. 4j,k.

Regression predicting current trial dopamine from past choices

We performed a linear regression (using statsmodels.api.OLS) predicting the size of the dopamine response (TS dopamine at time of choice, VS dopamine at time of cue) on correct contralateral trials from previous choices for the same stimulus. We included data from throughout training for this analysis. A positive regression coefficient means there is a larger dopamine signal on the current trial when the side chosen on the current trial was chosen in response to the same stimulus in the past (how far in the past is given by the x axis). A negative regression coefficient means that the dopamine response is smaller when the chosen side had been chosen in response to the same stimulus in the past. Separate regressions were performed for each ‘lag’ (number of trials back value).

Video tracking during photometry recordings and quantification of movement parameters

The position of the mouse was tracked using DeepLabCut⁷¹ and variables such as speed, acceleration, angular velocity and angular acceleration were calculated using custom scripts in Python. As the videos for the freely moving experiment were taken at a slight angle, the coordinates were transformed into standard space using custom Python scripts. Videos taken during the COT task were taken from above so there was no need for such a transform. Speed and acceleration were calculated using the nose as a marker. For angular velocity and acceleration, a triangle was formed using the nose and the two ears and a line was drawn from nose to the line between the two ear markers. This line from the nose to the back of the head was taken as the heading direction of the mouse. Turn angles were calculated using the cumulative angular velocity. In the task, 0° was defined as the angle when the mouse leaves the centre port. To calculate the maximum turn angle in the task, a sigmoid curve was fitted to the cumulative angular velocity for each trial between the sound onset and entering the choice port. The upper plateau of the sigmoid (maximum fitted cumulative angular velocity) was then taken to be the turn angle for the trial.

To determine the coarse relationship between the turn angle and the size of the dopamine response, trials were divided into four quantiles based on the size of the dopamine response between the mouse leaving the centre port and entering the choice port for contralateral choices. Turn angles were divided into using the quantiles that were created from the size of the dopamine response. A regression slope was fitted (using the function stats.linregress from the Python package SciPy) between the average quantile turn angle and average quantile dopamine response for each mouse for each session. The fit slope was then compared to the fit slope if the x and y quantile labels were shuffled in. The data were shuffled 100 times and the distribution of the fit slopes from the actual data were compared to the shuffled distribution.

In the freely moving experiment, turns were defined as the moment when the angular velocity crossed a threshold of ±0.5 s.d. Turns were required to last at least 0.06 s and were only included for analysis if no other turns occurred in the preceding or subsequent 0.5 s. The head angle at the times of turn onset was then used to define 0° turn angle and turn angles were determined using the cumulative angular velocity from this time point.

Regression of speed, turn angle and trial number

To investigate whether changes in turn angle and speed could account for the decrease in TS dopamine response size with trial number seen in Fig. 3, for each mouse we built a linear regression model predicting dopamine response size for all trials from speed and turn angle. The resulting predicted signal was subtracted from the actual signal per trial, before regressing the residuals against log trial number. To calculate the relative contributions of speed, turn angle and trial number, we also built a regression model with all three predictors to estimate the respective variance explained.

Dopamine opto-stimulation experiments

To quantify the bias for each session, we calculated the choice differences between the first 150 trials (pre-stimulation), and the subsequent trials, as long as there were more than 100 trials. Sessions in which the initial bias of the mouse to either of the ports was larger than 2:1 were removed from the analysis. We averaged the biases if several sessions existed for the same mouse on the same stimulation conditions, so that we had only one observation per condition. We used the non-parametric two-sided Wilcoxon sign-rank statistic (scipy.stats.wilcoxon) to calculate the significance of the observed biases.

For the open-field stimulation, we calculated the speed of the mouse as the difference between the position of the mouse in each frame, convolved with a kernel of size 5 for smoothing purposes. The overall threshold to consider that the mouse was moving was determined empirically, but the results presented were invariant across a large range of values tested. Instant speed was calculated as the average speed from movement initiation to 300 ms after. Average movement was calculated from stimulation to 5 s later. We used the t-test on two related samples (as above) to assess the significance of every parameter.

Analysis of the effect of a large dopamine response on subsequent trial bias

Data analysis was inspired by ref. ⁷². Dopamine responses considered in this analysis were reward responses for the VS and movement-aligned responses for the TS. Dopamine responses were categorized as large or small based on whether they were larger than or smaller than the 65th percentile respectively. The average change in percentage of contralateral choices was calculated for large and small dopamine responses on the preceding trial for each level of sensory uncertainty on the current trial (which correspond to the different percentage mixtures of tone clouds described in ‘Behavioural procedures’). A logistic regression was performed (using statsmodels.api.Logit) to investigate the relationship between dopamine response size on the previous trial, perceptual uncertainty and the choice (repeat or switch) on the current trial.

For this analysis, we used data from the psychometric version of the task. Mice were required to meet certain behavioural criteria in order for their data to be included: the slope of the psychometric curve at the Point of Subjective Equality to measure sensitivity and bias at the edges (the ‘easy’ trials). Bias was calculated by taking the difference in percentage correct at the two easy trial types. Mice were required to have a slope ≥1 and a bias ≤0.09 to be included, acting as a measure how well the mice had learned the task. This ensured that all mice in the analysis had similar behaviour, with little bias and strong discrimination between stimuli.

For this analysis, following Lak et al.⁷², only trials where mice made a correct choice were included. Note that, as the tail dopamine response is taken between movement onset and reward delivery, for the ambiguous trials (50% high and low) the mouse would have no information as to the outcome of their choice at this time point. Therefore, all trials of this type were included.

For the VS mice, the dopamine reward responses were used so only correct trials could be used. For the TS, correct trials were used for all stimuli other than the ambiguous stimulus. For the ambiguous stimulus, both correct and incorrect trials were used. The TS dopamine responses are taken aligned to movement, prior to reward being delivered.

Regression predicting movement similarity based on TS dopamine size

We performed a linear regression (using statsmodels.api.OLS) between the current trial TS dopamine response at time of choice and the Fréchet distance⁷³ between trajectories on the current and subsequent trial (which provides a measure of the similarities between the two trajectories that takes into account the location and ordering of the points along a curve, with a low value indicating high similarity between the two trajectories). Fréchet distances were computed recursively.

Opto-inhibition during learning

For the experiment in which opto-inhibition was done at different points in learning, mice only did the simplest version of the task (stimuli were either 98% of high tones or 98% of low tones). The initial 20 trials of every session were discarded, and the baseline distributions of choice proportions and the session bias were calculated as indicated above. Because mice performed close to perfection in this version of the task, we only included in the analysis the choices to the port where biases were expected to happen, in agreement with our previous results (it is not possible to measure any positive contralateral bias in a trial in which the mouse chooses the contralateral port all the time in unstimulated trials). Mice were all implanted bilaterally, and the stimulated implant was alternated every day of training. We only included in the analysis those implant sites which resulted in at least one significantly biased session (P < 0.05, calculated as indicated above). This removed 4 implants from the analysis out of 17. The regression models were done for each individual implant, and the average slope for each genotype was calculated. The significance of the global results were assessed against random datasets, generated by shuffles of the performance values associated with every session. P values were calculated as the proportion of ‘random slopes’ being larger (expecting negative and positive contralateral biases for D1-Arch and A2A-Arch, respectively).

Computational modelling

Modelling of APE and RPE photometry signal

The RL model used an actor–critic framework with soft-max (inverse temperature = 5.0) policy selection. The model used a semi-Markov state representation, previously introduced by⁷⁴ to capture the time-course variability of dopamine commonly seen in experimental tasks. In the semi-Markov formalism, the agent keeps track of its current state as well as a representation of ‘dwell time’ within that state. Actor, critic and stimulus–action strengths are then updated only when a state transition takes place. It has the added advantage that the states in the model directly correspond to the within-trial behavioural stages of the task, while allowing for representation of time. This formalism has been previously used in prior work modelling dopamine signals in tasks with variable timing^75,76 and it allows us to model the time course of dopamine in a more realistic manner than other previous studies, which have often assumed that each time point within a behavioural stage of the task is an independent state (see ref. ⁷⁷ for a review).

The states consisted of Start, High tone, Low tone, Outcome, as well as an action state associated with each of the time of action for each sound and action pairing (in order to align to the time of action to match the data). Actions consisted of Left, Right, Centre and Idle to represent the movement to enter left, right and centre ports (and not taking an action). A state transition happened when the agent moved between one of the above states, for example the start state to the high tone state. The behaviour is self-paced for the mice, with sometimes multiple seconds of variability in timing between trials. The critic had dimension 1 × n states. The actor had dimension n states × n actions. The non-value dependent model had dimensions n states × n actions.

The RPE was scaled according to dwell time in the state to approximate temporal discounting⁷⁴ as is necessary for the semi-Markov representation. RPE was calculated at each state transition k as

where \({r}_{k+1}\) is the reward received in the new state, \({\rho }_{k}\) is the average reward per time step and \({d}_{k}\) is the time spent in the last state before transitioning. \({\rho }_{k}\) was calculated by looking at average reward per time step in the last n (n = 500 in our model) state transitions:

The critic value function was then updated using the RPE \({\delta }_{k}\) signal:

and the actor stimulus–action value function was updated in a similar manner:

where α and β are both learning rates that were set to 0.005.

As in ref. ⁷⁴, the RPE signal was then taken to be \(\sigma ({\delta }_{k}+\psi )\), where \(\sigma (x)=0\) if \(x\le 0\) and \(\sigma (x)=x\) if \(x > 0\). \(\psi \) was set to be 0.2 to represent a baseline level of dopamine.

The non-value dependent model calculated APE, \({\delta }_{{a}_{k}}\), at state transitions (see Extended Data Fig. 6b to see full set of actions and states in the modelled task) as the difference between the action taken, a_k, and the stimulus action strengths given the stimulus \(A(s)\), according to the equation

APEs were rectified, resulting in only one component of the APE vector being non-zero, essentially providing a scalar update signal. This rectification also matched the data better as dips in TS dopamine were never observed at time of action. Importantly, this rectification did not change the general properties of the algorithm. Stimulus–action pairing strengths were then updated using APE:

where ε is the rate at which the stimulus–action association was formed, which was set to 0.01 for all simulations apart from the predicted value change experiment simulation, where it was set to 0.001 to mimic how a value-free controller should update slowly. For other simulations this was less relevant as we aimed to show the direction of change of APE and RPE signals rather than their relative rates of updating (Extended Data Fig. 8).

Every time the mouse revisited a state it had visited before, a counter \(I(s)\) was increased to keep track of how many times that state had been visited:

This was used to compute novelty N, which decayed exponentially with exposure to a state, according to

Salience L was computed as a weighted combination of value and novelty of the state:

In the above equations, \(\gamma \) and \(\mu \) were set to 0.01 and 0.5, respectively.

In all simulations except for the simulation of the effect of previous choice on subsequent dopamine response (Fig. 3i,l), the inverse temperature term of the soft-max was set to 5.0. For Fig. 3i,l it was set to 0.5, to better capture the more exploratory nature of the behaviour of the mouse and to ensure there were enough trials throughout learning with both ipsi- and contralateral previous choices.

The movement model of dopamine comprised a vector with length equal to the number of actions available. When an action was taken, the corresponding element in the vector was set to 1. All other elements were 0.

In all candidate models of dopamine photometry signals, learning rates and constants were not fitted to match the numbers of trials taken to learn the task seen in the experimental data, so trends should be interpreted as approximations of general patterns rather than models of the exact behaviour.

Dual-controller network model

We simulated a task with two states (the first element, s = 1, corresponds to low tone, the second element, s = 2, corresponds to high tone) and two actions (first element corresponding to right and the second corresponding to left, a = 1 or a = 2). We modelled two parallel systems, one for the value-based controller that is updated by RPE, this had two components, an actor and a critic. The second system had a value-free controller that was updated by APE. The actor in the value-based controller and the value-free controller were modelled as a weight matrix (dimension 2 × 2) that projected from the sensory states to the two possible actions that could be taken, the weights within these matrices are notated as \({W}_{{\rm{actor}}}\) and \({W}_{{\rm{tail}}}\). The critic in the value-based controller was modelled as a 2 × 1 matrix, \({W}_{{\rm{critic}}}\), with each sensory state projecting to one of the cells in the matrix. The output for the \({W}_{{\rm{actor}}}\) and the \({W}_{{\rm{tail}}}\) on each trial was computed as the weight matrix × the state input—that is, \({A(s)}_{{\rm{actor}}}={W}_{{\rm{actor}}}s\) and \({A(s)}_{{\rm{tail}}}={W}_{{\rm{tail}}}\,s\).

To calculate the actual action taken by the model, we first calculate the action predicted by the sum of the outputs of the two controllers. An additional noise term was added, \({A(s)}_{{\rm{noise}}}\) (drawn from a uniform distribution between 0 and 1):

The action associated with the maximal value of \({A(s)}_{{\rm{total}}}\) was the action a that the model took (corresponding to the choice of the mouse)—that is, \(a={\rm{argmax}}({A(s)}_{{\rm{total}}})\).

The model received a reward, r = 1, if the index of the action taken, a, corresponded to the action rewarded (here r = 1 if: s = 1 and a = 1 or s = 2 and a = 2).

We then computed the RPE and APE signals. For the RPE signal, we first calculated the predicted value from the critic as \(V={W}_{{\rm{critic}}}\,s\). We then calculated the reward prediction error as

To calculate APE and represent it as a scalar value we first binarized the instantaneous predicted action vector: \({A}_{{\rm{tail}}}^{{\rm{binary}}}\), such that the index corresponding to the maximum \({A}_{{\rm{tail}}}\) was 1 and 0 everywhere else. Then we computed the predicted action \({p}_{a}\) (initialized at 0) as a low-pass filter of this binary choice vector:

with a time constant \({\tau }_{{\rm{tail}}}=100\). The APE was then calculated as \({\delta }_{{\rm{APE}}}=a-{p}_{a}\) for the action taken.

Finally, we updated the \({W}_{{\rm{actor}}}\) and \({W}_{{\rm{tail}}}\) weights as a function of a three-factor learning rule that included the sensory state, the action taken (that is, both the value-based actor and the value-free controllers receive an efference copy of the action taken) and the APE/RPE signal on the current trial:

where β = 0.02 is a learning rate;

where α = 0.04 is a learning rate.

The \({W}_{{\rm{critic}}}\) weights were updated by a two-factor learning rule that included the sensory state and the RPE signal on the current trial:

The RPE weights of the actor also decayed to its steady-state value of 1 with a time constant of \({\tau }_{{\rm{decay}}}=100\):

The \({W}_{{\rm{tail}}}\) and \({W}_{{\rm{actor}}}\) weights were bounded to be positive and were initialized to 1. The \({W}_{{\rm{critic}}}\) values were initialized as 0 and were also bounded to be positive.

We simulated 100 trials. A trial lasted 1,000 timesteps (2,000 for the inactivations). For plotting the performance, we low-pass filtered the reward with a time constant of 10 a.u., starting from 0.5. The inactivations were conducted at time 30, 100 and 1,000 after which either the \({W}_{{\rm{actor}}}\) (for the RPE system) or the \({W}_{{\rm{tail}}}\) (for the APE system) were set to 0 and weights were not plastic anymore. For the psychometric curve, we varied the difficulty level d from 0 to 1 and set the first element of \(s=1-d\) and the second element of \(s=d\). For the TS dopamine stimulation simulations, we doubled the APE signal.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.