DNA-guided transcription factor interactions extend human gene regulatory code

Clones and protein expression and purification

Cloning, protein expression and purification were performed essentially as described previously⁹. Most coding sequences for the expression constructs encoded⁹ extended DNA-binding domains (eDBDs) that enriched expected motifs in a previous study⁵¹ (Supplementary Table 1). New eDBD constructs were designed as described previously⁹ and synthesized by GenScript. Gateway recipient vectors for protein expression were constructed using pETG20A modified to include an N-terminal 6×His tag⁵¹ (prey construct), or pDEST15 (Invitrogen, 11802014) modified to include a C-terminal streptavidin-binding peptide (SBP; bait construct). The prey constructs were from a previous study⁵¹, bait constructs were generated by Gateway cloning to the modified pDEST15 bait vector and the activities of the produced proteins were evaluated using HT-SELEX. In total, 158 SBP-tagged bait and 419 His-tagged prey TF proteins were expressed in E. coli.

The proteins were expressed using the auto-induction protocol as described previously⁹. In brief, the Rosetta 2(DE3) pLysS strain of E. coli (Millipore, 71403) and Invitrogen BL21-AI Competent E. coli (Thermo Fisher Scientific, C607003) were used for the expression of eDBDs that were inserted into pETG20A-6×His and pDEST15-SBP vectors, respectively. Transformed cells were first cultured at 37 °C in 500 µl TB medium in the wells of a 96-deep-well plate overnight, and then transferred into auto-induction medium (1:40 dilution) supplemented with either 0.05% glucose and 0.2% lactose (Rosetta 2(DE3) pLysS E. coli) or 0.05% glucose and 0.02% arabinose (BL21-AI E. coli). The cells were then cultured at 37 °C for 4–6 h, followed by 30 h at 16 °C. The cells were collected by centrifugation and resuspended in either buffer A (300 mM NaCl and 10 mM imidazole in Tris-Cl, pH 7.5; Rosetta 2(DE3) pLysS E. coli) or PBS (BL21-AI E. coli). Both buffer A and PBS were supplemented with 0.5 mg ml⁻¹ lysozyme and 1 mM PMSF. The cells were then subjected to two freeze–thaw cycles to ensure lysis, followed by addition of DNase I and MgSO₄ to 10 µg ml⁻¹ and 1 mM final concentrations, respectively, to digest the released DNA. The Rosetta 2(DE3) pLysS E. coli lysates were incubated with Ni-Sepharose 6 Fast Flow resin (Cytiva, 17-5268-01), and the BL21-AI E. coli lysates with glutathione sepharose 4B (Cytiva, 17-0756-01) for 1 h with 1,200 rpm shaking, after which the lysates were transferred into individual wells of a 96-well filter plate (Nunc, 278011). Ni-Sepharose beads were washed three times each with 600 µl buffer A with 10 mM and 50 mM imidazole, and glutathione sepharose beads with 600 µl PBS. The bound proteins were eluted from beads by using either buffer A containing 300 mM imidazole or fresh 10 mM glutathione buffer in Tris-Cl, pH 8.0. The activities of the eluted proteins were examined using HT-SELEX, and the E. coli clones, in which active proteins were obtained, were used for larger-scale protein expression in 100 ml of auto-induction medium to obtain enough proteins for CAP-SELEX screening (using a similar protocol but with proportionally larger lysis and wash volumes). The concentration of the individual proteins obtained in a scaled-up culture was measured using spectrophotometry at 280 nm, and the proteins were diluted to 50 ng ml⁻¹ when possible, supplemented with glycerol to 50% final concentration, and stored at −20 °C.

HT-SELEX, CAP-SELEX and mixture-SELEX

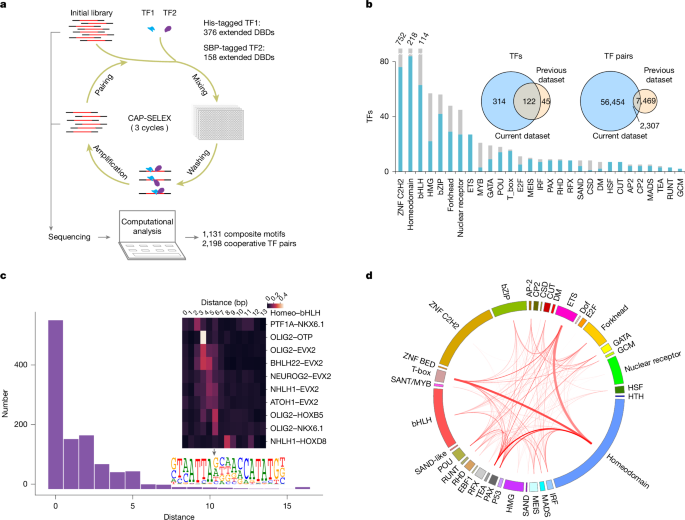
HT-SELEX and CAP-SELEX were performed as described previously⁹, with some improvements. The Flag tag was replaced with a His tag to make affinity purification more efficient and less costly, and the data analysis pipeline was automated (see following paragraphs). The SELEX ligands were similar to those used in a previous study⁵¹; they contain 40-bp random sequences and Illumina sequencing adaptor sequences on both sides, and were designed for characterizing the cooperativities of the TF pairs. The single-stranded oligonucleotides containing the ligand sequences were purchased from Eurofins Genomics (Supplementary Table 1) and the double-stranded selection ligands were obtained by performing one-step PCR with primers binding to the adapters⁵². In CAP-SELEX, 158 prey proteins were screened against a set of 376 bait proteins arranged on 384-well plates. During the screen, some bait proteins were replaced on the 384-well plate, resulting in analysis of a total of 58,754 interactions. All tested TF–TF pairs are listed in Supplementary Table 2. For CAP-SELEX, around 1 µg dsDNA ligands was mixed with around 100 ng purified His- and SBP-tagged proteins in 50 µl Promega buffer (4% glycerol, 1 mM DTT, 500 µM EDTA and 50 mM NaCl in 10 mM Tris-Cl, pH 7.5) in individual wells of 96-well MultiScreen MSDV 0.65-µm hydrophobic filter plates (Millipore, MSDVN6510). For a given plate, each sample well contained the bait protein for the plate, and a well-specific prey protein; each plate also contained eight control wells of known interacting pairs (from ref. ⁹; the bait–prey pairs used were CEBPD–ATF4, CEBPD–ETV5, FOXO1–ETV5, TEAD4–CLOCK, FOXO1–GCM1, HES7–TFAP2C, TEAD4–ONECUT2 and HES7–ETV5). After incubating for 30 min at room temperature, 1.2 µl Ni-Sepharose beads (GE, now Cytiva, 17-5268-01) were added and the incubation continued for 2 h on a Timix microplate shaker with a speed of 1,300 rpm. The beads were then washed three times with a microplate washer (405 LRS, BioTek), and the protein–DNA complexes were eluted from the beads using 60 µl Promega buffer with 300 mM imidazole. The eluted complexes were transferred into Echo Qualified 384-Well Polypropylene Microplates, in which each well contained 1.25 µl His Mag Sepharose Ni Beads (Cytiva, 28967390) pre-blocked by 0.5% BSA and 0.1% Tween 20. After incubation for 30 min on a VWR DMS 2500 Microplate shaker with a speed of 1,900 rpm, the beads were washed seven times with a Tecan Hydrospeed 384-well microplate washer and the bead suspension was used for PCR as previously described⁹. The selection process was repeated three times and the PCR amplicons from the third cycle as well as the initial library were sequenced using Illumina HiSeq 2000 with 50-bp single-end reads. The screen revealed 2,198 TF–TF interactions and the preference of the proteins from one TF family to interact with proteins from other TF families was calculated and visualized using circos v.0.69-8 (Fig. 1d).

Mixture-SELEX was used to test whether the composite motifs could also be recovered by simply mixing the two TFs and performing SELEX (Extended Data Fig. 2c–g). It was performed as described previously⁵³. The protein expression was performed as described above, except the bacterial cells were incubated for 8 h at 37 °C until a density suitable for induction was achieved, followed by incubation for 40 h at 17 °C. Only one overnight freeze–thaw cycle was used for lysis. The lysis buffer contained 400 mM NaCl, 100 mM KCl, 10% glycerol, 0.5% Triton X-100 and 10 mM imidazole in 50 mM potassium phosphate buffer, pH 7.8; the concentration of MgSO₄ during incubation with Ni-Sepharose beads was 15 mM. The concentration of imidazole for protein elution from beads was 500 mM, and Bradford reagent (B6916, Sigma) was used for estimating protein concentration. For mixture-SELEX, two TF proteins (200–600 ng) were added to individual wells of a 384-well plate containing the DNA ligands (in the first cycle approximately 1.5 µg of annealed and elongated oligonucleotides; in subsequent cycles 200–500 ng of PCR product from the previous cycle) in a final volume of 20 µl. The final composition of the binding buffer was 125 mM NaCl, 1.1 mM MgCl₂, 0.7 mM dithiothreitol, 0.07 mM EGTA, 17.8% glycerol, 3.7 μg ml⁻¹ poly-dI-dC and 1.4 µM ZnSO₄ in 22 mM Tris-Cl, pH 7.5. The proteins were incubated with the DNA ligands at room temperature for 20 min. Then, 1.75 µl of magnetic Ni-Sepharose beads (GE Healthcare) were washed in Promega (50 mM NaCl, 1 mM MgCl₂ and 4% glycerol in 10 mM Tris, pH 7.5) + 0.2% BSA, stored in the same solution with the addition of 0.01% NaN₃ and 0.1% Tween and diluted in 25 μl of SELEX buffer (100 µM EGTA, 1 mM dithiothreitol, 5.37 µg ml⁻¹ poly-dI-dC and 1.9 µM ZnSO₄ in Promega buffer, pH 7.5) right before adding to every well with SELEX reaction. The mixtures were then further incubated for 20 min at room temperature, aspirated and washed with cycles of volumes (1 × 300 µl, 6 × 50 µl, 3 × 100 µl, 6 × 50 µl, 3 × 100 µl) low-salt wash buffer (5 mM EDTA and 1 mM dithiothreitol in 5 mM Tris-Cl, pH 7.5). The elution of ligands was performed by adding 35 µl of elution buffer (1 mM MgCl₂ and 0.1% Tween in 10 mM Tris, pH 7.8) followed by incubation at 80 °C for 10 min. Eluted ligands were amplified by PCR (Phusion DNA polymerase) and used as input ligands for the next SELEX cycle. Three SELEX cycles were performed. The selected ligands from the third cycle were sequenced (Illumina HiSeq 2000) and compared with existing input library sequences (from PRJEB20112).

Discovery of spacing and orientation preferences

To detect the spacing preferences of DNA-bound TF–TF pairs, we compared data from the HT-SELEX and CAP-SELEX using a novel algorithm based on mutual information (MI) (https://github.com/YinLabTJ/MI_CAP-SELEX). The underlying rationale is that if two TFs cooperatively bind to DNA with a preferred spacing, the 4-mers at the positions with the preferred spacing will enrich together, which results in an increase of MI between the two positions.

First, for each individual TF, we identified the local maxima 8-mers (8-mers that were more enriched than any other sequence within one Huddinge distance⁵⁴) from cycle-3 or cycle-4 HT-SELEX data that were enriched more than fivefold compared with input (cycle 0) sequences (Supplementary Table 4). We then partitioned each 8-mer as well as its reverse-complementary sequence into a set of ten 4-mers (Extended Data Fig. 1b), which were indexed as follows: 1 to 5 in the forward orientation, followed by the reverse complement 4-mers indexed 6 to 10 starting from 6 being the reverse complement of 4-mer number 5. This resulted in the identification of one or more sets of 4-mers for each TF, representing each locally maximal 8-mer.

For each CAP-SELEX TF pair, we then analysed the spacing between each pair of 4-mer sets between the two TFs. To detect all four possible orientations between the 8-mers, we paired the 4-mers of the two 4-mer sets in two ways: (1) forward orientation, in which a 4-mer with index number j in a set is paired with the 4-mer in the other set that has the same index number; and (2) inverse orientation, in which j is paired with 5 + j when j = <5 or j − 5 when j > 5. The 4-mers that were present in both sets were excluded from the analysis to exclude signal from individual TF-binding sites. The spacing preferences were then evaluated by converting the counts of the 4-mers to probabilities (the number of reads with an expected 4-mer in a specific position was divided by the total number of reads), followed by MI analysis of the 20 4-mer pairs at all CAP-SELEX read positions at which the positions of the 4-mers do not overlap (equation (1)).

where P(4-mer + 4-mer) is the observed probability of a 4-mer pair in position 1 and position 2; P_pos1(4-mer) and P_pos2(4-mer) are the marginal probabilities of individual 4-mers in position 1 and position 2, respectively; and MI represents the sum of mutual information of all 20 pairs of 4-mers; for each TF pair, MI was calculated separately for each possible pair of enriched 8-mers (4-mer sets) of the individual TFs.

The 4-mers were used for the analysis because shorter k-mers are too frequently present in both sets, and longer k-mers are not present frequently enough to remove sampling noise, which will contribute to MI.

The MI heat map in Extended Data Fig. 1b shows the MI for all possible two positions of the 4-mers on the CAP-SELEX ligands. To automatically identify the TF pairs that cooperatively bind to DNA with a preferred spacing, a set of 380 TF–TF pairs was manually curated to detect spacing preferences, and this set was then used as a ground truth for setting a threshold for the automatic analysis based on analysis of receiver operating characteristic (ROC) curves (Extended Data Fig. 9c). We first ranked the MI values for each 4-mer pair, and selected the top 5% (representing 28 of 561 position pairs). If there is no cooperative binding, these would be distributed randomly, and represent multiple possible spacings and orientations. However, we found that in the interacting pairs, the top 5% MI signals were concentrated to fewer than 6 spacings and orientations. This analysis generally identified strong spacing preferences, but was not able to detect weak spacing preferences, or most cases in which the TF pair bound to composite sites, where the motif differed from the binding motifs of the individual TFs.

Detection of composite motifs

To detect composite motifs, we developed an algorithm (https://github.com/YinLabTJ/Relative_Affinity_CAP-SELEX) to compare the relative affinities of 10-mers in CAP-SELEX versus the individual HT-SELEX to identify 10-mers that are strongly enriched in CAP-SELEX but not in the individual TF HT-SELEX.

To derive relative affinities from counts, we used the following process. The model is based on the assumption that SELEX is a thermodynamic affinity-based selection process, with the following set of coupled equilibria for the DNA molecules in the pool:

Here D_i is the i-th species of molecules in the DNA pool, T the TF or TF pairs, and T:D_i the TF–DNA complex. If F denotes the fraction of D_i in the pool and K_d(D_i) the dissociation constant for the i-th equilibrium, the relationship between post-selection frequencies F′ and the preselection frequencies F can be shown as in ref. ⁵⁵:

After multiple rounds of selection, most of the TF or TF pair is assumed to bind to the optimal DNA sequence and the relative affinity K_a of DNA sequence D_i in terms of the frequencies in cycle r and cycle 0 can be expressed as:

Approximation is based on a previous study⁵⁵. F_ref indicates the frequency of the most abundant sequence in the pool. We next adapted the above equation to infer a table of relative affinities K_a(k) for all k-mers k with a length l, based on an assumption that a single k-mer on the DNA ligand dominates the rate at which the DNA ligand is selected. Then the relative affinity of a specific k-mer k can be estimated as:

P₀(k) denotes the expected frequency of k in the initial DNA pool and is computed using a fifth-order Markov model (Extended Data Fig. 9d).

The relative affinities for individual 10-mers were calculated in the DNA libraries enriched from cycle 3 of CAP-SELEX and from that of the two corresponding HT-SELEX experiments. The data were then plotted in an xy plot, in which the y axis is the relative affinity in CAP-SELEX and the x axis is the higher of the relative affinities in HT-SELEX (https://github.com/YinLabTJ/Relative_Affinity_CAP-SELEX). If the relative affinity of a 10-mer was ranked at the top 50% and 1.5 times higher in the CAP-SELEX library than in the corresponding HT-SELEX library, the 10-mer with the highest relative affinity within a Hamming distance of 1 was used as an initial seed to generate a composite motif. Note that for a given pair, multiple seeds could be generated this way.

Generation of PWMs and motif logos

Position weight matrices (PWMs) were generated using Autoseed⁵⁴. Autoseed⁵⁴ generates motifs using a multinomial model (figure 1b in ref. ⁵⁶) that describe the enrichment of small set of sequences close to a highly enriched k-mer or set of k-mers described by an IUPAC degeneracy code (figure supplement 1 in ref. ⁵⁴; open source code to identify local maxima and generate motifs are available in https://github.com/jutaipal/kmercount_with_localmax; https://github.com/jutaipal/multinomial_motif_generator; motifs can also be generated with the Moder package⁵⁷ https://github.com/jttoivon/moder2). Of note, the resulting models are not optimized to describe the entire sequence population enriched in CAP-SELEX, as this would generate a mixture of the dimeric and monomeric motifs. The motifs are based on the multinomial model, using background corrected counts⁵². If a seed is used to select sequences to be included in the motifs on the basis of a simple alignment using Hamming distance (for example, a Hamming distance of 1), there will be heavy bias towards the consensus sequence, and a motif resembling the seed will be recovered even from random sequences. This is because if a consensus base is present at position i of a seed k-mer, 3 (k − 1) sequences where another position is not consensus are included in the motif (because they are one substitution away from the seed, at a Hamming distance of 1). However, if a non-consensus base is present at i, sequences with other substitutions will not be allowed, because they are a Hamming distance of 2 away from the seed, owing to two substitutions, one at site i and another at the other position (left side of figure 1b in ref. ⁵⁶). To eliminate this bias, we use a multinomial method⁵². In brief, to estimate mononucleotide distribution at position i, we identify the counts of the (degenerate) consensus sequence and three (classes of) other sequences that contain base substitutions at position i. After background correction⁵², the counts of these four (classes of) k-mers are used to generate the PWM at position i (see right side of figure 1b in ref. ⁵⁶). Because the base whose mononucleotide distribution is interrogated does not contribute to the alignment, the seed alignment bias is eliminated. Note that because the multinomial method derives the distribution of mononucleotides at each position from different sequence populations, the nucleotide counts at each position do not add up to the same value (unlike in the case in which unseeded alignment is used to identify sequences to be included in a motif).

Autoseed was used with the following modifications. The third cycle of CAP-SELEX was used for PWM generation. The number of seeds for each TF pair was determined on the basis of k-mer local maxima⁵⁴, and the motifs were classified as primary, secondary, tertiary and so on, on the basis of the number of matches to the seed. Autoseed-generated seed was used at first, and was refined on the basis of the PWM generated as described previously⁵⁶ with minor modifications. The length of seed was defined by extending to flanking positions when the ratio between the most and the least frequent bases at the flanking position was greater than 2. Where indicated (Supplementary Table 3), to increase the number of reads included in the model, the seed was made more redundant to accommodate more sequences at positions at which the frequency of the most common base was less than 0.5. At these positions, N was used, except where the ratio between the second and the third most frequent bases was greater than 2, in which case the IUPAC symbol for the two or three most frequent bases was used. Furthermore, if the length of the seed was greater than 10 bp, where indicated, a multinomial model (multinomial = 2) allowing a single mismatch at any position (in addition to the position whose mononucleotide distribution was measured; see figure 1b of ref. ⁵⁶) was used. As described previously⁵⁶, seed sequences were further manually curated to prevent the mixing of two distinct binding modes, and to distinguish between monomer and dimer models. The final seed and PWM were checked for internal consistency. Count motifs are provided in Supplementary Table 3. All motifs are also available through the CIS-BP database (https://cisbp.ccbr.utoronto.ca/). A subset of motifs that are distinct from each other is also available in HOCOMOCO (https://hocomoco11.autosome.org/).

SELEX motif collection

Because the automated composite and spacing pipelines also discover some motifs of the other type, we classified each motif as either composite (motifs overlap or specificity changes) or spacing (TF–TF motifs that contain the two individual motifs but exhibit a specific spacing and/or orientation preference) as follows: all TF–TF pair motif and the individual motif logos were inspected separately by four experts (J.T., Y.Y., Y.C. and I.S.), and classified to the composite, spacing or unclear class. Discordant calls were then resolved at a meeting. The collection of new motifs contains 1,131 composite motifs, 205 spacing motifs and 12 HT-SELEX motifs. The motif collection was augmented with 2,585 previously published SELEX motifs for human and mouse TFs. A set of 133 mouse and 687 human HT-SELEX motifs was obtained from a previous study⁵⁶, excluding low count and replicate motifs. A set of 31 human HT-SELEX and 562 CAP-SELEX motifs were obtained from a previous study⁹ by excluding technical replicates and ChIP-exo motifs. An E2F8 motif was obtained from another study⁵³, and ten human motifs were obtained from another study⁵⁴. A set of 864 HT-SELEX and 297 Methyl-SELEX motifs were obtained from a previous study⁵¹. The set of Methyl-SELEX motifs included only the MethylPlus, Multiple effects and Inconclusive motif categories. In total, the collection contains 3,933 motifs. The protein families of TFs were extracted from ref. ³, from the original publications or from UniProt. The position count matrices and associated metadata of the 1,348 new motifs are provided in Supplementary Table 3.

Dominating set analysis

To identify a smaller set of distinct motifs, commonly referred to as representative motifs, we performed a network analysis called the minimum dominating set in a similar manner to what was described previously^9,51,56. This analysis identifies a minimum number of motifs in such a way that for every motif in the full set, there will be a representative motif that is similar to it. First, the similarities were computed between all motif pairs using SSTAT (Motif statistic software suite v.1.1)⁵⁸. A network of motifs was constructed so that two motifs (nodes) were connected by an edge if the SSTAT Ssum similarity score was greater than 1.5 × 10⁻⁵. Then, the minimum dominating set of the network was found so that every node not belonging to the dominating set was connected to at least one node in the dominating set; the minimum dominating set is the smallest of such sets. The problem is solved as an integer linear programming problem. The SSTAT Ssum similarity score was obtained with the following options: 50% GC content, pseudocount regularization and 0.01 type I threshold. The dominating set analysis of the collection of 3,933 motifs resulted in 1,232 representative motifs with distinct sequence specificities. Of the new motifs, 347 composite motifs and 112 spacing motifs were representatives (Supplementary Table 3). The dominating set analysis was also performed for the new 1,131 composite motifs alone, resulting in 391 distinct composite motifs. The motif similarity of zinc finger TFs was calculated and visualized using motifStack v.1.38.0 (https://github.com/jianhong/motifStack).

Motif matching and motif enrichment analysis

The 3,933 SELEX motifs were matched to the repeat-masked human genome GRCh38 using MOODS^59,60 with default settings, except that the binding affinity score threshold was set so that approximately 300,000 matches were recovered for each motif. This was done by first setting a low threshold (2, natural logarithm), and then selecting a score threshold that resulted in the recovery of at least 300,000 matches. For some motifs, fewer than 300,000 matches had a score of 2 or more.

For analysing motif match enrichment at cell-type-specific candidate cis-regulatory elements (cCREs), the cCREs of 111 human adult cell types were derived from the cis-element atlas (CATlas⁴⁴). The cCREs were identified as non-coding open chromatin regions from single-cell ATAC-seq data on 30 adult tissues. The authors of the CATlas study⁴⁴ identified around 400,000 cell-type specific cCREs at which the ATAC-seq signal showed cell-type-restricted patterns, and divided them into distinct cCRE sets specific to 15 cell-type groups.

To investigate whether the motif matches are enriched or depleted at the cell-type-specific cCREs, we applied Fisher’s exact test (one-sided) similarly to the previous study⁴⁴. We computed the P value to evaluate the deviation from the null hypothesis that the presence of a motif match at a cCRE is independent of whether the cCRE belongs to a set of cell-type-specific cCREs.

The number of cell-type-specific cCREs that have a motif match is a random variable X and follows a hypergeometric distribution

where k is the observed value of X, m is the number of all cCREs with a motif match, n is the number of cell-type-specific cCREs and N is the number of all cCREs. The motif match enrichment at particular cell-type-specific cCREs was determined as relative enrichment compared with the frequency of matches of the same motif at all cell-type-specific cCREs, defined as relative frequency fold change \(\textlog_2\left(\frack/nm/N\right)\). The P value for the enrichment or depletion was computed as follows: if the log₂-transformed fold change was larger (enrichment) or smaller (depletion) than 0, the P value was computed as the upper P(X ≥ k) or lower P(X ≤ k) tail cumulative density of the hypergeometric distribution, respectively. A representative composite or spacing motif was marked as enriched in a cell-type group if for any cell type in the group, the P value was less than 0.01 and the log₂-transformed fold change was greater than 0.75. Using the false discovery rate (FDR; Benjamini–Hochberg method) with a q-value cut-off of 0.01 (calculated either across motifs separately for each cell type or across all motifs in all cell types together) resulted in the same representative composite and spacing motifs enriched in at least one cCRE set, so for clarity we chose to report the uncorrected P values. For a visualization of the enrichment and depletion of a set of representative bHLH–homeodomain spacing motif matches at cell-type-specific cCREs (Fig. 5c), only cell types for which the −log₁₀ P value of the enrichment or depletion was equal to or more than 50 were selected. The −log₁₀ P values were visualized as a heat map created with the ComplexHeatmap Bioconductor package (v.2.16.0, using a custom colour palette shown in the scale)^61,62. In the heat map, red denotes the −log₁₀ P value for the enrichment and blue denotes the log₁₀ P value for the depletion. The statistical analysis and visualization were conducted in R.

For analysing motif enrichment in ChIP–seq peaks, we downloaded all TF ChIP–seq bed files for all cell lines from the ENCODE database (https://www.encodeproject.org/, ref. ¹⁷, downloaded on 6 October 2024) that were labelled ‘Default analysis’, used GRCh38 assembly and did not contain any match to the word ‘treat’ in the description. Experiments were excluded from the analysis if the data contained fewer than 1,000 peaks, or if the P value of the 1,000th peak sorted by ‘signalValue’ was more than 0.01. We then identified regions of overlap for all interacting TF–TF pairs described in this study using bedtools v.2.30.0 (ref. ⁶³), and applied the same peak quality filters to the sets of overlapping peaks. Bed files were then converted to fasta files using bedtools v.2.30.0 (ref. ⁶³). The matching of PFM models to the fasta files was then performed by MOODS⁶⁰, using a default P-value cut-off of 0.0001. The final enrichment was calculated as the sum of MOODS scores divided by the length of the regions in the respective bed files. For statistical testing, the binomtest one-sided function from SciPy library v.1.10.0 was used. For a list of the bed files and motifs used in the analysis, see Supplementary Table 2. For the analysis shown in Fig. 2c, ChIP–seq bed files for FOXK2 (experiment series: ENCSR786QMI, K562 cell) and ELF1 (experiment series: ENCSR918LYT, K562 cell) were downloaded from the ENCODE database and the common peaks in the two replicates of the same TF ChIP–seq experiment were used for downstream analysis as described above. The enrichment score was calculated as the occurrence frequency of the motif in ChIP–seq peaks.

Logistic regression analysis

To study whether the adult human cell-type-specific cCRE elements could be predicted by the linear combinations of the effects of TF motif matches, we built a logistic regression classifier with lasso regularization. The logistic regression model predicts whether a cCRE i is specific to a certain cell type (class 1) or not (0). The model is trained separately for all 111 cell types, the class 1 corresponding to cCREs of a specific cell type and class 0 corresponding to cCREs specific to all other cell types. The class of a cCRE i, i ∈ 1, …, N is a random variable Y_i, which is modelled as generalized Bernoulli regression with the logit link function, also known as the logistic regression

where the probability of class 1 for sample i, π_i depends on d features x_i = [x_i1, …, x_id]^T. The features x_i correspond to the motif matches of d − 1 TFs or TF pairs and the intercept term. The coefficients w describe the feature effects on the class 1 probability π. As features x_i, we adopted either binary presence (1) and absence of the motif match, or the binding affinities of the motif matches (0 if no binding; if multiple matches per cCRE, consider the maximum affinity score). We only considered the matches of the representative motifs (d = 1,232).

We applied a lasso-regularized logistic regression by minimizing the penalized negative log-likelihood

where \(| | w| _1=\sum _j=1^d| w_j| \) is the L1 norm of the vector w and λ is the regularization parameter. To evaluate the model performance and to optimize the value for the regulation parameter λ, a nested cross-validation (CV) was performed. The outer fivefold CV was used to obtain area under receiver operating characteristics curve (AUC) values, and the inner tenfold CV was used to optimize the regularization parameter λ. The lasso-regularized logistic regression was trained using the glmnet R package^61,62.

The means and standard deviations of the AUC values obtained from the fivefold CV for different cell-type-specific models within the cell-type groups are shown in Supplementary Table 4 for both the model with binary features and the model with affinity score features. The predictive performance varied between cell types, with the mean AUC values varying between 0.55 and 0.75. In general, the models with the affinity score features reached a better predictive performance and the further results were produced by this model. The final model was trained with all data, the regularization parameter again optimized with tenfold CV. The cell-type-specific regression coefficients were centred (subtracted by the mean) and scaled (divided by the standard deviation). For two pairs of TF protein families, ETS–RUNT and Forkhead–ETS, the representative motifs were selected. For these motifs, the regression coefficients are visualized as a heat map for those cell types for which the absolute scaled regression coefficient was at least 2 for at least one motif.

Evolutionary conservation analysis

To identify the possible conservation of TF–TF–DNA interactions described by the motifs, we followed a procedure similar to one described previously^9,51. In brief, to test whether the composite and spacing motifs explain the patterns of evolutionary conservation observed in the non-coding genome, we compared the conservation at the motif matches of each TF–TF pair with the conservation at the motif matches of artificial control motifs.

To obtain a set of artificial heterodimeric control motifs that still contain the specificities of the individual TFs, each heterodimeric motif was divided in half using all possible split points so that the lengths of the divisions were at least one-third of the length of the whole motif (rounded down). Then, for each split, three control motifs were formed by concatenating the ‘right’ and ‘left’ halves, the ‘left’ and ‘right’ reverse complement halves and the ‘left’ reverse complement and ‘right’ halves. The artificial control motif generation was also performed for the monomeric motifs in the representative set. To prevent generating artificial control motifs that are similar to the corresponding true motif, the 10-mer gapped similarities (gapped k-mer similarity: https://github.com/jutaipal/motifsimilarity) were computed between the true motif and the artificial control motifs. Control motifs with a similarity larger than 0.1 with the original motif were excluded from the set of control motifs.

We compared the evolutionary conservation of genomic sites recognized by each heterodimeric motif with sites recognized by artificial control motifs. To identify the evolutionary conserved motif matches, we used the conservation scores and constrained nucleotides in the human genome defined by the Zoonomia Consortium^38,64,65. By comparing the genome sequences of 241 placental mammal species, Zoonomia defined the slower than expected (conservation) and faster than expected (acceleration) evolution for every base in the human genome as positive and negative P values, respectively, also known as phyloP scores⁶⁶. In addition, Zoonomia identified the most significantly (FDR < 0.05) conserved nucleotides in the human genome (phyloP score \(\ge \) 2.27, around 101 Mb or 3.26% of the genome) and called them the human constrained nucleotides.

For a given TF–TF–DNA interaction, we considered the matches of the true motif and the corresponding artificial control motifs that overlap the human constrained nucleotides. The matches overlapping protein-coding exons from GENCODE v.44 or simple tandem repeats from UCSC were removed from the analysis. For the matches of the true motif that overlap the human constrained nucleotides, the average phyloP scores were obtained and a two-component Gaussian mixture model (GMM) was fitted to the scores to separate constrained matches and non-constrained matches⁶⁷. Ten GMMs were randomly initialized and the best model according to the Bayesian information criterion was chosen as the final model. The GMM fitting results in a threshold value for the motif match being constrained; if the average phyloP score of a motif is higher than the threshold value, the probability that the motif belongs to the constrained set is higher than the probability of not belonging to the constrained set. This analysis results in a different threshold for different motifs (Supplementary Table 4).

The matches of both the true motif and the artificial motifs were merged into one list and 10,000 non-overlapping matches with the highest affinity score were selected. The average phyloP scores were obtained at these motif matches, and the matches with an average phyloP score exceeding the motif-specific threshold were defined as conserved.

To study which TF–TF pairs the motif matches are enriched for in human constrained elements, Fisher’s exact test was applied to the contingency table in Extended Data Fig. 8a to obtain the P value for the statistical significance. We computed the number of conserved sites (k) and non-conserved sites (n − k) for the original motif, as well as the number of conserved sites (m − k) and non-conserved sites (N + k − n − m) for the corresponding artificial motifs. The P values were computed only for the enrichment, using the upper tail cumulative density of hypergeometric distribution. The P values were adjusted to control the FWER (the probability of making at least one false positive in the set), using Holm’s method in R. The numbers of evolutionarily conserved matches for true motifs and for artificial control motifs were compared as described previously⁹, and the enrichment was quantified as the conditional frequency fold change \(\frack/n(m-k)/(N-n)\). The fold enrichment values were plotted as the function of the number of conserved motif matches among 10,000 highest-scoring matches (Extended Data Fig. 8). The number of the new conserved composite motifs was defined with an FWER threshold of 0.05. Statistics are provided in Supplementary Table 4.

To study whether the conservation of one half-site of the composite motif increased the probability of the conservation of the other half-site, we computed the correlation of phyloP scores across each base position within the matches of the composite motif that were included in the set of 10,000 true motif and the artificial motif matches (see above). To define an empirical Gaussian null distribution for the phyloP correlations between different base positions, the phyloP correlations were computed also within the matches of the corresponding artificial motifs. The P value for correlations was obtained by calculating the probability, under the null distribution, of observing a correlation at least as high as that which was observed. The P values for each motif were subjected to FDR correction in R (Benjamini–Hochberg). The correlations and the corresponding q-values can be represented as a triangular matrix. The triangular matrix can be divided into two triangles corresponding to the half-sites of the motif and a square corresponding to the correlations between the half-sites. The square was further divided into an upper triangle and a lower triangle. The lowest q-value of the lower triangle was chosen as the statistical significance of the correlation between the half-sites of the composite motif. The conservation of the halves of the composite motif was significantly correlated, with FDR < 0.05.

For the evolutionary conservation analysis of the orientation and spacing preferences of TF–TF pairs, we analysed the 1,291 TF–TF pairs that showed orientation and spacing preferences (Supplementary Table 2) for which the monomeric motifs of both individual TFs are found in the full collection of 3,933 SELEX motifs. Because the IRF8, MAFF, NFATC1, SOX11, TGIF2LX and ONECUT1 motifs are homodimers, their motifs were replaced by artificial half-site motifs. For each TF–TF pair, we chose the first 6-mer count table from Supplementary Table 7, and identified the most preferred orientation and spacing. Then, for each individual TF in the pairs, we chose a monomeric motif. If there were many motifs for the same TF, we first excluded any Methyl-SELEX motifs, and chose the shortest motif. If many motifs were identical in length, we chose the PWM that best matched the representative 6-mer (the 6-mer score was calculated for all positions and orientations within the corresponding PWM, and a maximum was taken, recording the position and orientation of the match so that the 6-mers could be aligned to the PWM matches later). For palindromic 6-mers that had identical scores in both forward and reverse orientations, we recorded the forward orientation. Next, for each monomeric TF motif, and for each set of corresponding artificial control motifs (see above), we identified approximately 300,000 genome-wide matches of the individual TFs. The matches overlapping protein-coding exons (from GENCODE v.44) or simple tandem repeats from UCSC were again removed from the analysis. The monomeric motifs matches that had a gap of fewer than 30 bp in the genome in different orientations and spacings were then identified, and compared with the spacings in the 6-mer tables. The analysis was performed for both the true motif pairs and for motif pairs in which one member is the true motif and the other is one member of the set of the artificial control motifs for that TF. We then extracted the average phyloP scores at the paired monomeric motif matches, and computed for each orientation and spacing the number of match pairs in which both matches are conserved, using the motif-specific thresholds for the average phyloP score (Supplementary Table 4). The number of conserved motif match pairs was then compared with the empirical null distribution derived using the control motif sets. The P value for the conservation for each orientation and spacing is computed as the probability of observing the number of conserved true motif match pairs or a more extreme value given the null distribution. The P values were subjected to FDR correction using the Benjamini–Hochberg method, with an FDR threshold of 0.01. To determine whether the number of conserved orientations and spacings is significantly higher than what is expected by random, a Fisher’s exact test (one-sided) was used.

Relative affinity of individual motifs to composite motifs

To determine how well individual TFs could bind to composite motifs in the absence of their partner, we calculated a score differential. For this, a consensus sequence was derived from both composite motifs and the corresponding individual motifs. Motif matching for individual motifs against the corresponding collected consensus sequence was performed using MOODS with the P value set to 0.0001. The maximum score of the individual motifs against the composite motif consensus sequence and the maximum score of the individual motif against its own consensus sequence were compared and are plotted in Extended Data Fig. 3g.

Difference between the composite motif core and the individual TF motif flanks

To determine how often the part of the composite motif that overlaps with both individual motifs (composite overlap) differs from the individual TF motifs, we aligned the motifs of individual TFs against the composite motifs and quantified the difference between the composite overlap regions using two methods: JSD and the Jaccard index of the highest-affinity k-mers. First, for each individual TF in the composite pairs, we chose a monomeric motif from the collection of 3,933 SELEX motifs (excluding Methyl-SELEX motifs) in which the dimeric motifs for IRF6, MAFF, NFATC1, ONECUT1, SOX11 and TGIF2LX were replaced by the six artificially created monomer motifs. For TFs with multiple monomers in the collection, the shortest motif was chosen; for equal-width motifs, the one with the highest information content was selected. Of the 1,131 composite motifs, 15 do not have monomeric motifs for either one or both individual TFs; these were consequently not analysed. We then aligned the motifs of individual TFs against the composite motifs using TOMTOM⁶⁸, with a significance threshold of one. Only composites for which the flanks of the aligned monomers overlapped were selected for further analysis. In addition, cases in which the overlapping region did not correspond to the monomer flanks were removed from the analysis, resulting in a set of 977 TF1, TF2, composite motif triplets that were analysed further. For each triplet, the sections of the corresponding PWMs that constituted the overlapping region were extracted (composite overlap as PWM_co; TF1 and TF2 overlaps as PWM_TF1o and PWM_TF2o, respectively).

To determine the distance between the overlapping PWMs, we used the JSD metric, which is symmetric and bounded, and enables measurement of the difference between PWMs as bits of information. For JSD analysis, for each base position i in the overlap, we quantified how distinguishable the base distributions are between the overlapping regions of the composite motif and the individual motifs by computing the total JSD as the sum of JSDs of all PWM positions. A high JSD indicates different base distributions between the overlapping parts of the PWMs. Composite PWM_cos having a total JSD of higher than 0.5 bits to either of PWM_TF1o or PWM_TF2o were considered to be distinct.

To determine whether the DNA sequences matching the overlapping regions of the motifs are different, we used the Jaccard index of k-mers. For this analysis, we determined the difference between the composite motif core and individual TF motif flanks on the basis of whether they have high affinity to the same k-mers. The 975 triplets in which the overlap was shorter than 13 bp were analysed. All k-mers of the length of the overlap were scored against PWM_co, PWM_TF1o and PWM_TF2o, and k-mers with at least 90% of the maximum score were selected. Subsequently, we computed the Jaccard index between the composite k-mers and TF1 and TF2 k-mers. Composite cores with a Jaccard index lower than 0.5 against both of the flanks were defined as different from the flanks. The Jaccard indexes and the JSDs for the composite core–flank pairs are shown in Extended Data Fig. 3h,i with examples of individual TF motifs aligned against composites with the overlapping composite cores and flanks highlighted. Extended Data Fig. 3h,i also illustrates the correspondence between the JSD and the Jaccard index for the selected composite motifs.

Protein expression, purification and crystallization

Expression and purification of the DBD fragment of human HOXB13 (residues 209–283), MEIS1 (residues 279–333), TEAD4 (residues 40–112), FOXK1 (residues 302–400), ELF1 (residues 186–305) and BARHL2 (residues 232–292) were performed as described previously^51,69,70. The DNA fragments used in crystallization were obtained as single-strand oligos (Eurofins), and annealed in 20 mM HEPES (pH 7.5) containing 150 mM NaCl and 0.5 mM Tris(2-carboxyethyl)phosphine (TCEP) and 10% glycerol. For each complex, the purified and concentrated protein was first mixed with a solution of annealed DNA duplex at a molar ratio of 1:1.2–1.5 and after one hour on ice was subjected to the crystallization trials.

The crystallization conditions for HOXB13 homodimer and HOXB13–MEIS1 heterodimer complexes were optimized using an in-house-developed crystal screening kit combining different PEGs with different additives. For the first screening of other complexes, we used the screens Nuc-Pro from Jena (Jena Bioscience), ProPlex from Molecular Dimensions (Anatrace Products) and PEGRX and Natrix from Hampton Research (Hampton Research). All crystals were obtained in sitting drops by using the vapour diffusion technique. The HOXB13 homodimer–DNA complex was crystallized from the solution containing 19.6% PEG(3350)MME, 0.15 M KCl and 8% PEG(400) in 50 mM Tris-Cl, pH 8.0. The HOXB13–MEIS1–DNA complex was also crystallized from the solution containing 17.6% PEG(5000)MME, 0.06 M MgCl₂, 0.15 M KCl and 4% pentanol in 50 mM Tris-HCl, pH 8.0. The HOXB13–TEAD4–DNA complex was crystallized from the solution containing 15% PEG(4000), 0.5 M (NH₄)₂SO₄ and 4% PEG(550)MME in 50 mM MOPS, pH 7.24. The FOXK1–ELF1–DNA complex was crystallized from the solution containing 14.4% PEG(3350)MME, 0.1 M MgCl₂ and 8% PEG(200) in 50 mM Na-HEPES, pH 7.2. Crystals of BARHL2 complexes with two different DNAs were obtained in the same conditions from the reservoir solution containing 50 mM sodium cacodylate buffer (pH 6.5), 7–10.5% PEG(4000) and 5% butanol (longer DNA) or PEG(200) (shorter DNA). All datasets were collected at the ESRF from a single crystal on beamline ID23-1, at 100 K using the reservoir solution as cryo-protectant. Data were integrated with the program XDS⁷¹ and scaled with SCALA^72,73. Data collection statistics are presented in Supplementary Table 5.

Structure determination and refinement

All structures were solved by molecular replacement using the program Phaser⁷⁴ as implemented in PHENIX⁷⁵ and CCP4 (ref. ⁷³), with the structure of related proteins obtained from the PDB or from the structure collection of our laboratory: structure of HOXB13–DNA(CAA) (PDB ID 5EEA, chain A) as a search model for HOXB13; structure of MEIS1 (5BNG, chain A) as a model for MEIS1; structure of TEAD4 (5GZB, chain A) as a model for TEAD4; structure of FOXK1A (2C6Y, chain A) as a model for FOXK; and structure of ELF3 (3JTG, chain A) as a model for ELF1. For the two BARHL2 dimers, we used the BARHL2 monomer structure⁷⁶. After the positioning of protein, the DNA sequence was manually built to the density using Coot⁷⁷. The rigid body refinement with REFMAC5 was followed by restrain refinement with REFMAC5, as implemented in CCP4 (ref. ⁷³) and Phenix.refine⁷⁸. The manual rebuilding of the model was done using Coot. The refinement statistics are presented in Supplementary Table 5. Figures showing structural representations were prepared using PyMOL (https://www.pymol.org/pymol.html).

The atomic coordinates and diffraction data for six novel structures presented in this study have been deposited to the PDB with the accession codes 8R7Z and 8R7F for homodimers of BARHL2 bound to different DNAs; 8BZM for the FOXK1–ELF1–DNA structure; 8BYX for HOXB13 homodimer bound to DNA; 5NO6 for the TEAD4–HOXB13–DNA structure; and 5EG0 for the MEIS1–HOXB13–DNA structure.

Computational prediction of structures

The AlphaFold multimer model⁷⁹ was used to predict the structures of cooperative TF pairs that were mediated by protein–protein interaction (MYC–MAX, CEBPD–ATF4 and FOS–JUN), facilitated by DNA (MEIS1–HOXB13 and MEIS1–DLX3) or dependent on DNA (HOXB13–TEAD4) by running the following command:

python3 docker/run_docker.py \
–fasta_paths=multimer.fasta \
–max_template_date=2020-05-14 \
–model_preset=multimer \
–data_dir=$DOWNLOAD_DIR \
–output_dir=$OUTPUT_DIR

The predicted structures were refined and are shown in Fig. 4a. The r.m.s.d. was calculated for each structure and is shown in the figure legend.

The predictions of protein–DNA complexes were performed with RoseTTAFold2NA v.0.2 and AlphaFold 3. For details, see Supplementary Table 6.

DNA sequences extracted from PWM files of TFs showing spacing or orientational preferences were used as input for the program. Using the max_index function for vertical axis on PWM values, the DNA sequence has been reduced to the form kmer1_XN_kmer2, where kmer1 is the most probable k-mer for TF1, kmer2 is for TF2 and XN is spacing preference with X nucleotides between them. The final DNA used for input had the form of either flanks_kmer1_XN_kmer2_flanks_competing_flanks (preferred DNA is on the 5′ side of the top strand), or the reverse case: flanks_competing_flanks_kmer1_XN_kmer2_flanks (preferred DNA is on the 3′ side). In that sequence, flanks were GCGAG and XN was X nucleotides from the cycled GCGA sequence. The competing sequences were for several cases covering all possible orientation preferences and three or four spacing preferences:

orient_1_2: kmer2_XN_kmer1

orient_1_3: revcompl(kmer1)_XN_kmer2

orient_1_4: kmer1_XN_revcomp(kmer2),

where revcomp is a reverse complement function for kmer. Next, competing sequences were constructed for the spacing preference analysis:

spac_m2: kmer1_(X-2)N_kmer2 (this was done if X was greater than 1)

spac_m1: kmer1_(X-1)N_kmer2

spac_p1: kmer1_(X + 1)N_kmer2

spac_p2: kmer1_(X + 2)N_kmer2.

The protein sequence was taken from a previous study⁵¹. Altogether, there were tested 119 PWMs, giving, in sum, up 1,620 structures to analyse. After program runs, the output structures were analysed with code (https://github.com/i-l-sokolov/RosettaFoldNA_output_analysis). In brief, the distance of the closest atoms was calculated for any nucleotide and amino acid. The contact was counted if the distance was less than 0.45 nm. The prediction was considered as true if there were more contacts on the site with sequence extracted from PWM than on the competing site. Extended Data Fig. 9a,b shows the histogram results for described cases. The statistical analysis was done with the SciPy package v.1.10.1 in Python using a two-sided binomial test with a probability of success equal to 0.5. The P values for every group are shown in Supplementary Table 6.

Estimation of the number of composite motif clusters

To estimate the fraction of all composite motifs discovered in this study, we performed two analyses using different similarity metrics and estimation methods. In the first method, we identified 391 clusters of similar motifs using SSTAT Ssum similarity (threshold 1.5 × 10⁻⁵) and then estimated the total number of undiscovered motifs (similarity clusters) by extrapolation using a square-root function.

To build a curve for the number of motif clusters discovered as a function of motif pairs tested, we subsampled the tested motif pairs 300 times. We then fitted a curve to this data using curve_fit functions from SciPy with a p(N) equation:

where A and B are constants, p is the number of clusters and N is the number of pairs. The approximation gives values for A and B of 1.93 and −51.57, respectively, with the approximation shown in Extended Data Fig. 9e,f. The substitution of N with the number of all possible interactions, including self-interactions, is 1,639 × 1,640/2, where 1,639 is the number of transcription factors according to ref. ³. This yields an estimate for the total number of clusters of 2,186. Given that we have found 391 clusters using this threshold, this estimate suggests that we have discovered approximately 18% (391/2,186) of all possible composite motifs.

For the second method, we calculated motif similarity using gapped 10-mer similarity (motifsimilarity program), and then clustered the motifs using the SciPy 1.10.0 Python library using ‘ward’ linkage and (1 – s) as distance between motifs. We then used multiple thresholds for determining the clusters. The threshold range from 0.98 to 1.02 with step 0.001 was studied in detail, as the number of clusters changes markedly in that region. For every subsampled curve, the approximation was done with a linear function using the 50,000th point and last point (Extended Data Fig. 9e,f). Such an approach allows us to estimate the lower bound of the discovered fraction of composite motifs, because the linear function must always be above the real number of clusters. For the final estimation, two final values of thresholds were chosen: 0.999 and 1.000 (corresponding curves are labelled with asterisks). Similarly to above, substitution of N gives us a range of covered motifs between 20% and 48%.

Reporter assays in F₀ mouse embryos

To test whether the identified cooperative TF pairs are responsible for unique transcription programs in distinct cell types, a set of sequences that were preferred by TF pairs, but not by the individual TFs (Supplementary Table 8), were selected. Six copies of the motifs separated by spacer sequences that do not bind to known TFs (from a previous study⁸⁰) were then cloned into a PCR4-Shh::lacZ-H11 vector (Addgene 139098), a LacZ knock-in reporter construct³². To introduce the reporter to the endogenous H11 locus, each of the reconstructed vectors was injected into the pronucleus of FVB embryos together with Cas9 protein (final concentration of 20 ng μl⁻¹; IDT 1074181), sgRNA (50 ng μl⁻¹) in the injection buffer (10 mM Tris, pH 7.5; 0.1 mM EDTA). Mice (FVB and CD-1 strains) were kept in standard housing conditions (temperature 19–23 °C and humidity 40–60%) with food and water provided ad libitum on a reversed 12-h dark–light cycle. Time of gestation was identified by the presence of vaginal sperm plugs, indicating E0.5. Pregnant dams were humanely euthanized, and E11.5 embryos were carefully removed under bright-field stereoscopes in ice-cold PBS (Cytiva, SH30256.01). Both sexes of embryos were presumed to be included. Yolk sacs were collected for genotyping, and successful integration events at the H11 locus were determined by PCR using primers described previously^32,81. This research complies with all relevant ethical regulations. All animal procedures, including those related to generating transgenic mice, were conducted in accordance with the guidelines of the National Institutes of Health (NIH) and approved by the Institutional Animal Care and Use Committee at the University of California, Irvine under protocol no. AUP-23-005.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.