Cooling positronium to ultralow velocities with a chirped laser pulse train

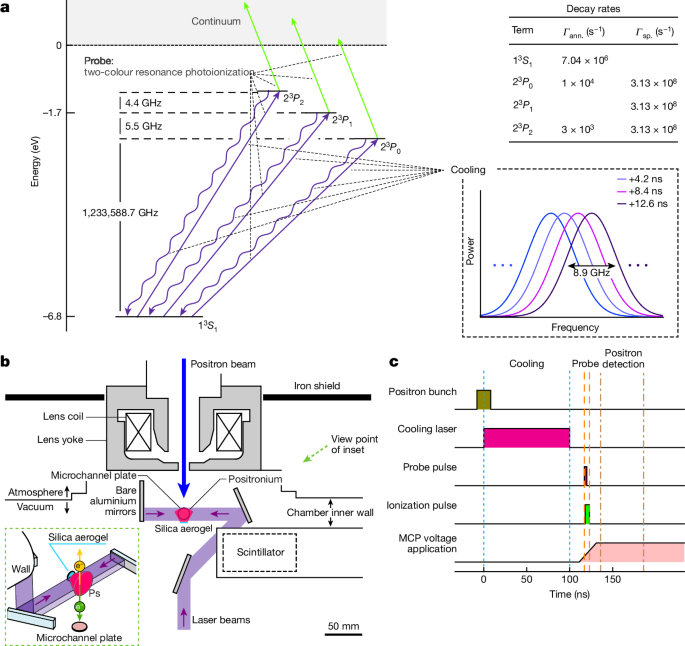
Ps generation

When a positron pulse is injected into certain media, some positrons form Ps and re-emit as Ps into vacuum. These Ps were used in this laser cooling experiment. Positron pulses, with a width of 16 ns and delivered at a repetition rate of 50 Hz (ref. ⁴⁵), contained approximately 10⁶ positrons per pulse. The positrons were transported with an energy of 5 keV from the positron production unit to the experimental station guided by a typical magnetic field of approximately 10 mT generated by coils. By conducting current in the opposite direction only in the last coil, immediately before the experimental station, we minimized the magnetic field in the experimental region. Iron plates for magnetic shielding and the magnetic lens located downstream contributed to this minimization, further reducing the magnetic field in the experimental region to approximately 0.15 mT. This suppresses the Zeeman effect, resulting in a negligible annihilation rate of Ps in the 1³S₁ state (ortho-Ps) due to spin mixing. The transported positrons were focused onto the Ps formation medium using a magnetic lens. Approximately 1% of the incident positrons passed through the magnetic lens, and the remainder collided with the lens and annihilated. The instability in the number of positrons remained at approximately 1% throughout the experiment.

We used a silica aerogel, a three-dimensional network of SiO₂ (silica) nanograins, as the medium for the formation of Ps at room temperature. The silica aerogel had pores with a diameter of 45 nm and a porosity of approximately 95%. The incident angle of the positron bunch on the aerogel was 0° and approximately half the positrons injected into the silica aerogel formed Ps⁴⁶. Some of the long-lived ortho-Ps atoms diffused and came out of the aerogel towards the experimental region. Ortho-Ps atoms decay into γ-rays with a vacuum lifetime of approximately 142 ns and these γ-rays were detected using a LaBr₃(Ce) scintillator and a plastic scintillator. The time-resolved γ-ray flux was measured by observing the current output of the coupled photomultiplier tubes. No influence was detected on the Ps from possible electrostatic charging of the silica aerogel.

Cooling laser

A pulsed laser at 729 nm, which constitutes the backbone of the cooling laser, is called a chirped pulse-train generator⁴³. This is an injection-locked pulsed laser equipped with an intracavity electro-optic phase modulator. It generates a train of approximately 0.1 ns pulses, each with progressively shifting central frequencies. These pulses are then amplified and frequency tripled, producing the 243 nm cooling laser light. The change in the central frequency over time (chirp) can be adjusted by changing the cavity length of the pulsed laser, the driving frequency and the modulation depth of the electro-optic modulator. The duration of the pulse train (the number of micropulses) can also be controlled up to approximately 600 ns, corresponding to a frequency sweep range of approximately 300 GHz using the chirp rate of the present study. Details on the operating principle of the chirped pulse-train generator can be found in ref. ⁴³, and specifics regarding the design and performance evaluation of the cooling laser in this experiment are described in ref. ⁴⁴.

Although the pulse duration has not yet been precisely measured, based on our measurements with an insufficient temporal resolution and the operating principle of the laser, a 0.1 ns pulse duration is estimated. Although an estimate (rather than a precise measurement), it does not affect the discussions in this paper as it is on a timescale considerably shorter than the natural lifetime of the 2P state.

Laser configuration

Ps atoms emitted into vacuum were irradiated by three different pulsed lasers for chirp cooling in the one-dimensional direction as well as measuring the velocity distribution. The laser beams were incident in a direction orthogonal to the positron beam axis and reflected by a bare aluminium mirror in a counter-propagating configuration. The wavelengths of the light pulses used were 243 and 532 nm, with approximately 93% reflectance off the mirror at these wavelengths. The laser irradiation area was approximately 18 mm in the direction of the positron beam axis and approximately 8 mm in the vertical direction perpendicular to the positron beam axis.

The Ps-cooling chirped pulse-train laser was switched on for approximately 100 ns after the positron pulse impacted the silica aerogel. The fluence of a single pulse in an irradiating pulse train was typically 5 μJ cm^–2. During the irradiation period (approximately 100 ns), the central frequency of the light pulse was varied from 1,233,540 to 1,233,590 GHz, with a spectral width for a single pulse of 8.9 GHz (FWHM). The cooling laser was linearly polarized with a polarization direction orthogonal to the positron beam direction.

Doppler spectroscopy

The velocity distribution of the ortho-Ps in the 1S state was evaluated by Doppler spectroscopy using the 1S–2P transition. The Doppler profile of the 1S state was obtained by measuring the signal associated with the number of positrons produced by ionizing the Ps in the 2P state as a function of the probe pulse frequency that resonantly induces the 1S–2P transition. The Doppler shift is indicative of the velocity of Ps along the propagation direction of the laser beam, allowing the evaluation of the ortho-Ps velocity distribution based on the measured Doppler profile. This measurement was conducted approximately 25 ns after the laser cooling ceased, after the complete de-excitation of the 2³P_J-state Ps through spontaneous emission. Doppler spectroscopy was carried out at a 10 Hz repetition rate, and the laser cooling occurred at a 5 Hz rate. By comparing the Doppler profiles before and after laser cooling, changes in the velocity distribution due to cooling can be assessed.

The second harmonic of an optical parametric oscillator (OPO) excited by the third harmonic of a Q-switched neodymium-doped yttrium aluminium garnet (Nd:YAG) laser was used as the probe laser for Doppler spectroscopy. The pulse duration was approximately 3 ns. The optical frequency of the probe laser was swept at approximately 1.2336 PHz and was measured using a wavelength meter with an accuracy of ±3 pm (corresponding to a frequency accuracy of approximately 15 GHz). Because of the longitudinal multimode nature, the spectral width of the second harmonic of the OPO was approximately 1.1 × 10²â€‰GHz. This spectral width was too wide to capture the changes in velocity profile resulting from chirp cooling. Therefore, the second harmonic of the OPO was transmitted through a solid etalon to narrow the spectrum and improve the velocity resolution. The measured transmission spectral width of our custom-made solid etalon available at 243 nm varied from 8 to 16 GHz at FWHM, depending on the angle and position of incidence.

However, the Doppler broadening of Ps without cooling has an FWHM of approximately \(27\sqrt{T}\) GHz at a temperature of T K. This corresponds to a frequency width of 470 GHz at room temperature, which is considerably wider than the narrow resolution. To measure the Doppler profile under uncooled conditions and evaluate the temperature, it was unnecessary to spectrally narrow the second harmonic of the OPO. A greater fraction of Ps with a distributed velocity was resonant, resulting in a larger signal. Therefore, we did not use the solid etalon when measuring the Doppler profile under uncooled conditions.

The typical incident fluences of the laser pulse that induced the 1S–2P transition were 0.27 and 2 μJ cm^–2 with and without spectral narrowing, respectively. This resulted in comparable light spectral densities for these two cases. The polarization of the laser pulse that induced the 1S–2P transition was linear and parallel to the positron beam.

For the ionization laser to photoionize Ps in the 2³P_J state, we used the second harmonic (532 nm) of a Q-switched Nd:YAG laser with a pulse duration of 5 ns. This ionizing laser pulse was delivered with the timing of the intensity peak adjusted to approximately 1.4 ns later than that of the ultraviolet nanosecond pulse, which induced the 1S–2P transition. The irradiation fluence of the 532 nm pulse was typically 15 mJ cm^–2. We set the ionization laser to be linearly polarized parallel to the positron beam, similar to the laser that induced the 1S–2P transition. The repetition rate of the ionizing laser was 10 Hz, same as that of the laser inducing the 1S–2P transition.

Ionized positrons, produced with velocity selectivity from the Ps gas by the two-colour pulsed lasers, were drawn into an MCP. The MCP was placed immediately below the interaction region where Ps and the laser beams interacted. We applied a voltage of −2,000 V to the input surface of the MCP to collect the ionized positrons. The MCP was sensitive to the scattered photons of the deep-ultraviolet laser pulses at a wavelength of 243 nm, which resulted in a large background signal. Therefore, a pulsed negative voltage was applied to the MCP input surface after the completion of cooling laser irradiation, with a rise time of approximately 20 ns. Consequently, the MCP gain remained low at the time when the cooling and probe lasers were incident. This reduces the background signal originating from these photons, enabling the highly sensitive detection of ionized positrons. The voltage at the output plane of the MCP was set to 0 V. The amplified electrons were collected at a metal electrode, to which a constant voltage of 1,000 V was applied. The current output from this electrode was converted to a voltage with a 50 Ω resistor, and its time evolution was recorded. Positron signals were observed in the range of approximately 30–80 ns after the pulse voltage was applied, corresponding to the drift time that is dependent on the Ps location at photoionization. Although the background signal originating from the deep-ultraviolet photons was substantially reduced, a residual signal remained. To subtract this contribution, the ionizing laser was switched on and off every 30 s and we evaluated the signal of ionized positrons based on the difference in the integrated signals of the MCP with and without the ionizing laser.

When the number of Ps in the whole velocity distribution was approximately 3 × 10³ immediately after production, the average number of detected positrons in the frequency-resolved measurements was typically 0.5. Consequently, the uncertainty in the excitation signal in the Doppler spectroscopy measurements was characterized by the randomness in the number of ionized positrons, which is governed by Poisson statistics. To achieve an adequate signal-to-noise ratio, it was necessary to set an appropriate measurement time. For the Doppler spectroscopy used to assess the temperature of Ps gas with a frequency resolution of 110 GHz, the integration time for each probe frequency was approximately 20 min. During this integration time, the number of measurement cycles was approximately 1.2 × 10⁴. In the laser cooling experiment, for which the resolution was set to be an order of magnitude greater and thus the signal was weaker, the integration time was approximately 4 h for each probe frequency. During this time, the number of measurement cycles was approximately 7.2 × 10⁴.

Analysis of the measured Doppler profile of uncooled Ps

We estimated the temperature of the Ps emitted from the silica aerogel using the measured Doppler profile. For this purpose, we defined a model function, which was fitted to the data. The model function describes the number of positrons S(ω_R) generated by the photoionization process from the 2P state as a function of the central angular frequency ω_R of the probe pulse that induces the 1S–2P transition. S(ω_R) is written as

where D(v; T) is the probability density of Ps with velocity v and temperature T (the Maxwell–Boltzmann distribution function is used); I_S is the saturation intensity at the 1S–2P transition angular frequency ω_eg; I(v; ω_R) is the light intensity at the angular frequency resonant to a Ps atom with velocity v; and C is a constant and free parameter in the fitting. The second term in the integral represents the photoionization probability of Ps at velocity v. The functional form for S(ω_R) was determined using the following relation⁵⁵:

which describes the occupation probability of the excited state in a two-level system when irradiated with light of the transition frequency at intensity I_R (see the denominator in the fraction). We used a two-level approximation because we set the spectral width of the probe pulse to be sufficiently wide compared with the splitting in the 1S–2P transition frequency. S(ω_R), determined using P_e, describes the nonlinear responses to the probe laser pulse, such as the Lamb dip and saturation broadening effects in the present Doppler-broadened case.

In our experiment, we directed each laser beam at the Ps in a counter-propagating configuration. Therefore,

where I_L(ω; ω_R) is the intensity spectrum, described as a function of ω, of the probe pulse with its central angular frequency ω_R, and c is the speed of light. We adopted the measured spectral width of I_L(ω; ω_R), with the intensity being a free parameter in the fitting. Here we did not include the spatial distributions of light intensity and Ps density. The light intensity of the probe pulse that reproduced the measurement was consistent with the actual light intensity calculated using the fluence, pulse duration and spectral width. This result demonstrates the validity of the proposed model.

The Doppler profile in the direction normal to the surface of the silica aerogel (Extended Data Fig. 1) was measured by the single-path irradiation of the probe pulse and ionization pulse. These optical pulses (diameter, approximately 10 mm) propagated towards the aerogel 125 ns after the peak timing of the positron bunch. The angles of incidence on the aerogel were 0° for the probe beam and 22° for the positron bunch. The peak of the Doppler profile was observed at a relative frequency of approximately −360 GHz, with an FWHM of approximately 390 GHz. In contrast to the velocity components parallel to the aerogel surface, which are randomly distributed, the distribution of the velocity components perpendicular to the surface cannot be effectively described by a simple distribution function that represents gases or beams. The velocity of Ps moving away from the surface depends not only on its velocity in the generating material but also on its work function. Consequently, the velocity distribution can generally differ from the component parallel to the surface. For these reasons, we did not perform an evaluation by fitting the experimental data. Irrespective of the parallel or perpendicular direction to the surface, the emission velocity of Ps changes dynamically with the reduction in momentum due to scattering with the molecules comprising the aerogel, with the velocity distribution also being influenced by the decay due to the Ps lifetime.

Analysis of fractional change in Doppler profile using a phenomenological model

We analysed the fractional change in the velocity distribution induced by the cooling laser by fitting the following phenomenological model to the data: the fractional change for S_on(f) and S_off(f) is defined as

We first used the following raw functions that did not include the frequency resolution in the experiment:

where the argument f is the relative frequency, f₀ is the 1³S₁–2³P₂ transition frequency of Ps, m_Ps is the mass of Ps, k_B is the Boltzmann constant and T₀ is the temperature of Ps released from the silica aerogel. On the basis of the experimental results, we assumed that the Doppler profile of the uncooled Ps was a Maxwell–Boltzmann distribution at temperature T₀ = 600 K. The following free parameters used in the fit describe the change in Doppler profile associated with cooling: f_cooled is the Doppler shift corresponding to the optical frequency at the beginning of the cooling laser; Δf is the Doppler width of the decelerated component; S_cooled is the signal level after cooling in the spectral region swept by the chirped cooling laser; A characterizes the magnitude of the decelerated component signal. These raw functions are plotted in Extended Data Fig. 2.

We generated model functions S_on(f) and S_off(f), which correspond to the experimental results obtained, by convolving \({S}_{\text{on}}^{\text{raw}}(f)\) and \({S}_{\text{off}}^{\text{raw}}(f)\) with the frequency resolution due to the linewidth of the probe pulse. The change in Doppler profile associated with cooling was quantitatively evaluated by fitting the modelled fractional change to the measured fractional changes. In Extended Data Fig. 2, \({S}_{\text{on}}^{\text{raw}}(f)\) is plotted using the parameters obtained from the fit.

The fitting parameters varied with the spectral width of the probe pulse, which determined the frequency resolution of the measured Doppler profile. When the spectral width, which varied in the experiment, was set to 8 GHz (narrowest), the widest Doppler spread of the cooling component was evaluated. In the main text, we have shown the corresponding best-fit value (23 GHz) and upper statistical limit (30 GHz) as conservative estimates (the upper statistical limit of the width of the cooled component was evaluated at the 95% confidence level). The population reductions in the cooled spectral region were estimated to be 61% and 49%, respectively. For a spectral width of 16 GHz for the probe pulse, the best-fit value and the upper limit of the width of the cooled component were 18 and 27 GHz, and the corresponding population reductions were 78% and 61%, respectively.

We believe that the estimated population reductions were smaller than those expected from population reduction by laser cooling alone, due to the influence of delayed Ps release from the silica aerogel. Such delayed release from porous materials has been reported previously⁵⁶. Our empirical observations suggest the presence of Ps emitted from the silica aerogel several tens of nanoseconds after the injection of the positron bunch, when we observed the components of zero lateral velocity. However, we cannot quantitatively discuss the delayed fraction due to the absence of available systematic data.

Evaluation of the frequency resolution in the laser cooling experiment

The frequency resolution of the fractional change in the Doppler profile as a result of laser cooling was determined using the spectral width of the probe pulse and intensity-dependent saturation broadening. We evaluated the spectral width of the probe pulse using the optical resolution of the Fabry–Pérot solid etalon used for spectral narrowing. The FWHM optical frequency resolution as a function of the angle of incidence is shown in Extended Data Fig. 3. The resolution was evaluated by measuring the transmission spectrum of single-longitudinal-mode laser pulses at 243 nm. The spectral width of the pulses is expected to be less than 10 MHz, which is considerably narrower than the designed frequency resolution of the solid etalon, thereby enabling the evaluation of the actual resolution. We measured the transmittance as a function of the angle of incidence of the etalon. All the incident angle sweeps designated in the legend were performed in the direction of increasing angle. These three sets of measurements were performed in the experimental period but not consecutively.

The results indicate that although the transmission spectral width tends to increase with the angle of incidence, it varies widely for each measurement. The degree of variation exceeds the measurement uncertainty, suggesting that the conditions of the etalon changed with each sweep. The possible characteristics of the solid etalon that can cause such variations include non-uniform thickness and inhomogeneous strain on the etalon. Variations can then occur because the position of the laser irradiation on the solid etalon cannot be completely fixed. To detect a change in the Doppler profile resulting from laser cooling, the angles of incidence of the probe pulse on the etalon were set in the range tested above, resulting in the same degree of variation in the linewidth of the probe. Therefore, we estimated the spectral width of the probe pulse to be 8–16 GHz, based on the measured range of values shown in Extended Data Fig. 3.

Next, we examined the influence of saturation broadening, which also affects the frequency resolution. Using the effective intensity calculated from the fluence, pulse duration and spectral width of the spectrally narrowed probe pulse, the degradation of the frequency resolution owing to saturation broadening was at most 1 GHz. Thus, saturation broadening can be neglected.

We considered the 8–16 GHz range of the frequency resolution as a systematic uncertainty in the evaluation of the fractional change. Hence, a conservative effective temperature was evaluated.

Allowed 1³
S–2³
P transitions and their intensities

Here we describe the allowed transitions and their intensities among the 1³S–2³P transitions used for laser cooling and Doppler spectroscopy. The transition matrix element is

where d is the electric dipole moment; E is the electric field of light; n, L and S are the principal quantum number, orbital angular momentum and total spin angular momentum, respectively; J and M are the total angular momentum and its projection along the quantization axis, respectively. Subscripts e and g indicate the excited and ground states, respectively.

The electric dipole moments, when we define the quantization axis of the atomic orbitals as the z axis, are shown in Extended Data Fig. 4a,b. The direction of projection of the electric dipole moment is shown at the top of each diagram. The allowed transitions induced by the electric field of light with the corresponding polarization vectors are represented by arrows. The numbers associated with the arrows indicate the square of the absolute value of each component of the electric dipole moment normalized to the following constant:

where e is the elementary charge and a₀ is the Bohr radius. For some transitions, the numbers are omitted because the absolute values of the electric dipole moments coincide with those of the other transitions that differ only in the sign of M. The transition rates are proportional to the values shown in Extended Data Fig. 4a for linearly polarized light parallel to the z axis, and in Extended Data Fig. 4b for orthogonally polarized light. In our experiment, the polarizations of the cooling laser pulse and probe laser pulse in Doppler spectroscopy were linear and orthogonal to each other. Extended Data Fig. 4a,b can be used to evaluate the transition intensity of each pulse.

Extended Data Fig. 4c shows the spontaneous emission rates from the excited states to each ground state normalized by the total decay rate Γ_sp. ≅ 3.13 × 10⁸ s^–1 from each excited state. By symmetry, the spontaneous emission rates from the states with negative M_e values, which are omitted from the table in Extended Data Fig. 4c, are equal to the corresponding rates between the states with the signs for M_e and M_g reversed.

Extended Data Fig. 4a–c shows that in the cooling process, during which the transitions are repeated many times, it is important to use a cooling laser with a spectral width comparable with the splitting in the transition. Otherwise, if we repeat the cooling cycle by transitioning to the 2³P₀ and 2³P₁ states, for example, the 1³S₁ state becomes polarized and eventually makes transitions to these excited states dark. Moreover, the 1³S₁–2³P₂ transition dominated the 1S–2P transitions. Therefore, we present our experimental results as functions of frequency relative to the 1³S₁–2³P₂ frequency difference. Note that the resonance frequency observed at the one-photon transition is approximately 3 GHz higher than this frequency difference owing to the conservation laws of energy and momentum.

Numerical simulation

We evaluated the time evolution of the momentum distribution of Ps under the influence of a cooling laser based on the Lindblad master equation:

where t, ħ, H and L(ρ) are the time, Dirac’s constant, Hamiltonian and Liouvillian, respectively. We considered the density matrix ρ in the space spanned by the simultaneous eigenstates of the momentum of Ps and atomic configurations in the L–S coupling scheme. The interaction between Ps and the photon field was incorporated as an electric dipole interaction. This framework can describe the transitions between atomic orbitals through absorption, stimulated emission and spontaneous emission processes, as well as momentum changes because of photon recoil. We incorporated the relaxation of Ps due to annihilation processes into the master equation as a longitudinal relaxation process.

Using the simulated velocity distribution shown in Fig. 3a, we can simulate the fractional change (Fig. 2b). The simulated Doppler profiles with and without the cooling laser irradiation were convolved by the spectral resolution to obtain \({S}_{\text{on}}^{\text{sim}}(\,f)\) and \({S}_{\text{off}}^{\text{sim}}(\,f)\), respectively. The spectral width of the probe pulse determines the spectral resolution. The argument f is the relative frequency, which is the first-order Doppler shift calculated from the velocity of Ps. To express a part of the probed Ps atoms, which interacted with the cooling laser, we introduce an uncooled Ps fraction r. The fractional change can then be calculated as \((1-r)\frac{{S}_{\text{on}}^{\text{sim}}(\,f)-{S}_{\text{off}}^{\text{sim}}(\,f)}{{S}_{\text{off}}^{\text{sim}}(\,f)}\). The parameter r was determined by fitting this function to the measured data. Figure 3b compares the measured and simulated fractional changes. The filled circles are identical to those shown in Fig. 2b. The thickness of the curve was determined on the basis of the frequency resolution in the range of 8–16 GHz. The measured data were well reproduced, with the best estimated r ranging from 0.18 to 0.40 and the spectral resolution shown above. The statistical uncertainty of the estimated r is typically 0.06 at the 1σ confidence level. The resultant fraction r is reasonable under the experimental condition, and its consistency with the measured data supports the successful demonstration of the laser cooling of Ps.

Extended Data Fig. 5 presents the corresponding Doppler profiles mentioned above. Similar to the experiment, the simulation evaluated the Doppler profiles 125 ns after Ps formation, following 100 ns of cooling laser irradiation. Components resonating with the frequency-swept cooling laser were decelerated and concentrated in the frequency domain corresponding to zero velocity. Compared with the case without cooling, the slow components showed a threefold increase. No change was observed in the detuned components, which did not resonate with the cooling laser.

To illustrate the parameter design of the cooling laser in this study, we present typical examples of cooling time dependence and chirp rate dependence based on the simulations constructed here. Extended Data Fig. 6a displays the momentum distribution after cooling, evaluated as a function of cooling time while keeping the chirp rate constant. The optical frequency detuning of the cooling laser at the end of cooling was set to −9 GHz. As the cooling duration is extended, the sweep frequency range of the cooling laser increases, thereby enhancing the contrast in number between the cooled and uncooled components. However, due to the lifetime effects of Ps, the number of cooled atoms is found to decrease compared with shorter cooling times. The maximum number of cooled atoms is achieved at a cooling time of approximately 100 ns, which is the duration used in this study.

Extended Data Fig. 6b shows the momentum distribution after cooling when the chirp rate is varied, with the cooling time fixed at 100 ns. When the chirp rate exceeds the rate characterized by the recoil frequency associated with photon absorption and the natural emission rate, the proportion of atoms that cannot maintain the chirp cooling cycle increases, resulting in decreased efficiency. Note that this calculation assumes that the entire volume of the Ps gas is constantly exposed to the cooling laser.