Continuous-variable multipartite entanglement in an integrated microcomb

The basic units of quantum information are quantum bits (qubits) or quantum modes (qumodes). They can be physically represented in discrete-variable or continuous-variable quantum systems, for example, optical, atomic, superconducting and mechanical systems. A key objective is to entangle a large number of qubits or qumodes. Achieving large-scale entanglement of light is pivotal for advancing quantum technologies in computation¹, networking² and metrology³. Universal optical quantum computation can be achieved by a sequence of measurements performed on large entangled cluster states^21,22. With light, qubits are typically encoded in discrete modes of single photons²³, whereas qumodes are encoded in continuous quadratures of light fields²⁴. Discrete-variable encoding in single-photon allows ultrahigh-fidelity qubit operations but currently faces challenges in deterministic qubits generation and entanglement. It has led to impressive demonstrations of quantum information processing in discrete-variable experiments using probabilistic multi-qubit entanglement²³. By contrast, continuous-variable encoding in light quadratures allows for deterministic generation and entanglement of qumodes, at the expense of lower fidelity. The multiplexing of light in various degrees of freedom, for example, path^25,26, time^27,28, frequency^29,30,31 and spatial eigenmodes^32,33, presents a promising approach to creating large-scale continuous-variable cluster states.

Integrated quantum photonics is a versatile platform that can on-chip encode, process and store quantum information of light^4,5. Discrete-variable integrated quantum photonics (DVIQP) technologies have yielded integrated sources, circuits and detectors for single photons^6,34, multi-qubit genuine entanglement^7,8, as well as proof-of-principle demonstrations in quantum computing^9,10 and networking¹¹. Continuous-variable integrated quantum photonics (CVIQP) is anticipated to provide high complexity, phase stability, precise mode matching, mode-cleaning-free and low interfacing loss, throughout the generation, manipulation and detection of quadratures of light. Recent advancements in integrated photonic materials and technologies have markedly progressed CVIQP. It includes the observation of single-mode and two-mode quadrature squeezed states (that is, Einstein–Podolsky–Rosen, EPR, states) in optical waveguides^12,13,14, circuits^15,16 and microresonators^17,18,19. Multiple pairs of two-mode EPR states have been demonstrated in a squeezer array for Gaussian boson sampling^35,36 and in a single microresonator-based frequency comb in which only two-mode entanglement is produced²⁰. Recently, second-order single-photon correlations have been studied in soliton microcombs, which implies underlying multimode entanglement dominated by spontaneous parametric processes³⁷. However, the generation and detection of continuous-variable multi-qumode or multipartite entanglement remain unknown in integrated quantum photonic platforms.

Here we report the first generation of continuous-variable multipartite entanglement on an integrated-optical quantum chip. An integrated-optical microresonator-based frequency comb (that is, microcomb) was operated to generate multimode Gaussian states in the below-threshold quantum frequency modes. The inseparability of eight frequency qumodes was demonstrated by violating the positive partial transposition (PPT) criteria. We show that, owing to the Bragg scattering effect in the microcomb, multipartite entanglement with cluster-type structures cannot be directly generated in the frequency modes but rather in the supermodes, distinguishing the mechanics of multipartite entanglement in the microcomb from that in second-order squeezing processes. A coherent polychromatic pump-detection (CPPD) technique was adopted for the preparation, manipulation and measurement of multipartite entanglement with phase coherence throughout the system. Using experimental violations of the van Loock–Furusawa criteria, we validated the generation of various supermode multipartite entanglement. By the measurement of the full matrices of nullifier correlations with total off-diagonal correlations amounting to approximately 4–8% of diagonal correlations, we characterized entanglement structures of the generated states, which are approximate to the corresponding cluster-type structures for finite squeezing. Also, quadrature squeezing and multipartite entanglement were detected across broad sideband frequencies. Our results indicate the possibility of generating and processing large-scale entanglement on CVIQP chips for scalable photonic quantum technologies.

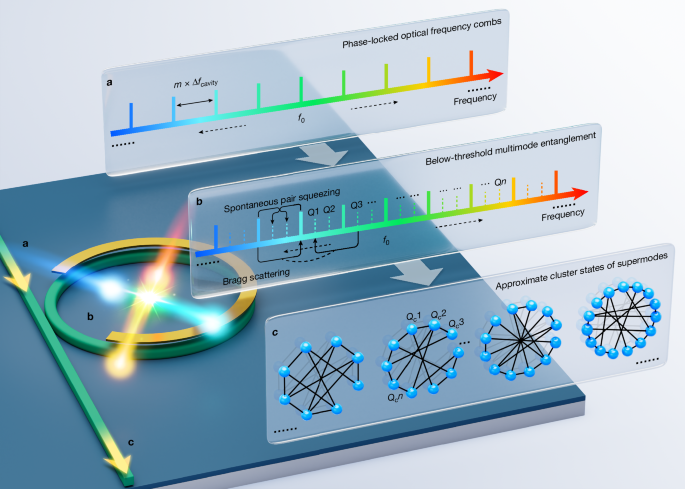
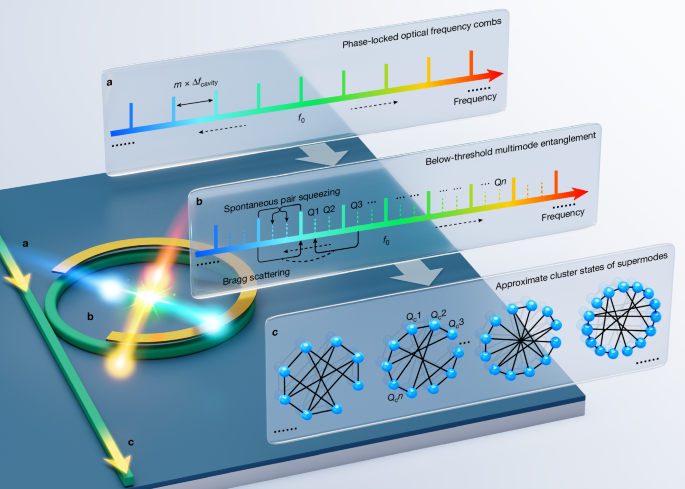
Figure 1 shows the processes to generate continuous-variable multipartite entanglement with approximate cluster-type structures in the integrated microcomb. When the microresonator is pumped by synchronous phase-locked polychromatic beams^29,30, parametric nonlinear-optic processes below the oscillation threshold can lead to the generation of quantum frequency squeezed vacuum modes. Taking the mean-field approximation for the bright pumping beams, the interacting Hamiltonian of quantum modes can be written as³⁷

where \(\delta _1=\delta _\omega _k+\omega _l,\omega _i+\omega _j\) and \(\delta _2=\delta _\omega _i+\omega _k,\omega _j+\omega _l\) represent simplified phase matching conditions for the spontaneous pair squeezing (SPS) and Bragg scattering (BS) processes, respectively, κ is the nonlinear coupling coefficient, A_i is the classical amplitudes of pumps and \(\widehata\) and \(\widehata^\dagger \) represent the bosonic operators of qumodes. Notably, the presence of the Bragg scattering process (that is, absent in second-order nonlinear processes) makes a substantial difference when generating continuous-variable multipartite entanglement. In the microcomb, the distribution of intrinsic squeezing of multimode Gaussian states at different sideband frequencies is governed by the quantum Langevin equations³⁸:

where \(\widehat\bfx=(\widehatq_1,\widehatq_2,\ldots ,\widehatq_n^\rmT\) is the vector of quadratures, \(\widehatq_k=\widehata_k^\dagger +\widehata_k,\widehatp_k=i(\widehata_k^\dagger -\widehata_k),\widehat\bfx_\rmin\) is the quadrature vector of input fields that satisfy the input–output relation \(\widehat\bfx_\rmin(t)+\widehat\bfx_\rmout(t)=\sqrt2\varGamma \widehat\bfx(t)\), \(M=i[\widehatH_int,\widehat\bfx]/\hbar \) and Γ = diag(γ₁, γ₂, …, γ_n∣γ₁, γ₂, …, γ_n) are the gain and damping matrices, respectively.

a, Coherent polychromatic phase-locked optical frequency combs (solid lines) are adopted to externally excite an integrated optical microresonator. b, In the microresonator, Kerr nonlinear-optic processes take place that operate below the threshold of parametric oscillation, and quantum frequency modes (Qi, dotted lines) are emerging in the microcombs. The FSRs of pump combs and microcombs satisfy Δf_pump = mΔf_cavity (where m is an integer). The microresonator can be controlled by an upper microheater to match the pump combs. The parametric processes, including spontaneous pair squeezing and Bragg scattering in the microresonator, result in the generation of complex Gaussian states of quantum frequency modes, which can be linearly transformed to the eigen-supermodes (that is, Q_e1, Q_e2, … Q_en, a superposition of frequency modes) with marked intrinsic squeezing, and further generate the supermode-based multipartite entangled states with various cluster-type structures. c, Approximate cluster-type states of multiple supermodes (that is, Q_c1, Q_c2, … Q_cn) can be generated. The structure of multipartite entanglement can be reconfigured by tailoring the configurations of polychromatic pump beams and the measurement bases of local oscillator beams. In the graphical representation of multipartite entangled states, blue vertexes represent supermodes and black edges all equal to 1 represent deterministic entanglement.

In Fig. 1, feeding excitations by large-number phase-locked synchronous polychromatic beams, for example, from one external coherent optical frequency comb, large-scale entangled multimode Gaussian states could be generated in the microcomb. Instead of directly detecting the entanglement structure in the frequency comb modes (Q), we extract the eigen-supermodes (Q_e) and use them to generate multimode cluster-type states with various structures in corresponding supermodes (Q_c). The supermode can be regarded as a superposition of frequency comb modes up to a linear transformation³⁰. Measuring the states on the basis of eigen-supermodes, intrinsic quadrature squeezing and the degree of multimode entanglement can be characterized, which is carried out by polychromatic homodyne detections by tailoring the local oscillator beams. Moreover, entanglement structures can be reshaped by reconfiguring linear-optical Gaussian transformations through the polychromatic local oscillators^39,40, together with dedicated controls of the polychromatic pumps. The CPPD method enables precise and efficient generation, manipulation and measurement of large-scale entanglement in the frequency domain. In this study, we benchmark that with eight frequency qumodes as an example. The procedure for the generation, manipulation and measurement of supermode multipartite entangled states with various structures is provided in Supplementary Information section 2.1.

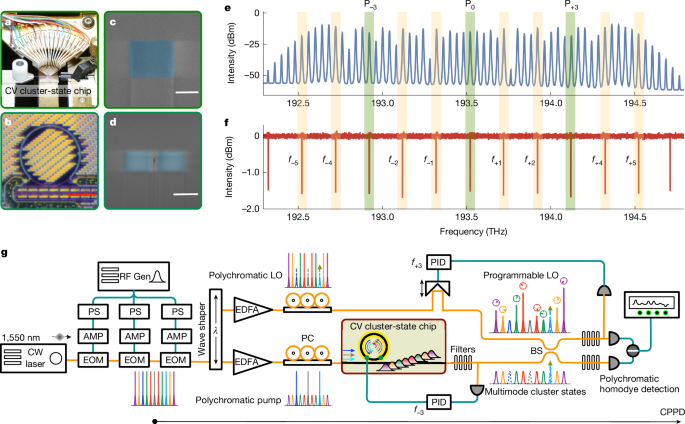
Figure 2a–d shows the quantum microcomb device fabricated in silicon nitride nanophotonic waveguides. It is considered an interesting integrated quantum photonic platform, possessing low optical loss, strong third-order nonlinearity, dense integration and complementary metal-oxide–semiconductor compatibility^35,41,42,43. In the microring resonator, an anomalous dispersion is achieved by tailoring the structural dispersion of the waveguide (Supplementary Fig. 1). A large mode spacing of about 200 GHz free spectral range (FSR) enables well separation of combs, suppressing parametric fluorescence noises and non-parametric effects. Overcoupling is used to efficiently extract (about 90%) squeezed light out of the cavity. A high intrinsic quality factor of 1 million is measured in Supplementary Fig. 1. In the experiment, the microring is tuned by an upper thermo-optical resistive microheater, to lock the resonant frequencies (Fig. 2f) to the frequencies of electro-optic (EO) pump combs (Fig. 2e), which were produced by modulating an ultralow noise laser at 1,550.245 nm (193.518 THz). The comb spacing of electro-optic combs is aligned with the mode spacing of microcombs having Δf_cavity = 5Δf_EO.

a, Photograph for chip carrier. The chip is fibre-coupled in and out using lensed single-mode fibres. The integrated microheater is controlled by d.c. probes. b, Optical microscope image for a fabricated silicon nitride microring microresonator with a radius of 114 μm. c,d, False-colour scanning electron microscope images for single-mode waveguide with a cross-section of 1 μm × 800 nm, and a 400-nm gap between bus waveguide and microring. e,f, Measured spectra of electro-optic combs and the microring with an FSR of 39.98 GHz and 199.9 GHz, respectively. In the electro-optic combs, lights at the frequencies of P_±3,0 are selected as pumps (green windows), whereas those at f_{±1,±2,±4,±5} (orange windows) are selected as the local oscillator beams. In the microresonator, below-threshold multimode Gaussian states are generated at the frequencies of f_{±1,±2,±4,±5}. g, The CPPD experimental setup. A low-noise continuous-wave (CW) laser at 1,550 nm is modulated by three cascaded EOMs to produce electro-optic combs. One wave-shaper is used to tailor the pump and local oscillator beams. Three pumps are used to synchronously excite the microcomb to generate the multimode Gaussian states. Polychromatic homodyne detections, in which the local oscillators are reprogrammed with intensities and phases, are adopted to characterize and reconfigure the multipartite entangled states of supermodes. Quantum noises are recorded using a spectrum analyser. The polychromatic pumps and polychromatic local oscillators for homodyne detections are split from the same electro-optic comb, so that they are highly coherent throughout the system. RF Gen, radio-frequency generator; EOM, electro-optic modulator; AMP, electronic amplifier; EPS, electronic phase shifter; PC, polarization controller; EDFA, erbium-doped fibre amplifier; PID, proportional integral derivative; BS, fibre beamsplitter; CV, continuous variable. Orange lines indicate single-mode optical fibres and blue lines indicate electric cables. Scale bars, 100 μm (b); 500 nm (c); 1 μm (d).

Source Data

Figure 2g shows the CPPD experimental setup. The use of polychromatic pump and polychromatic homodyne detection technologies^30,31 played a crucial part in creating the first (to our knowledge) integrated-optic continuous-variable multipartite entanglements specifically implemented in the frequency domain, rather than others. Our CPPD combines these advanced technologies to achieve global phase-locking throughout polychromatic pumping and detection processes. Using a wave-shaper, the electro-optic combs of P_±3,0 serve as phase-locked pumps for synchronously polychromatic pump, whereas the combs of f_{±1,±2,±4,±5} serve as the local oscillators for polychromatic homodyne detection. The phases of the squeezed and local oscillator beams are inherently stable because of the coherent nature of the electro-optic combs. Moreover, the comb at f₊₃, interfering with the post-beam splitter, is repurposed as a reference for globally locking the relative phase between the local oscillators and squeezed beams. This method enables precise measurements of quadrature squeezing, multimode entanglement and a comprehensive characterization of the covariance matrix of the generated states, all within a unified global phase-locking reference frame. In the experiment, monochromatic, bichromatic and polychromatic homodyne detections were implemented by tailoring the intensities and phases of local oscillators (Supplementary Fig. 3). We choose 5 MHz as the basic sideband frequency in an experiment to accurately characterize quadrature squeezing and multipartite entanglement. More details are provided in Supplementary Information section 1.

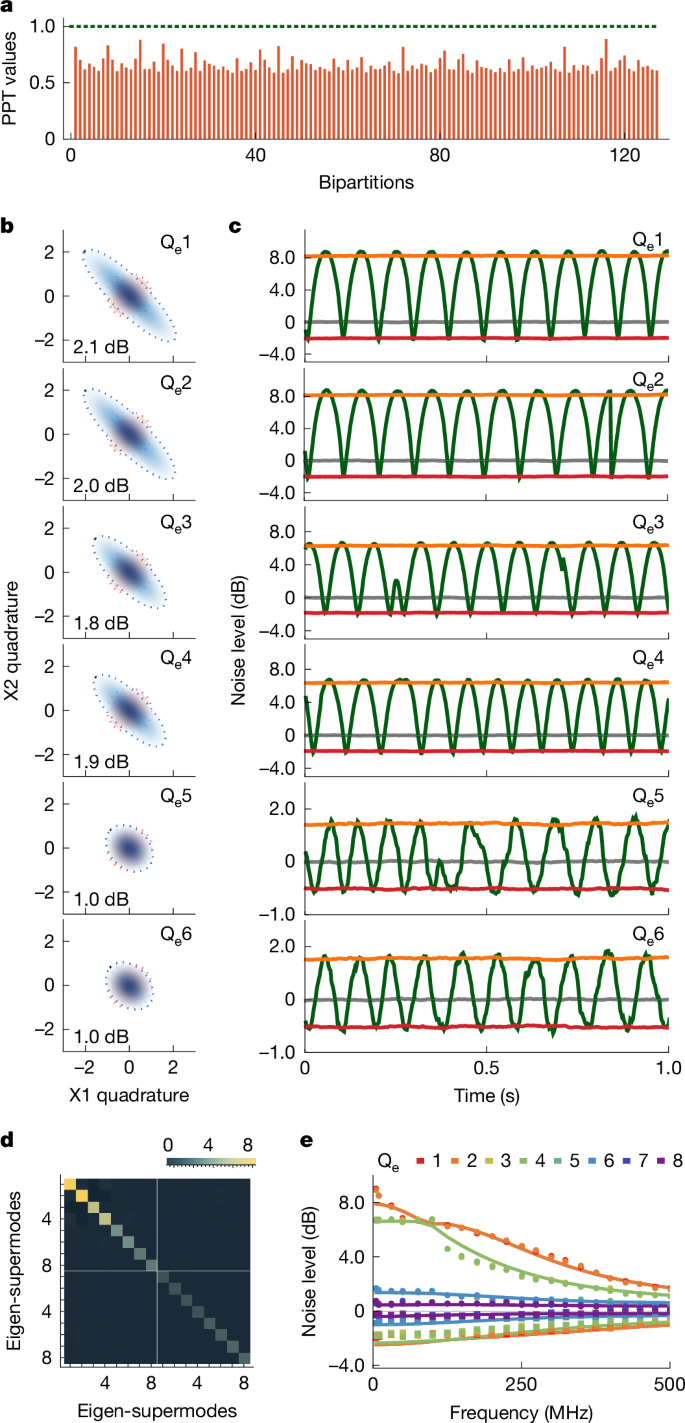
We first verify the entanglement of eight frequency modes by the experimental violations of the continuous-variable version of PPT criteria⁴⁴. If a state of the composite system can be decomposed into a product state of two subsystems, partially transposing one subsystem will still generate a physical state with symplectic eigenvalues greater than or equal to one. Conversely, if the partially transposed state has a symplectic eigenvalue less than one, the original state is proven to be inseparable. There are in total 127 different bipartitions for the eight-qumode Gaussian states, including 1 × 7, 2 × 6, 3 × 5, 4 × 4 bipartitions. Figure 3a shows the symplectic eigenvalues for their partially transposed states, estimated from the measured covariance matrix in the frequency modes, as shown in Supplementary Fig. 4). For all 127 bipartitions, the symplectic eigenvalues are less than one, which indicates that the eight-qumode state cannot be decomposed into any direct product of two separate subsystems. Violating the PPT criteria, therefore, demonstrates the presence of multipartite entanglement. The intrinsic eight-qumode state on-chip is also expected to possess much stronger entanglement (Supplementary Fig. 7).

a, Experimental symplectic eigenvalues for all bipartitions of the eight-mode Gaussian state in the frequency comb modes. All symplectic eigenvalues are estimated to be below 1 (green dotted line), experimentally violating the PPT criteria for all bipartitions. b, Phase diagram for the six dominant eigen-supermodes (that is, Q_e1–Q_e6). Blue ellipses represent the quadrature squeezing and anti-squeezing, whereas red circles represent vacuum fluctuations. c, Direct experimental measurement of noise powers for the six eigen-supermodes. Grey lines indicate the shot noise level, green lines are noise curves measured by periodically ramping the local oscillator phase. The red lines are measured by squeezing with locked phases and the orange lines are measured by anti-squeezing with locked phases. d, Measured covariance matrix for the eight eigen-supermodes (that is, Q_e1–Q_e8). The matrix is coded by colours with the key at the top. e, Quadrature squeezing and anti-squeezing of eight eigen-supermodes at different sideband frequencies. Points are experimental data, and lines are theoretical results of equation (2). The supermodes are doubly degenerate in theory, whereas they are experimentally discernible (indicated by those points with two similar colours). Data in a–d were collected at the 5 MHz sideband frequency.

Source Data

Applying the Bloch–Messiah decomposition of the measured covariance matrix in Supplementary Fig. 4, we extracted the eigen-supermode bases. In the experiment, we carried out polychromatic homodyne detection to directly characterize squeezing for all the eight eigen-supermodes. For example, Fig. 3b,c shows the measured results for the six dominated squeezed eigen-supermodes selected to prepare multipartite entanglement with cluster-type structures. It acquires four supermodes with about 2 dB squeezing (on-chip 6 dB), and two supermodes with about 1.0 dB squeezing (on-chip 2.6 dB). The intrinsic on-chip squeezing in each supermode and the configuration of LO combs in polychromatic detections are provided in Supplementary Fig. 4. The measured full covariance matrix of all eight eigen-supermodes is reported in Fig. 3d, showing the essential orthogonality of supermodes with minimal off-diagonal terms, crucial for generating and validating multipartite entangled states. We remark that, in the frequency modes, the covariance matrix in Supplementary Fig. 4 exhibits strong off-diagonal correlations, stemming from the intrinsic Bragg scattering effect in the microcomb, which implies direct generation of multipartite entanglement with cluster-type structures is unattainable in the frequency modes through any Gaussian local unitaries^45,46 (Supplementary Information section 2.4). Instead, the generation of such entanglement can occur in the supermodes of the microcomb, by applying non-local multimode operations on the selected eigen-supermodes (Supplementary Information section 2.1 and Supplementary Fig. 5). Results in Fig. 3 indicate an instance of multimode squeezing, whereas the squeezing strengths of eigen-supermode squeezers would be tailored by reconfiguring the polychromatic pumps for various entanglement structures.

Applying linear operations on the eigen-supermode squeezers shown in Fig. 3b allows arbitrary preparation of supermode cluster states with various entanglement structures for infinite squeezed Gaussian states³⁹. In practice, owing to finitely squeezed states, it allows for the creation of approximate cluster states, provided the squeezing strengths for the squeezer array can be finely adjusted to match their optimal distribution (Supplementary Information section 2.1). The continuous-variable cluster states in the limit of infinite squeezing can be defined as the multimode Gaussian states \((\widehatp_i-\sum _j\mathcalV_ij\widehatq_j)\to 0,i,j\in G\), where G is a graph whose vertices represent qumodes and edges represent entanglement, and adjacent matrix ν determines the entanglement edge, as shown in Fig. 1. The nullifiers \(\mathcalN_i\) for cluster states are defined as

where the subscript c denotes the transformed Q_c supermodes. In our experiment, we linearly operated the polychromatic local oscillators (equivalent to applying linear transformations on the multimode Gaussian states³¹) and finely tailor the intensity and detuning of polychromatic pumps to obtain the theoretically acquired squeezing strength of eigen-supermode squeezers, so as to prepare multipartite entanglement with cluster-type structures.

We then verify the violations of the van Loock–Furusawa inequalities⁴⁷ for multipartite entangled states with different entanglement structures:

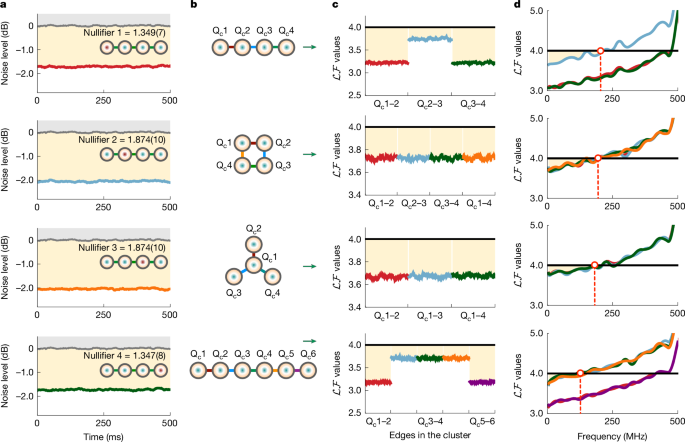
where the \(\mathcalLF\) represents the van Loock–Furusawa values measured in experiment. Figure 4a reports the four measured nullifiers (normalized to vacuum fluctuations) for the four-supermode entangled state with the linear-type entanglement structure. The nullifier variances 1.349(7), 1.874(10), 1.874(10), 1.347(8) are obtained. The values in parentheses is  ±1σ uncertainty. This results in experimental violations of all the three van Loock–Furusawa inequalities with values of 3.223(13), 3.748(17), 3.221(13) in Fig. 4c. The violations of inequalities successfully demonstrate linear-type multipartite entanglement structure. Moreover, we experimentally measured the nullifiers and inequalities for the four-supermode box- and star-type entanglement structure, and the six-supermode linear-type entanglement structure, as shown in Fig. 4b. Results of measured \(\mathcalLF\) are reported in Fig. 4c. It is verified that multipartite entangled states, up to six supermodes, with different entanglement structures can violate the inequalities. The full set of nullifiers and inequalities as well as their experimental results are provided in Supplementary Table 2.

a, Direct experiment measurement of noise powers for the four nullifiers of the linear-type entanglement structure. The nullifier variances 1.349(7), 1.874(10), 1.874(10), 1.347(8) are normalized to the shot noise (grey lines) with a rescale number of 2, 3, 3, 2, respectively. Values in parentheses are ±1σ uncertainty, each of which is estimated from a full set of 400 data points. The grey regime above the shot noise represents the absence of squeezing, whereas the orange regime represents the presence of strong squeezing. b, Graphical representations of various cluster-type entanglement structures in supermodes (Q_ci), including the linear-, box- and star-type entanglement structures. c,d, Experimentally measured \(\mathcalLF\) values at the 5 MHz sideband frequency in c and at different sideband frequencies in d, for the corresponding entangled states. If the measured \(\mathcalLF\) value is less than 4, the inequality is violated. Coloured data in c and d represent measured inequalities for different edges in b. If all inequalities are violated for all edges, we confirm the successful generation of multipartite entanglement. In c and d, in the orange regimes, all of the van Loock–Furusawa inequalities are experimentally violated, demonstrating the presence of multipartite entanglement at broad frequencies.

Source Data

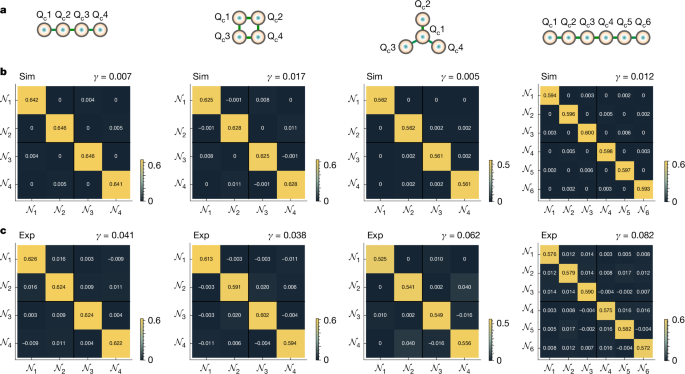
Moreover, as the violations of inequality (equation (4)) are insufficient for characterizing the full entanglement information in the generated states, especially for finite squeezing⁴⁶, we conducted a comprehensive analysis by measuring the full matrices of nullifier correlations for the inferred on-chip states. The results are shown in Fig. 5. It shows that the off-diagonal correlations are sufficiently lower than the diagonal correlations. This is a result of the precise adjustments made to the pump configurations to match the squeezing strength of squeezers for different states. To quantify the extent of additional hidden entanglement that may not be captured within the cluster structures of the generated states, we introduce a γ-factor that describes a suppression of the summed off-diagonal correlations in comparison to the diagonal correlations:

where \(| \rmcov(\mathcalN_i,\mathcalN_j)| \) represent the absolute value of nullifier correlations. With the optimized squeezing distribution, the correlation matrices and corresponding γ values of 0.058, 0.048, 0.101, 0.109 reported in Fig. 5c are measured for the four generated states in our experiment, which match with the simulation results in Fig. 5b derived from the measured squeezing distribution of the eigen-supermodes. The simulation results in Fig. 5b indicate the optimal achievable values of γ to be 0.007, 0.019, 0.006, 0.016 for the current experimental pump configurations. The discrepancy from the diagonal matrices in theory arises from slight deviations in the configurations of polychromatic pumps and polychromatic local oscillators from their ideal settings. These results indicate that the cluster structures efficiently capture almost all the entanglement information in our experiment, closely approximating the characteristics of the corresponding cluster-type states. Future enhancements to the experimental system will enable a more accurate characterization of the generated multipartite entanglement. Details are provided in Supplementary Information sections 2.1 and 3.3.

a, Graphical representations of the linear-, box- and star-type entanglement structures. The transformed supermodes are denoted by Q_ci. b, Simulation results. c, Experimental results of full matrices of nullifier correlations for the on-chip generated entangled states with linear-, box-, and star-type entanglement structures. Simulation results are estimated from the measured squeezing distribution of eigen-supermodes for each entanglement structure. All matrices closely resemble an identity matrix scaled by a constant λ, as shown in Supplementary Table 1. The corresponding γ values, displayed at the top, indicate sufficiently lower off-diagonal correlations compared with diagonal correlations in our simulation and experiment. The nullifier correlation matrix is coded by colours by its absolute value (\(|\,\rmcov\,(\mathcalN_i,\mathcalN_j)|\)) and the key is provided at the bottom right. The value of each element is explicitly shown for clarity.

The observed quadrature squeezing and multipartite entanglement strongly depend on the sideband frequencies involved in their measurements. Excess noise distributions at the sideband could destroy squeezing as well as entanglement at the low sideband frequencies. Moreover, in the presence of the Bragg scattering effect, the true covariance matrix at high sideband frequencies can be far from real-symmetric but Hermitian and cannot be fully captured by homodyne detections³⁸. Figure 3e shows the squeezing levels of the eight eigen-supermodes at broad sideband frequencies, estimated from their measured covariance matrices. Theoretical results modelled by the quantum Langevin equation (2) (with the inclusion of system loss) and experimental results are in good agreement (Fig. 3e), considering the incompleteness of standard homodyne detections⁴⁸. Notable quadrature squeezing greater than 1 dB has been observed across the broad sideband. Furthermore, in Fig. 4d, at different sideband frequencies, we measured the violations of inequalities for different cluster states. The inequalities are successfully violated for all four-qumode cluster states (linear, box and star cluster states) at up to about 200 MHz sideband frequencies, and for the six-qumode linear cluster state at up to about 100 MHz sideband frequencies. These results indicate the robustness of multi-qumode entanglement against low-frequency excess noises, which is substantial for practical implementations.

In summary, we have demonstrated chip-scale deterministic generation of continuous-variable multipartite entanglement in an integrated optical microcomb and verified entanglement by experimental violations of the van Loock–Furusawa criteria. We have measured the full nullifier correlations to characterize multipartite entanglement structures of the generated states, which are closely approximated to the corresponding cluster-type structures^45,46,47. This demonstration was made possible by a thorough exploration of the physical mechanisms underlying multipartite entanglement generation in microcombs, coupled with the coherent integration of advanced polychromatic pumping-detection schemes and technologies^30,31,39,40. Despite working with small-scale entangled states and modest squeezing levels, leveraging the unique capabilities of integrated photonics opens avenues for further scaling and enhancement (see discussions in Supplementary Information section 4). Scaling the number of entangled qumodes to hundreds or thousands can be facilitated by using larger microcomb sizes, using broadband microcombs⁴⁹ or using soliton combs as polychromatic pumps³⁷. Furthermore, multiplexing frequency modes with path and temporal modes in integrated photonics platforms offers a pathway for further increasing the size of entangled states. Dedicated optimizations of the escape efficiency of squeezed beams in ultrahigh-Q microresonators can lead to enhanced squeezing⁵⁰. The scalability and capability of CVIQP technologies could be ultimately unlocked by co-integrating continuous-variable quantum light sources, linear-optic quantum circuits and homodyne detectors⁵¹, as well as DVIQP devices such as single-photon sources and photon-number resolving detectors^6,34. The development of discrete- and continuous-variable hybrid integrated quantum photonics^4,5,52 provides opportunities for deployable chip-scale quantum sensing^3,14, practical quantum networking^2,11 and universal quantum computing^53,54.