Mouse breeding and husbandry
All experimental procedures related to the use of mice were approved by the Institutional Animal Care and Use Committee of the Allen Institute for Brain Science (AIBS) in accordance with NIH guidelines. Mice were housed in rooms with controlled temperature (21–22 °C) and humidity (40–51%) conditions at no more than five adult animals of the same sex per cage. Mice were provided food and water ad libitum and were maintained on a regular 14:10 h light–dark cycle. Mice were maintained on the C57BL/6J (RRID: IMSR_JAX:000664) background. We excluded any mice with anophthalmia or microphthalmia.
The presence of vaginal plugs was monitored at 12-h intervals (6:00 and 18:00). To collect embryos with accuracy to 0.5 days, only dams with visible plugs were used to obtain embryonic time points. For postnatal time points, births were recorded at 12-h intervals (6:00 and 18:00). Animal handling was reduced as much as possible until weaning at P21. At weaning, animals were separated from their mothers and opposite-sex siblings. Weaned mice were group-housed, kept separate from the opposite sex and maintained under normal housing conditions until dissection.
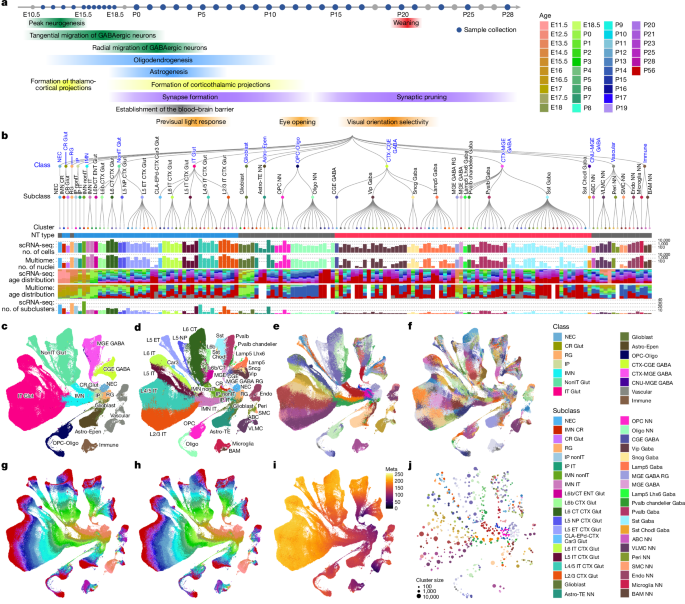
All animals used for data generation are listed in Supplementary Table 1. No statistical methods were used to predetermine sample sizes. In total we used 53 mice to collect scRNA-seq data from 913,297 cells across 35 time points between E11.5 and adulthood: embryonic day E11.5, E12.5, E13.5, E14.5, E15.5, E16.5, E17.0, E17.5, E18.0 and E18.5; postnatal day P0, P1, P2, P3, P4, P5, P6, P7, P8, P9, P10, P11, P12, P13, P14, P15, P16, P17, P19, P20, P21, P23, P25 and P28; and adult stage P54–P68 (collectively simplified as P56). Brain dissections for all groups took place in the morning. From ages E11.5 to E12.5, we collected whole brain tissue, from ages E13.5 to E14.5, we collected the cerebrum and the brainstem, and from other ages we dissected the visual cortex (VIS). Tissue dissection was performed on about 300-µm coronal sections, and the VIS was identified and dissected out using the Allen CCFv3 reference atlas. The adult samples were taken from the ABC–WMB dataset by selecting scRNA-seq libraries with regions of interest (ROIs) of VIS-PTLp or VISp. For snMultiome data generation, we collected data from 331,831 nuclei from 28 mice across 13 time points: E15.5, E16.0, E17.0, E18.0, P0, P2, P4, P5, P8, P9, P11, P14 and P56. At embryonic time points, we dissected the cerebrum and the brainstem and at postnatal time points, we collected either the VIS or the isocortex.
In some cases, transgenic mice were used for fluorescence-positive cell isolation by FACS. To enrich neurons profiled by scRNA-seq, cells were isolated from the pan-neuronal Snap25-IRES2-Cre line (RRID: IMSR_JAX:023525) crossed to the Ai14-tdTomato reporter (RRID: IMSR_JAX:007914) (31 out of 53 mice, Supplementary Table 1).
Single-cell isolation
Single cells were isolated following a cell-isolation protocol developed at the AIBS71. The brain was dissected, submerged in artificial cerebrospinal fluid (ACSF), embedded in 2% agarose and sliced into 350-μm coronal sections on a compresstome (Precisionary Instruments). Block-face images were captured during slicing. ROIs were then microdissected from the slices and dissociated into single cells.
Dissected tissue pieces were digested with 30 U ml–1 papain (Worthington PAP2) in ACSF for 30 min at 30 °C. Owing to the short incubation period in a dry oven, we set the oven temperature to 35 °C to compensate for the indirect heat exchange, with a target solution temperature of 30 °C. Enzymatic digestion was quenched by exchanging the papain solution 3 times with quenching buffer (ACSF with 1% FBS and 0.2% BSA). Samples were incubated on ice for 5 min before trituration. The tissue pieces in the quenching buffer were triturated through a fire-polished pipette with a 600-µm-diameter opening approximately 20 times. The tissue pieces were allowed to settle and the supernatant, which now contained suspended single cells, was transferred to a new tube. Fresh quenching buffer was added to the settled tissue pieces, and trituration and supernatant transfer were repeated using 300 µm and 150 µm fire-polished pipettes. The single-cell suspension was passed through a 70 µm filter into a 15 ml conical tube with 500 µl high-BSA buffer (ACSF with 1% FBS and 1% BSA) at the bottom to help cushion the cells during centrifugation at 100g in a swinging-bucket centrifuge for 10 min. The supernatant was discarded, and the cell pellet was resuspended in the quenching buffer. We collected 547,092 cells without performing FACS. The concentration of the resuspended cells was quantified, and cells were immediately loaded onto a 10x Genomics Chromium controller.
To enrich neurons or live cells in some samples, cells were collected by FACS (BD Aria II running FACSdiva v.8 (RRID: SCR_001456)) using a 130 μm nozzle, following a FACS protocol developed at AIBS72. Cells were prepared for sorting by passing the suspension through a 70 µm filter and adding Hoechst or DAPI (to a final concentration of 2 ng ml–1). The sorting strategy with example images has been previously described72. We collected 30,833 calcein-positive and Hoechst-positive cells, 18,992 Hoechst-positive cells, 13,912 RFP-positive cells and 302,468 RFP-positive and Hoechst-positive cells (Extended Data Fig. 1d, Supplementary Table 1 and Supplementary Fig. 4). Around 30,000 cells were sorted within 10 min into a tube containing 500 µl quenching buffer. Each aliquot of sorted 30,000 cells was gently layered on top of 200 µl high-BSA buffer and immediately centrifuged at 230g for 10 min in a centrifuge with a swinging-bucket rotor (the high-BSA buffer at the bottom of the tube slows down the cells as they reach the bottom, which minimizes cell death). No pellet could be seen with this small number of cells, so we removed the supernatant and left behind 35 µl of buffer, in which we resuspended the cells. Immediate centrifugation and resuspension allowed the cells to be temporarily stored in a high-BSA buffer with minimal ACSF dilution. The resuspended cells were stored at 4 °C until all samples were collected, usually within 30 min. Samples from the same ROI were pooled, the cell concentration quantified and the samples immediately loaded onto a 10x Genomics Chromium controller.
Single-nucleus isolation
Mice were anaesthetized with 2.5–3% isoflurane and transcardially perfused with cold pH 7.4 HEPES buffer containing 110 mM NaCl, 10 mM HEPES, 25 mM glucose, 75 mM sucrose, 7.5 mM MgCl2 and 2.5 mM KCl to remove blood from the brain73. After perfusion, the brain was rapidly dissected, frozen for 2 min in liquid nitrogen vapour and then transferred to −80 °C for long-term storage using a freezing protocol developed at AIBS74.
For VIS dissections, frozen mouse brains were sectioned using a cryostat, with the cryochamber temperature set at −20 °C and the object temperature set at −22 °C. Brains were securely mounted by the cerebellum or by the olfactory region onto cryostat chucks using OCT (Sakura FineTek 4583). Tissue was trimmed at a thickness of 20–50 µm, and once at the desired location, slices with a thickness of 300 µm were generated to dissect out ROIs following the reference atlas. Images were taken while leaving the dissection in the cutout section. Nuclei were isolated using the RAISINs75 method, but with a few modifications as described in a nucleus isolation protocol developed at AIBS76. In brief, excised tissue samples were transferred to a 12-well plate containing CST extraction buffer. Mechanical dissociation was performed by chopping the sample using spring scissors in ice-cold CST buffer for 10 min. The entire volume of the well was then transferred to a 50 ml conical tube while passing through a 100 µm filter and the walls of the tube were washed using ST buffer. Next the suspension was gently transferred to a 15 ml conical tube and centrifuged in a swinging-bucket centrifuge for 5 min at 500 r.c.f. and 4 °C. After centrifugation, the majority of supernatant was discarded, pellets were resuspended in 100 µl 0.1× lysis buffer and incubated for 2 min on ice. After the addition of 1 ml wash buffer, samples were gently filtered using a 20 µm filter and centrifuged as before. After centrifugation, most of the supernatant was discarded, pellets were resuspended in 10 µl chilled nucleus buffer and nuclei were counted to determine the concentration. Nuclei were diluted to a concentration targeting 5,000 nuclei per µl.
cDNA amplification and library construction
For 10x scRNA-seq, the cell suspensions were processed using a Chromium Single Cell 3′ Reagent Kit v.3 (1000075, 10x Genomics)77. We followed the manufacturer’s instructions for cell capture, barcoding, reverse transcription, cDNA amplification and library construction. We loaded 8,876 ± 2,981 cells per port. We targeted a sequencing depth of 120,000 reads per cell; the actual average achieved was 64,719 ± 60,037 reads per cell across 91 libraries (Supplementary Table 1).
For 10x snMultiome processing, we used a Chromium Next GEM Single Cell Multiome ATAC + Gene Expression Reagent Bundle (1000283, 10x Genomics). We followed the manufacturer’s instructions for transposition, nucleus capture, barcoding, reverse transcription, cDNA amplification and library construction78. For the snMultiome libraries, we loaded 9,276 ± 3,883 nuclei per port. For snRNA-seq, we targeted a sequencing depth of 120,000 reads per nucleus. The actual average achieved, for the nuclei included in this study, was 108,297 ± 65,116 reads per nucleus across 35 libraries (Supplementary Table 1). For snATAC-seq, we targeted a sequencing depth of 85,000 reads per nucleus. The actual average achieved, for the nuclei included in this study, was 122,312 ± 74,159 reads per nucleus across 35 libraries.
Sequencing data processing and QC
To remove low-quality cells, we developed a stringent QC process. Cells were first classified into broad cell classes after mapping to our established ABC–WMB Atlas14, and cell quality was assessed on the basis of gene detection, QC score and doublet score. The QC score was calculated by summing the log-transformed expression of a set of genes for which the expression level was significantly decreased in poor-quality cells. Doublets were identified using a modified version of the DoubletFinder algorithm (available in scrattch.hicat; https://github.com/AllenInstitute/scrattch.hicat, v.1.0.9) and removed when the doublet score was >0.3. In prenatal time points, neuronal precursors of non-cortical origin were excluded on the basis of low expression of Foxg1, Emx1 or Emx2. Using different QC scores and gene-count thresholds among different cell classes (Supplementary Table 2), we filtered out 151,945 cells and kept 761,352 cells for 10xv3 scRNA-seq data (Extended Data Fig. 1a,b).
We used a similar strategy to filter low-quality nuclei for the 10x Multiome snRNA-seq dataset. Nuclei were first classified into broad cell classes after mapping to the ABC–WMB Atlas, and cell quality was assessed on the basis of gene detection and the doublet score. For the 10x Multiome snRNA-seq dataset, although the overall gene counts were lower compared with the 10xv3 scRNA-seq dataset, they showed a more distinct bimodal distribution, which enabled us to retain stringent QC criteria (Supplementary Table 2). For 10x Multiome snATAC-seq data, we used the default criteria implemented in ArchR (RRID: SCR_020982)59: the number of unique nuclear fragments (nFrags > 1,000) and signal-to-background ratio (transcription start site (TSS) > 3). For the 10x Multiome dataset, only nuclei that passed both snRNA-seq and snATAC-seq QC criteria (a total of 261,380 nuclei) were included in downstream analyses (Extended Data Fig. 1a,c).
Inferring synchronized developmental age
To estimate the synchronized developmental age for each single cell, we trained k-NN models (Extended Data Fig. 2a). We first performed global de novo clustering for 10xv3 single-cell datasets across all time points using the R package scrattch.bigcat14 (https://github.com/AllenInstitute/scrattch.bigcat). The whole gene-count matrices were chunked to smaller parquet files that could be loaded efficiently and concurrently using the arrow package (v.12.0.1; https://github.com/apache/arrow/ and https://arrow.apache.org/docs/r/). The automatic iterative clustering method iter_clust_big was used with stringent differential gene expression criteria as described in a previous study12: q1.th = 0.5, q.diff.th = 0.7, de.score.th = 150, min.cells = 50. We then performed principal component analysis (PCA) based on the gene expression matrix of 5,824 marker genes derived from the de novo clusters. We downsampled up to 200 cells per cluster to avoid memory limitations. The principal components (PCs) based on the sampled cells were then projected to the entire datasets. We selected the top 100 PCs and removed 1 PC with more than 0.7 correlation with the technical bias vector, defined as log2[gene count] for each cell. The k-NN algorithm identified 10 nearest neighbours to each of the single cells in the input data based on their distances computed using the selected 99 PCs. The inference of synchronized developmental age using the k-NN algorithm was iteratively run: in the first iteration, each cell was assigned a predicted age on the basis of the most common age among its ten neighbours. In subsequent iterations, the predicted age of each cell was assigned on the basis of the most common predicted age from the previous iteration of its ten neighbours. Ten iterations were run until convergence into the final synchronized ages (Fig. 1h and Extended Data Fig. 2a,d).
Label transfer and clustering
For adult cells (P56), cell-type identities were assigned by mapping to the ABC–WMB Atlas14 using the R package scrattch.mapping (v.0.55; https://github.com/AllenInstitute/scrattch.mapping)79. Mapped clusters were merged on the basis of DE criteria to define final cluster identities. For earlier developmental ages (P0–P28), cell types were assigned using Seurat80 (RRID: SCR_016341) with the reciprocal PCA (RPCA) label transfer approach (Extended Data Fig. 2b). Specifically, cell-type labels were transferred from the P56 reference to P20–P28, and from P20–P28 to P17–P19, and so forth. Clusters with fewer than ten cells in an age bin were reassigned to the nearest cluster using the k-NN approach (k = 10). After cell-type assignment, additional iterative clustering was performed in each cluster and synchronized age bin to identify subclusters (Extended Data Fig. 2a).
For global clusters that were dominantly from the embryonic stage (E11.5–E18.5), we used scrattch.mapping to assign cell types on the basis of previously published data31, a mouse development study that covered E7–E18 using a list of 2,947 marker genes derived from the study’s cluster-specific markers. Global clusters that were mapped to RG were assigned as a NEC subclass (dominated by cells from E11.5 to E12.5 and expressing Hmga2) or RG (dominated by cells from E13.5 to E16.5 and expressing Sox2, Pax6, Hes1 and Hes5). Neurons born early at E11.5 and E12.5, characterized by enrichment in Reln, Trp73 and Calb2, were classified as a CR Glut subclass. According to the trajectory analysis, clusters at E11.5 and E12.5 that were enriched in Crabp2, Ebf2 and Eomes, and which give rise to CR Glut, were categorized as the IMN CR subclass. Global clusters mapped to neuronal IPs were identified as the IP class (with high expression of Eomes, Btg2, Neurog2 and Gadd45g). IP clusters enriched in Neurog1, Lhx9, Rmst and Nhlh1 were classified as the IP nonIT subclass, whereas those with higher levels of Pou3f2, Lama2 and Slco1c1 were classified as the IP IT subclass. Embryonic global clusters that were highly enriched in the neuronal markers Dcx, Neurod1, Neurod2, Neurod6, Tubb3 and Tbr1 were annotated as the IMN class. In the IMN class, clusters enriched in Fezf2 were labelled as the IMN nonIT subclass, whereas those enriched in Pou3f2 were labelled as the IMN IT subclass. We also defined the glioblast subclass (which expresses Tnc, Fabp7, Qk, Lipg and Slco1c1). Cells in each embryonic subclass were merged into one or a few clusters, followed by iterative clustering in each cluster and each synchronized age bin to identify subclusters. Finally, we merged the subclusters in each cluster that did not pass the DE gene criteria: q1.th = 0.4, q.diff.th = 0.7, de.score.th = 150, min.cells = 10.
The final developmental cell-type taxonomy with annotations at the class, subclass, cluster and subcluster levels is summarized in Supplementary Table 3.
Differential gene expression analysis and marker selection
We performed differential gene expression analysis both at the clustering step for each iteration and after clustering between all pairs of subclusters (or global clusters). We applied the limma package (implemented in scrattch.bigcat package) to perform this analysis. For each pairwise comparison, we computed DE genes (padj.th = 0.01, q1.th = 0.4, q.diff.th = 0.7, de.score.th = 150, and log2[FC] ≥ 1.5). We selected the top 15 DE genes in each direction and pooled such genes from all pairwise comparisons. All DE genes are shown in Supplementary Table 4.
Reconstruction of the developmental trajectory
Popular computational methods such as Monocle81, PAGA82, Slingshot83 and RNA Velocity84 leverage the gradients in the transcriptomic space to infer a cell-type trajectory. However, a primary challenge that these tools face is the deconvolution of the temporal gradient from other gradients associated with cell-type heterogeneity. We found that these tools were not able to derive the trajectory of cortical development with the desired cell-type resolution. For example, the trajectories inferred by Monocle3 (ref. 40) switched back and forth between different layers and different ages for IT cells (Extended Data Fig. 2c), which made the results difficult to interpret.
Given the cell-type identities at the adult stage and the dense temporal sampling, we were able to progressively propagate cell-type identities between two adjacent ages (see above). As all cells in the later age evolve from cells in the earlier age, we found that identifying corresponding cell types in two adjacent time points that have only subtle transcriptomic differences could be readily solved using existing methods such as Seurat label transfer. Here instead of using actual age, we used synchronized age to derive trajectories for clusters with adult cell-type labels. This strategy worked well until earlier developmental time points, when cells develop more rapidly and cells in the same age can be present in different developmental states. During this period, when cells mainly belong to the RG, IP, IMN or glioblast classes, the transcriptomic gradient corresponding to differentiation is dominant, whereas cell-type diversity is much lower compared to later ages. We found that established methods such as Monocle3 worked well in this case. Therefore, we defined the embryonic trajectory using the same k-NN approach but using Monocle3-based pseudotime instead of synchronized age.
For postnatal stages, we connected each cluster in a synchronized age bin with its most likely antecedent in the previous bin using the k-NN approach (Extended Data Fig. 2b). Cells from two consecutive synchronized age bins were integrated using the Seurat RPCA approach. To assign edge weights between clusters from adjacent age bins, we applied a bootstrapping strategy: for cells of each cluster in the later age bin, we identified their 50 closest neighbour cells from the earlier age bin in the integrated latent space and then calculated the proportion belonging to each candidate antecedent cluster. Clusters with fewer than ten cells in a given age bin during label transfer were reassigned, and in such cases, we identified their nearest neighbours from the current and all preceding age bins in the global PCA space. We repeated these steps 100 times with a subsampling of 90% of cells, and median proportions were used as edge weights. Edge weights of >0.2 were retained and shown in Supplementary Table 5, and we chose the edge with maximal weight for each cluster for the resulting trajectory (Supplementary Table 5).
For the embryonic stages, cells are changing substantially in the same age. We used the above strategy in pseudotime that was computed using Monocle3 (ref. 40) (Extended Data Fig. 2c). For cells in each cluster, we identified their 50 closest neighbour cells from clusters at an earlier median pseudotime using a bootstrapping strategy. Same as for the postnatal stages, edge weights of <0.2 were removed. The developmental trajectory across the entire timeline from E11.5 to P56 is summarized in Supplementary Table 5 (Figs. 2a and 3).
Comparison of Seurat RPCA and scVI integration
To assess the robustness and consistency of our developmental cell-type taxonomy, we compared the integration results from two different methods: Seurat RPCA and scVI (Supplementary Fig. 1). We applied both methods to integrate the scRNA-seq data from adjacent age bins (P0–P56) with age as a batch effect. For scVI, we used three sets of highly variable genes (HVGs; 1,000, 2,000 and 3,000 genes) between adjacent age bins. For Seurat RPCA, we performed data integration using the parameters nfeatures = 2,000, dims = 1:30, k.anchor = 50 and k.weight = 100. For scVI, we tested three model architectures with varying complexity: default (n_hidden = 128, n_layer = 1, n_latent = 10); medium (n_hidden = 128, n_layer = 2, n_latent = 32); and large (n_hidden = 256, n_layer = 3, n_latent = 32). This resulted in a total of nine scVI model settings. Both Seurat RPCA and scVI produced highly consistent results, with small differences observed between the two methods. The integration facilitated alignment of the cell-type annotations across adjacent age bins, which further confirmed the robustness of the taxonomy. The slight variations among the nine scVI models were mainly attributed to the differences in model complexity and the number of HVGs, with more HVGs demonstrating a slightly higher resolution in capturing subtle transcriptional changes between cell types. Moreover, Seurat RPCA was able to capture rare cell types, for example, Sst Chodl. Both methods were able to reliably recover the majority of developmental transitions and cellular heterogeneity.
Pseudotime
We computed the overall pseudotime in the global PCA space (Fig. 1i) using the entire developmental trajectory described above separately for the three independent trajectories: excitatory neurons and glia derived from NECs; MGE GABAergic neurons derived from MGE GABA RG; and CGE GABAergic neurons starting at CGE GABA. Each node of the trajectory was a cluster-by-synchronized-age-bin group of cells. The node centroid was defined as the median of all the corresponding cells in each PCA dimension. Pseudotime was computed iteratively over ten independent runs. In each iteration, one random cell in the starting node of each trajectory was set at pseudotime = 0. For each cell in the starting node, the pseudotime was the Euclidean distance to the randomly selected cell in the global PCA space. The Euclidean distance of the starting node centroid to the randomly selected cell was also computed. For each of the subsequent nodes, we computed the cumulative Euclidean distance to the starting cluster by summing the edge lengths along the trajectory, where each edge was defined as the distance between consecutive node centroids in the global PCA space. The pseudotime of each cell in each subsequent node was computed as the sum of the following parameters: (1) the distance from the cell to its closest antecedent node centroid; (2) the closest cumulative Euclidean distance of the antecedent node to the starting node; and (3) the distance from the starting node to the randomly selected cell. Finally, we took the mean of the pseudotime for each cell computed from the ten independent runs.
Clustering temporal gene expression trajectories
To capture dynamic changes of each gene in each subclass over developmental time, we identified major temporal patterns using an unsupervised clustering approach. First, to identify cell-type-specific and temporal-specific marker genes, we computed pairwise DE genes between subclasses in each synchronized age and between synchronized ages in each subclass. We then computed the average expression of each marker gene identified above for each subclass-by-age group and normalized the values, with a maximum value of 1 for each gene across all subclass-by-age groups. To extend the analysis to prenatal time points, we also included cells from the antecedent clusters that give rise to the given postnatal subclass. Afterwards, we fit the normalized expression trajectory of each gene in each subclass using a generalized additive model with synchronized age as the predictor. The model, implemented using the ‘gam’ function from the R package mgcv85, used cubic regression splines (bs = “cr”), with a basis dimension of 12 (k = 12) to capture gradual temporal changes without overfitting. To optimize smoothing estimates, we used the restricted maximum likelihood method, which provides robust and accurate performance in noisy and complex datasets. The fitted gene trends were hierarchically clustered using the R package fastcluster86 with a Ward linkage and Euclidean distance metric. The hierarchical tree was cut at a height of 10 using the ‘cutree’ function, resulting in 394 clusters. The clusters were further merged using k-means, which resulted in 36 distinct gene trajectory patterns (Fig. 4).
Assessing cell-type predictive power of adult marker genes across developmental ages
We performed fivefold cross-validation to classify subclasses at each individual postnatal age using different sets of marker genes derived from adult VIS subclasses: all 1,035 marker genes, 71 TF marker genes, 139 functional genes (including neuropeptides, GPCRs, ion channels and transporters) and 183 genes coding for adhesion molecules. We used the ‘map_cells_knn_big’ function in the scrattch.bigcat package, the same method implemented in scrattch.mapping79, to perform the cross-validation.
Quantification of DE genes along developmental trajectory
To quantify the developmental rate of each subclass, we computed the sum of log fold changes of DE genes (|log2FC| > 1, Benjamini–Hochberg adjusted P < 0.05) between each pair of adjacent synchronized ages, separately for DE genes with positive or negative changes (Fig. 5b). To control differences in sample sizes (that is, number of cells per age), we used a sliding window approach with a bandwidth of 2. Specifically, for a given comparison (for example, P1 versus P2), we compared combined samples from adjacent time points (for example, P0 + P1 versus P2 + P3). For each group in the comparison, we sampled up to 500 cells (for example, up to 1,000 cells for P0 + P1; Supplementary Table 3). To assess uncertainty and account for sampling variability, we randomly subsampled 70% of the selected cells and repeated the DE analysis 100 times. This enabled us to estimate the variability and mean in log2[FC] and provided more robust measures of developmental rate across subclasses.
P0 MERFISH data generation
Brain dissection and freezing
Mice were transferred from the vivarium to the procedure room with efforts to minimize stress during transfer. Mice were anaesthetized with 0.5% isoflurane. Brains were rapidly dissected and selected on the basis of the absence of dissection damage. The selected brain was flash-frozen in OCT using 2-methylbutane chilled with liquid nitrogen and stored at −80 °C.
Cryosectioning
The freshly frozen brain was sectioned at 14 µm using Leica 3050 S cryostats. The OCT block was trimmed in the cryostat until the desired starting section was reached. Sections were collected every 100 µm to evenly sample the brain from posterior to anterior. Each section was mounted onto a functionalized 20-mm coverslip treated with yellow–green fluorescent microspheres (Vizgen, 2040003).
Probe design
A 500-gene panel was designed as previously described14. In brief, we chose the in-house P0 whole brain transcriptomic taxonomy (unpublished observations) as the reference and excluded any genes that had shown poor performance in previous MERFISH experiments. Starting with a default set of well-established marker genes curated from previous studies, we expanded the panel by selecting additional genes to ensure that there are at least two DE genes in both directions for each pair of clusters, using the ‘select_N_markers’ function from the scrattch.bigcat package, and selected the top 350 genes (including the default genes) from this list.
To evaluate performance, we conducted 5-fold cross-validation using these 350 genes using scrattch.bigcat package as described above. For clusters with cross-validation accuracy values below 0.7, we further refined the panel by selecting one additional DE gene in each direction using the same function. Our goal was to build a solid gene panel with strong predictive power at the subclass level and be opportunistic at resolving finer cell types. Except for the default gene set, the remaining genes were largely ordered with decreasing predictive power. We submitted a total of 729 genes to the Vizgen portal and selected the top 500 genes that passed the additional filters applied by Vizgen. The final gene set provided an overall cross-validation accuracy of 85.1% at cluster level and 98.0% at subclass level.
Fixation and dehydration
After air drying on the coverslips for 10–15 min, the tissue sections were loaded into a Leica Autostainer XL (Leica ST5010). They were washed in 1× PBS for 1 min, fixed in 4% paraformaldehyde for 15 min, washed in 1× PBS for 5 min 3 times, washed in 70% ethanol and then stored in 70% ethanol at 4 °C. They were stored for at least 1 day and no more than 6 weeks before subsequent analyses .
Hybridization
For staining the tissue with MERFISH probes, a modified version of instructions provided by the manufacturer was used. All solutions were prepared according to the instructions provided by the manufacturer. For hybridization, samples were removed from the 70% ethanol and washed in a Petri dish containing Vizgen sample prep buffer (Vizgen, 20300001). Sample prep buffer was aspirated, and the samples were equilibrated with 5 ml Vizgen formamide wash buffer (Vizgen, 20300002) in a humidified incubator at 37 °C for 30 min. Formamide wash buffer was removed by aspiration and a 50 μl droplet of MERSCOPE Gene Panel Mix was added onto the centre of the tissue section. Next, the tissue section was covered with Parafilm and stored in a humidified 37 °C cell culture incubator for 36 h.
Gel embedding
Parafilm covering the sections was removed, and 5 ml of the Vizgen formamide wash buffer was immediately added. Sections were incubated at 47 °C for 30 min. Formamide wash buffer was aspirated and the previous step repeated. Sections were washed with Vizgen sample prep wash buffer after the second formamide wash for 2 min. Next, 110 µl Vizgen gel embedding solution (Vizgen 20300004) with APS and TEMED was added onto the centre of a Gel Slick-coated XL microscope slide (Ted Pella, 260231) and any excess embedding solution was gently removed. To enable the gel to fully polymerize, the sections were incubated at room temperature for 1.5 h. To clear the tissue, the section was incubated in 5 ml Vizgen Clearing solution (Vizgen 20300003) with proteinase K (NEB P8107S) according to the manufacturer’s instructions for at least 16–18 h in a humidified incubation oven at 37 °C.
Imaging
Following clearing, sections were washed twice for 5 min in sample prep wash buffer (Vizgen, 20300001). Vizgen DAPI and PolyT stain (Vizgen, 20300021) was applied to each section for 15 min followed by a 10 min wash in formamide wash buffer. Formamide wash buffer was removed and replaced with sample prep wash buffer during MERSCOPE set up. Next, 100 µl RNase inhibitor (New England BioLabs M0314L) was added to 250 µl imaging buffer activator (Vizgen, 203000015) and this mixture was added through the cartridge activation port to a pre-thawed and mixed MERSCOPE Imaging cartridge (Vizgen, 1040004). Fifteen millilitres of mineral oil (Millipore-Sigma m5904-6X500ML) was added to the activation port, and the MERSCOPE fluidics system was primed according to Vizgen instructions. The flow chamber was assembled with the hybridized and cleared section coverslip according to Vizgen specifications, and the imaging session was initiated after collection of a 10× mosaic DAPI image and selection of the imaging area. For specimens that passed the minimum count threshold, imaging was initiated, and processing was completed according to Vizgen’s proprietary protocol.
MERFISH data analysis
Raw MERSCOPE data were decoded using Vizgen software (v.231). For cell segmentation, we used an in-house model to segment cells by applying the human-in-the-loop approach introduced in Cellpose (v.2.0)87. Starting with the ‘cyto2’ pretrained model in Cellpose, we trained our own model using the Cellpose GUI with the human-in-the-loop method, in which model predictions were iteratively corrected by the user and incorporated into training. Our model was trained on 24 two-channel images (200 × 200 µm) that represented a range of cellular densities, developmental stages and both sexes.
We used DAPI as the nuclear channel. For the cytoplasmic channel, we generated a post hoc stain from the measured mRNA transcripts. Transcripts were binned into a 2D histogram aligned with the DAPI channel, convolved with a Gaussian filter (σ_z = 1, σ_x/y = 3) and processed with a 3D median filter (z = 2, x/y = 10). This produced a stain-like signal that improved cytoplasmic boundary detection. Segmentation was performed in 3D using Cellpose’s volumetric mode, which computes flows across the yx, zx and zy planes and averages them before running 3D dynamics.
MERFISH QC metrics
To ensure high quality in our P0 MERFISH dataset, we retained cells that met the following criteria: at least 6 detected genes and at least 30 detected mRNA transcripts. We also used the percentage of blank barcodes per cell as a marker for low-quality cells. Blank barcodes do not encode for any gene targeted by the panel and thus represent a measure of false-positive detection. We excluded cells with a blank barcode percentage greater than 2%. Next, we applied the Solo algorithm to identify doublets88 independently on each section. Solo outputs a probability score for each cell being a singlet or doublet. We computed the difference (dif) between singlet and doublet scores of the predicted doublets. To define a threshold for doublet classification, we calculated the 0.9 and 0.1 quantiles of the dif distribution among the predicted doublets. The threshold was set as q0.9(dif) − q0.1(dif), and all cells with dif values above this threshold were classified as doublets. These cells were excluded from the dataset.
Spatial mapping of developmental VIS cell types at P0
To identify spatial distribution of cell types at P0, we used the unpublished P0 whole brain scRNA-seq taxonomy (P0 WB) as a reference to bridge the P0 whole brain MERFISH dataset. First, we mapped the MERFISH dataset to P0 WB using the scrattch.mapping79 package based on the 500 gene panel. In parallel, cells from E18.5, P0 and P1 in this study (referred to as P0 VIS) were also mapped to P0 WB using a combined marker set from both datasets. E18.5 and P1 cells were included to increase cell numbers, as their transcriptomic differences from P0 were minor. We selected P0 WB clusters to which P0 VIS clusters were mapped and then extracted MERFISH cells mapped to those clusters with mapping scores of ≥0.5. These MERFISH cells were then directly mapped to the P0 VIS reference. Owing to substantial transcriptomic heterogeneity in IMN types and a gradual continuum between IMN and IP populations, we first integrated selected MERFISH and P0 VIS reference cells labelled as IMN and IP using scVI34 (n_hidden = 256, n_layer = 3, n_latent = 32), and trained a random forest classifier on the scRNA-seq clusters. Then we performed flat mapping with bootstrapping, randomly sampling 80% of the genes in each of 100 iterations. This enabled subcluster-level mapping of MERFISH cells, which improved cell-type resolution and provided reliable confidence estimates essential for distinguishing closely related cell types.
Identification of gene modules
Synchronized age-associated co-regulated genes specific to each subclass or class were determined using an unsupervised clustering approach. First, we computed pairwise DE genes (padj.th = 0.01, q1.th = 0.5, q.diff.th = 0.7, de.score.th = 150, and log2[FC] ≥ 1.5) between subclasses or classes in each synchronized age bin or across synchronized age bins in each subclass or class. We selected the top 15 DE genes in each direction and pooled such genes from all pairwise comparisons. We then computed the average expression of each DE gene among cells in each subcluster. We computed for each gene the k-NN (k = 5) using cosine similarity metrics, then computed the Jaccard similarity graph based on the number of shared nearest neighbours between every pair of genes. The Louvain clustering algorithm (resolution = 2) based on the Jaccard graph was used to identify gene co-expression modules. All the gene modules are summarized in Supplementary Table 6.
GO enrichment analysis
To relate various gene modules to known biological processes, we performed gene set enrichment analyses using the R package clusterProfiler 4.0 (RRID: SCR_016884)89 and g:Profiler (RRID:SCR_006809)90. The function ‘gconvert’ from gProfiler2 (RRID:SCR_018190) was used to convert gene identifiers to their Ensembl identifiers. The functions ‘enrichGO’ and ‘simplify’ from clusterProfiler were then used to enrich GO terms from all three GO databases (Molecular Function, Biological Process and Cellular Component). A Benjamini–Hochberg adjusted P value cut-off of 0.01 was used to determine significant GO terms.
Integration of snMultiome and scRNA-seq datasets and label transfer
We performed global de novo clustering of the Multiome snRNA-seq dataset following nucleus-level QC (gene count ≥ 1,000, TSS enrichment ≥ 3, nFrags ≥ 1,000 and doublet score ≤ 0.3). Clusters outside the cortex were removed on the basis of low expression of the dorsal forebrain markers Foxg1, Emx1 and Emx2 (Supplementary Table 2). To further identify and remove non-cortical clusters at early developmental ages, we applied the same MERFISH mapping strategy described above, using the P0 whole brain taxonomy as a bridge. Specifically, selected P0 MERFISH cells were mapped to P0 snMultiome clusters through shared P0 whole brain clusters, which enabled the identification and removal of additional non-cortical snMultiome clusters. For assigning identities of snMultiome nuclei, we mapped their transcriptomes to the scRNA-seq developmental cell-type taxonomy. We integrated scRNA-seq data (subsampled up to 200 cells per cluster) and Multiome snRNA-seq data (all nuclei) using scVI34 (n_hidden = 512, n_layer = 4, n_latent = 50) using a combined set of DE genes based on the scRNA-seq subclusters and snMultiome global clusters (Supplementary Table 4). In the integrated latent space, we applied a random forest classifier to predict each nucleus’ most probable cell-type identity, using the scRNA-seq taxonomy as a reference. For this, we used the RandomForestClassifier implementation from the sklearn.ensemble module in Python, with default parameters except for n_estimators = 100. Last, we performed further annotation and QC of each predicted cluster and filtered out a small set of clusters deemed to be low quality or outside the cortex based on additional mapping to the adult ABC–WMB atlas, which resulted in a final set of 200,061 Multiome nuclei for further analysis. The final Multiome snRNA-seq to scRNA-seq developmental cell-type taxonomy mapping result is shown in Supplementary Table 8 (Figs. 1b and 6a–d).
Multiome peak calling
To call chromatin accessibility peaks in the snATAC–seq data, we first categorized snMultiome cells (nuclei) according to both subclass and age group. To accumulate enough samples with sufficient statistical power for comparative analysis, we combined consecutive ages into the following groups: E13–E16.5, E17–E18.5, P0–P3, P4–P6, P7–P10, P11–P15 and P56, which are broadly consistent with the synchronized age bins (Extended Data Fig. 2d). We kept only the subclass-by-age groups with more than 50 nuclei. We generated pseudobulk replicates using the ArchR59 function ‘addGroupCoverages’. We created a reproducible merged peak set using function ‘addReproduciblePeakSet’. Finally, we built the peak-by-cell matrix, which contains insertion counts in the merged peak set, using function ‘addPeakMatrix’.
Identification of DA peaks
To identify DA peaks, as the peak presence in each cell is mostly binary, we chose the Chi-squared test to evaluate the significance of DA peaks across all 882,075 peaks identified above between every pair of subclass-by-age groups. In addition to the log2[FC] and adjusted P value (adj.P) based on the Chi-squared test, we also computed the fraction of cells in each category with non-zero counts for each peak. To choose significant DA peaks, we required log2[FC] > 1, adj.P < 0.05 and fraction of cells with non-zero value in the foreground category to be >0.05. This method was implemented in ‘de_all_pairs’ function in the scrattch.bigcat package with extensive parallelization for efficiency. Because of the extensive diversity in cell types overall, we opted for pairwise comparisons instead of one-versus-all comparisons. This decision was made because the cell types in the background group exhibit high heterogeneity in one-versus-all comparison scenarios, which poses challenges in detecting subtle differences. The all-pairwise approach offers enhanced accuracy in identifying DA peaks across both similar and dissimilar pairs of cell categories.
Identification of peak modules with similar cell-type and temporal specificity
To identify peaks that regulate different cell types at different developmental ages, we first extracted the DA peaks for each age group across different subclasses. We then pooled all the DA peaks identified between different subclasses across all age groups and clustered them to identify peak modules. To do so, we first computed the peak-by-category matrix as the average number of reads in each peak per subclass-by-age group, divided by the total number of reads across all peaks per subclass-by-age group, then multiplied by 30,000. The clustering was performed on peak-by-category matrix, subset to the DA peaks, using the Jaccard–Leiden clustering algorithm. We first computed for each peak the k-NN (k = 10) using cosine similarity metrics, then computed the Jaccard similarity graph based on the number of shared nearest neighbours between every pair of peaks, and finally performed the Leiden clustering algorithm based on the Jaccard graph. In most cases, we used resolution index = 2. In cases when we observed more heterogeneity in the peak module, we increased the resolution index accordingly. This method is robust, efficient and scalable, and generates peak modules with high cell-type and temporal specificity.
Identification of peak–gene pairs with matching accessibility and gene expression
We first extracted all the peak and gene pairs such that the gene is located within the 5 Mb window centred at the peak. Then we computed the correlation between the average peak accessibility and average gene expression based on the Multiome dataset across subclass-by-age groups. Given that a gene can be regulated by different peaks in different cell types and/or different ages, the correlation is computed only in different subsets in different contexts, for example, in IT subclasses only. We chose a minimal correlation of 0.5 to select such peak–gene pairs. Furthermore, we computed the average accessibility profile across subclass-by-age groups for all the peaks in each peak module. Subsequently, we calculated the correlation between the average expression in each subclass-by-age group of each gene and the peak module average profile described above. We then filtered and retained only those peak–gene pairs if the gene has the strongest correlation with the peak module corresponding to the respective peak. To accommodate space constraints, for each peak module, only the top 500 selected peak–gene pairs with the strongest peak–gene correlations were included for visualization (Supplementary Table 9).
Differential motif analysis
We first scanned all the peak sequences using motif database with ArchR ‘addMotifAnnotation’ function, which produced a matrix that included the number of motif occurrences in each peak. We used JASPAR 2024 CORE non-redundant motif database (https://jaspar.elixir.no/downloads/), which enabled us to associate each motif to a corresponding TF. To perform differential motif analysis on peaks in different modules, we again used Chi-squared tests between all pairs of modules using ‘de_all_pairs’ function, using cutoff log2[FC] > 2, adj.P < 0.05, and fraction of peaks with non-zero motif occurrences in the foreground of >0.1. The absolute log2 odds against random chance considering all the peaks should also be >1. Once more, we conducted pairwise comparison across all peak modules, as we did not have sufficient previous knowledge of which peak modules might share common or distinct motifs. This strategy enabled us to identify enriched motifs in different combinations of peak modules. When multiple similar motifs were identified, we chose to report the ones associated with stronger regulators based on the GRN analysis described below.
Inference of gene regulatory networks
Using SCENIC+ (ref. 60), we identified triplets consisting of a TF, a target peak and a target gene that met the following criteria: (1) TF expression should predict target gene expression; (2) the peak lies within 150 kb of the TSS of the target gene or in its gene body; (3) peak accessibility should predict target gene expression; (4) the peak contains the TF-binding motif; and (5) the TF motif should be enriched in the peak module to which the peak belongs. The choice of 150 kb to target the TSS was adopted from SCENIC+. We aimed to identify both activating and repressing TF interactions. For activation, we required that the TF positively correlates with both the accessibility of the target peak and the expression of the target gene and is expressed at the time of peak or gene activation in the same cell type. For repression, we required a negative correlation between the TF and both peak accessibility and gene expression, and to be expressed at or before the activation of the peak or gene, although not necessarily in the same cell type. As anticorrelation alone does not confirm repression, owing to potential motif matches by chance, or binding by other TFs from the same family, we further limited candidate repressors to TFs with known repressive functions from the literature. Each triplet was assigned a confidence score, and only the top-ranked predictions are presented (Supplementary Table 10).
Building on the SCENIC+ framework60, we integrated Multiome data (snRNA-seq and snATAC-seq) with motif analysis to identify regulatory relationships through triplet scores that link TFs, accessible chromatin peaks and target genes. We reimplemented the core concepts of SCENIC+ with modifications tailored to developmental datasets and to enable better integration with the ArchR pipeline. This approach enabled us to use a consistent pre-processed dataset while flexibly applying regulatory network analysis across distinct trajectories to capture cell-type specific TF–target interactions in context rather than assuming static relationships across the entire dataset.
The key steps of triplet score computation are outlined in Extended Data Fig. 13a. We began by selecting candidate TFs that are associated with differential motifs and exhibit significant differential expression in the trajectory of interest (using counts per million (CPM) as a measure of gene expression level, with maximum log2[CPM] difference of >2.5 across subclasses and age groups). Target genes were filtered to include only the top ten DE genes (|log2[FC]| > 2) from all subclass and age group pairwise comparisons in the trajectory. For each target gene, triplets were computed by scoring all relevant TFs and their associated accessible peaks, which resulted in a final score that reflects the confidence of each TF–peak–gene interaction.
Following the SCENIC+ approach, we inferred TF-to-gene relationships by combining XGBoost-based prediction of TF influence on gene expression. We retained interactions with importance gain of >0.01 and absolute correlation of >0.05. Gene–gene correlations were computed at the single-cell level using imputed values averaged from the 20 nearest neighbours in the scVI latent space, which provides greater robustness than raw expression values. However, for the XGBoost model, we used raw log2[CPM] data, as such data better highlight distinct marker genes and produce more interpretable results.
To infer peak-to-gene relationships, we also used the XGBoost model to predict target gene expression using all the peaks within 150 kb of the TSS or in the gene body. Owing to sparsity of the snATAC–seq data, imputed values were used to fit the model. We filtered the interactions using the same importance and correlation criteria described above. We filtered the peaks based on the occurrence of TF motif and enrichment of the TF motif in the corresponding peak module. We also computed a TF and peak correlation based on imputed TF expression and peak accessibility. The final score was computed as follows: Triplet score = abs(TF target gain × TF target correlation × peak target gain × peak target correlation × TF peak correlation).
Finally, we considered the timing of TF and target gene expression. To infer a regulatory relationship, the TF must be expressed when the target is activated. We focused on the subclass where the target reaches peak expression and confirmed that the TF is already active in that context. For repressive interactions, for which TF and target expression are anticorrelated, we still required the TF to be expressed before target activation, although not necessarily in the same subclass.
Triplets with scores <10−5 were filtered out. For activating interactions, we required a TF–target correlation of >0.1, a peak–target correlation of >0.05 and a TF–peak correlation of >0.05. For repressive interactions, we required a TF–target correlation of <−0.3, a peak–target correlation of >0.05 and a TF–peak correlation of <−0.1. Activation and repression scores were aggregated across peaks to produce a single interaction score per TF–target pair, and all TF–target pairs were normalized between 0 and 1. Each gene’s network weight was calculated as the sum of its interaction scores, and only nodes with weights > 1 were visualized. Top TFs in each family were selected on the basis of the node weights. These empirical thresholds were chosen to emphasize strong interactions and to reduce network complexity, but they may need to be re-examined in future work.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.